Šíření zvuku v uzavřeném prostoru – difúzní zvukové pole
V uzavřeném prostoru (v místnosti) dochází k odrazu akustické energie od stěn, stropu a podlahy zpět směrem ke zdroji. To má za následek zvýšení hladiny akustického tlaku v porovnání se stavem, který by vznikl ve volném prostoru. Významnou roli zde hraje pohltivost zvuku povrchů, které ohraničují uzavřený prostor.
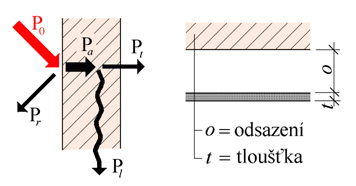
Obr. 18: Distribuce akustického výkonu po dopadu zvuku na stěnu a vysvětlení pojmů tloušťka a odsazení zvuk pohlcujícího obkladu
Při dopadu zvuku o akustickém výkonu P0 [W] na překážku se část tohoto výkonu Pr [W] odrazí a část Pa [W] pohltí. Pohlcený výkon se pak rozdělí na část výkonu Pl [W], která se ztratí (je odvedena konstrukcí mimo sledované místo nebo se promění v jiný druh energie) a na část Pt [W], která projde stěnou a je vyzářena do vedlejšího prostoru. Lze definovat činitele odrazu ![]() , činitele pohltivosti
, činitele pohltivosti ![]() a činitele prostupu (průzvučnosti)
a činitele prostupu (průzvučnosti) ![]() . Tito tři činitelé jsou bezrozměrná čísla, která mohou nabývat hodnot od nuly do jedné.
. Tito tři činitelé jsou bezrozměrná čísla, která mohou nabývat hodnot od nuly do jedné.
Zvuková pohltivost Ai [m2] povrchu konstrukce (i-tého povrchu) je dána součinem plochy povrchu Si [m2] a činitele pohltivosti αi [-]. Celková zvuková pohltivost místnosti A [m2] je součtem zvukové pohltivosti všech ploch, které místnost ohraničují, případně též zvukové pohltivosti předmětů a osob, které se v místnosti nacházejí. Je nutno poznamenat, že činitel pohltivosti α [-] a tudíž i pohltivost A [m2] jsou veličiny závislé na kmitočtu zvuku, a proto všechny jevy související se zvukovou pohltivostí je nutno sledovat a počítat v jednotlivých kmitočtových pásmech obvykle oktávových. Pohltivost zvuku nezávisí jen na materiálu obkladu a jeho tloušťce, ale i na odsazení (tloušťce vzduchové mezery) od tvrdého povrchu stropu nebo stěny.
V bezprostředním okolí zdroje se nachází pole přímých vln. Pokles hladiny akustického tlaku se vzdáleností zde podléhá stejným zákonitostem jako ve volném prostoru a příjemce je schopen sluchem rozpoznat směr, odkud zvuk přichází. Pole přímých vln je omezeno vzdáleností rk [m], která se nazývá dozvuková vzdálenost. Ve vzdálenějších místech uzavřeného prostoru se nachází pole odražených vln, kde převládá akustické vlnění, které do uvažovaného místa dospěje po vícenásobném odrazu od ohraničujících ploch místnosti. Hodnota hladiny akustického tlaku v poli odražených vln je nezávislá na vzdálenosti od zdroje a je určena celkovou zvukovou pohltivostí místnosti A [m2]. V poli odražených vln se předpokládá difúzní charakter zvukového pole.
Představa difúzního zvukového pole je zjednodušeným modelem skutečných podmínek šíření zvuku v uzavřených prostorech, jejichž difúznost je ve skutečnosti vždy do jisté míry narušena. Toto zjednodušení zpravidla umožní dostatečně přesně výpočtem stanovit zatížení uživatelů budov hlukem, ale při sledování kvality zvuku v auditoriích (divadla, kina, koncertní sály, přednáškové síně apod.) je nutný podrobnější popis zvukového pole, kterým se zabývá prostorová akustika.
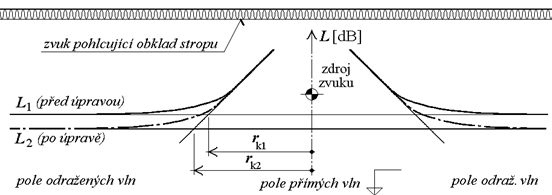
Obr. 19: K vysvětlení pojmu pole přímých vln a pole odražených vln
Na obr. 19 je schéma řezu uzavřeným prostorem (místností) se zdrojem zvuku uprostřed. Formou pravoúhlého diagramu je naznačeno rozložení hladin akustického tlaku v prostoru. Na svislé ose diagramu je stupnice hladin akustického tlaku L [dB], na ose vodorovné je vzdálenost r [m] od zdroje zvuku. Jestliže se zvýší celková pohltivost prostoru například obložením stropu místnosti zvuk pohlcujícím obkladem, hladina v poli odražených vln L1 [dB] se sníží na hodnotu L2 [dB]. Zároveň se zvětší dozvuková vzdálenost z hodnoty rk1 [m] na hodnotu rk2 [m]. Z vyobrazení je zřejmé, že zvýšením celkové pohltivosti prostoru nelze snížit hladinu akustického tlaku v bezprostřední blízkosti zdroje, kde se nachází pole přímých vln. Hladinu akustického tlaku L [dB] v poli odražených vln je možno stanovit pomocí vztahu (68). Jeho odvození vychází z vlastností difúzního zvukového pole a respektuje zákon zachování energie. To znamená, že akustický výkon vyzařovaný zdrojem musí být celý pohlcován ohraničujícími povrchy místnosti. Po spuštění zdroje zvuku se hladina akustického tlaku v poli odražených vln ustálí právě na takové hodnotě, která zajistí stav rovnováhy mezi vyzářeným a pohlceným akustickým výkonem.
Difúzní charakter zvuku v poli odražených vln je určen třemi vlastnostmi:
- hustota akustické energie je ve všech místech difúzního pole stejná,
- každý směr dopadu zvuku je stejně pravděpodobný,
- hustota energie zvuku je součtem hustoty energie všech zvukových vln, které současně do daného místa z různých směrů přicházejí.
Uvedené vlastnosti difúzního pole lze vyjádřit následujícími vztahy:
Vlastnost 1: pro všechna místa v difúzním poli, která jsou určena souřadnicemi x, y, z [m] platí
Vlastnost 2: v každém místě difúzního pole platí
kde dΩ [sterad] je elementární prostorový úhel a dw [W.s.m−3] je elementární hustota akustické energie, která je do daného místa dodána akustickým vlněním ze směru určeného úhlem dΩ.
Vlastnost 3: hustotu akustické energie lze vyjádřit jako součet hustoty akustické energie zvukových vln přicházejících ze všech směrů
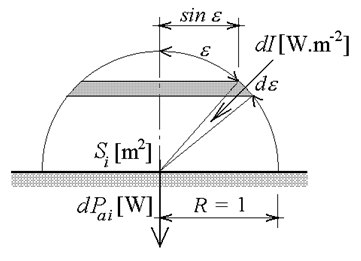
Obr. 20: K odvození vztahu (68)
Vynásobením rovnice (57) rychlostí zvuku c [m.s−1] lze obdržet
kde dI [W.m−2] je elementární akustická intenzita, která v daném místě působí ze směru určeného prostorovým úhlem dΩ. Veličinu IΣ [W.m−2] je možno definovat jako ekvivalentní intenzitu rovinné vlny ve volném zvukovém poli, která vzbudí stejný sluchový vjem jako difúzní zvukové pole v uzavřeném prostoru.
Na hranici difúzního pole vstupují zvukové vlny do interakce s ohraničující stěnou uzavřeného prostoru. Elementární intenzitu dI [W.m−2] příslušnou prostorovému úhlu dΩ je možno rozložit na složku dIn [W.m−2] kolmou a složku dIp [W.m−2] rovnoběžnou se stěnou.
kde ε [rad] je odklon směru působení zvukové vlny od normály stěny. Jen část dIai [W.m−2] kolmé složky intenzity je absorbována povrchem i-té plochy, která ohraničuje uzavřený prostor.
kde αi [-] je činitel pohltivosti i-tého ohraničujícího povrchu. Elementární akustický výkon dPai [W] pohlcený i-tou plochou Si [m2] se získá jako součin intenzity a plochy.
kde Ai [m2] je pohltivost i-té stěny uzavřeného prostoru.
Vztah (61) lze upravit rozšířením dΩ a dosazením podle vztahu (58)
Hodnotu akustického výkonu Pai [W] pohlceného i-tou stěnou uzavřeného prostoru lze obdržet integrací vztahu (62).
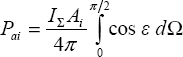 (63)
(63)Elementární prostorový úhel dΩ může být stanoven jako povrch elementárního kulového pásu podle obr. 20 dělený druhou mocninou poloměru myšlené kulové plochy. Při jednotkovém poloměru R = 1 myšlené kulové plochy lze napsat
a integrál (63) pak bude mít tvar (65), který lze řešit substitucí sin ε = t; cos ε . dε = dt
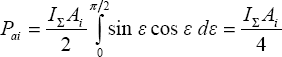 (65)
(65)Akustický výkon Pa [W] pohlcený v celém uzavřeném prostoru je roven součtu akustických výkonů pohlcených dílčími plochami.
kde n je počet dílčích ploch vnitřního prostoru a ![]() [m2] je celková pohltivost místnosti. Ze zákona zachování energie plyne rovnost mezi pohlceným akustickým výkonem Pa [W] a akustickým výkonem Pe [W] vyzářeným zdrojem zvuku.
[m2] je celková pohltivost místnosti. Ze zákona zachování energie plyne rovnost mezi pohlceným akustickým výkonem Pa [W] a akustickým výkonem Pe [W] vyzářeným zdrojem zvuku.
Známý vztah (68) pro výpočet hladiny akustického tlaku L [dB] v difúzním poli lze obdržet upravením rovnice (67), jejím vynásobením hodnotou 1012, logaritmováním a vynásobením deseti.
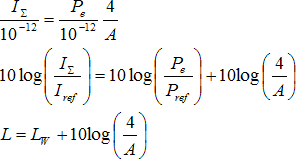 (68)
(68)kde Iref = 10−12 W.m−2 resp. Pref = 10−12 W jsou referenční hodnoty akustické intenzity resp. akustického výkonu a LW [dB] hladina akustického výkonu zdroje.
Se vzrůstající celkovou pohltivostí A [m2] místnosti se zvyšuje i hodnota středního činitele pohltivosti αm [-] uzavřeného prostoru a také se postupně omezuje a ruší difúznost zvukového pole v důsledku úbytku energie odražených zvukových vln, až při extrémní hodnotě αm = 1 odražené vlny a s nimi difúzní pole zcela mizí a v celém vnitřním prostoru je pouze pole přímých vln. Tím se ruší i předpoklady, na jejichž základě byl vztah (68) odvozen. Taková situace nastává např. v bezdozvukových místnostech akustických laboratoří, které slouží k měření zvuku ve volném poli v laboratorních podmínkách. Namísto vztahu (68) se proto v prostorech s vysokou pohltivostí používá vztah (69), kde výraz (1 − αm) kompenzuje ztrátu difúznosti při vyšších hodnotách αm.
αm [-] je střední činitel pohltivosti, který se stanoví jako průměrná hodnota ze všech povrchů v místnosti
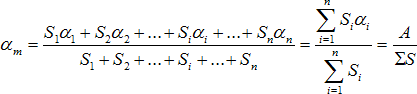 (70)
(70)kde Si [m2] je i-tý povrch s činitelem pohltivosti zvuku αi [-] a n je počet dílčích povrchů v místnosti. Jednotlivými povrchy mohou být např. strop, stěna, okno, dveře, koberec apod.
Hladinu akustického tlaku současně v poli přímých i odražených vln charakterizuje Berankův vztah (71) podle, který je kombinací již uvedených vztahů (37) a (69).
Jestliže se výraz v závorce ve vztahu (71) položí roven nule a vyjádří se r, získá se vztah pro výpočet dozvukové vzdálenosti
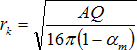 (72)
(72)