Intenzita zvuku – decibel
Mírou účinku mechanického vlnění vzduchu a jím přenášeného zvuku je plošná hustota akustického výkonu nazvaná akustická intenzita I [W.m−2]. Prahové hodnoty akustické intenzity již byly uvedeny (viz obr. 4). Citlivost lidského sluchu při vnímání akustické intenzity není vždy stejná, ale s rostoucí intenzitou se snižuje. Při zvyšování akustické intenzity jakoby sluchový orgán stále více ztrácel schopnost vnímat v plné hodnotě její další přírůstek. Výsledkem je logaritmická závislost mezi velikostí zvukového podnětu a velikostí sluchového vjemu, kterou objevil německý fyziolog Ernst Heinrich Weber (l795–1878) a kterou později zdůvodnil jiný německý badatel, zakladatel psychofyziky Gustav Theodor Fechner (1801–1887). Weber–Fechnerův psychofyzický zákon zní: Intenzita počitku je úměrná logaritmu podnětu.
Uvedená vlastnost sluchu není samoúčelná. Umožňuje totiž člověku vnímat i velmi slabé zvukové signály s vysokou citlivostí a zároveň ho chrání před zvukem vysoké intenzity. Tato vlastnost sluchu byla důvodem k zavedení logaritmické míry (decibelové stupnice) při kvantifikaci akustických veličin. Akustická intenzita I [W.m−2] vyjádřená v decibelech se nazývá hladina akustické intenzity L [dB]
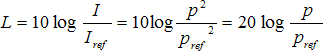 (29)
(29)kde Iref = 10−12 W.m−2 je jíž zmíněná prahová hodnota akustické intenzity. Intenzita je přímo úměrná druhé mocnině akustického tlaku.
Proto je ve vztahu (29) poměr intenzit nahrazen poměrem druhých mocnin akustického tlaku. Takto definovaná veličina se nazývá hladina akustického tlaku L [dB], kde pref = 2 ‧ 10−5 Pa je prahová hodnota akustického tlaku. Obě veličiny – hladina akustické intenzity sledovaná ve směru šíření zvuku a hladina akustického tlaku – mají vždy stejnou hodnotu, protože jsou tak záměrně definovány. Rozdíl mezi nimi spočívá ve směrovém působení. Jako vektor je intenzita úzce spojena i se směrem šíření zvuku, zatímco akustický tlak jen popisuje stav prostředí v daném místě bez ohledu na směr šíření zvuku. Proto hladina akustického tlaku má s hladinou akustické intenzity stejnou hodnotu jen tehdy, jestliže plocha, na které zjišťujeme intenzitu, je kolmá na směr šíření zvuku. Sluchový orgán člověka je schopen přijímat zvuk z jakéhokoli směru. Vnímání zvuku tak více souvisí s tlakem než s intenzitou. To je hlavní důvod, proč se v praxi při popisu „síly“ zvuku používá veličina: hladina akustického tlaku. Spíše pro teoretické úvahy je pak vhodná představa hladiny akustické intenzity.
| akustický tlak p [Pa] | akustická intenzita I [W.m−2] | hladina akustického tlaku L [dB] | příklad prostředí, kde se vyskytuje |
|---|---|---|---|
| cca 60 | cca 10 | cca 130 | práh bolesti |
| 2 | 10−2 | 100 | diskotéka |
| 0,2 | 10−4 | 80 | rušná ulice |
| 0,02 | 10−6 | 60 | kancelář |
| 0,002 | 10−8 | 40 | obývací pokoj |
| 0,0002 | 10−10 | 20 | ložnice v noci |
| 0,00002 | 10−12 | 0 | práh slyšení |
Je dobré si povšimnout, že v definičním vztahu (29) se logaritmuje bezrozměrné číslo (podíl akustických intenzit resp. podíl druhých mocnin akustických tlaků). V decibelech by tak mohla být vyjádřena jakákoliv jiná fyzikální veličina (stačilo by jen stanovit její prahovou hodnotu) a v tomto smyslu má decibel obdobný charakter jako například procento.
Protože se při hladinovém vyjádření velikosti akustických veličin pracuje s logaritmy jejich hodnot, dochází při počítání s hladinami k některým skutečnostem, které se vymykají běžnému chápání kvantity. Projevuje se to například při sčítání hladin.
Jsou známy hladiny L1 [dB] a L2 [dB] akustického tlaku generované dvěma různými zdroji zvuku. Úkolem je stanovit hladinu akustického tlaku při současném působení obou zdrojů. Sčítané intenzity zvuku jsou I1 [W.m−2] a I2 [W.m−2].
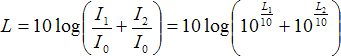 (31)
(31)Operace naznačená ve vztahu (31) se nazývá energetický součet.