Útlum zvuku ohybem přes překážku
Za každou překážkou na cestě šíření zvuku, jejíž rozměry převyšují vlnovou délku, se vytváří zvukový stín, ve kterém lze pozorovat snížení intenzity zvuku oproti stavu volného šíření zvukových vln bez překážky. Útlum intenzity zvuku závisí na poloze zdroje zvuku, na poloze a geometrickém tvaru překážky, na poloze pozorovatele za překážkou a na vlnové délce zvuku. Vznik a vlastnosti zvukového stínu lze vysvětlit pomocí ohybu vlnění. Zákonitosti ohybu platí pro každé vlnění, tedy i pro vlnění elektromagnetické včetně světla, a právě pro světlo byly tyto zákonitosti nejdříve popsány. Princip šíření vlnění formuloval holandský astronom, fyzik a matematik Christian Huygens (1629–1695): Každý bod vlnoplochy je elementárním zdrojem vlnění. Výsledná vlnoplocha má tvar obálky dílčích vlnoploch. Tímto principem se vysvětluje pouze tvar vlnoploch za překážkou (viz obr. 13), nikoli však intenzita.
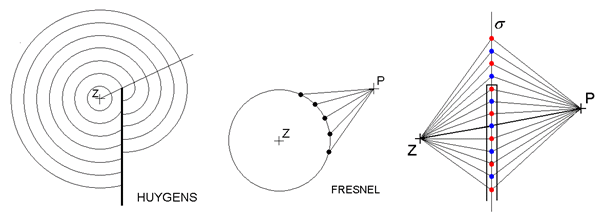
Obr. 13: Šíření vlnění podle Huygense a podle Fresnela
Augustin Jean Fresnel (l788–1827) – [čti frenel] – byl francouzský fyzik. Zdůvodnil vlnovou teorii světla a mimo jiné na základě Huygensova principu a vlnové interference vysvětlil jeho ohyb. Příslušné zákonitosti platí i pro zvuk. V oblasti praktických aplikací jeho objevů je známá Fresnelova čočka stupňovitě tvořená soustavou soustředných zobrazovacích prvků. Huygensův princip doplnil Fresnel v tomto smyslu: Při sledování intenzity je nutno přihlédnout k interferenci (skládání vlnění). K intenzitě vlnění v bodě P (viz. obr.) přispívá každý z elementárních zdrojů vlnění – bodů vlnoplochy. Jednotlivé body vlnoplochy jsou však od bodu P různě vzdáleny. Je-li tato vzdálenost sudým násobkem půlvlny, přispěje takový elementární zdroj ke zvýšení intenzity v bodě P. Naopak při vzdálenosti rovné lichým násobkům půlvlny bude vlnění přicházející z příslušného elementárního zdroje v opačné fázi a bude intenzitu snižovat.
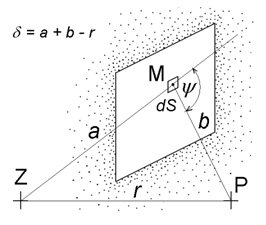
Obr. 14: K ohybu zvuku
Úvahu je možno zobecnit tím, že namísto souboru elementárních zdrojů na kulové vlnoploše lze uvažovat soubor elementárních zdrojů na jakékoli ploše ležící mezi zdrojem Z a místem příjmu P. Podmínkou je jen to, aby zvolenou plochou procházely všechny možné cesty šíření vln ze zdroje Z do bodu P. S výhodou se za plochu elementárních zdrojů volí rovina σ stínící překážky. Od bodového zdroje Z se zvukové vlny šíří všemi směry a postupně zasáhnou všechny body roviny σ. Každý bod této roviny kmitá s jinou fází tak, jak k němu vlnění s různým časovým zpožděním dospělo. Každý z těchto bodů je zároveň elementárním zdrojem vlnění pro příjemce P zvuku. Celý soubor elementárních zdrojů zvuku v rovině σ musí mít v místě příjmu stejný účinek, jako původní zdroj. Přes různé body roviny σ přichází vlnění do místa příjmu po jiné dráze a tedy s jiným fázovým zpožděním. Vlnění přicházející z místa původního zdroje přímou cestou se skládá s vlněním z jiných směrů, přičemž příspěvky od různých elementárních zdrojů v rovině σ přicházejí do místa příjmu v různé míře se shodnou fází nebo ve fázi opačné a způsobují tak buď zesílení (viz místa vyznačená na obrázku 13 modře) nebo zeslabení (viz místa vyznačená červeně) přímého signálu. Účinek příspěvků od různých elementárních zdrojů roviny σ se tak navzájem ruší a při interferenci vlnění v místě příjmu dominuje jen přímá cesta zvuku. Tato rovnováha se poruší, postaví-li se do cesty vlnění překážka. Část elementárních zdrojů roviny σ včetně přímé cesty zvuku je vyřazena z provozu a dochází k útlumu zvuku ohybem.
Činitel útlumu d [-] intenzity vlnění při jeho ohybu přes překážku se definuje jako poměr intenzit
(38)kde I1 resp. I2 [W.m−2] je intenzita zvuku v místě P bez uvažování resp. s uvažováním vlivu clony. Intenzita zvuku je přímo úměrná druhé mocnině efektivní hodnoty akustického tlaku pef [Pa]. Efektivní hodnota je pak přímo úměrná amplitudě akustického tlaku A [Pa] při harmonickém vlnění. Činitel útlumu lze proto vyjádřit jako poměr druhých mocnin amplitud akustického tlaku
(39)kde A1 resp. A2 [Pa] je amplituda akustického tlaku v místě P bez clony resp. se clonou. Útlum D [dB] hladiny akustického tlaku způsobený clonou bude pak
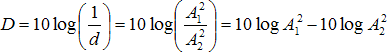(40)V souladu se vztahem (18) platí pro akustický tlak při harmonickém vlnění vztah
(41)kde φ = k ‧ x [rad] je fázový rozdíl. Jako počátek sledování se označí okamžik, kdy vlnění dospělo do místa P po přímé cestě ze zdroje Z. Část akustického tlaku p0 [Pa], která je způsobena jen tímto přímým šířením, lze popsat vztahem
(42)kde amplituda A0 [Pa] závisí jen na výkonu zdroje a vzdálenosti r [m]. Fázový rozdíl je nulový, protože na počátku sledování vlnění právě dospělo přímou cestou do místa P a je tedy na počátku vlny. Dalšími cestami (např. i přes bod M – viz obr. 14) dospěje vlnění do bodu P s časovým zpožděním a tedy i s fázovým rozdílem. Proto lze předpokládat, že akustický tlak p [Pa] v místě P vzniklý jako výsledek spolupůsobení všech cest šíření (přes všechny elementární zdroje roviny σ) bude obsahovat nenulový fázový rozdíl φ [rad] a bude tedy odpovídat vztahu (41). Cílem následujících úvah je stanovit hodnotu amplitud akustického tlaku A1 a A2 [Pa] pro použití ve vztazích (39) a (40).
Vztah (41) lze upravit jako sinus rozdílu dvou úhlů
(43)Příspěvek dp [Pa] elementární plochy dS [m2] části roviny σ v místě bodu M k hodnotě akustického tlaku v bodě P je
(44)K.dS [Pa] je amplituda zahrnující vliv A0, δ, ψ, dS
c [m.s−1] je rychlost zvuku ve vzduchu
δ/c [s] je časové zpoždění vlny vzhledem k počátku sledování.
δ = a + b – r [m] je rozdíl drah zvuku mezi dráhou přes bod M a dráhou přímou – viz obr. 14
Vztah (44) je možno upravit roznásobením závorky a dosazením vlnového čísla 
(45)Hodnota akustického tlaku v bodě P se získá integrací přes celou volnou část roviny σ (například přes plochu vyznačenou jako „okno“ na obrázku 14).
(46)Integrál je možno upravit s využitím vztahu pro sinus dvou úhlů
(47)Integrály ve vztahu (47) se nazývají Fresnelovy integrály a označují se
(48a)
(48b)Vztah (47) pak bude mít tvar
(49)Porovnáním vztahu (49) se vztahem (43) se snadno zjistí že
(50a)
(50b)Hledanou druhou mocninu amplitudy A [Pa] akustického tlaku v bodě P pak lze stanovit právě pomocí Fresnelových integrálů.
(51)S přihlédnutím ke vztahům (39) a (40) je pak možno pomocí Fresnelových integrálů stanovit činitel d [-] útlumu a útlum D [dB] hladiny akustického tlaku.
(52)
(53)kde X1 a Y1 resp. X2 a Y2 jsou hodnoty příslušných Fresnelových integrálů stanovené integrací po celé volné části roviny σ za stavu bez clony resp. za stavu se clonou.
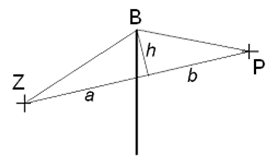
Obr. 15: Ke stanovení proměnné veličiny u
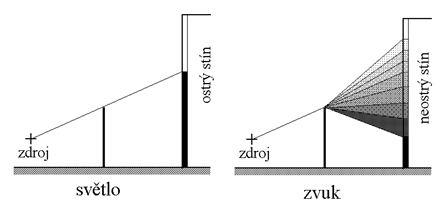
Při výpočtu Fresnelových integrálů se zavádí nová proměnná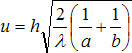 
, kde h [m] je výška trojúhelníka ZPB (obr. 15), a a b [m] jsou úseky základny ZP trojúhelníka vymezené patou této výšky. Je-li výška h významně menší v porovnání se vzdálenostmi a a b, pak 
, kde 
[-] je Fresnelovo číslo.
Fresnelovy integrály pak mají tvar
(54a)
(54b)Hodnoty Fresnelových integrálů se stanoví s požadovanou přesností jako konvergující součty číselných řad. Pro praktickou potřebu jsou tabelovány – viz tabulka 7. Platí
| u | X | Y | u | X | Y | u | X | Y | u | X | Y |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,00 | 0,0000 | 0,0000 | 2,00 | 0,4982 | 0,3434 | 4,00 | 0,4984 | 0,4204 | 5,50 | 0,4784 | 0,5537 |
| 0,10 | 0,1000 | 0,0005 | 2,10 | 0,5815 | 0,3743 | 4,10 | 0,5738 | 0,4758 | 5,55 | 0,4456 | 0,5181 |
| 0,20 | 0,1999 | 0,0042 | 2,20 | 0,6363 | 0,4557 | 4,20 | 0,5418 | 0,5633 | 5,60 | 0,4517 | 0,4700 |
| 0,30 | 0,2994 | 0,0141 | 2,30 | 0,6266 | 0,5531 | 4,30 | 0,4494 | 0,5540 | 5,65 | 0,4926 | 0,4441 |
| 0,40 | 0,3975 | 0,0334 | 2,40 | 0,5550 | 0,6197 | 4,40 | 0,4383 | 0,4622 | 5,70 | 0,5385 | 0,4595 |
| 0,50 | 0,4903 | 0,0647 | 2,50 | 0,4574 | 0,6192 | 4,50 | 0,5261 | 0,4342 | 5,75 | 0,5551 | 0,5049 |
| 0,60 | 0,5811 | 0,1105 | 2,60 | 0,3890 | 0,5500 | 4,60 | 0,5673 | 0,5162 | 5,80 | 0,5298 | 0,5461 |
| 0,70 | 0,6597 | 0,1721 | 2,70 | 0,3925 | 0,4529 | 4,70 | 0,4914 | 0,5672 | 5,85 | 0,4819 | 0,5513 |
| 0,80 | 0,7230 | 0,2493 | 2,80 | 0,4675 | 0,3915 | 4,80 | 0,4338 | 0,4968 | 5,90 | 0,4486 | 0,5163 |
| 0,90 | 0,7648 | 0,3398 | 2,90 | 0,5626 | 0,4101 | 4,90 | 0,5002 | 0,4350 | 5,95 | 0,4566 | 0,4688 |
| 1,00 | 0,7799 | 0,4383 | 3,00 | 0,6058 | 0,4963 | 5,00 | 0,5637 | 0,4992 | 6,00 | 0,4995 | 0,4470 |
| 1,10 | 0,7638 | 0,5365 | 3,10 | 0,5616 | 0,5818 | 5,05 | 0,5450 | 0,5442 | 6,05 | 0,5424 | 0,4689 |
| 1,20 | 0,7154 | 0,6234 | 3,20 | 0,4664 | 0,5933 | 5,10 | 0,4998 | 0,5624 | 6,10 | 0,5495 | 0,5165 |
| 1,30 | 0,6386 | 0,6863 | 3,30 | 0,4058 | 0,5192 | 5,15 | 0,4553 | 0,5427 | 6,15 | 0,5146 | 0,5496 |
| 1,40 | 0,5431 | 0,7135 | 3,40 | 0,4385 | 0,4296 | 5,20 | 0,4389 | 0,4969 | 6,20 | 0,4676 | 0,5398 |
| 1,50 | 0,4453 | 0,6975 | 3,50 | 0,5326 | 0,4152 | 5,25 | 0,4610 | 0,4536 | 6,25 | 0,4493 | 0,4954 |
| 1,60 | 0,3655 | 0,6389 | 3,60 | 0,5880 | 0,4923 | 5,30 | 0,5078 | 0,4405 | 6,30 | 0,4670 | 0,4555 |
| 1,70 | 0,3238 | 0,5492 | 3,70 | 0,5420 | 0,5750 | 5,35 | 0,5490 | 0,4662 | 6,35 | 0,5240 | 0,4560 |
| 1,80 | 0,3336 | 0,4508 | 3,80 | 0,4481 | 0,4481 | 5,40 | 0,5573 | 0,5140 | 6,40 | 0,5496 | 0,4965 |
| 1,90 | 0,3944 | 0,3734 | 3,90 | 0,4223 | 0,4223 | 5,45 | 0,5269 | 0,5519 | 6,45 | 0,5292 | 0,5398 |
Obr. 16: Porovnání ohybu světla a zvuku
Zajímavé je srovnání mezi ohybem světla a ohybem zvuku. Vlnová délka světla je 3,8.10−7 až 7,8.10−7 m a hodnota Fresnelova čísla N vychází proto velmi vysoká již při nepatrném rozdílu drah δ [m]. U zvuku, jehož vlnová délka při šíření ve vzduchu se pohybuje v rozmezí 0,02 až 20 m, je hodnota Fresnelova čísla N v porovnání se světlem malá a menší je proto i útlum, který překážka způsobuje. Zvukové vlny zejména nízkého kmitočtu se snáze ohýbají přes překážku a zvukový stín je podstatně méně ostrý. Útlum zvuku lze zaznamenat dokonce i v místech se zápornou hodnotou dráhového rozdílu δ [m] a tedy i zápornou hodnotou Fresnelova čísla N tj. v místech, kam světelné vlny dopadají bez omezení, takže zdroj zvuku lze z těchto míst přes překážku pozorovat.
Protože přesný výpočet útlumu pomocí Fresnelových integrálů je relativně pracný, snažili se v minulosti různí autoři o zjednodušení. Jeden z možných postupů spočívá ve využití diagramu prof. Maekawy. Hodnota útlumu D [dB] se vyhledá v diagramu na obrázku 17 v závislosti na Fresnelově čísle N [-].
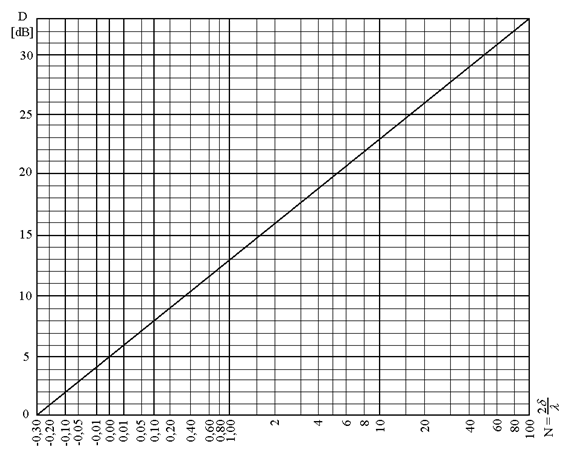
Obr. 17: Útlum zvuku ohybem přes překážku v závislosti na Fresnelově čísle (podle prof. Maekawy)
