Předpjaté ocelové tlačené trubky s jedním křížem
Článek se zabývá návrhem velmi štíhlých tlačených ocelových prvků. Návrhová únosnost běžných štíhlých tlačených sloupů je dána jejich vzpěrnou únosností, která je při velké štíhlosti malá. Modifikací štíhlého sloupu do vzpínadlového předpjatého systému vede k násobnému zvýšení návrhové únosnosti. V článku jsou popsány předpjaté vzpínadlové ocelové tlačené trubky s jedním křížem. Uvádějí se vztahy pro stanovení kritického zatížení „ideálního vzpínadlového prutu“ a dále vztahy pro určení maximální únosnosti „imperfektního vzpínadlového prutu“. Maximální únosnosti po redukci součinitelem materiálu vedou ke stanovení návrhové únosnosti v souladu s Eurokódem 1993-1-1. V závěru je uveden příklad výpočtu a porovnání únosností předpjatého (vzpínadlového) a nepředpjatého (běžného) prutu velké štíhlosti.
1. Úvod
Chování tlačeného štíhlého prutu závisí na jeho geometrických a materiálových vlastnostech. Ideální prut (dokonale přímý a bez reziduálních pnutí) ztrácí stabilitu (vybočuje) při dosažení kritického zatížení, zatímco únosnost reálného prutu s počátečními imperfekcemi (prohnutím a reziduálními pnutími) je závislá též na tvaru a velikosti imperfekcí a definici únosnosti (např. únosnost daná dosažením kluzu v nejvíce namáhaných vláknech, tj. vzpěrná únosnost podle současných norem, nebo maximální dosažitelná plastická únosnost, kdy prut opravdu více nepřenese a kolabuje). Únosnost reálného prutu je vždy nižší než jeho kritické zatížení.
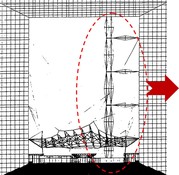
Velmi štíhlé pruty jsou žádány jako estetické pohledové prvky, ale velká štíhlost limituje kritické zatížení i únosnost. Použitím předpjatých vzpínadlových prutů lze obě hodnoty násobně zvýšit za cenu zvýšených nákladů na výrobu a montáž, ale i ovlivnit estetické vnímání konstrukce (obr. 1).
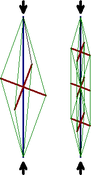
Vzpínadlový prut je obvykle tvořen hlavní trubkou s rozpětím L, navařeným trubkovým křížem se čtyřmi rameny s délkou a v úhlu 90° a lanky nebo tyčemi pro vnesení předpětí. Realizovány však byly i pruty s více kříži, popř. kříži se třemi rameny v úhlu 120°, nebo pruty pouze se dvěma rameny v rovinném uspořádání (v kolmém směru k této rovině je potom vybočení příslušně bráněno), obr. 2.
2. Stabilita ideálního vzpínadlového prutu s jedním křížem
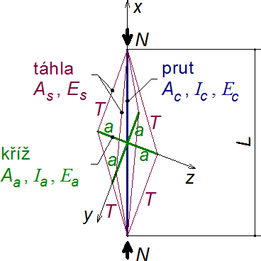
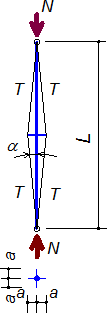
Kritické zatížení Ncr prutu v základním uspořádání podle obr. 3 lze odvodit z geometrických vztahů, podmínek rovnováhy a Hookova zákona (Smith a kol. [1], Hafez a kol. [2]). Základní předpoklady analytického odvození:
- zatížení je v ose hlavního prutu, který je ideálně přímý a bez reziduálních pnutí,
- spojení mezi hlavním prutem a rameny kříže je tuhé,
- spojení táhel s hlavním prutem a rameny kříže je neposuvné kloubové,
- osová deformace ramen kříže je zanedbána,
- vybočení nastává v rovině ramen.
Pozn.: V důsledku předpokladů 4 a 5 se výsledné kritické zatížení z analytického výpočtu bude poněkud lišit od numerického řešení vhodným softwarem MKP.
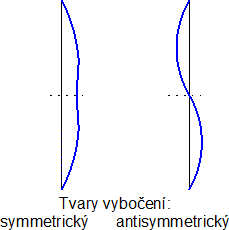
Hlavní prut může vybočit v symetrickém nebo antisymetrickém tvaru (obr. 3). Tvar vybočení ovlivňuje geometrie uspořádání (krátká ramena vedou obvykle k symetrickému vybočení), tuhostní poměry mezi hlavním prutem a rameny a též velikost předpětí táhel.
| Charakteristiky základního prutu (délka L): | |
| Ac [mm2], Ic [mm4], Ec [MPa] | plocha, moment setrvačnosti, modul pružnosti, |
| osová a ohybová konstanta celého prutu. | |
| Charakteristiky ramene kříže (délka a): | |
| Aa [mm2], Ia [mm4], Ea [MPa] | plocha, moment setrvačnosti, modul pružnosti, |
| osová a ohybová konstanta ramene kříže. | |
| Charakteristiky táhel (délka Ls): | |
| As [mm2], Es [MPa] | plocha, modul pružnosti. |
| osová konstanta táhla. | |
Kritické zatížení hlavního prutu lze vyjádřit obvyklým vztahem:
kde ohraničující limity plynou z okrajových podmínek:
- pro prut bez táhel β = 1 (tj. Ncr = NE, Eulerova síla),
- pro prut s nekonečně tuhými rameny kříže a nekonečně tuhými táhly, tj. prut v místě kříže vetknutý:
β = 0,35 (tj. Ncr ≈ 8,18 NE).
Kritické zatížení prutu se tedy může pohybovat mezi (NE a 8,18 NE).
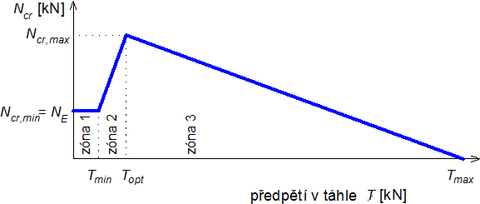
Z analytického řešení předpjatých vzpínadlových prutů [2] plyne, že velikost kritického zatížení pro dané charakteristiky závisí na velikosti předpětí táhel. Jak ukazuje graf na obr. 4, předpětí (v každém táhle označeno písmenem T ) vymezuje 3 oblasti chování vzpínadlového prutu:
Zóna 1: Předpětí je velmi nízké (T < Tmin), takže při zatížení tah v táhlech vymizí, prut se chová jako bez táhel a kritické zatížení prutu dosáhne pouze Eulerovy síly NE = Ncr,min. Pro minimální předpětí platí:
kde parametr C1:
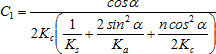 (3)
(3)
Pro prostorové uspořádání (4 táhla) n = 4, pro rovinné uspořádání (2 táhla) n = 2.
Zóna 2: Předpětí T je větší než minimální Tmin, ale menší nebo rovné optimálnímu předpětí Topt, při kterém má kritické napětí největší hodnotu Ncr,max. Předpětí v táhlech je v této oblasti aktivní (nenulové) až do okamžiku vybočení. Kritická síla prutu v této oblasti plyne ze vztahu:
Zóna 3: Předpětí T je větší než optimální Topt. V tomto případě zůstávají táhla při vybočení aktivní (napjatá). Účinek předpětí v táhlech zvyšuje zatížení a tím snižuje kritické napětí prutu. Maximální předpětí, které vyvolá samo o sobě vybočení prutu, je dáno vztahem:
kde opět pro prostorové uspořádání (4 táhla) n = 4, pro rovinné uspořádání (2 táhla) n = 2.
Kritická síla prutu v této oblasti plyne ze vztahu:
a pro parametr C2 platí:
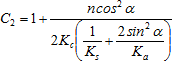 (7)
(7)
Stanovení maximální kritické síly prutu Ncr,max závisí na předpokládaném tvaru vybočení (obr. 3) a plyne z řešení goniometrických rovnic pro hodnotu kl, danou výrazem:
Pro symetrický tvar vybočení je nutné splnit rovnici:
Pro antisymetrický tvar vybočení je nutné splnit rovnici:
Maximální dosažitelné kritické zatížení (obr. 4):
Po vyřešení hodnot kl pro oba tvary vybočení plyne kritické zatížení ze vztahu (11), pro menší z obou hodnot kl:
Optimální předpětí (obr. 4):
3. Únosnost skutečného imperfektního vzpínadlového prutu s jedním křížem
Imperfektní prut lze analyzovat jednak z hlediska pružné nelineární stability (dává obraz o kritickém zatížení v celém rozsahu předpětí a skutečném tvaru vybočení), nebo z hlediska maximální únosnosti při daných imperfekcích (pro spolehlivý návrh).
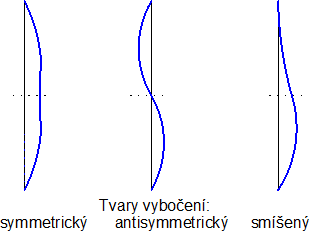
Obr. 5. Tvary vybočení při nelineární analýze imperfektního vzpínadlového prutu
Z numerických studií nelineární pružné stability MKP (Saito a kol. [3], Píchal a Macháček [4]) pro reálné imperfekce ve tvaru symetrického, antisymetrického a interaktivního vybočení podle obr. 5 a maximální amplitudu L/200 až L/300 v souladu s Eurokódem (EN 1993-1-1) vyplývá, že pro reálný vzpínadlový prut s předpětím blízkým optimálnímu předpětí Topt podle vztahu (12) je tvar vybočení obvykle interaktivní a často v praxi užívaný návrh na druhý tvar vybočení nemusí být konzervativní.
Experimenty (Osofero a kol. [5]) na 18 vzpínadlových předpjatých prutech ukázaly, že pokud rozhoduje symetrické vybočení, vyšší předpětí zvyšuje únosnost konstrukce (důvodem je aktivní zapojení všech 4 lanek). Naopak rozhoduje-li antisymetrické, popř. interaktivní vybočení, zvyšování předpětí vede ke snížení únosnosti (protože táhla na konkávní straně zvyšují ohyb hlavního prutu).
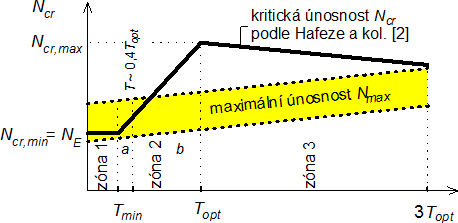
Obr. 6. Únosnosti předpjatých prutů ve vztahu ke kritickému zatížení
Únosnost Nmax vyšetřovali MKP (ABAQUS software) v parametrické studii Wadee a kol. [6] a výsledky upravili v souladu s experimenty. Ukázalo se, že únosnost imperfektních předpjatých prutů je v zóně 1 a zóně 2 do předpětí cca 0,4 Topt vyšší než kritická, zatímco pro vyšší předpětí a v zóně 3 až do předpětí 3Topt nižší než kritická (viz schéma na obr. 6). Obdobné, podrobnější vysvětlení, podali Píchal a Macháček [7]. Pro stabilní chování konstrukce se doporučuje předpětí v rozsahu 2Topt ÷ 3Topt, pro něž je pokles kritického zatížení od maximální hodnoty malý a naopak únosnost roste.
Maximální únosnosti Nmax podle obr. 6 jsou pro různé amplitudy počátečních prohnutí (tzv. „ekvivalentní imperfekce“) pro symetrické i antisymetrické tvary vybočení a předpětí Tmin, Topt a 3Topt uvedeny v tabulkách 1 a 2 [6].
| Amplituda ekvivalentní imperfekce | (Nmax/Ncr,max)sym,zóna1 | (Nmax/Ncr,max)sym,Topt | (Nmax/Ncr,max)sym,3Topt |
|---|---|---|---|
| L/1000 | 19,0(2a/L) + 0,10 | 14,0(2a/L)2 − 3,1(2a/L) + 0,75 | 1,00 − 1,2(2a/L) |
| L/400 | 17,0(2a/L) + 0,13 | 58,0(2a/L)2 − 14,1(2a/L) + 1,16 | 0,84 − 1,2(2a/L) |
| L/200 | 13,5(2a/L) + 0,28 | 0,71 − 3,0(2a/L) | 0,72 − 1,4(2a/L) |
| Amplituda ekvivalentní imperfekce | (Nmax/Ncr,max)anti,zóna1 | (Nmax/Ncr,max)anti,Topt | (Nmax/Ncr,max)anti,3Topt |
|---|---|---|---|
| L/1000 | 1,00(2a/L) + 0,80 | 1,50(2a/L) + 0,25 | 0,74 |
| L/400 | 0,80(2a/L) + 0,63 | 0,70(2a/L) + 0,33 | 0,58 |
| L/200 | 0,70(2a/L) + 0,44 | 0,60(2a/L) + 0,20 | 0,43 |
Únosnost předpjatého vzpínadlového prutu pro dané předpětí táhel T lze potom stanovit z těchto tabulkových hodnot lineární interpolací v souladu s obr. 6. Amplitudu ekvivalentní počáteční imperfekce lze při návrhu volit podle Eurokódu ČSN 1993-1-1, tabulky 5.1 (pro trubky válcované za tepla hodnotou L/300, pro trubky tvarované za studena hodnotou L/200). Rozhodnutí, zdali rozhoduje symetrické nebo antisymetrické vybočení, je nutné vyhodnotit z obou možností. Interpolační vztahy pro libovolné předpětí lanek T jsou dále uvedeny:
Symetrické vybočení (obvykle rozhoduje pro poměr 2a/L Є (0,05, 0,175):
- předpětí T Є (Tmin, 0,4Topt) → tj. první část zóny 2 (a):
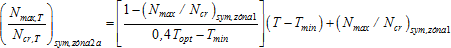 (13)
(13)
- předpětí T Є (0,4Topt, Topt) → tj. druhá část zóny 2 (b):
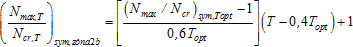 (14)
(14)
- předpětí T ≥ Topt → tj. zóna 3:
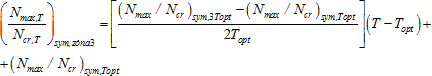 (15)
(15)
Antisymetrické vybočení (obvykle rozhoduje pro poměr 2a/L > 0,175):
- předpětí T ≤ Tmin → tj. zóna 1: konstantní hodnoty jsou ve druhém sloupci tab. 2.
- předpětí T Є (Tmin, Topt) → tj. zóna 2:
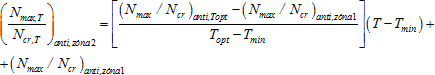 (16)
(16)
- předpětí T ≥ Topt → tj. zóna 3:
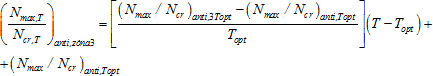 (17)
(17)
4. Závěr
Kritické zatížení ideálního tlačeného prutu i skutečnou únosnost imperfektního tlačeného prutu lze výrazně zvýšit předepnutím prostřednictvím táhel vedených přes středový kříž. Běžné jsou vzpínadlové tlačené sloupy z trubek, u nichž lze teoreticky dosáhnout zvýšení kritické síly až na 8,18 Eulerovy síly a několikanásobné zvýšení kolapsové únosnosti oproti nepředpjatému prutu.
Pro praktický návrh vzpínadlového prutu dané geometrie, průřezů a materiálů jsou uvedeny vztahy pro stanovení tvaru jeho vybočení, optimální předpětí táhel a maximální teoretické pružné únosnosti.
Na FSv ČVUT byl proveden experimentální i teoretický výzkum, který zahrnuje vzpínadlové trubkové tlačené prvky z běžné i korozivzdorné (nerezové) oceli, táhly z lanek i tyčí a s jedním nebo dvěma kříži [7], [8].
5. Příklad
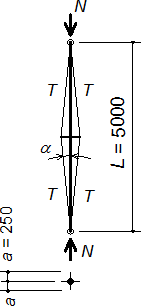
Obr. 7. Geometrie
Výše uvedené vztahy jsou použity pro určení návrhové únosnosti tlačené vzpínadlové trubky z austenitické nerezové oceli 1.4301 (mez kluzu fy = 210 MPa, modul pružnosti E = 200 GPa).
Geometrie a parametry prutu (obr. 7):
Hlavní trubka 50×2 [mm], L = 5000 mm:
Rameno trubkového kříže 25×1,5 [mm], a = 250 mm:
Táhla z nerezových lanek Macalloy 1×19, Ø 4 mm (Nmax = 12,6 kN, NRd = Nmax/1,5γR = 12,6/(1,5‧1,0) = 8,4 kN, E = 107 GPa):
Eulerova kritická síla nepředpjatého prutu:
Úhel lanek s hlavním prutem: α = 5,71° (tj. cos α = 0,995; sin α = 0,0994).
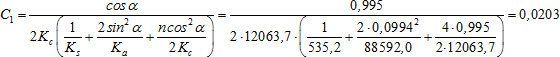
Symetrické vybočení, rovnice (9):
Řešení je (kl)sym = 3,105.
Antisymetrické vybočení, rovnice (10):
Řešení je (kl)anti = 3,602.
Rozhoduje menší kritické zatížení, tj. symetrické vybočení, takže z rovnice (11) plyne:
Optimální předpětí z rovnice (12):
Podle doporučení uvedeného v odstavci 3 je voleno stabilní návrhové předpětí T = 2Topt = 2 ‧ 545 = 1090 N < NRd = 8400 N. Pro trubku válcovanou za studena je podle Eurokódu 3 počáteční imperfekce L/200. Odtud pro rozhodující symetrické vybočení a imperfekci L/200 z tabulky 1 a rov. (15) plyne:
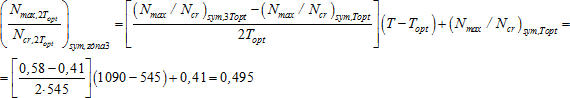
Kritické zatížení pro předpětí každého táhla 2Topt = 1090 N plyne ze vztahu (6) v zóně 3:
kde podle vztahu (7):
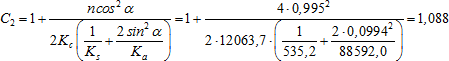
Odtud teoretická únosnost pro předpětí 2Topt :
Návrhová únosnost pro nerezovou ocel (γM1 = 1,1):
Poznámka:
Tuto únosnost lze porovnat s únosností stejného, ale nepředpjatého prutu z nerezové oceli 1.4301 podle Eurokódu ČSN EN 1993-1-4, pro nějž vychází: Ncr = 6870 N, štíhlost ![]() , α = 0,49,
, α = 0,49, ![]() , součinitel vzpěrnosti χ = 0,033. Odtud pro návrhovou únosnost plyne:
, součinitel vzpěrnosti χ = 0,033. Odtud pro návrhovou únosnost plyne:
Plná prostá únosnost tlačeného prutu činí:
Poměr návrhových únosností předpjatého a nepředpjatého prutu tedy činí: 11017/1900 = 5,8.
6. Oznámení
Článek a související výzkum vznikl za podpory grantu GAČR č. 17-24769S.
7. Literatura
- Smith, R.J., McCaffrey, G.T., Ellis, J.S.: Buckling of a single cross-arm stayed column. Journal of the Structural Division ASCE ST1, Jan. 1975, s. 249–288.
- Hafez, H.H., Temple, M.C., Ellis, J.S.: Pretensioning of single-crossarm stayed columns. Journal of the Structural Division ASCE ST2, Feb. 1979, s. 359–375.
- Saito, D., Wadee, M.A.: Numerical studies of interactive buckling in prestressed steel stayed columns. Engineering Structures, 31, 2009, s. 432–443.
- Píchal, R., Macháček, J.: Buckling and post-buckling of prestressed stainless steel stayed columns, Procedia Engineering, Vol. 172, 2017, pp. 875–882.
- Osofero, A.I., Wadee, M.A., Gardner, L.: Experimental study of critical and post-buckling behaviour of prestressed styed columns. Journal of Constructional Steel Reesearch, 79, 2012, s. 226–241.
- Wadee, M.A., Gardner, L., Osofero, A.I.: Design of prestressed stayed columns. Journal of Constructional Steel Reesearch, 80, 2013, s. 287–298.
- Píchal, R. – Macháček, J.: Single-crossarm stainless steel stayed columns, Advances in Technology Innovation, Vol. 3, No. 1, 2018, pp. 9–16.
- Macháček J. – Pichal, R.: Buckling and collapse capacity of prestressed steel tube stayed columns with one and two crossarms, Thin-Walled Structures, Vol. 132, 2018, s. 58–68.
V příspěvku je rozpracována statická analýza tlačeného vzpinadlového prutu se čtyřmi táhly a jedním křížem s pravoúhlými rameny stejné délky umístěnými v polovině délky štíhlého prutu. Uvažované uspořádání lze charakterizovat výrazným estetickým účinem při možnosti efektivního, spolehlivého a hospodárného využití předepnutých táhel vedených přes středový kříž. Řešení vychází z kritického zatížení (stability) ideálního prutu bez imperfekcí a následně se zaměřuje na problém únosnosti skutečného vzpinadlového prutu s jedním křížem a vlivem imperfekcí. Analýza skutečného prutu s uvážením tvaru a velikosti počátečního zakřivení navazuje na citaci příspěvků [6], [7] a je rozpracována ve smyslu současného pojetí teorie a metod navrhování nosných ocelových konstrukcí. Obsah příspěvku a výklad řešení příslušných problémů doplňuje účelně a názorně doložený příklad. S ohledem na jednoznačnost vhodného využití předloženého příspěvku pro potřeby praxe i jeho kvalifikované a odborné rozpracování doporučuji příspěvek k publikaci na portálu TZB info.
The article deals with a design of very slender steel columns loaded in compression. The design resistance of common compression columns results from the buckling resistance, which is due to a high slenderness low. Modification of a common column into a stayed prestressed system leads to a multiple increase of its design resistance. The article describes prestressed steel stayed columns with one central crossarm. First the formulas for critical loads of “ideal stayed columns” are presented, second the formulas for maximal resistances of “imperfect stayed columns” are given. The reduction of the maximal resistances by a material partial safety factor results into a design resistances in accordance with Eurocode 1993-1-1. Finally a solved example is presented with a comparison of resistances received for the prestressed (stayed) column and non-prestressed (common) column with a very high slenderness.