Ocelové oblouky stabilizované membránami. Část 2: Parametrické studie ocelových oblouků stabilizovaných membránami
V textu je parametricky vyšetřována stabilita a vybočení podpěrných oblouků válcové membránové konstrukce pomocí lineární bifurkační analýzy. Pro široké spektrum praktických geometrických parametrů konstrukce, předpětí membrán, způsobů uložení oblouků i čel membrány jsou uvedeny součinitele vzpěrných délek pro vybočení v rovině i z roviny oblouků a porovnány se stejnými součiniteli samostatných oblouků. Článek navazuje na Část 1: Experimenty a analýza [1], kde je uveden numerický model v programu SOFiSTiK a jeho validace pro membránové konstrukce podepřené ocelovými oblouky.
1. Úvod
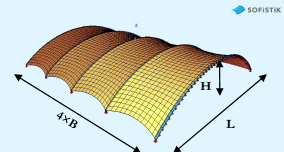
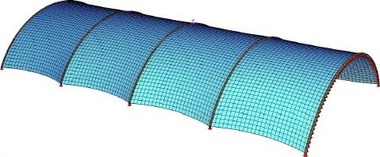
Membránové konstrukce válcového tvaru podepírané ocelovými oblouky jsou navrhovány pro velkorozponové moderní konstrukce i malé světlíky (obr. 1). Testy s textilní membránou podporovanou trubkovými ocelovými oblouky, popis obvyklých materiálů membrán, návrh membránových konstrukcí a jejich numerická analýza byly podrobně popsány v Části 1 [1]. Modelování v softwaru SOFiSTiK bylo úspěšně validováno na výsledcích testů a stejná numerická analýza je použita v této navazující Části 2.
Cílem studie je vyšetření stability podpěrných oblouků stabilizovaných membránou. Testy i numerické studie uvedené v Části 1 prokázaly enormní stabilizační efekt pro vybočení jak v rovině, tak z roviny oblouků. V parametrické studii jsou proto stanoveny součinitele vzpěrné (kritické) délky oblouků stabilizovaných membránou a porovnány se stejnými součiniteli samostatných oblouků publikovaných Macháčkem [2].
2. Rozsah studie, geometrické a materiálové charakteristiky
Studie se zabývá vnitřním obloukem válcových membránových konstrukcí s pěti ocelovými oblouky podle obr. 2. Parametrická studie zahrnuje reálné geometrické a materiálové parametry, různé tloušťky membrán, jejich různé předpětí a vliv tuhosti vnějších (čelních) oblouků.
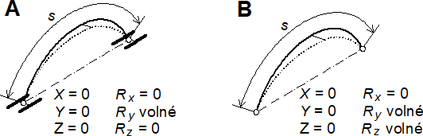
Sledované oblouky mají rozpětí L = 6 ÷ 20 [m], vzepětí H = L/10 ÷ L/2 (odtud plyne délka oblouku s) a jsou ve vzdálenosti B = 4 ÷ 10 [m]. Oblouky jsou ve své rovině uloženy kloubově, ze své roviny jako vetknuté (A), popř. kloubové (B), viz obr. 3.
Průřez oblouků je z ocelových trubek nebo tyčí IPE. Materiál byl zaveden jednotně jako ocel S355 s modulem pružnosti E = 210 GPa. Průřezy oblouků pro jednotlivé geometrie byly navrženy pro samostatný oblouk (bez připojených membrán) a svislé zatížení 6 kN/m působící na délku oblouku (odpovídá zatížení 1 kN/m2 plochy membránové konstrukce při vzdálenosti oblouků B = 6 m). Návrh byl proveden podle Eurokódu EN 1993-1 s použitím vzpěrných délek oblouků podle [2] tak, aby byl průřez využit na 80 ÷ 90 %. Celkem bylo navrženo 40 průřezů trubek (ø 70×4,5 [mm] až ø 245×8 [mm]) a pro limitovanou studii 4 průřezy IPE (IPE120 až IPE160). Je však třeba poznamenat, že pro sledované cíle (stanovení vzpěrných délek oblouků podpírajících membrány) není velikost průřezů podstatná a pouze zajistí správný tvar oblouků při příslušné deformaci konstrukce řešené geometricky nelineární analýzou (3D GNIA) před použitím lineární bifurkační analýzy (LBA).
Pro membránu byla vybrána polyesterová tkanina proložená PVC a zalakovaná PVDF (Précontraint FERRARI® 702S). Pevnostní a deformační vlastnosti membrány byly podrobně popsány v Části 1 [1], včetně ortotropních charakteristik pro numerickou analýzu v programu SOFiSTiK. Pro obvodová lana mezi oblouky byla vybrána nerezová spirálová pramenná lana Carl Stahl I-SYS 1×61 (ø 20 mm, pevnost v tahu 1470 MPa, modul pružnosti E = 130 GPa).
3. Numerická analýza
3.1 Model konstrukce
V programu AutoCAD-SOFiCAD byly pro každou válcovou membránovou konstrukci vymodelovány dvojkloubové oblouky s vypočtenými geometrickými a průřezovými parametry. Vnější (čelní) oblouky poskytují pro membránu v základní části studie tuhou liniovou podporu a vliv poddajného uložení na různě tuhých čelech (viz poslední schéma v obr. 2) je vyšetřováno v odstavci 4.4. Mezi oblouky byla vložena obvodová lana ve směru tečných rovin v uložení oblouků s odhadnutým zakřivením B/10. Výjimkou jsou půlkruhové oblouky (H/L = 0,5), kde rovina lan byla zvolena ve sklonu 15° od svislé (obr. 4).

Obr. 4 Rovina obvodových kotevních lan
Počáteční membránová plocha byla vygenerována mezi oblouky a obvodová lana jako plocha s minimálním povrchem (obr. 5). Po exportu do programu SOFiSTiK byla membrána modelována s ortotropními parametry podle Galliota a Luchsingera a s reálnou tloušťkou membrány 0,7 mm. K řešení byla použita 3D GNIA (podrobnosti byly popsány v Části 1 [1]). Citlivostní studie volby sítě nelineárních membránových prvků MEMBRANE (čtyřúhelníky s nejdelší hranou 100, 250, 500, 1000 a 500 [mm] se zjemněním v rozích, obr. 5) vyústila v optimální dělení 250 mm pro konstrukce s rozpětím L < 10 m a 500 mm pro rozpětí do 20 m, vždy bez zjemnění v rozích (Svoboda [3]). Oblouky byly modelovány jednotně s nelineárními prvky BEAM délky 100 mm.
Obr. 5 Studie citlivosti velikosti membránových prvků: a) 100 mm, b) 500 mm, c) 500 mm se zjemněním v rozích na 100 mm, d) 1000 mm
3.2 Předpětí a zatížení membránové konstrukce
Předpětí bylo do konstrukce vneseno stejně jako v Části 1 [1]. V membránách bylo zavedeno rovnoměrné předpětí přímo v lokálních osách konečných prvků o velikosti 5 kN/m (ve vyznačené části studie též 10 kN/m). V obvodových lanech bylo pro každý případ zavedeno předpětí podle vztahu (1) uvedeného v Části 1 [1]. Předpětí bylo vneseno do konstrukce ve 20 přírůstcích a výsledný deformovaný stav dává výchozí geometrii pro analýzu pod zatížením (viz obr. 6).
Daná membránová konstrukce (s reálnými průřezy oblouků) byla vyšetřována ve 3D GNIA v parametrické studii pod rovnoměrným svislým zatížením 1 kN/m2 působícím na plochu membrán. Zatížení bylo aplikováno ve 20 přírůstcích, v každém pro 50 akcelerovaných iterací mN-R (metoda arc-length). Výsledkem byla finální napjatost a deformovaná plocha membrán a oblouků, která byla následně použita pro stabilitní analýzu konstrukce.
4. Parametrická studie stability podpěrných oblouků
4.1 Součinitele vzpěrných (kritických) délek vnitřních oblouků
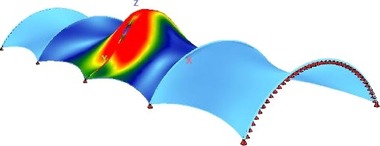
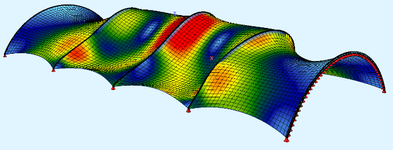
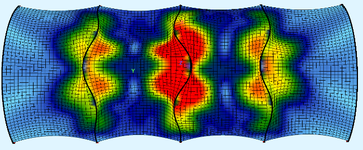
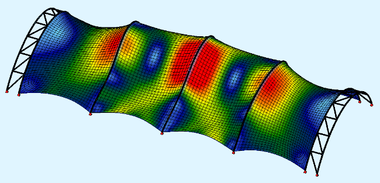
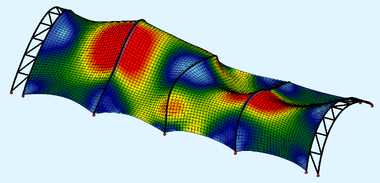
Pomocí lineární bifurkační analýzy (3D LBA) kompletní membránové konstrukce pod daným zatížením (tj. pouze od předpětí nebo konstrukce předpjaté a zatížené vnějším zatížením) lze stanovit nekonečné množství kritických zatížení a jim příslušných tvarů vybočení. Podpěrné oblouky vybočují při ztrátě stability v různém počtu „půlvln“ ve své rovině (ny) nebo ze své roviny (nz). Pro návrh jsou ve studii sledována pouze nejnižší kritická zatížení a odpovídající tvary vybočení. Na obr. 7 je pro ilustraci ukázáno vybočení v rovině oblouků (ke zvýraznění pouze pro liniové zatížení středního oblouku), obdobně na obr. 8 vybočení z roviny oblouků.
Obr. 7 Vybočení v rovině oblouku (vlevo se dvěma půlvlnami ny = 2, vpravo se třemi půlvlnami ny = 3)
Obr. 8 Vybočení z roviny oblouku v půdorysu (vlevo se dvěma půlvlnami nz = 2, vpravo se třemi půlvlnami nz = 3)
Vzpěrné délky oblouků scr jsou potom dány délkou „základního“ Eulerova kloubově uloženého prutu se stejným kritickým zatížením a platí (viz podrobně [2]):
kde je
- s
- délka oblouku (viz obr. 3),
- βcr
- součinitel vzpěrné délky oblouku,
- NE,v
- kritické zatížení „základního“ Eulerova prutu, avšak s proměnnou osovou silou po jeho délce,
- NE
- kritické zatížení Eulerova prutu s konstantní osovou silou,
- Ncr
- příslušné nejnižší kritické zatížení oblouku,
- αcr
- kritický násobitel pro dané zatížení,
- Nmax
- nejvyšší hodnota proměnné normálové síly (v patě vyšetřovaných oblouků),
- δi
- redukční součinitel Eulerovy síly pro prut s proměnnou osovou silou.
Eulerova kritická síla plyne ze známého vztahu:
kde tuhost EI se stanoví k ose kolmé k rovině (EIy pro vybočení v rovině oblouku, EIz pro vybočení z roviny oblouku).
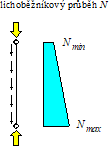
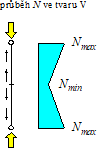
Obr. 9 Průběh normálové síly při odvození součinitele δi
Pro redukční součinitele δi byly podle proměnného průběhu síly odvozeny vztahy (obr. 9, [2]):
1) Pro lichoběžníkový průběh normálové síly:
2) Pro průběh normálové síly ve tvaru V:
Z průběhu normálových sil v obloucích předpjatých a zatížených membránových konstrukcí ve 3D GNIA byly stanoveny součinitele δi. V souladu s průběhem normálové síly v dané půlvlně byl při vybočení ve dvou půlvlnách v délce oblouku s použit součinitel δ1 podle vztahu (4), s jednou půlvlnou v délce oblouku součinitel δ2 podle (5) a při třech půlvlnách δ3 podle (4). Potřebnou odmocninu součinitelů pro různé vztažné poměry H/L uvádí Tab. 1.
| √δi | H/L = 0,1 | H/L = 0,2 | H/L = 0,3 | H/L = 0,4 | H/L = 0,5 |
|---|---|---|---|---|---|
| √δ1 | 0,98 | 0,94 | 0,90 | 0,86 | 0,83 |
| √δ2 | 0,99 | 0,96 | 0,94 | 0,91 | 0,90 |
| √δ3 | 0,99 | 0,96 | 0,93 | 0,91 | 0,89 |
V následující parametrické studii jsou uváděny součinitele vzpěrných (kritických) délek pouze pro oblouky membránových konstrukcí při zatížení předpětím a současně svislým rovnoměrným zatížením na plochu membrány (jak známo, kritické zatížení závisí na tvaru zatížení [2]). Součinitele pro samotné předpětí byly též stanoveny (viz [3]) a jsou o 2 ÷ 9 % vyšší. Nicméně tyto hodnoty nejsou pro konečný návrh konstrukce relevantní a nejsou proto uváděny.
4.2 Součinitele vzpěrných (kritických) délek vnitřních trubkových oblouků pro dokonale tuhé čelní oblouky
Grafické vyjádření součinitelů pro vybočení v rovině i z roviny oblouků je pro všechny poměry H/L uvedeno v následujících grafech. Protože hlavním cílem je vyšetření stabilizace oblouků membránou, je pro srovnání vždy uveden též součinitel platný pro samostatný oblouk bez membrány podle [2].
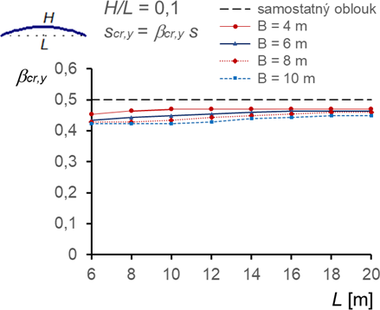
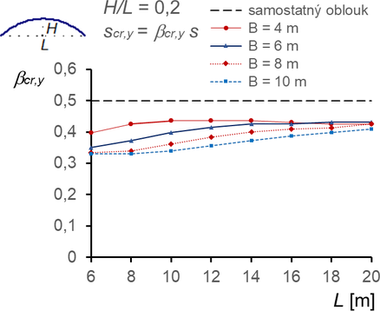
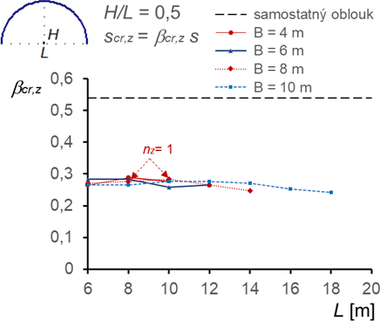
Ploché oblouky v membránové konstrukci (H/L ≤ 0,2) vybočují pro prvních pět kritických hodnot v rovině oblouku, k vybočení z roviny nedochází, a proto není uváděno (obr. 10). Ze srovnání se samostatným obloukem je stabilizace membránou zřetelnější pro větší vzdálenosti oblouků B a krátká rozpětí L, ale není výrazná. Ztráta stability prolomením u těchto oblouků nehrozí (viz Eurokód [4]).
Obr. 10 Součinitele vzpěrné délky βcr,y pro vybočení v rovině oblouků (vybočení se dvěma půlvlnami, ny = 2)
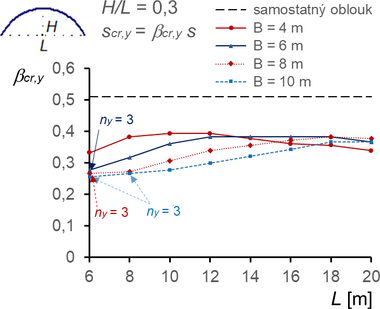
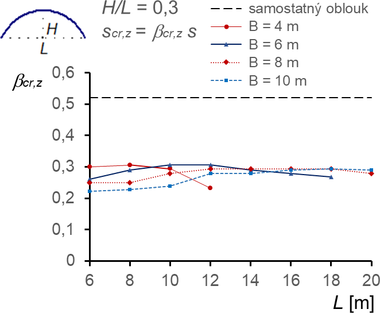
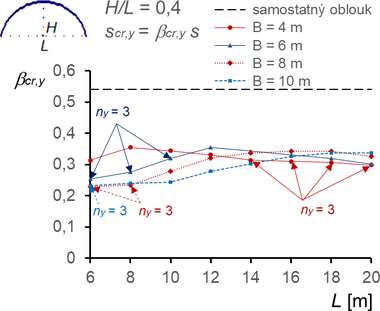
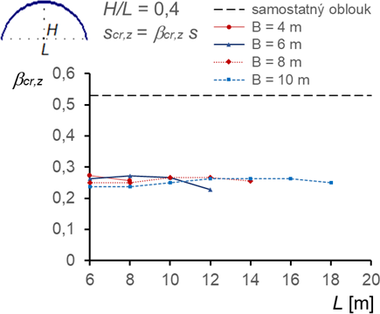
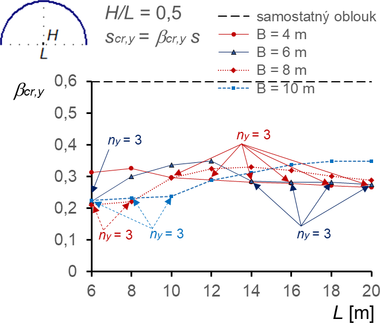
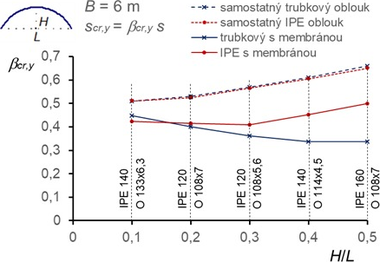
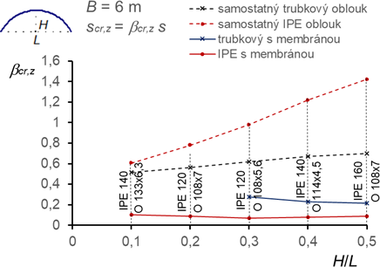
Konstrukce s větším poměrem (H/L ≥ 3) však vykazují výrazný stabilizační účinek membrány, a to jak pro vybočení v rovině, tak z roviny podpěrných oblouků (obr. 11, 12, 13). V rovině vybočují oblouky pokryté membránou se dvěma nebo třemi půlvlnami, z roviny se dvěma půlvlnami (výjimečně u vysokých oblouků s jednou půlvlnou).
Obr. 11 Součinitele vzpěrné délky βcr,y pro vybočení v rovině oblouků (vybočení se dvěma půlvlnami, ny = 2, nebo označené se třemi půlvlnami, ny = 3) a součinitele βcr,z pro vybočení z roviny oblouků (vybočení se dvěma půlvlnami nz = 2)
Obr. 12 Součinitele vzpěrné délky βcr,y pro vybočení v rovině oblouků (vybočení se dvěma půlvlnami, ny = 2, nebo označené se třemi půlvlnami, ny = 3) a součinitele βcr,z pro vybočení z roviny oblouků (vybočení se dvěma půlvlnami nz = 2)
Obr. 13 Součinitele vzpěrné délky βcr,y pro vybočení v rovině oblouků (vybočení se dvěma půlvlnami, ny = 2, nebo označené s třemi půlvlnami, ny = 3) a součinitele βcr,z pro vybočení z roviny oblouků (vybočení se dvěma půlvlnami nz = 2, nebo označené s jednou půlvlnou, nz = 1)
Obdobná studie s okrajovými podmínkami v uložení oblouků podle označení B (obr. 3) ukázala, že v případě ztužení membránou se kritická zatížení (a tedy i vzpěrné délky) od případu A neliší. Tento poznatek se liší od studie samostatných oblouků ([2]), kde kritická zatížení pro případ B jsou výrazně nižší (a tedy součinitele vzpěrných délek výrazně vyšší).
4.3 Součinitele vzpěrných (kritických) délek vnitřních trubkových oblouků pro vyšší předpětí a větší tloušťku membrán
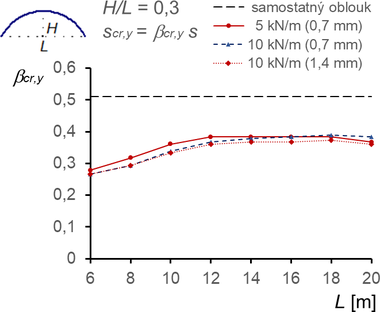
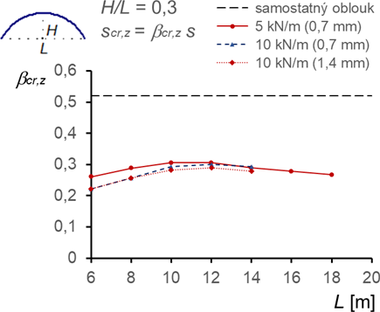
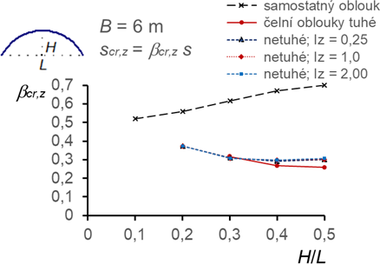
Význam velikosti předpětí a tloušťky membrán byl vyšetřován pouze pro omezený počet případů a konstrukce s oblouky s poměrem H/L = 0,3 se vzdáleností oblouků B = 6 m. Výsledky pro konstrukci s dvojnásobným předpětím 10 kN/m (a rovnoměrným svislým zatížením) a dvojnásobnou tloušťkou membrán pouze nepatrně ovlivnily hodnotu součinitele vzpěrné délky, obr. 14.
Obr. 14 Součinitele vzpěrných délek βcr,y a βcr,z pro konstrukce s různým předpětím a různou tloušťkou membrán
4.4 Součinitele vzpěrných (kritických) délek vnitřních oblouků s průřezem IPE
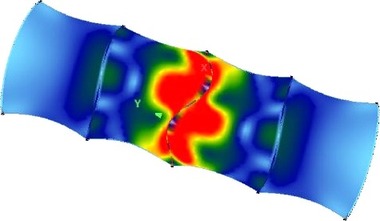
Jak ukázala studie samostatných oblouků [2], součinitele vzpěrných délek oblouků pro vybočení z roviny oblouku výrazně ovlivňuje tvar průřezu (resp. poměr momentu setrvačnosti k měkké ose vůči momentu setrvačnosti v prostém kroucení Iz/IT). V rámci studie válcové membránové konstrukce byla proto provedena analýza také s oblouky mající průřez IPE. Vyšetřována byla konstrukce s rozpětím L = 10 m, vzdáleností oblouků B = 6 m, obousměrným předpětím 5 kN/m, svislým zatížením na plochu membrán 1 kN/m2 a všechny poměry H/L = 0,1 ÷ 0,5. Průřezy oblouků z válcovaných IPE byly navrženy podle ČSN EN 1993-1-1, obdobně jako trubky v kapitole 2. Příklad vybočení konstrukce s poměrem H/L = 0,3 je ukázán na obr. 15. V rovině vybočil střední oblouk se dvěma půlvlnami (ny = 2), z roviny symetricky se třemi půlvlnami (nz = 3). Ploché oblouky (H/L ≤ 0,2) vybočovaly z roviny oblouků dokonce se čtyřmi půlvlnami (nz = 4).
Obr. 15 Vybočení konstrukce s oblouky z profilů IPE: v rovině oblouků (vlevo) a z roviny oblouků (vpravo)
Součinitele vzpěrných délek z celé studie jsou ukázány na obr. 16. Součinitele pro vybočení v rovině IPE oblouků ny jsou vesměs výrazně vyšší než pro trubky, což souvisí s malou tuhostí z roviny IPE oblouků (ve směru membrány), vybočení z roviny v mnoha půlvlnách a velmi nízkém součiniteli vzpěrných délek nz.
Obr. 16 Porovnání součinitelů vzpěrných délek βcr,y a βcr,z pro konstrukce s oblouky z trubek a profilů IPE (rozpětí L = 10 m)
4.5 Součinitele vzpěrných (kritických) délek vnitřních trubkových oblouků pro poddajné čelní oblouky
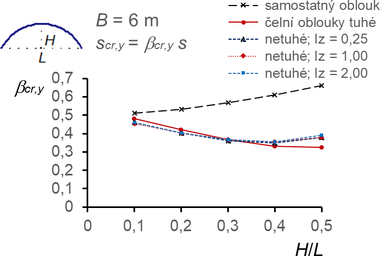
Stabilizace vnitřních oblouků membránou napjatou přes řadu oblouků od tuhých čelních oblouků vyvolává přirozeně otázku, nakolik poddajnost čelních oblouků (zejména z roviny oblouků) tuto stabilitu ovlivňuje.
Byla proto provedena orientační studie pro konstrukci s rozpětím L = 10 m, vzdáleností oblouků B = 6 m, poměrem vzepětí k rozpětí H/L = 0,1 ÷ 0,5, s předpětím 5 kN/m a svislým zatížením 1 kN/m2 na plochu membrán jako u základní studie s tuhými čelními oblouky. Čelní oblouky musejí nutně přenést kromě stejného zatížení jako střední oblouky též účinky předpětí membrán, takže jejich příčná tuhost musí být zvýšená. Ve studii byly proto zavedeny čelní oblouky jako zdvojené, ve třech různých vzdálenostech (0,5; 1,0; 1,4 [m]) a s příhradovým ztužením, obr. 17. Tomu podle Steinerovy věty odpovídají poměry momentů setrvačnosti průřezu Iz = 0,25; 1,0; 2,0.
Příčná tuhost příhradových čelních oblouků byla stanovena podle vztahu:
kde je
- F
- vodorovná síla [kN] působící ve vrcholu oblouku (F = 10 kN),
- s
- délka oblouku [m],
- δ
- vodorovný průhyb ve vrcholu příhradového oblouku [m].
Tato tuhost tedy záleží na momentu setrvačnosti průřezu Iz a poměru H/L. Pro sledované tři případy a různé poměry H/L je tuhost k = 15,9 ÷ 1476,0 [kN/m2]. Výsledky studie jsou uvedeny na obr. 18 a ukazují, že vliv poddajnosti čelních oblouků, pokud jsou schopné přenést předpětí a další zatížení, je zanedbatelný. Největší stabilizační účinek vykazují oblouky s poměrem H/L ≈ 0,4. Pro ploché konstrukce s poměrem H/L = 0,1 se kritické zatížení pro vybočení z roviny oblouků mezi prvními pěti tvary vybočení nevyskytovalo.
Obr. 18 Součinitele vzpěrných délek βcr,y a βcr,z pro konstrukce s čelními oblouky tuhými a poddajnými (rozpětí L = 10 m)
Příklad vybočení oblouků konstrukce s poměrem H/L = 0,3, střední hodnotou vzdáleností čelních oblouků 1 m a normálovou silou ve středním oblouku Nmax = 54,4 kN ukazuje obr. 19. V rovině všechny oblouky vybočují se dvěma půlvlnami (ny = 2). Z roviny vybočuje střední oblouk rovněž se dvěma půlvlnami (nz = 2), avšak sousední oblouky vybočují asymetricky ve svých rovinách.
Obr. 19 Vybočení v rovině oblouků pro αcr,y = 5,58 (vlevo) a vybočení z roviny oblouků pro αcr,z = 7,38 (vpravo)
5. Závěr
Článek uvádí vzpěrné délky podpěrných oblouků válcové membránové konstrukce. Pokrývá realistické geometrie (rozpětí oblouků L = 6 ÷ 20 [m], vzdálenosti oblouků B = 4 ÷ 10 [m], vzepětí k rozpětí H/L = L/10 ÷ L/2, potřebný průřez oblouků z trubek nebo profilů IPE), dva typy uložení oblouků a různé tuhosti čel membránové konstrukce, ortotropní parametry textilní membrány s obousměrným předpětím 5 kN/m nebo 10 kN/m a dalším rovnoměrným svislým zatížením na plochu membrán. Konstrukce byla analyzována ve 3D GNA k získání deformovaného tvaru při daném zatížení a následně ve 3D LBA k získání kritického zatížení.
Výsledky jsou ve formě součinitelů vzpěrných (kritických) délek vnitřních oblouků pro vybočení v rovině (βcr,y) a z roviny oblouků (βcr,z), které jsou vztaženy v obou případech k celkové délce oblouku s. Tyto výsledky lze použít k usnadnění separátního posouzení podpěrných ocelových oblouků membránových konstrukcí.
Hlavní poznatky:
- Grafické výstupy pro ploché oblouky (H/L ≤ 0,2, obr. 10) ukazují, že redukce součinitelů vzpěrných délek vůči obloukům bez membrány pro vybočení v rovině oblouků je malá (~ 8 ÷ 34 %), zejména pro poměr H/L = 0,1 a velká rozpětí oblouků. Z roviny jsou tyto oblouky účinně stabilizovány membránou a nevybočují.
- Redukce součinitelů vzpěrných délek membránou pro oblouky s poměrem H/L ≥ 0,3 (obr. 11 ÷ 13) je vlivem membrány výrazná (vesměs až 50 %), a to jak pro vybočení v rovině oblouků, tak ještě výrazněji z roviny oblouků.
- Studie prokázala nevýrazný vliv tloušťky membrány i velikosti předpětí v membráně na tyto redukce (obr. 14).
- Oblouky z otevřených průřezů IPE vybočují v membránové konstrukci jinak než oblouky uzavřené trubkové. Oblouky vybočují ze své roviny (ve směru měkké osy průřezu, tj. ve směru membrány) ve více půlvlnách. Součinitele vzpěrných délek z roviny oblouků IPE jsou proto nižší než u stejných oblouků z trubek a mnohonásobně nižší než u oblouků bez membrán (obr. 16). Pro vybočení v rovině oblouků jsou součinitele naopak vesměs vyšší než u stejných oblouků z trubek, avšak podstatně nižší než u samostatných oblouků bez membrány.
- Studie poddajnosti čelních oblouků membránové válcové konstrukce ukázala, že reálná poddajnost čel jen nepatrně ovlivňuje velikost součinitelů vzpěrných délek oblouků jak v rovině, tak z roviny oblouků (obr. 18). Požadavkem ovšem je dostatečná tuhost a dimenze čel pro přenos předpětí v membránách a dalšího zatížení čel.
6. Literatura
- Macháček, J. a Svoboda, O.: Ocelové oblouky stabilizované membránami. Část 1: Experimenty a analýza. TZB-info, 13 s.
- Macháček, J.: Stabilita ocelových kruhových oblouků. TZB-info, ocelové konstrukce, 8.3.2021, 11 stran, https://stavba.tzb-info.cz/ocelove-konstrukce/21953-stabilita-ocelovych-kruhovych-oblouku
- Svoboda, O.: Stabilizace ocelového oblouku nekovovou membránou. Ph.D. disertace, FSv ČVUT, 2019, 149 s.
- ČSN EN 1993-2: Navrhování ocelových konstrukcí – Část 2: Ocelové mosty. ČNI 2007, 103 s.
Poděkování
Článek a související výzkum vznikl za podpory grantu SGS19/150/OHK1/3T/11.
Článek navazuje na první část věnovanou experimentální a numerické analýze konkrétní konstrukce oblouku s membránou, jejímž výsledkem bylo vytvoření numerického modelu a jeho ověření a porovnání s výsledky experimentů. Druhá část se věnuje parametrické studii zaměřené na stanovení vzpěrných délek oblouků stabilizovaných membránami při vybočení v rovině a z roviny oblouku a jejich porovnání se vzpěrnými délkami samostatných oblouků. Studie se zabývá vnitřním obloukem válcových membránových konstrukcí s pěti ocelovými oblouky s cílem ověřit stabilizující vliv membrány na jeho vzpěrnou délku, přičemž do modelu byly zavedeny reálné geometrické a materiálové charakteristiky a je sledován vliv tloušťky membrány, jejího předpětí a tuhosti čelních oblouků na vzpěrnou délku vnitřního oblouku. Článek poskytuje nové a prakticky použitelné informace o stabilizujícím účinku membrán na vzpěrnou délku oblouku pro vybočení v rovině i z roviny oblouku. V článku jsou uvedeny výsledky parametrické studie provedené pro určitý typ konstrukce tvořené ocelovými oblouky stabilizovanými membránou, nicméně dosažené výsledky a přístup k řešení mohou být vhodně aplikovány pro rozsáhlejší parametrické studie dalších konstrukcí tohoto typu, např. s jinými hodnotami parametrů ovlivňujících stabilitu konstrukce. Předložený článek doporučuji k publikaci.
The article is a follow-up to the Part 1: Experiments and analysis [1], in which a numerical model dealing with membrane structures supported by steel arches in software SOFiSTiK using 3D GNIA and 3D GNA is introduced and validated. This part investigates parametrically stability and buckling of arches of a barrel type membrane structure using linear buckling analysis (3D LBA). The in-plane and out of plane buckling factors of the arches for a vast spectrum of practical geometrical parameters of the structure, membrane pretension and support conditions of the arches and membrane frontiers are presented and confronted with the ones belonging to the arches alone.