Stabilita ocelových kruhových oblouků
Článek analyzuje stabilitu dvojkloubových kruhových oblouků pro různá rovnoměrná zatížení (svislá na půdorys oblouku, svislá na délku oblouku a radiální na osu oblouku). Ke stanovení kritického zatížení se používá lineární bifurkační analýza a následně jsou určeny součinitele vzpěrné délky oblouků. S výjimkou radiálního zatížení je nutné vzhledem k proměnné normálové síle v obloucích uvažovat vztažný Eulerův základní prut se stejným průběhem proměnné osové síly. Analýza byla provedena pro různé okrajové podmínky oblouků v podporách. Studie zahrnovala oblouky s uzavřenými i otevřenými průřezy a prokázala významný vliv tvaru průřezu na vzpěrné délky pro vybočení z roviny oblouků. Výsledkem jsou tabulky pro korektní součinitele vzpěrných délek.
1. Úvod
Při návrhu ocelových oblouků podle Eurokódu (ČSN EN 1993-1-1/2005, kap. 5.2 „Globální analýza“) lze v pružné oblasti použít geometricky nelineární analýzu pro imperfektní oblouk (GNIA, popř. zjednodušení ve formě teorie 2. řádu) a posouzení provést na příslušné prosté vnitřní síly. Další možností je řešení ideálního oblouku lineární analýzou (LA) ve spojení s lineární bifurkační analýzou (LBA), které vedou k posouzení stability pomocí kritických sil (popř. kritických momentů) a následný posudek provést se součiniteli vzpěrnosti, popř. klopení.
Teoretická řešení stability oblouků předložili již v první polovině 20. století Timoshenko a Gere [1], v padesátých létech podrobněji v obecné teorii stability Vlasov [2]. Následné studie obsahují podrobná řešení pro nejrůznější parametry oblouků (např. Ziemian [3]) a výsledky byly převzaty do norem, včetně Eurokódů. Návrh oblouků s využitím plastické únosnosti průřezů publikovali Verstappen a kol. [4]. V posledním období bylo vyšetřováno zejména chování velmi plochých oblouků s možnou ztrátou stability prolomením pod zatížením (Pi a Trahair [5], Bradford a Pi [6] a Pi a kol. [7]).
Předkládaná studie se zabývá obvyklým případem kruhového oblouku s kloubovým uložením (tzv. dvojkloubový oblouk). Vyšetřování je zaměřeno na stanovení vzpěrných délek těchto oblouků pomocí lineární bifurkační analýzy (LBA). V běžné literatuře a v normách (např. mostní normě ČSN EN 1993-2/2007) jsou uváděny hodnoty vzpěrných (kritických) délek pro vybočení v rovině a z roviny oblouků. Jak bude ukázáno, tyto hodnoty však nejsou příliš spolehlivé, zejména pro vybočení z roviny oblouků.
2. Stabilitní analýza kruhových oblouků
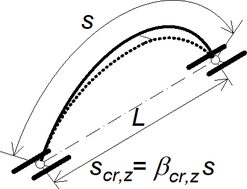
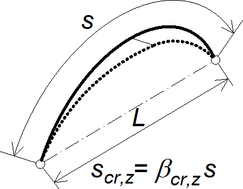
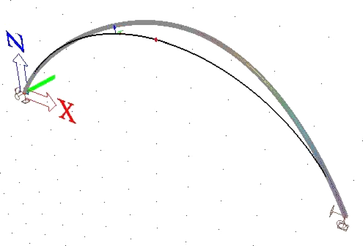
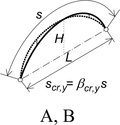
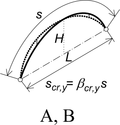
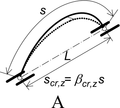
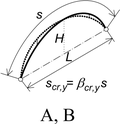
Pro vyšetřování stability ideálních oblouků ve 3D byl použit program SCIA Engineer (verze 20.0). Oblouky byly výhradně kruhové, dvojkloubové a zatížené svislým rovnoměrným zatížením na půdorys oblouku nebo na délku oblouku a dále též radiálním zatížením na osu oblouku. Průřezy oblouků byly uzavřené (tenkostěnné trubky) i otevřené (profily IPE a HEB). Geometrie oblouků pokrývá poměry H/L (výška k rozpětí) od 0,1 do 0,5 (obr. 1).
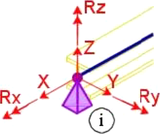
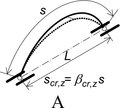
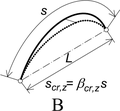
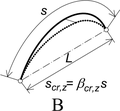
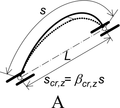
Okrajové podmínky v podporách jsou uvedeny na obr. 2. Případ A odpovídá běžnému uspořádání, s vetknutím pro vybočení z roviny oblouků (vidlicové nebo válcové uložení, vytvářející „balkonový nosník“). Případ B též umožňuje stabilitní řešení, avšak oblouk již nepřenáší příčné zatížení. Stabilitní řešení s dalším uvolněním (volným natočením kolem osy x) již není možné.
Posun v podporách:
- X
- zabráněn
- Y
- zabráněn
- Z
- zabráněn
Natočení v podporách:
- Rx
- zabráněno
- Ry
- volné
- Rz
- zabráněno
Posun v podporách:
- X
- zabráněn
- Y
- zabráněn
- Z
- zabráněn
Natočení v podporách:
- Rx
- zabráněno
- Ry
- volné
- Rz
- volné
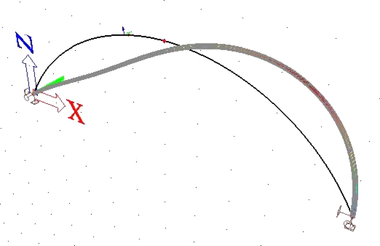
Ze stabilitní analýzy ve 3D byla získána nejnižší kritická zatížení pro vybočení v rovině a z roviny oblouků (ztrátu stability kroucením nebo s vlivem kroucení program neumožňuje). Zatímco v rovině oblouk vybočuje ve dvou polovlnách, z roviny oblouku v jedné polovlně (příklad pro oblouk s poměrem H/L = 0,3 je na obr. 3).
Vzpěrná (kritická) délka oblouku scr je potom dána délkou „základního“ Eulerova kloubově uloženého prutu se stejným kritickým zatížením a součinitel kritické délky βcr plyne ze vztahu:
kde Ncr je příslušné nejnižší kritické zatížení oblouku a Eulerova kritická síla vztažného tlačeného prutu NE je
V této analýze je vzpěrná délka oblouku scr vztažena k celé délce oblouku s jak pro vybočení v rovině, tak i z roviny oblouku (naproti tomu některé publikace a normy, např. mostní Eurokód ČSN EN 1993-2/2007, vztahují vzpěrnou délku pro vybočení v rovině k poloviční délce oblouku s/2 a pro vybočení z roviny k půdorysnému průmětu celého oblouku L). Ve vztahu (2) se zavede pro vybočení v rovině oblouku moment setrvačnosti průřezu k hlavní ose (Iy) a pro vybočení z roviny moment setrvačnosti průřezu k měkké ose (Iz).
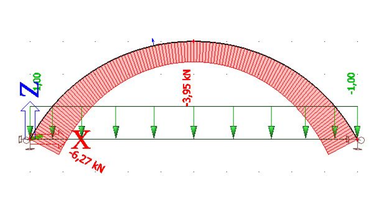
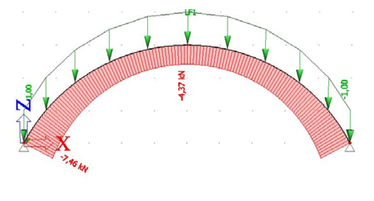
Kritické zatížení oblouku je dáno násobkem zadaného zatížení a tomuto násobku odpovídají i vnitřní síly v oblouku. Normálová síla v oblouku je však pro svislé zatížení proměnná, nejmenší je ve vrcholu a největší v podpoře oblouku (např. pro oblouk s poměrem H/L = 0,3 a zatížený jednotkovým svislým zatížením na půdorys oblouku nebo jednotkovým svislým zatížením po délce oblouku je vykreslena na obr. 4).
Obr. 4 Průběh normálové síly na oblouku s poměrem H/L = 0,3 a rozpětím 10 m pro jednotkové rovnoměrné svislé zatížení na půdorys oblouku (vlevo, poměr Nmin/Nmax = 0,630) a pro jednotkové rovnoměrné svislé zatížení na délku oblouku (vpravo, poměr Nmin/Nmax = 0,586)
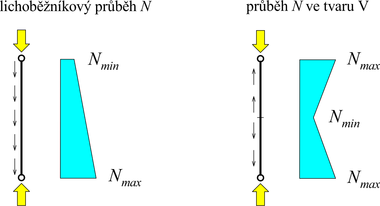
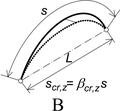
Pro stanovení součinitele vzpěrné (kritické) délky βcr je proto nutné pro tyto případy použít rovněž vztažný „základní“ Eulerův prut kloubově podepřený s proměnnou osovou silou. Průběh osové síly v oblouku mezi vrcholem a podporou je zhruba lineární. Obdobně byla proto provedena analýza kritického zatížení „základního“ prutu s proměnnou osovou silou podle obr. 5. Při vybočení oblouku v rovině (dvě polovlny) se jedná o lichoběžníkový průběh normálové síly (Nmin ve vrcholu a Nmax v podpoře), zatímco při vybočení oblouku z roviny (jedna polovlna) je průběh dané osové síly zhruba ve tvaru V (Nmax v podporách a Nmin ve vrcholu), se zanedbáním „hladkosti“ průběhu uprostřed délky.
Kritické zatížení vztažného „základního“ prutu s proměnným zatížením NE,v je vyšší než kritické zatížení téhož prutu s konstantním zatížením NE (s obdélníkovým průběhem normálové síly). Numerické řešení uvedených případů (provedené parametricky v programu SCIA Engineer) lze ve výsledku popsat následovně:
- Pro lichoběžníkový průběh normálové síly:
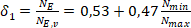 (3)
(3)
pro 0 ≤ Nmin ≤ Nmax
- Pro průběh normálové síly ve tvaru V:
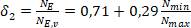 (4)
(4)
pro 0 ≤ Nmin ≤ Nmax
Po záměně Eulerovy kritické síly NE za NE,v v rovnici (1) lze tedy psát:
kde Ncr je kritické zatížení prutu s proměnnou osovou silou (dané součinem kritického násobitele αcr a maximální normálovou silou v prutu), δi součinitel platný pro příslušný průběh normálové síly a βmax je součinitel vzpěrné (kritické) délky stanovený pro maximální osovou sílu v prutu.
3. Vzpěrné délky kruhových oblouků pod rovnoměrným svislým zatížením působícím na půdorys
Shrnutí výsledků pro obě podmínky uložení v podporách jsou uvedeny v tabulkách 1 a 2. Analýza zahrnovala celou řadu průřezů uzavřených (tenkostěnných trubek 108×6,3 až 457×20,0) a otevřených (válcovaných průřezů IPE120 až IPE450 a širokopřírubových HEB120 až HEB450).
Součinitele vzpěrných (kritických) délek jsou vždy vztaženy k celé délce oblouku podle rovnice (1) a zahrnují vliv proměnné normálové síly pro svislé rovnoměrné zatížení oblouku působící na půdorys oblouku podle rovnice (5). Po tomto převedení na Eulerův prut se stejnou kritickou silou se tedy pro následné posouzení průřezu uvažuje maximální normálová síla v podporách.
V tabulce 1 je uveden součinitel vzpěrných (kritických) délek pro vybočení v rovině oblouku βcr,y, který je zhruba stejný pro všechny průřezy oblouků. Pro porovnání je uveden i součinitel podle mostního Eurokódu ČSN EN 1993-2 (po přepočtu na celou délku oblouku).
V tabulce 2 je uveden součinitel vzpěrných délek pro vybočení z roviny oblouku βcr,z, který ale velmi závisí na poměru momentu setrvačnosti pro měkkou osu k momentu v prostém kroucení (Iz/IT). Pro porovnání je opět uveden i součinitel podle mostního Eurokódu ČSN EN 1993-2 (po přepočtu na celou délku oblouku), který však nerespektuje poměr tuhostí a není tedy správný (podmínky v podporách typu B norma neuvádí).
4. Vzpěrné délky kruhových oblouků pod rovnoměrným svislým zatížením působícím na délku oblouku
Shrnutí výsledků parametrické studie je pro toto zatížení (spíše neobvyklé) uvedeno obdobně pro vybočení v rovině oblouku v tabulce 3 a pro vybočení z roviny oblouku v tabulce 4. Hodnoty Eurokódu nerozlišují typ svislého zatížení a jsou proto stejné jako v předchozích tabulkách.
5. Vzpěrné délky kruhových oblouků pod radiálním zatížením
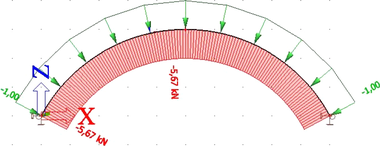
Obr. 6 Průběh normálové síly na oblouku s poměrem H/L = 0,3 a rozpětí 10 m pro jednotkové rovnoměrné radiální zatížení působící na osu oblouku (poměr Nmin/Nmax = 1,0)
Shrnutí výsledků parametrické studie pro toto zatížení (viz obr. 6) a vybočení v rovině oblouku je uvedeno v tabulce 5, pro vybočení z roviny oblouku v tabulce 6. Eurokód pro toto zatížení hodnoty vzpěrných délek pro vybočení v rovině neuvádí, pro vybočení z roviny poskytuje Timoshenkův vzorec.
Průběh osové normálové síly v oblouku je zde konstantní, takže pro vyhodnocení součinitele vzpěrné (kritické) délky se zavádí běžná Eulerova síla NE podle vztahu (2).
4. Závěr
Analýza kruhových oblouků pod rovnoměrným zatížením výrazně zpřesnila hodnoty součinitelů vzpěrných délek uváděných v literatuře i normách. Uvedené hodnoty součinitelů pro vybočení v rovině i z roviny oblouků se vztahují k celé délce oblouků, takže porovnávací hodnoty z mostního Eurokódu (ČSN EN 1993-2/2007) byly přepočteny na tuto stejnou vztažnou délku.
Studie ukázala, že pro vybočení oblouků z roviny jsou důležité podmínky uložení v podporách (vetknutí (A) nebo možnost natočení z roviny oblouku (B)) a zejména potom poměr tuhostí průřezu k měkké ose a v kroucení. Vzpěrné délky „otevřených“ průřezů (tvaru I) jsou potom výrazně vyšší než u průřezů uzavřených (trubek). Tyto významné rozdíly současné normy ani literatura neuvádějí. Dalším důležitým poznatkem je potřeba zahrnout do analýzy vliv případné proměnné normálové síly v obloucích a při posouzení odpovídající průřez ekvivalentního Eulerova prutu (pro hodnoty v této studii je to průřez v podporách, s maximální normálovou silou).
Jak známo z řešení stability konstrukcí, významný je i vliv tvaru zatížení. V této studii jsou analyzována pouze rovnoměrná zatížení (svislé na půdorys oblouku, svislé na délku oblouku a radiální zatížení působící na osu oblouku). Pro nerovnoměrná zatížení lze očekávat příslušně odlišné součinitele vzpěrných délek.
5. Literatura
- Timoshenko, S. P. and Gere, J. M.: Theory of Elastic Stability. McGraw-Hill, 17th Printing, 1985, 541 s.
- Vlasov, V. Z.: Tenkostěnné pružné pruty. SNTL, 1962, 572 s.
- Ziemian, R. D.: Guide to stability design criteria for metal structures, 6th Edition, John Wiley & Sons, 2010, 1120 s.
- Verstappen, I., Snijder, H. H., Biljaard, F. S. K. and Steembergen, H. M. G. M.: Design rules for steel arches-in-plane stability. Journal of Constructional Steel Research, 1998, Vol. 46, No. 1-3, s. 125-126.
- Pi, Y. L.and Trahair, N. S.: Non-linear buckling and pstbuckling of elastic arches. Eng. Structures, 1998, Vol. 20, No. 7, s. 571-579.
- Bradford and Pi, Y. L.: Design of steel arches against in-plane stability. Advances in Steel Struct., Vol. I, 2002, Elsevier Science Ltd., 10 s.
- Pi, Y. L., Bradford, M. A. and Uy, B.: In-plane stability of arches. Intern. Journal of Solids and Structures, 2002, Vol. 39, No. 2, s. 105-125.
Poděkování
Článek a související výzkum vznikl za podpory grantu SGS19/150/OHK1/3T/11.
The article presents a stability analysis of circular arches under various uniform loadings (vertical to the arch plan, vertical to the arch length or radial to the arch axis). Linear bifurcation analysis resulted into critical loadings used for determination of the arches buckling length factors. With the exception of the radial loading the variable axial arch forces need to be taken into account also for the relative Euler basic strut. The analysis covers various boundary conditions of the arches in supports. The study embodies arches with both closed and open cross sections and proved the significant impact of the cross-sectional shape on out-of-plane buckling values. The article outcomes are tables with correct buckling length factors of arches.