Ocelové oblouky stabilizované membránami. Část 1: Experimenty a analýza
V článku se popisuje a analyzuje test modelu přístřešku s textilní membránou podpíraného trubkovým ocelovým obloukem. Cílem vyšetřování je prostorové chování podpěrného oblouku pro jeho návrh z hlediska stability. Testuje se rozdíl chování samostatného vetknutého oblouku oproti jeho chování v membránové konstrukci. Uvedena jsou vstupní data, postup předpínání a zatěžování a experimentální výsledky. Pro numerickou analýzu v programu SOFiSTiK byla použita pružnostní, geometricky nelineární analýza s imperfekcemi respektující ortotropní chování membrány. Úspěšná validace numerických výsledků podle testů umožňuje rozsáhlé numerické parametrické studie zaměřené na stabilitu oblouků válcových membránových konstrukcí v druhé části článku.
1. Úvod
Moderní tkané membránové konstrukce vynikají estetikou tvarů, jsou extrémně lehké, v současnosti snadno dostupné a využitelné pro dočasné i trvalé konstrukce. Materiál membrán lze volit z široké nabídky výrobců. Vhodnou volbou je jednovrstvá polyesterová tkanina (PES, PET) proložená vrstvami polymerů (PVC popř. PU, nebo akrylátovým či silikonovým polymerem, obvykle potažená fluoropolymerem PVDF) s trvanlivostí nejméně 20 let a umožňující spojování svařením nebo sešíváním (viz Précontraint FERRARI® [1], SATTLER PRO-TEX GmbH [2]). Poněkud dražší, nehořlavá a s trvanlivostí min. 35 let je skelná tkanina potažená PTFE (teflon) nebo silikonovou gumou, popř. oxidem titaničitým a spojuje se lepením. Drahým, avšak výborným materiálem je tkanina z expandovaných PTFE vláken potažená pružným fluoropolymerem (TENARA® [3]), s trvanlivostí min. 35 let. Jedná se o průsvitný materiál s možností skládání/ohýbání a spojovaný svařováním. V případě potřeby lze membrány i tepelně izolovat použitím materiálu Nanogel Aerogel™ vloženého mezi PTEF popř. PVC membrány (viz Tensotherm™ [4], s dalším povlakem akustickým nebo parozábranou), tvořící pružnou a průsvitnou deku s tloušťkou do 24 mm ukládanou do roštu. Pro méně náročné, dočasné membrány (s trvanlivostí do 10 let), lze použít též polyetylen s vysokou hustotou (HDPE) potažený polyetylenem s nízkou hustotou (LDPE), spojovaný sešíváním. K membránovým materiálům lze řadit i plastické fólie s tloušťkou 50÷500 μm používané zejména pro nafukovací polštáře, nejčastěji z ETFE (TEXLON®), popř. s horšími termomechanickými vlastnostmi z fluoroplastu THV.
Navrhování membránových konstrukcí a jejich podpůrných ocelových konstrukcí je dobře popsáno (viz Seidel [5], Jermoljev [6], Svoboda [7]). Výstižný postup uvedl v krocích Lewis [8]: a) Předběžný návrh tvaru zajišťující v celé oblasti membrány tahové napětí při montáži i zatížení, vyžadující ovšem dostatečné předpětí (základními tvary jsou hyperbolický paraboloid, kužel a membrány na obloucích). b) Výběr upevnění na okrajích (bodové nebo průběžné, tuhé nebo pružné) a příslušných periferních prvků (předpjatá lana, rámové konstrukce, kotvící body nebo lana). c) Hledání tvaru (form-finding proces), obvykle s použitím softwaru na bázi metody hustoty sil (force-density) nebo modernějších sofistikovaných metod (např. Čápová [9]). d) Analýza membránové konstrukce a podpůrné konstrukce pro dané předpětí (které ovlivňuje počáteční geometrii) a zatížení. Jednotlivé kroky návrhu jsou dobře popsány v bohaté literatuře (např. Foster a Mollaert [10], Wakefield [11]).
Vyšetřování konstrukcí s membránami v celé šíři vyžaduje geometricky a materiálově nelineární analýzu s uvažováním imperfekcí (GMNIA). Zatímco geometrická nelinearita a počáteční deformace zásadně ovlivňují stabilitu, napjatost a deformace konstrukce při předpínání i pod zatížením, materiálovou nelinearitu je nutné zvažovat z více hledisek. Materiál membrán je obecně nehomogenní, přinejmenším ortotropní (má jiné vlastnosti ve směrech osnovy a útku) a nelineární. Materiálovými modely se zabývá řada studií (např. Kato a kol. [12], Dinh a kol. [13], Pargana a Leitao [14] a další). Vhodný model navrhli Galliot a Luchsinger [15], který byl implementován do programu SOFiSTiK [16] a který je použit v tomto článku. Podle doporučení pracovní skupiny Tensinet Analysis & Materials [17] lze v běžném návrhu použít pro materiál pružnostní ortotropní lineární analýzu.
Chování membrán a podpůrné konstrukce nelze řešit separátně (viz Macháček a Jermoljev [18]). Kompletní statické řešení nabízejí speciální softwary, popř. obecné programy s doplňkovými moduly (např. Easy [19], ixCube/Rhino membrane [20], SOFiSTiK [21], NDN [22], RFEM [23]). Pro realizaci je nezbytné řešení optimalizace střihu a kompenzací tkaniny membrán (viz např. Gale a Lewis [24]) a vhodné řešení detailů (Seidel [5]). V ČR je řada velmi úspěšných realizací membránových konstrukcí a specialistů pro jejich navrhování (viz např. Archtex [25], Jermoljev [26], Janata a kol. [27]).
Tato studie se zaměřuje na stabilizační efekt membrán vzhledem k podpůrné konstrukci z ocelových oblouků. V první části (1: Experimenty a analýza) je popsán model membránové konstrukce pro zakrytí koncertního pódia, jeho provedení a testování v laboratoři Fakulty stavební ČVUT v Praze. Dále je uvedena numerická analýza pro statické řešení a validace tohoto řešení na výsledcích testů. V druhé části (2: Parametrické studie ocelových oblouků stabilizovaných membránami [28]) je analyzována stabilita oblouků podpírajících válcovou membránu s různými okrajovými podmínkami.
2. Laboratorní model
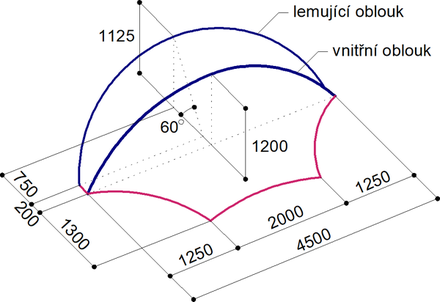
Návrh modelu vychází z typové řady Dome Stagecover [29] a reprezentuje přístřešek zhruba v měřítku 1:10. Konstrukce má dva ocelové trubkové oblouky pokryté textilní membránou, dolní okraje lanové, s kotevními deskami (obr. 1). Pro membránu byla použita polyesterová tkanina proložená PVC a zalakovaná PVDF (Précontraint FERRARI® 702S, s neprůsvitným povrchem a váhou 830 g/m2). Patentovaný výrobní postup zajišťuje víceméně stejné deformační vlastnosti membrány v obou směrech (osnovy i útku) a minimální dotvarování. Materiál byl podroben biaxiálním testům ve Stuttgartu [30], vedoucím v obou směrech k únosnosti při porušení Sult ≈ 56 kN/m, doporučenému zatížení Smax = Sult / 5 ≈ 11,2 kN/m a předpínání do P = Smax / 5 ≈ 2,2 kN/m. Vnitřní svislý ocelový oblouk má rozměry L/H = 4500×1200 [mm], zatímco vnější lemující oblouk má sklon 60°.
Obě ocelové trubky konstrukce byly vyrobeny z oceli S355J0 a za tepla ohnuty v dílně (JPB Kovovýroba Březenec - Jirkov) a v laboratoři přivařeny k ocelovým blokům pro dokonalé vetknutí. Vnitřní trubka má ø 26,9×3,2 [mm], poloměr R = 2709 mm a je předmětem stabilitního vyšetřování. Vnější lemující trubka má ø 88,9×3,2 [mm]. Z tahových zkoušek vzorků z obou trubek vyplynula průměrná mez kluzu fy = 475 MPa, pevnost fu = 595 MPa a tažnost 27,1 %. Modul pružnosti pro vyhodnocení zkoušek byl brán normovou hodnotou E = 210 MPa.
Přípoj membrány k obloukům je patrný z obr. 2. K vnějšímu oblouku je uchycena pomocí hliníkové upínací lišty s keder profilem, k vnitřnímu oblouku byly membrány navlečeny prostřednictvím vystříhaných kapes. Volný obvod membrány byl vyztužen ocelovými lanky ø 6 mm (7×7 lanka CarlStahl) protaženými kapsami membrán a ukončenými nalisovanými závitovými koncovkami. Předpětí membrán bylo dosaženo v ukotvení na nerezových platlích utahováním matic koncovek, částečně i mezi oblouky napínacími šrouby.
Vyšetřovaná vnitřní trubka byla vystrojena snímači (elektrickými potenciometry) pro přemístění ve svislém (V), vodorovném (H) a podélném (L) směru. V blízkosti podpor a ve vrcholu oblouku byly na trubku umístěny v podélném směru tenzometry (T) pro měření napětí (vždy na obou površích a na bocích trubky, k eliminaci napětí od ohybu). Po osazení membrán byly na jejich povrch mezi vrcholy oblouků osazeny čtyři dvojice vzájemně kolmých tenzometrů pro orientační zjištění napjatosti membrány. Zatížení bylo aplikováno na závěsy v sedmi bodech (P), viz obr. 3.
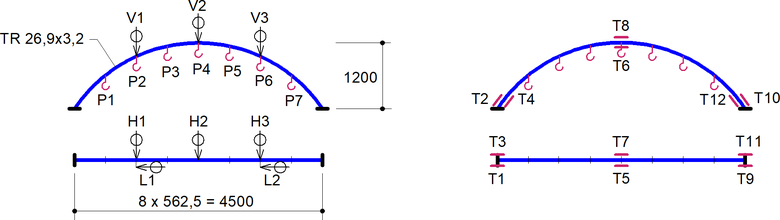
Obr. 3 Pohled a půdorys vnitřního oblouku. Umístění zatížení (P), snímačů přemístění (V, H, L) a tenzometrů (T)
2.1 Tvar membrán a jejich předpětí
Přepětí membrán odpovídající tvaru a střihu membrán s danými okrajovými podmínkami podle programu EASY [19] předpokládalo rovnoměrné předpětí přibližně P = 0,5 kN/m. Při montáži byla napínána obvodová lanka a membrána kontrolována vůči zvrásnění. Po dosažení žádaného stavu byly měřeny hodnoty napjatosti na povrchu membrány v okolí oblouků a zjištěno předpětí ve směru oblouků εx = 450 μm/m (tj. Pe ≈ 0,31 kN/m) a kolmo na oblouky εy = 140 μm/m (tj. Pe ≈ 0,10 kN/m).
2.2 Zatížení a postup měření
Experiment byl zaměřen výlučně na chování vnitřního oblouku a stabilizační efekt membrány. Napřed byl tedy vyšetřován samostatný oblouk a poté celá membránová konstrukce. Z rozdílu lze posoudit stabilizační vliv membrány na chování oblouku.
Zatížení bylo ve formě kalibrovaných váčků naplněných ocelovými broky, zavěšovaných v bodech P oblouku. Přírůstek v zatěžovacím kroku každého bodu byl zhruba 10 kg, následovalo odtížení a zatížení na vyšší stupeň. Zatížení bylo buď symetrické, nebo nesymetrické a bylo ukončeno při dosažení nadměrných deformací (u samostatného oblouku z jeho roviny při ⁓ 80 mm), nebo vysokou hodnotou napětí v uložení oblouku (u membránové konstrukce při dosažení až 287 MPa), obr. 4. Odečty hodnot elektrických potenciometrů (pro průhyby) a tenzometrů byly prováděny po ustálení hodnot (min. 40 s) a následně byly statisticky zpracovány (viz Svoboda [7]). Měření počátečních deformací ve vodorovném směru (potenciometry H) stanovilo pro samostatný oblouk ve vrcholu průhyb w0 = 17,0 mm, zatímco pro oblouk s membránou byl tento průhyb po předpětí zcela eliminován.
2.3 Deformace oblouků pod zatížením
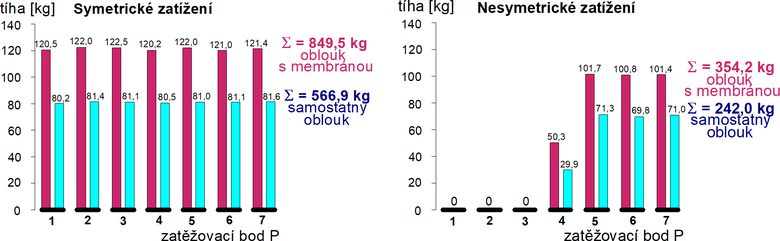
a) Symetrické zatížení
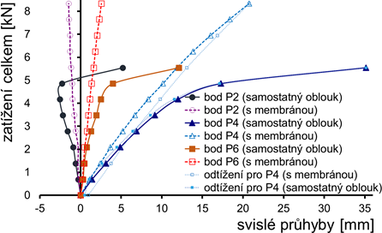
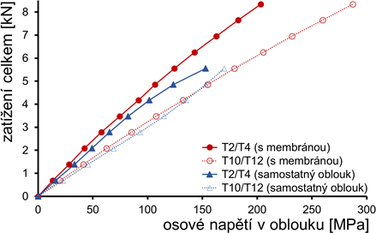
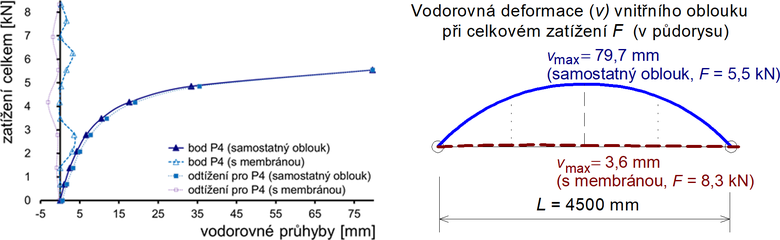
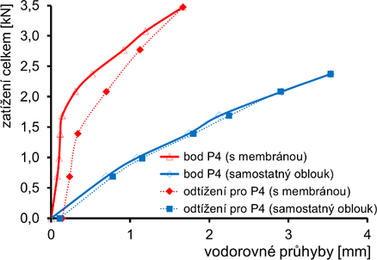
Svislé průhyby a napětí v patce vnitřního vyšetřovaného oblouku jsou uvedeny na obr. 5, vodorovné deformace na obr. 6. Vzhledem k pružnému a téměř lineárnímu chování oblouku jsou hodnoty průhybů pro odtížení uvedeny pouze pro finální maximální zatížení. Samostatný oblouk náhle prudce vybočil z roviny oblouku a zatěžování bylo ukončeno při celkovém zatížení zhruba F0 = 5,5 kN. Následný test s obloukem stabilizovaným membránou byl ukončen při zatížení FM = 8,3 kN (rozhodnuto pro zachování pružného chování oblouku), přitom svislé průhyby rostly téměř lineárně a vodorovné byly nepatrné. Očekávaná stabilizace oblouku membránou byla tedy mimořádná.
b) Nesymetrické zatížení
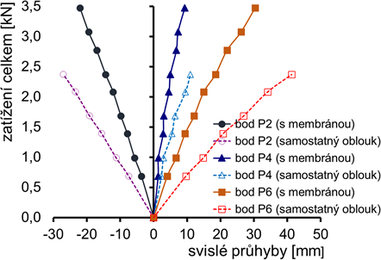
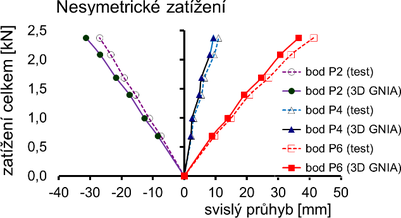
Zásadní stabilizaci oblouku membránou i při nesymetrickém zatížení ukazuje obr. 7. Zkouška samostatného oblouku byla ukončena při zatížení F0 = 2,37 kN pro nadměrné nesymetrické deformace v bodech P2 (resp. P6), se svislými průhyby δ0 = 41,3 (−27,0) mm a vodorovnými průhyby ν0 = 3,5 mm. Oblouk stabilizovaný membránami se pro stejné zatížení (FM = F0 = 2,37 kN) deformoval mnohem méně, se svislým průhybem δM = 18,5 (−14,4) mm a vodorovným průhybem ν0 = 0,5 mm. Stabilizační efekt pro svislé průhyby tak činí 55 % a pro vodorovné průhyby 86 %. Ukázalo se, že stabilizační efekt membrány na deformace i napjatost oblouku se výrazně projevuje jak u symetrických, tak i nesymetrických zatíženích.
3. Numerická analýza
Hlavním cílem je sestavení numerického modelu k úspěšné validaci na experimentech a k následné rozsáhlé parametrické studii oblouků podpírajících membránové konstrukce [28]. Použit byl software SOFiSTiK [21], který patří mezi přední softwary k řešení membránových konstrukcí. Vzhledem k subtilnosti podpůrné konstrukce a velkým deformacím v pružném stavu byla zvolena 3D GNIA (geometricky nelineární analýza s imperfekcemi) bez materiálové nelinearity (tj. pružnostní řešení), pro membrány navíc materiálový model Galliota a Luchsingera [15]. K numerickému řešení byla použita modifikovaná Newton-Raphsonova iterace (mN-R) s Crisfieldovou akcelerací (metoda arc-length). V průběhu řešení se pro volené přírůstky zatížení nebo předpětí použilo vždy 50 iterací, pro které byl splněn i požadavek defaultní přesnosti řešení.
3.1 Samostatný oblouk
Orientačně (i vzhledem k následující parametrické studii [28]) byla vyšetřena stabilita ideálního vnitřního oblouku, tj. kritické zatížení, pomocí lineární bifurkační analýzy (LBA). Oblouk je v podporách plně vetknutý (rozměr L/H = 4500×1200 [mm]). Pro svislé symetrické rovnoměrné zatížení po délce oblouku vycházejí kritická celková zatížení Ncr,sym,celkové,1 = 7,97 kN (z roviny s jednou půlvlnou) a Ncr,sym,celkové,2 = 9,19 kN (v rovině dvě půlvlny). Pro svislé nesymetrické rovnoměrné zatížení Ncr,nesym,celkové,1 = 7,91 kN (z roviny s jednou půlvlnou) a Ncr,nesym,celkové,2 = 9,08 kN (v rovině dvě půlvlny).
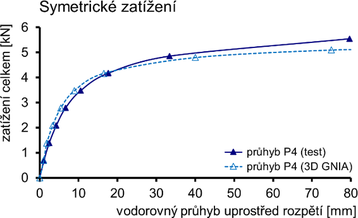
Laboratorní samostatný oblouk s počáteční vodorovnou deformací w0 = 17,0 mm byl vyšetřován 3D GNIA. Použity byly nelineární prvky BEAM s délkou 100 mm. Výsledky řešení a porovnání s testy jsou na obr. 8.
Pro symetrické zatížení z porovnání s kritickým břemenem (7,97 kN) plyne, že vliv imperfekce je podstatný, avšak numerická únosnost imperfektního oblouku (5,1 kN) je v dobré shodě s experimentem (5,5 kN). Pro nesymetrické zatížení je shoda výsledků testu a numerického řešení rovněž dobrá, avšak test byl ukončen z důvodu velkých průhybů subtilního oblouku předčasně pro jeho zachování k testům s membránou.
3.2 Oblouk stabilizovaný membránou
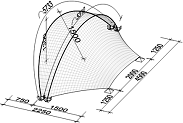
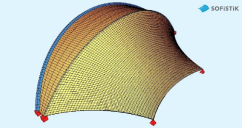
Obr. 9 Vytvoření geometrie (hranice modelu, vpravo membrána s nejmenší plochou)
Počáteční tvar oblouků a obvodových lanek byl před testem zaměřen. Pro vyšetřovaný vnitřní oblouk byl oproti ideálnímu tvaru zjištěn ve svislém směru mírně antisymetrický tvar (+10,0 mm v místě V1 a −10 mm v místě V3) a ve vodorovném směru ve vrcholu (v místě H2) průhyb 5,5 mm. V nadstavbovém programu pro AutoCAD – SOFiCAD byly odtud vytvořeny hraniční křivky (pro oblouky a obvodová lanka), automaticky generovány plochy s nejmenší plochou a exportovány do programu SOFiSTiK (obr. 9).
Membrány Précontraint FERRARI® 702S umožňuje program modelovat podle výzkumu Galliota a Luchsingera [15]. Ortotropní charakteristiky byly zavedeny pěti parametry následovně: pro poměr napětí ve směru osnovy (kolmo na oblouk) a útku 1:1 jsou moduly pružnosti Ew1:1 = 634.9 kN/m a Ef1:1 = 661.9 kN/m, změny modulů pro jiné poměry napětí jsou ΔEw = 295 kN/m and ΔEf = 168 kN/m a Poissonova konstanta ν = 0,196. Uvedené jednotky napětí i modulů se běžně u membrán používají, neboť tloušťka membrány není jednoznačně definována. Pro vstupní data programu byly hodnoty transformovány pro reálnou tloušťku 0,7 mm (odtud Ew1:1 = 907.0 MPa, Ef1:1 = 945.6 MPa).
Uložení membrán na obloucích je v celé délce modelováno jako kloubové (tzv. pianový kloub), zatímco při experimentu je na vnitřním oblouku realizováno vystřídanými „kapsami“. Membrány byly pokryty sítí čtyřúhelníkových nelineárních prvků (MEMBRANE) se zjemněním v rozích. Pro zjištění citlivosti na membránovou napjatost pod zatížením byly zadány sítě s nejdelší hranou 25, 50, 100 a 200 [mm]. Výsledky pro krajní dělení se lišily méně než o 0,2 %, zatímco výpočetní čas vzrostl 107krát. Pro další výpočty byla proto použita síť s dělením 50 mm.
Předpětí membrán ve 3D GNIA bylo přímo zavedeno v lokálních osách konečných prvků. V obvodových lankách bylo příslušné předpětí odvozeno ze vztahu:
kde je
- S
- předpětí v obvodovém lanku [kN],
- r
- poloměr zakřivení lanka [m],
- P
- předpětí v membráně kolmo na lanko [kN/m].
Zavedení předpětí v membráně a obvodových lankách bylo provedeno v 10 přírůstcích a generovalo výchozí rovnovážný tvar nezatížené membrány (oproti tvaru s nejmenší plochou na obr. 9 mírně „prohnutější“).
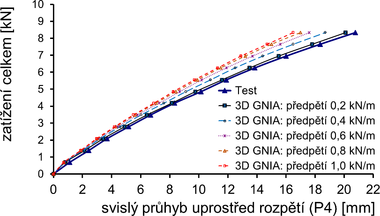
Následně bylo aplikováno rovnoměrné svislé zatížení na vnitřní oblouk v 10 přírůstcích jako při experimentu. Závislost svislého průhybu vnitřního (zkoumaného) oblouku na velikosti předpětí při symetrickém zatížení ukazuje obr. 10.
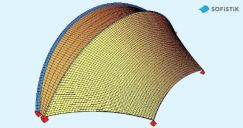
Obr. 10 Model konstrukce po zavedení předpětí a svislý průhyb středního oblouku při symetrickém zatížení a různém předpětí
Předpětí membrány při testu podle orientačních měření na povrchu membrán (viz odst. 2.1) bylo mezi 0,10 (kolmo na oblouky) až 0,31 kN/m (ve směru oblouků). Nejistota kromě vlivu měření na povrchu membrán místo v jejich vnitřní struktuře spočívá dále v přípoji navlečených membrán na oblouk prostřednictvím „kapes“ oproti kontinuálnímu spojení v numerické analýze. Nicméně numerické řešení s předpětím 0,2 kN/m, které lze považovat za blízké hodnotě při testech, velmi dobře koresponduje s výsledky měření.
4. Závěr
V laboratoři Fakulty stavební ČVUT byl testován štíhlý ocelový oblouk a poté jeho stabilizace textilní membránou. V první fázi byl symetricky a nesymetricky liniově zatěžován vetknutý oblouk s průměrem trubky ø 26,9×3,2 [mm], rozpětím 4500 mm a vzepětím 1200 mm. Byly zaměřeny počáteční deformace, osazeny měřicí přístroje a zaznamenáno prostorové chování oblouku pod zatížením.
Poté byl přidán další vnější oblouk, obvodová lanka a pokrytím membránou z polyesterové tkaniny (Précontraint FERRARI® 702S) byl vytvořen model přístřešku. Chování původního vnitřního oblouku po předpětí membrán a obvodových lanek bylo monitorováno jako u samostatného oblouku. Porovnáním výsledků byl stanoven vliv stabilizace membránou na stabilitní prostorové chování vnitřního oblouku.
Numerický model samostatného oblouku i membránové konstrukce byl sestaven v programu SOFiSTiK. Použita byla pružnostní geometricky nelineární analýza s počátečními imperfekcemi (GNIA). Popsána jsou vstupní data, ortotropní model membrán, sítě prvků, zavedení předpětí membrán i okrajových lanek.
Výsledky numerického řešení byly porovnány s výsledky testů s velmi dobrou shodou. Validace numerického modelu byla cílem této první části článku. Použité numerické řešení je proto použito v druhé části článku pro rozsáhlé studie stability oblouků podpírajících membránové válcové konstrukce (viz [28]).
5. Literatura
- Serge Ferrari: https://www.sergeferrari.com/serge-ferrari/our-technologies. (Přístup 2021).
- Sattler PRO-TEX: Fabrics engineered to perfection. https://protex.sattler.com/en/home. (Přístup 2021).
- Architen Landrell: https://www.architen.com/materials/tenara/. (Přístup 2021).
- Cabot: https://www.cabotcorp.com/solutions/applications/construction/tensile-roofing. (Přístup 2021).
- Seidel, M.: Tensile surface structures - A practical guide to cable and membrane construction. John Wiley & Sons, 2009, 240 s.
- Jermoljev, D.: Implementace nekovových membrán do ocelových konstrukcí. Ph.D. disertace, FSv ČVUT, 2014, 113 s.
- Svoboda, O.: Stabilizace ocelového oblouku nekovovou membránou. Ph.D. disertace, FSv ČVUT, 2019, 149 s.
- Lewis, W. J.: Tension Structures – Form and Behaviour, Thomas Telford Publishing, 2003, 201 s.
- Čápová, J.: Modelování membránových konstrukcí. Ph.D. disertace, FSv ČVUT, 2010, 132 p.
https://mat.fsv.cvut.cz/doktorandi/files/JC.pdf. (Přístup 2021). - Foster, B. a Mollaert, M.: European Design Guide for Tensile Surface Structures, TensiNet, 2004, 354 s.
- Wakefield, D. S.: Engineering analysis of tension structures: Theory and practice. Eng. Structures, sv. 21, č. 8, 1999, s. 680-690. https://www.sciencedirect.com/science/article/abs/pii/S0141029698000236?via%3Dihub. (Přístup 2021).
- Kato, S., Yoshino, T. a Minami, H.: Formulation of constitutive equations for fabric membranes based on concept of fabric lattice model. Eng. Structures, sv. 21, č. 8, 1999, s. 691-708. https://www.sciencedirect.com/science/article/abs/pii/S0141029698000248?via%3Dihub. (Přístup 2021).
- Dinh, T. D., Rezaei, A., De Laet, L., Mollaert, M., Van Hemelrijck, D. a Van Paepegem W. A: A new elasto-plastic material model for coated fabric. Eng. Structures, sv. 71, 2014, s. 222-233. https://www.sciencedirect.com/science/article/abs/pii/S0141029614002405?via%3Dihub. (Přístup 2021).
- Pargana, J. B. a Leitao, W. M. A: A simplified stress-strain model for coated plain-weave fabrics used in tensioned fabric structures, Eng. Structures, sv. 84, 2015, s. 439-450.
https://www.sciencedirect.com/science/article/abs/pii/S0141029614007433. (Přístup 2021). - Galliot, C. a Luchsinger, R. H.: A simple model describing the non-linear biaxial tensile behaviour of PVC/coated polyester fabrics for use in finite element analysis, Composite Structures, sv. 90, č. 4, 2009, s. 438-447.
https://www.sciencedirect.com/science/article/abs/pii/S0263822309001172?via%3Dihub. - SOFiSTiK 2014. https://www.sofistik.de/. (Přístup 2021).
- Gosling, P.: Basic Philosophy and calling notice, Tensinet analysis & Material working group, Tensinews 13, 2007
- Machacek, J. a Jermoljev, D.: Steel structures in interaction with non-metallic membranes, J. Civil Engineering & Management, sv. 23, č. 3, 2017, s. 368-377. https://journals.vgtu.lt/index.php/JCEM/article/view/973. (Přístup 2021).
- Technet gmbh Berlin-Stuttgart, Easy. https://www.technet-gmbh.com/en/products/easy/. (Přístup 2021).
- ixCube 4-10. http://www.ixray-ltd.com/index.php?option=com_content&view=featured&Itemid=435. (Přístup 2021).
- SOFiSTiK 2014. https://www.sofistik.de/. (Přístup 2021).
- membrane NDN software. https://www.ndnsoftware.com/. (Přístup 2021).
- Dlubal software pro navrhování a analýzu membránových a textilních konstrukcí.
https://www.dlubal.com/cs/reseni/odvetvi/membranove-konstrukce. (Přístup 2021). - Gale, S. a Lewis, W. J.: Patterning of tensile fabric structures with a discrete element model using dynamic relaxation. Computers & Structures, sv. 169, 2016, s. 112-121. https://www.sciencedirect.com/science/article/pii/S0045794916300608?via%3Dihub. (Přístup 2021).
- Archtex: http://www.archtex.cz/cs/index-onas.html. (Přístup 2021).
- Jermoljev D.: Ocelové konstrukce a membrány. Excon.
https://ocelvarchitekture.cz/prednasky/Ocelvarch_Excon_Jermoljev_Ocelove_konstrukce_a_membrany.pdf. (Přístup 2021). - Janata, V., Jermoljev D. a Koupený, P.: Baldachýn pro Svatého Otce v Brně Tuřanech. Konstrukce č. 5, 2009, s. 28–29.
- Macháček, J. a Svoboda, O.: Ocelové oblouky stabilizované membránami. Část 2: Parametrické studie ocelových oblouků stabilizovaných membránami. TZB-info, ocelové konstrukce, podáno k tisku.
- Warner Shelter Systems Limited - Dome Stagecover, Calgary. https://www.wssl.com/sc_prod.html. (Přístup 2021).
- Laboratorium BLUM Stuttgart, Report on biaxial tests Précontraint 702, 2005, 8 s.
Poděkování
Článek a související výzkum vznikl za podpory grantu SGS19/150/OHK1/3T/11. Poděkování patří centrálním laboratořím Fakulty stavební ČVUT a firmě Archtex s.r.o. Praha za asistenci při experimentech.
Článek se zabývá velmi aktuálním a současně zajímavým a atraktivním tématem z oblasti stavebního inženýrství, které však v ČR není předmětem nijak masového zájmu výzkumníků. Experimentální analýza zahrnující zkoušky laboratorního modelu reálného tvaru a uspořádání v měřítku cca 1:10 je vhodným a účelným prostředkem pro získání informací o skutečném působení konstrukce zejména z hlediska stability oblouku, již může příznivě ovlivnit stabilizační efekt membrány, který se výrazně projevuje jak u symetrických, tak i nesymetrických zatížení. Výsledky zatěžovacích zkoušek laboratorního modelu poskytly vstupy pro verifikaci a validaci numerického modelu, který byl pro testovanou konstrukci vytvořen pomocí softwaru SOFiSTiK. Vytvořený numerický model, který byl ověřen a porovnán s výsledky testů, se ukazuje jako vhodně použitelný pro numerické modelování chování konstrukcí uvedeného typu a umožní numerické simulace pro účely zamýšlených rozsáhlejších studií stability oblouků podpírajících membránové válcové konstrukce. Předložený článek poskytuje jednak teoretické výsledky získané z numerického modelu a popisující chování konstrukce daného typu, jednak informace o skutečném chování konstrukce zjištěné experimentálně a prakticky využitelné pro další zkoumání v této oblasti. Předložený článek doporučuji k publikaci.
The article describes and analyses testing of a shelter model with a textile membrane supported by a steel tube arch. The goal of the investigation is the spatial behaviour of the arch regarding its design. The difference in behaviour of the build-in arch alone and the one in the membrane structure is investigated. The entry data, prestressing and loading procedures are shown including test results. SOFiSTiK software was used for the elastic geometrically nonlinear analysis with imperfections (GNIA) respecting the orthotropic behaviour of the membrane (Précontraint FERRARI®). The successful validation of numerical results by tests warrants the extensive parametrical studies dealing with stability of arches in barrel type membrane structures in the second Part of the article.