Příklady výpočtu podle Eurokódu 5 (IV.)
První tři části seriálu sloužily k seznámení s vývojem norem a jako podklady pro samotné výpočty podle Eurokódu 5 (ČSN EN 1995-1-1) a ČSN 73 1702 (modifikovaná DIN 1052:2004). Předmětem částí 4 a 5 jsou praktické příklady výpočtu. Vzhledem k tomu, že tyto postupy nejsou u nás příliš zažité, považujeme za velmi prospěšné se tomuto tématu dále věnovat.
Příklady 1 až 8
Předmluva a pomocné podklady pro výpočet viz část 1 až část 3.
POZNÁMKA Tyto příklady univerzity Wismar jsou určeny pro výroční a závěrečné zkoušky studentů. Příklady jsou zpravidla zaměřeny na určité dílčí posouzení nosného prvku nebo konstrukce (například vzpěrné pevnosti, nebo únosnosti v ohybu, nebo pevnosti spojovacích prostředků, deformace apod.) v souladu se zadáním. Nejde tedy o komplexní posouzení, které se požaduje v praxi. Na tento aspekt upozorňujeme v některých příkladech v poznámce.
V uvedených příkladech jsou na rozdíl od originální německé verze zavedeny aktuální hodnoty návrhové pevnosti homogenního lepeného lamelového dřeva podle tabulky 4. Ty jsou stanoveny na základě charakteristických hodnot podle ČSN EN 14080, tabulka 5, se součinitelem γM = 1,25 (ČSN EN 1995-1-1, tabulka 2.3). Originální verze vychází z v Německu dosud platných charakteristických hodnot podle dřívější ČSN EN 1194, tabulka 1, a součinitele γM = 1,3. Při výpočtech v praxi je třeba použít aktuální platné hodnoty.
Příklad 1
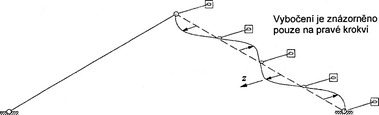
Má se ověřit, zda znázorněná střecha s posuvným hambálkem má dostatečnou bezpečnost proti vybočení. Dvojitá krokev má vždy dvojitý průřez ze dvou částí, které nejsou vzájemně spojeny.
Návrhová hodnota tlakové síly v dvojité krokvi je Fd = 115 kN
Podmínky použití: třída trvání zatížení krátkodobé a třída provozu 1.
Má se stanovit vzpěrná délka a posoudit stabilita
- a) pro vzpěr k ose y (vybočení ve směru z) při uvážení, že všechny dvojité krokve jsou ve směru z udržovány ve stejných vzdálenostech, jak je znázorněno na pravé krokvi
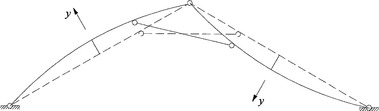
- b) pro vzpěr k ose z (vybočení ve směru y)
POZNÁMKA V tomto příkladu je posuzována krokev výlučně na vzpěr. V hambalkovém krovu je krokev obecně namáhána také na ohyb a je třeba posoudit také namáhání ohybem včetně průhybu. Významné je také posouzení vodorovné reakce v podpoře hambálkové soustavy.
Řešení příkladu 1
a) Vzpěr k ose y (vybočení ve směru z, tedy kolmo k rovině nákresu)
b) Vzpěr k ose z (vybočení ve směru y, tedy v rovině nákresu)
Příklad 2
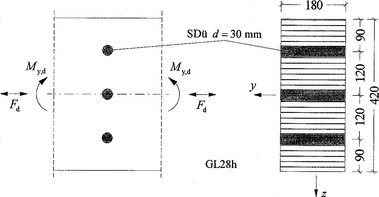
Nosník z lepeného lamelového dřeva GL28h je namáhaný v jedné kombinaci zatížení jednoosým ohybem a tahem a v druhé kombinaci zatížení jednoosým ohybem a tlakem. Nosník je zabezpečen proti klopení.
Má se posoudit únosnost v těchto krocích:
- a) ověřit, zda může být vypočten průřezový modul netto Wy,n vztažený k těžišťové ose neoslabeného průřezu (vrtaný otvor pro kolík (SDü) uprostřed lze přitom zanedbat)
- b) výpočet průřezového modulu netto Wy,n (vrtaný otvor uprostřed lze přitom zanedbat)
- c) výpočet plochy průřezu netto An a posouzení únosnosti pro kombinaci zatížení My,d = 62,3 kNm a Fd = 214 kN (tah)
- d) výpočet plochy průřezu netto An a posouzení únosnosti pro kombinaci zatížení My,d = 62,3 kNm a Fd = 270 kN (tlak)
Podmínky použití: třída trvání zatížení střednědobé a třída provozu 1.
Řešení příkladu 2
kh,y = 1,036
fm,d = 1,036 ‧ 17,9 = 18,5 N/mm2
ft,0,d = 1,036 ‧ 14,3 = 14,8 N/mm2 návrhové pevnosti viz odst. 2.1, tabulka 4
a) Ověření, zda může být vypočten modul průřezu netto Wy,n vztažený k těžišťové ose neoslabeného průřezu
b) Výpočet průřezového modulu Wy,n netto
c) Posouzení únosnosti pro tah a ohyb viz ČSN EN 1995-1-1, 6.2.3
d) Posouzení únosnosti pro tlak a ohyb viz ČSN EN 1995-1-1, 6.2.4
Příklad 3
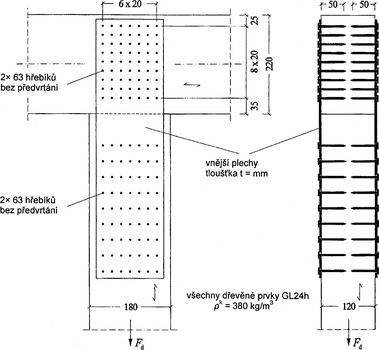
Na horizontální nosník je zavěšen svislý prut pomocí dvou vnějších ocelových plechů a profilovaných hřebíků třídy únosnosti 3
- a) Má se zkontrolovat uspořádání hřebíků ve dřevě pouze v horní skupině.
- b) Pro jeden hřebík se má stanovit návrhová hodnota maximální únosnosti Fax,Rd pro namáhání ve směru osy hřebíku (vytažení). Porušení protažením hlavy není rozhodující.
- c) Pro jeden hřebík se má stanovit návrhová hodnota maximální únosnosti Fv,Rd (střih) pro namáhání kolmo k ose hřebíku (Johansenův podíl pro smyk). Vnější plechy se uvažují jako tlusté.
- d) Pro jeden hřebík se má stanovit návrhová hodnota maximální únosnosti Fv,Rd při uvážení únosnosti na vytažení. Z této únosnosti hřebíků se má stanovit pro horní skupinu maximální návrhová síla Fd.
- e) Má se stanovit maximální návrhová tahová síla Fd z posouzení únosnosti namáhání v tahu pro dolní dřevěný prvek při uvážení zvláštních pravidel pro spoje namáhané tahem.
Všechny hřebíky jsou profilované hřebíky třídy únosnosti 3, d = 4,6 mm, nepředvrtané.
Třída trvání zatížení střednědobé a třída provozu 1 (kmod = 0,80)
Řešení příkladu 3:
a) Kontrola uspořádání hřebíků v horním dřevěném prvku viz ČSN EN 1995-1-1, tabulka 8.2
| α = 90°; d = 4,6 mm | min vzdálenost | existující | |
|---|---|---|---|
| a1 | 0,7 ‧ (5 + 5 ‧ cos α) ‧ d → 3,5 ‧ d | 16,1 mm | 20 mm |
| a2 | 0,7 ‧ 5 ‧ d → 3,5 ‧ d | 16,1 mm | 20 mm |
| a3,t | − − − | − − − | − − − |
| a3,c | − − − | − − − | − − − |
| a4,t | (5 + 2 ‧ sin α) ‧ d → 7 ‧ d | 32,2 mm | 35 mm |
| a4,c | 5 ‧ d | 23 mm | 25 mm |
b) Stanovení návrhové hodnoty Fax,Rd (vytažení)
c) Stanovení návrhové hodnoty Fv,Rd,Joh (Johansenův podíl smyku) viz odst. 2.5.2, tabulka 10
d) Maximální návrhová síla Fv,Rd z únosnosti hřebíků nahoře
Pro profilové hřebíky je součinitel kJoh = 0,50
Posouzení únosnosti pro jednu střihovou plochu jednoho spojovacího prostředku v podélném směru
kde je
- Fd
- návrhová hodnota střihového namáhání,
- Fv,Ed
- návrhová hodnota střihového namáhání na střihovou spáru jednoho spojovacího prostředku,
- n
- počet spojovacích prostředků v jedné řadě za sebou ve směru vláken,
- m
- počet řad spojovacích prostředků kolmo ke směru vláken,
- p
- počet střihových spár na jeden spojovací prostředek,
- n ‧ m ‧ p
- celkový počet střihových spár pro přenos síly Fd
e) Maximální návrhová síla Fv,Rd z únosnosti dolního dřevěného prvku
Příklad 4
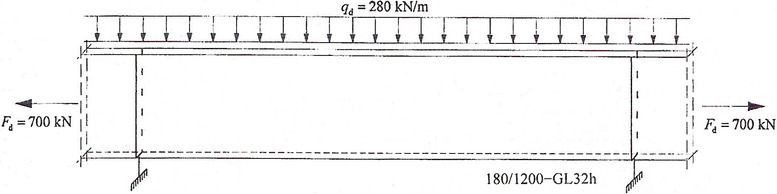
Na následujícím obrázku je znázorněno střední pole spojitého nosníku. Nosník je zatížen rovnoměrným zatížením a tahovou silou Fd.
Maximální moment je Md = 786,9 kNm.
Má se posoudit stabilita proti klopení pro třídu trvání zatížení krátkodobé a třídu provozu 1.
Řešení příkladu 4
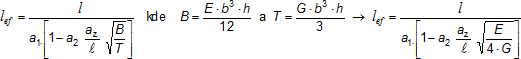
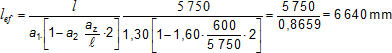
Jednoosý ohyb a tah:
Příklad 5
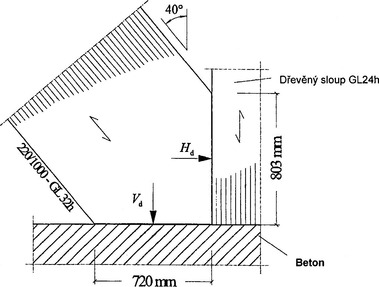
Příhradový prut z lepeného lamelového dřeva odkloněný od svislého směru o 40° je uložen v průsečíku horizontální betonové desky a svislého sloupu z lepeného lamelového dřeva.
Má se vypočítat maximální únosnost dále znázorněného podporového styčníku v těchto krocích:
- a) maximální návrhová hodnota horizontální podporové reakce Hd
- b) maximální návrhová hodnota vertikální podporové reakce Vd
Podmínky použití: třída trvání zatížení střednědobé a třída provozu 1.
Řešení příkladu 5
Viz ČSN EN 1995-1-1, 6.1.4 a 6.1.5, ČSN 73 1702, 10.2.4.
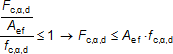
a) maximální návrhová hodnota horizontální reakce Hd
− z posouzení napětí v tlaku příhradového prutu GL32h
− z posouzení napětí v tlaku na svislém dřevěném sloupu GL24h
b) maximální návrhová hodnota vertikální podporové reakce Vd
pro fc,0,d = 20,5 a fc,90,d = 1,6 N/mm2
Příklad 6
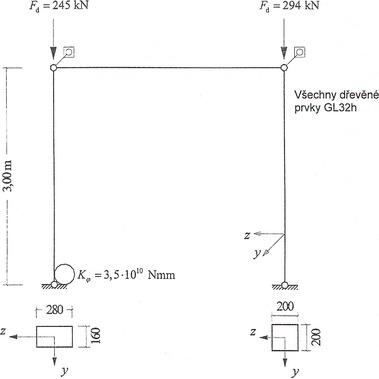
Pro soustavu na obrázku se má ověřit, zda při daném zatížení vykazuje dostatečnou bezpečnost proti vybočení. Stanovte vzpěrné délky a ověřte stabilitu.
- a) pro vybočení soustavy vybočením levé stojky k ose y (vybočení ve směru z)
- b) pro vybočení pravé stojky
Podmínky použití: třída trvání zatížení krátkodobé a třída provozu 1.
Řešení příkladu 6
a) Vybočení systému vybočením levé stojky k ose y
b) Vybočení pravé stojky
Příklad 7
Na jednodílný horizontální nosník se má připojit jednodílný šikmý tažený prut pomocí vnitřního ocelového plechu a kolíků (SD) /přesných svorníků (PB).
Návrhová hodnota tahové síly je Fd = 160 kN
Má se posoudit únosnost v těchto krocích:
- a) ověřit uspořádání kolíků (SD) / přesných svorníků (PB) v šikmém taženém prutu
- b) ověřit uspořádání kolíků v horizontálním nosníku
- c) posoudit únosnost spojovacích prostředků v šikmém taženém prutu. Únosnost přesných svorníků (PB) v tahu se neuvažuje
- d) posoudit únosnost spojovacích prostředků v horizontálním nosníku.
Podmínky použití: třída trvání zatížení krátkodobé a třída provozu 1 (kmod = 0,90)
POZNÁMKA Posouzení blokovým smykem podle ČSN EN 1995-1-1, Příloha A, Změna A2, zde není uvažováno.
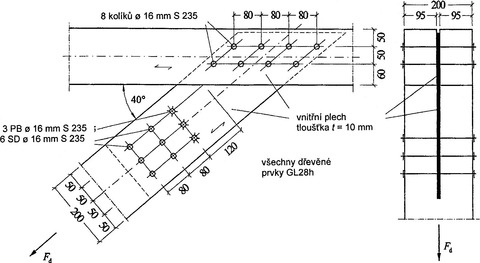
Řešení příkladu 7
a) Ověření uspořádání kolíků (SD) / přesných svorníků (PB) v šikmém taženém prutu
| Předpis při α = 0° | nejméně [mm] při d = 16 mm | použito [mm] | |
|---|---|---|---|
| a1 | (3 + 2 ‧ cos α) ‧ d = 5 ‧ d | 80 | 80 |
| a2 | 3 ‧ d | 48 | 50 |
| a3,t | max {7 ‧ d ; 80 mm} | 112 | 120 |
| a3,c | − − − | − − − | − − − |
| a4,t | − − − | − − − | − − − |
| a4,c | 3 ‧ d | 48 | 50 |
viz ČSN EN 1995-1-1, tabulka 8.5
b) Ověření uspořádání kolíků (SD) / přesných svorníků (PB) v horizontálním nosníku
| Předpis při α = 0° | nejméně [mm] při d = 16 mm | použito [mm] | |
|---|---|---|---|
| a1 | (3 + 2 ‧ cos α) ‧ d = 4,53 ‧ d | 72,5 | 80 |
| a2 | 3 ‧ d | 48 | 50 |
| a3,t | − − − | − − − | − − − |
| a3,c | − − − | − − − | − − − |
| a4,t | max {(2 + 2 ‧ sin α) ‧ d ; 3 ‧ d } | 52,6 | 60 |
| a4,c | 3 ‧ d | 48 | 50 |
c) Posouzení únosnosti spojovacích prostředků v šikmém taženém prutu viz odst. 2.5.4, tabulka 13
Posouzení únosnosti pro jednu střihovou plochu jednoho spojovacího prostředku v podélném směru
kde je
- Fd
- návrhová hodnota střihového namáhání,
- Fv,Ed
- návrhová hodnota střihového namáhání na střihovou spáru jednoho spojovacího prostředku,
- n
- počet spojovacích prostředků v jedné řadě za sebou ve směru vláken,
- m
- počet řad spojovacích prostředků kolmo ke směru vláken,
- p
- počet střihových spár na jeden spojovací prostředek,
- n ‧ m ‧ p
- celkový počet střihových spár pro přenos síly Fd
Únosnost spoje s více spojovacími prostředky za sebou ve směru vláken může být u dřevěných prvků vzhledem k riziku štípání výrazně menší. Než součet únosností jednotlivých spojovacích prostředků. Pro každý připojovaný dřevěný prvek musí být splněna podmínka
kde je
- Fv,Ed ‧ cos α
- podíl střihového namáhání jednoho spojovacího prostředku na střihovou spáru ve směru vláken,
- Fv,Rd
- návrhová hodnota únosnosti jednoho spojovacího prostředku ve směru vláken,
- α
- úhel mezi střihovou silou a směrem vláken 0° ≤ α ≤ 90°,
- n
- počet spojovacích prostředků za sebou ve směru vláken v jedné řadě,
- nef
- účinný počet spojovacích prostředků za sebou v jedné řadě viz část 1, tabulka 5
Po dosazení
d) Posouzení únosnosti spojovacích prostředků v horizontálním nosníku
Posouzení únosnosti pro jednu střihovou plochu jednoho spojovacího prostředku ve směru zatížení
Posouzení únosnosti pro jednu střihovou plochu jednoho spojovacího prostředku pro komponenty sil ve směru vláken
Příklad 8
- a) Proveďte posouzení tahových napětí pro dřevo šikmého taženého prutu z příkladu 7 pro třídu trvání zatížení krátkodobé a třídu provozu 1 při uvážení zvláštních pravidel pro tažené spoje.
- b) Tři přesné svorníky ve skloněném taženém prutu z příkladu 7 jsou navíc zatíženy na vytažení. Vypočtěte návrhovou hodnotu tahové síly Ft,d, kterou musí tyto tři přesné svorníky společně přenést.
Řešení příkladu 8
a) Posouzení únosnosti šikmého taženého prutu při uvážení zvláštních pravidel pro tažené spoje
b) Tahová síla ve svornících namáhaných na vytažení
Calculation according to Eurocode 5 examples 1 to 8. Preface and helping data for calculation see Part 1 to 3.
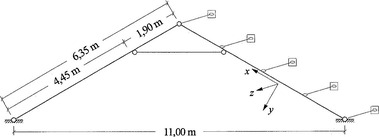
![Krokev C24 [mm]](/docu/clanky/0139/013913o4.jpg)