Skutočný pracovný diagram ocele a jeho použitie v konečnoprvkových simuláciach
Počítačové simulácie vyžadujú vhodné vstupné parametre, aby došlo k zhode výsledkov numerických simulácii a experimentov. Skutočný pracovný diagram, vhodný pre numerické simulácie, popisuje nelineárne správanie sa ocele od počiatku zaťažovania až po porušenie vzorky. Časť po pevnosť v ťahu je možné jednoducho popísať analytickými metódami, no oblasť lokálnej plastickej deformácie nie je možné popísať podobnými závislosťami medzi technickým a skutočným diagramom. Bola vykonaná numerická ťahová skúška skúšobnej vzorky pre stanovenie skutočného diagramu ocele v programe ANSYS. Napätia a deformácie z počítačových simulácií boli porovnané s výsledkami experimentálnej ťahovej skúšky.
1. Úvod
S rastúcou náročnosťou simulácií v stavebníctve rastie aj požiadavka na vhodné vstupné parametre výpočtov. Konkrétne v prípade oceľových konštrukcií je niekedy nedostatočné riešiť problémy len v lineárno-elastickej oblasit, ale je potrebné analyzovať aj plastické správanie sa prvkov, a to je často problém správne zohľadniť. V bežnej inžinierskej praxi často postačuje použiť ako materiálovú charakteristiku bilineárny pracovný diagram ocele, no za účelom porovnania výsledkov experimentov so simuláciami je vhodné použiť technický pracovný diagram ocele, ľahko získaný a prepočítaný z výsledkov ťahovej skúšky.
V konečnoprvkových softvéroch (napr. ANSYS) je vhodné ako materiálový parameter použiť skutočný pracovný diagram ocele. Získať ho možno konverziou z technického pracovného diagramu pomocou logaritmických rovníc. Táto metóda sa dá použiť len na časť pracovného diagramu, kde sú pomerné pretvorenia konštantné na meranej dĺžke (od počiatku zaťažovania po pevnosť v ťahu). Problémom môže byť zvyšná časť diagramu, kedy dochádza k vytváraniu zúženia prierezu, tzv. krčka. Vzhľadom na vyššie uvedené predpoklady sa logaritmické rovnice v tejto oblasti využiť nedajú a je potrebné zvoliť inú metódu, napríklad iteratívnu metódu založenú na postupnom určovaní skutočného pracovného diagramu v oblasti vytvárania krčka.
2. Teoretické východiská
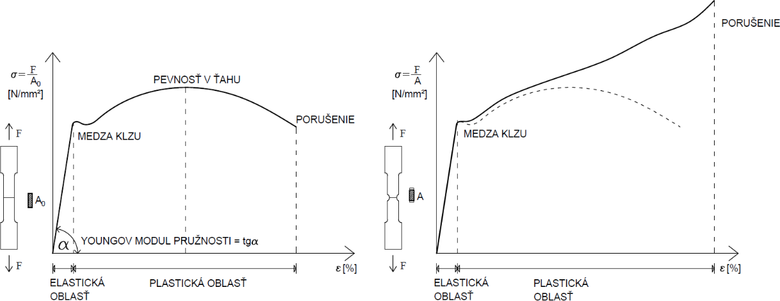
Vo všeobecnosti je možné tvrdiť, že výsledkom ťahovej skúšky je krivka (pracovný diagram) vyjadrujúca vzťah medzi napätím a predĺžením, podobná technickému pracovnému diagramu ocele. Na to, aby sa z výsledku ťahovej skúšky stal technický pracovný diagram ocele, je potrebné predĺženie prerátať na pomerné pretvorenie pomocou meranej dĺžky závislej od typu vzorky a prierezovej plochy. Technický pracovný diagram ocele je vztiahnutý na neporušený počiatočný prierez skúšobnej vzorky a to je hlavný dôvod, prečo technický pracovný diagram ocele nie je možné použiť v konečnoprvkových simuláciách.
Z dôvodu, že pri numerickej simulácii sa tvar vzorky namáhaním deformuje, je potrebné konvertovať technický pracovný diagram ocele na skutočný, kde je deformácia vzorky v korelácii s predchádzajúcimi deformáciami. V prípade použitia technického pracovného diagramu v simuláciách je možné sa dopustiť značnej chyby vo výpočte, ktorá sa prejaví v celej plastickej oblasti diagramu.
Pomocou logaritmických rovníc je možné konvertovať technický diagram na skutočný a možno ich použitť na rozsiahlej oblasti diagramu – od začiatku zaťažovania po pevnosť v ťahu. Na zvyšnú časť diagramu je nutné použiť inú metódu z dôvodu vzniku krčku na skúšobnej vzorke. Skutočné pretvorenie je charakterizované podielom prírastku pretvorenia a aktuálnej dĺžky (1) a skutočné napätie sa dá vypočítať ako podiel osovej sily a aktuálnej plochy prierezu skúšobnej vzorky (2) [1]:
kde σe a εe sú napätia a pomerné pretvorenia vziahnuté pre technický diagram ocele, σt a εt sú napätia a pomerné pretvorenia vztiahnuté pre skutočný diagram ocele, L0 je pôvodná dĺžka a L je okamžitá dĺžka.
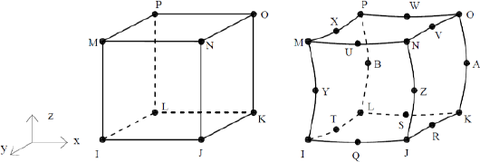
Jednou z možností na určenie druhej časti skutočného pracovného driagramu ocele je použitie iteratívnej metódy v konečnoprvkovom softvéri (napr. ANSYS), kde je skúšobná vzorka namodelovaná. Cieľom metódy je postupne určovať a upravovať priebeh skutočného diagramu v časti, kde sa tvorí krčok až po porušenie vzorky.
Procedúra spočíva v nasledovných krokoch: zvýšenie zaťaženia zavedením väčšieho premiestnenia, ako mal posledný počítaný bod; upravenie sklonu skutočného diagramu ocele (materiálová charakteristika ocele v numerickom modeli) tak, aby boli dosiahnuté dostatočne presné hodnoty napätia v technickom diagrame pri príslušnom pomernom pretvorení, t.j. sleduje sa hodnota reakcie v mieste, kde je v modeli zabránené deformácii vzorky v osi deformácie a predĺženie na meranej dĺžke, ktoré po prepočítaní na napätie a pomerné pretvorenie vytvoria technický diagram ocele. Tieto kroky sa opakujú, kým technický diagram získaný ako výsledok numerickej simulácie s technickým diagramom z ťahovej skúšky nie sú totožné až do porušenia vzorky. Výsledkom je skutočný diagram ocele (materiálová charakteristika ocele v numerickom modeli), ktorý možno použiť ako aj v iných konečnoprvkových simuláciách [1].
3. Model a ovplyvňujúce parametre
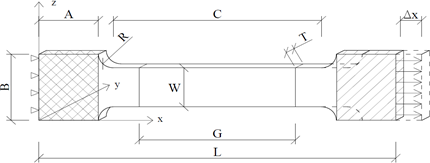
Obr. 2: Geometria skúšobnej vzorky
| A | B | C | L | G | W | R | T | |
|---|---|---|---|---|---|---|---|---|
| [mm] | 50 | 61 | 175 | 300 | 131,3 | 36 | 12,5 | 15 |
Pre účely vytvorenia skutočného diagramu ocele bola riešená vzorka ocele X60 (podľa API 5L) obdĺžnikového prierezu, s geometriou uvedenou na obrázku 2 a v tabuľke 1. Vo vyšrafovaných oblastiach modelu bola zabránená deformácia v smere osi z a v ľavej vyšrafovanej oblasti taktiež v smere osi x. Zaťaženie vo forme deformácie bolo aplikované v pravej šrafovanej oblasti.
V skúšobnom zariadení bola vzorka podrobená ťahovej skúške, výsledkom ktorej bola krivka závislosti napätia a predĺženia (obr. 3 vľavo), ktorá sa pomocou meranej dĺžky [2] prepočítala na pomerné pretvorenie. Malé nepresnosti boli vyhľadené a výsledkom bol technický pracovný diagram ocele (obr. 3 vpravo).
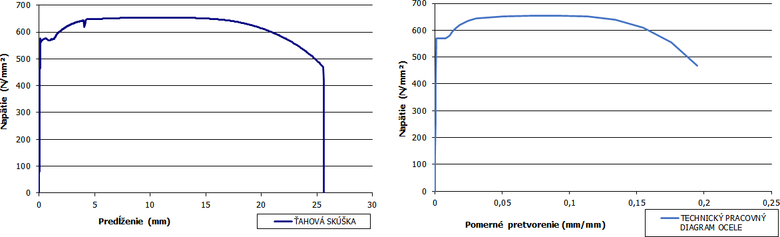
Obr. 3: Výsledok ťahovej skúšky (vľavo); technický pracovný diagram prepočítaný z výsledkov ťahovej skúšky a po vyhladení (vpravo)
Jedným z cieľov práce bolo zhodnotiť, aký vplyv na tvar skutočného diagramu majú veľkosť a typ (lineárny alebo kvadratický) konečných prvkov. Malé prvky vedia zvýšiť presnosť výsledku, no majú negatívny vplyv na výpočtový čas. Lineárne prvky sa vyznačujú vhodným pomerom presnosti a výpočtového času, kým kvadratické prvky zvyšujú výpočtový čas a pri porovnateľnej vzdialenosti uzlov konečných prvkov je výsledok menej presný.
Skúšobná vzorka bola namodelovaná v programe ANSYS v súlade s uvedenou geometriou. Celkovo boli vytvorené štyri modely – tri s lineárnymi elementami, každý s inou veľkosťou konečných prvkov (1 mm; 1,5 mm; 2 mm) a jeden s kvadratickými elementami veľkosti 1,5 mm.
Kvôli dosiahnutiu nielen pevnosti v ťahu, ale aj porušenia, a taktiež z dôvodu, že Newton-Raphsonov algoritmus neakceptuje klesajúcu vetvu pracovného diagramu, bolo potrebné vzorku zaťažovať prírastkami deformácie.
V prvom rade bolo cieľom preukázať, že správnou materiálovou charakteristikou pre konečnoprvkové modelovanie je skutočný pracovný diagram ocele. Z tohoto dôvodu boli vytvorené 2 simulácie – jedna s materiálovou charakteristikou (vstupom) v podobe technického diagramu (získaného z výsledkov ťahovej skúšky) a druhá v podobe skutočného diagramu (prepočítaného z technického diagramu pomocou logaritmických rovníc). Vzorky boli zaťažované len po pevnosť v ťahu (dosiahnutú pri Δx = 12,4 mm) a sledovaný bol vývoj plastických deformácií.
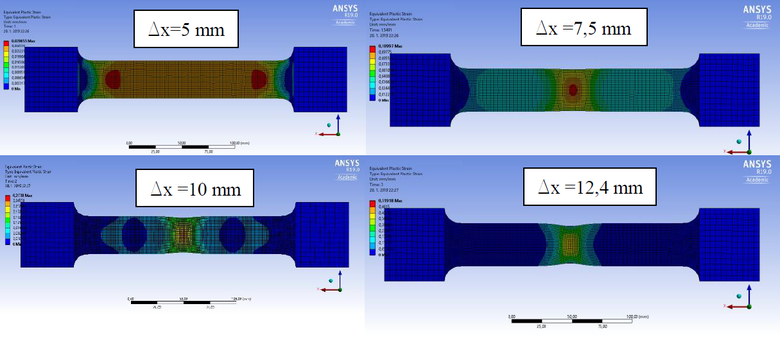
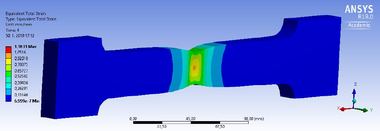
Obr. 5: Vývoj plastických deformácií pri použití technického pracovného diagramu ako materiálovej charakteristiky
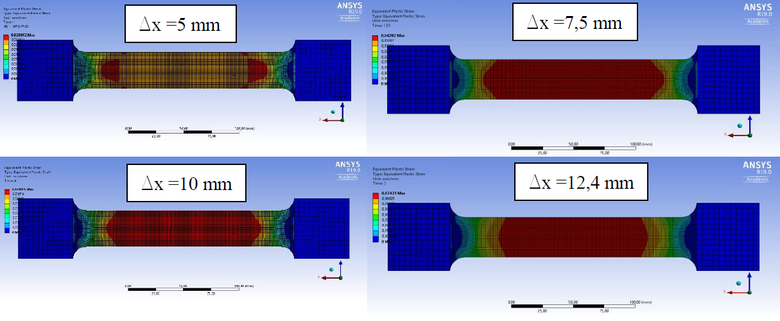
Obr. 6: Vývoj plastických deformácií pri použití skutočného pracovného diagramu ako materiálovej charakteristiky
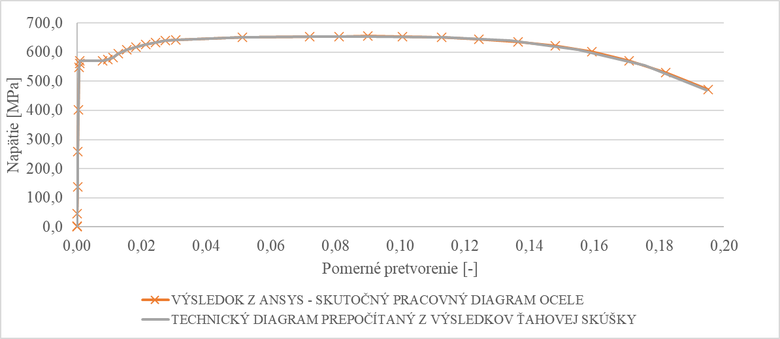
Výsledkami sa preukázalo, že použitím skutočného diagramu ocele je možné s vysokou presnosťou dosiahnuť pevnosť v ťahu (obr. 7) a plastické deformácie sú konštantné na meranej dĺžke (obr. 6). V prípade použitia technického diagramu ocele ako materiálovej charakteristiky v modeli, nielen že nie je možné dosiahnuť predpokladanú pevnosť v ťahu (obr. 7), ale aj plastické deformácie konečných prvkov nie sú konštantné na meranej dĺžke (vzniká krčok) (obr. 5), čo v oblasti po pevnosť v ťahu nie je korektné. V dôsledku vzniknutia krčku sú plastické pomerné pretvorenia konečných prvkov v danej oblasti viac ako 6násobné v porovnaní s predchádzajúcou simuláciou (obr. 7).
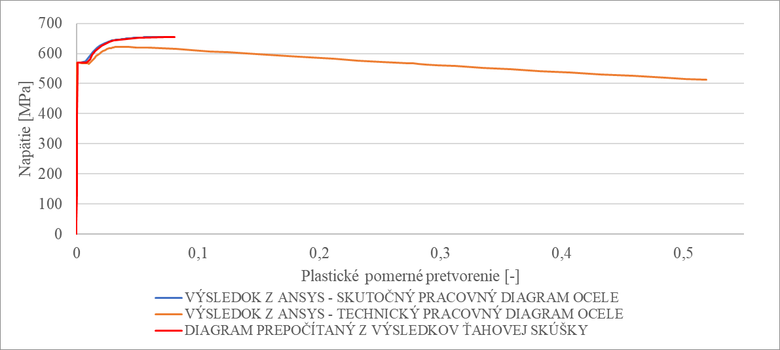
Obr. 7: Porovnanie materiálových parametrov ako vstupov do konečnoprvkových simulácií s výsledkom ťahovej skúšky
Následne bol výskum cielený na analýzu vplyvu typu a veľkosti konečných prvkov v oblasti diagramu, kde dochádza k vytváraniu krčku pri použití skutočného diagramu ocele. Je nutné uviesť, že pri každej zmene veľkosti, príp. typu konečného prvku treba vytvoriť nový skutočný diagram ocele. Vytvorené boli štyri modely s vyššie uvedenými parametrami konečných prvkov. Pri porovnaní jednotlivých diagramov získaných analýzou je zrejmé, že so zmenšujúcou sa veľkosťou prvkov rastie napätie a pomerné pretvorenie v diagrame, ako aj sklon samotnej krivky diagramu (obr. 8). V poslednej zo simulácií boli použité kvadratické elementy. Nakoľko tu bol najväčší počet uzlov prvkov (ale nie najväčší počet prvkov), celá tvorba skutočného diagramu trvala najdlhší čas. Hodnoty napätia a pomerného pretvorenia v porovnaní s rovnako veľkými lineárnymi elementami sú vyššie, avšak rozdiel je malý a krivky sú podobné.
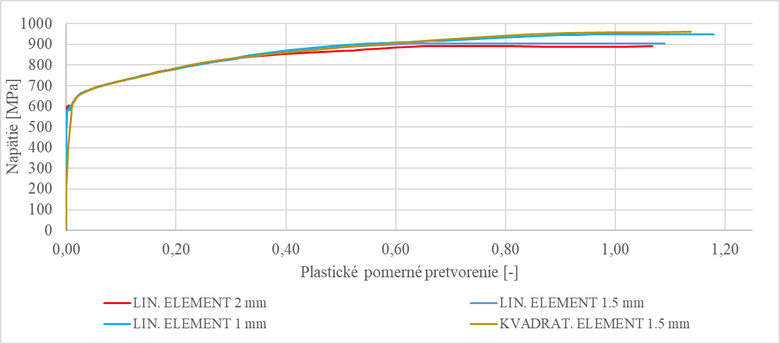
Obr. 8: Porovnanie výsledkov vo forme diagramov získaných prepočítaním výsledkov ťahovej skúšky a výsledkov zo softvéru ANSYS (hore), porovnanie skutočných pracovných diagramov pre jednotlivé typy a veľkosti konečných prvkov (dole)
4. Záver
Cieľom analýzy bolo preukázať, že v konečnoprvkovej analýze je použitie skutočného diagramu ocele správnym riešením. Prípadné použitie technického diagramu je nesprávne, Newton-Raphsonov algoritmus má problém s jeho klesajúcou vetvou a výsledky sú chybné. Technický diagram je však možné ľahko pretransformovať na skutočný diagram pomocou logaritmických vzorcov a napr. iteračnej metódy (v prípade použitia konečnoprvkových softvérov).
Veľkosť a typ konečných prvkov predstavujú parametre s veľkým vplyvom na priebeh skutočného diagramu ocele v oblasti tvorby krčku. So zvyšujúcou sa hustotou siete a s použitím kvadratických elementov rovnako rastie aj výpočtový čas. Z praktického hľadiska sa odporúča použiť takú veľkosť a typ konečných prvkov, ktoré dostatočne presne vystihujú geometriu riešeného telesa a výrazne nezvyšuje výpočtový čas. Je však nutné vedieť, že pre každú veľkosť a typ konečného prvku je pred simuláciou nutné vytvoriť nový skutočný diagram ocele.
5. Literatúra
- Gannon, L., 2011 Mesh Dependence of True Stress-Strain Curves in Finite Element Analysis of Steel Structures (DRDC Atlantic TM 2001-283; Defence R&D Canada – Atlantic) pp 1-20
- International Organization for Standardization, 2016 Metallic materials – Tensile testing – Part 1: Method of test at room temperature (ISO Standard No. 6892-1) retrieved from https://www.iso.org/standard/61856.html
- Ehlers, S., 2010 Strain and stress relation until fracture for finite element simulations of a thin circular plate, Thin-Walled Structures, vol. 48, pp 1-10
Computer simulations require appropriate input data to match the relevant calculated results with those of experiments. The true stress-strain curve suitable for finite element analysis is describing the non-linear behaviour of the steel with a proper relationship from beggining of loading to failure of the test specimen. The pre-peak part of the curve can be easily covered by an analytical method, but the necking part of the curve cannot be described by such a relationship between the normalized and the true stress-strain curves. Simple numerical tensile test of a steel specimen was performed to establish the true stress-strain curve in ANSYS software. Stress and strain from the computer analyses were compared with the results of the experimental tensile test.