Pruty z duplexní korozivzdorné oceli zatížené tlakem a ohybem
Příspěvek se zabývá chováním prutů z duplexní korozivzdorné oceli o otevřených svařovaných I-průřezech zatížených kombinací tlaku a ohybu k tuhé ose průřezu. Je uveden současný návrhový postup zmíněných prutů, včetně jeho nedostatků. Pro získání dat vystihujících reálné chování těchto prutů je popsána sada zhotovených zkoušek a numerický model vytvořený v softwaru Abaqus, včetně jeho validace. Dále je popsán vývin unikátního kloubového mechanismu pro provádění zkoušek prutů či prutových soustav.
1. Úvod
Konstrukce z korozivzdorné (nerezové) oceli jsou v současné době stále častěji využívány ve stavebnictví, a to zejména díky své odolnosti vůči korozi, estetickému vzhledu a mechanickým vlastnostem. Použití korozivzdorné oceli navíc vede k výraznému snížení nákladů na povrchovou úpravu jednotlivých konstrukčních prvků a na údržbu celé konstrukce během její životnosti, což je ale v porovnání s běžnou uhlíkovou ocelí vykoupeno několikanásobně vyšší pořizovací cenou. Obecně platí, že pro stavební využití jsou nejběžnější korozivzdorné oceli austenitické, feritické a austeniticko-feritické (duplexní). Volba příslušné třídy korozivzdorné oceli, kromě stupně odolnosti vůči korozi, ovlivňuje také svařitelnost, pevnost či houževnatost, resp. tažnost.
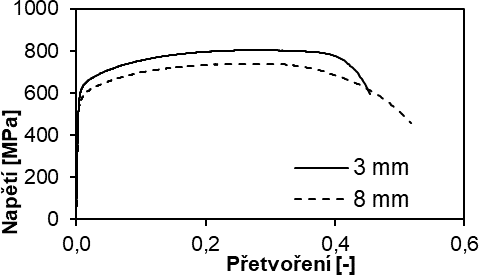
Materiálové vlastnosti korozivzdorné oceli se od uhlíkové oceli liší v řadě aspektů, jako je nelineární chování materiálu nebo absence jasně definované meze kluzu, jak je zřejmé z porovnání pracovních diagramů materiálů (viz Obr. 1). Na rozdíl od běžné uhlíkové oceli vykazují korozivzdorné (zejména austenitické či duplexní) oceli značnou míru plastického zpevnění a vysokou tažnost. Jak již bylo zmíněno, korozivzdorné oceli nemají jasně definovanou mez kluzu, proto se ve výpočtech používá smluvní mez kluzu, která odpovídá napětí při 0,2 % plastické deformace. Dalším rozdílem od uhlíkové oceli je, že korozivzdorná ocel mívá vyšší houževnatost, tedy že je odolnější vůči rázovému zatížení.
Z důvodů výše zmíněných rozdílů vlastností mezi uhlíkovou a korozivzdornou ocelí jsou pro návrhy prvků a konstrukcí z korozivzdorné oceli odvozeny odlišné návrhové postupy. Prezentovaný výzkum se zabývá konkrétně návrhem prutů o otevřených I-průřezech zatížených kombinací tlaku a jednoosého ohybu k tuhé ose průřezu. Příspěvek obsahuje stručné shrnutí problematiky navrhování zmíněných prutů, popis nově vyvinuté kloubové podpory potřebné k provedení nezbytných zkoušek, zhotovení experimentů a numerickou studii.
Obr. 1: Pracovní diagramy korozivzdorných ocelí a uhlíkové oceli (od 0 do 0,75 % deformace – vlevo; celý průběh pracovních diagramů – vpravo) [1]
2. Kombinace tlaku a ohybu dle Eurokódu
Eurokód 3 využívá k návrhu ocelových prutů zatížených kombinací tlaku a ohybu interakční rovnici vyjadřující součet využití prutu od zatížení tlakem (poměr tlakové síly ku vzpěrné únosnosti NED/Nb,Rd) a ohybem (poměr působícího ohybového momentu ku momentové únosnosti MED/MRd), které je upravené o vliv osové síly na ohybový moment. Zohlednění vlivu osové síly na ohybový moment je provedeno pomocí interakčního součinitele k, kterým se upraví velikost působícího ohybového momentu.
Návrhové postupy pro ocelové pruty z uhlíkové oceli jsou dány normou ČSN EN 1993-1-1 [2], která obsahuje dva možné postupy pro výpočet součinitele interakce uvedené v Příloze A a B známé také jako Metoda 1 a Metoda 2. Tyto postupy však nezaručují bezpečný a efektivní návrh prutů z oceli korozivzdorné. Proto byla vydána norma ČSN EN 1993-1-4 [3], která udává vztahy pro návrh prutů a konstrukcí z korozivzdorné oceli, včetně postupu pro posouzení únosnosti prutů namáhaných tlakem a ohybem. V tomto článku je uveden pouze postup pro kombinaci tlakové síly a jednoosého ohybu k tuhé ose průřezu. Podmínka spolehlivosti je dána vztahem (1) a interakční součinitel se má stanovit dle (2) ale zároveň splnit podmínku (3). Tento postup byl ale vyvinut před více než 10 lety na základě velmi malého množství dat a nezohledňuje některé významné faktory, jako například průběh momentu po délce prutu nebo náchylnost průřezu ke kroucení.
kde NED a MED jsou návrhové hodnoty tlakové síly a ohybového momentu, Nb,RD je vzpěrná únosnost prutu, eN,e je excentricita působící tlakové síly vůči těžišti průřezu, fy je mez kluzu, γM1 je materiálový součinitel spolehlivosti, βw,y = 1 pro průřezy 1. a 2. třídy, βw,y = Wel,y/Wpl,y pro průřezy třídy 3 a βw,y = Weff,y/Wpl,y pro průřezy třídy 4, ky je interakční součinitel a ![]() je poměrná štíhlost prutu.
je poměrná štíhlost prutu.
V posledních letech byla provedena řada studií zaměřených na chování prutů z korozivzdorných ocelí tvarovaných za studena [4], laserem svařované průřezy [5] nebo konvenčně svařované průřezy [6]. Stabilita prutů zatížených kombinací tlaku a ohybu byla zkoumána pro běžné tvary průřezu, jako jsou například I-průřezy [7], uzavřené čtvercové nebo obdélníkové průřezy [8]. Ve zmíněných studiích bylo prokázáno, že návrhový postup dle EN 1993-1-4 [3] vede k přehnaně konzervativním výsledkům a stále tedy zůstává prostor pro zlepšení návrhového postupu.
3. Kloubový mechanismus
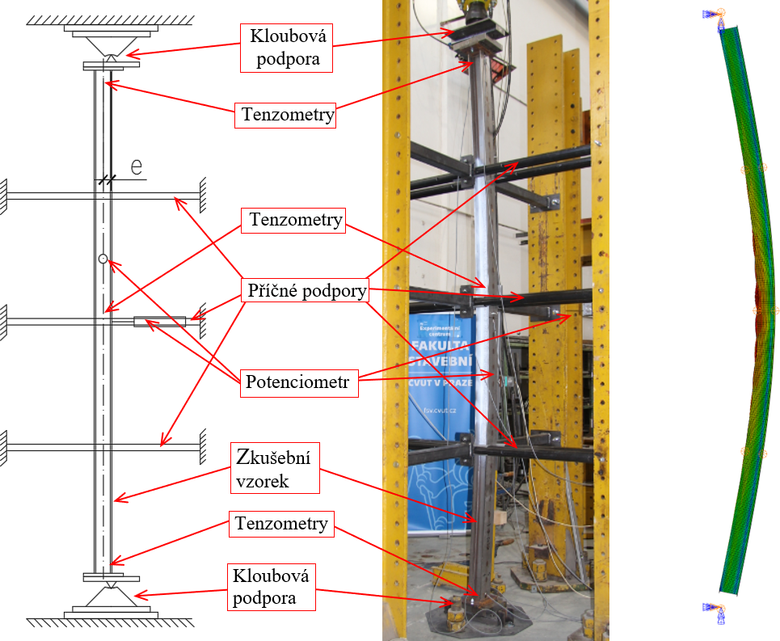
Doposud byly kloubové podpory tvořeny převážně kulovým nebo půlkulovým ložiskem, kde však dochází k významnému tření vedoucímu ke zkreslení výsledků experimentů. Dále není předem jasné, ve kterém směru dojde k vybočení zkoušeného prvku, zejména v případě prutu o dvojose symetrickém průřezu. Nově vyvinutá podpora má jasně definovaný bod, ve kterém bude přenášena vnitřní síla z prutu do podpory a bude umožňovat pouze jednoosé pootočení, díky čemuž bude dána rovina vybočení.
Během vývoje bylo nutné zohlednit rozměry samotných podpor v návaznosti na rozměry zkušebních vzorků a jejich připojení k podpoře. Vzhledem k faktu, že podpora je primárně určena pro ocelové pruty a prutové soustavy, předpokládalo se připojení pomocí patního plechu přivařeného ke konci kloubově ukládaného prutu. Spoj mezi patním plechem a kloubovou podporou bylo nutné navrhnout rozmontovatelný, aby kloubová podpora byla opakovatelně použitelná. Tento požadavek byl splněn pomocí šroubového spoje.
Kombinace požadavků na jasně definovaný bod a jednoosé pootočení vedlo na myšlenku liniové podpory. Aby bylo potočení možné, bylo nutné rozdělit podporu na dvě do sebe zapadající části, tzn. na část šroubově spojenou s patním plechem, která musela být schopna pootočení, a část, do níž byla první uložena. Obě části bylo nutné zhotovit z tuhých ocelových desek. K desce spojené s patním plechem byl z opačné strany přivařen ocelový klín tvořící liniovou podporu. Tento klín bylo nutné uložit do druhé ocelové desky tak, aby bylo umožněno pootočení a zároveň bylo zamezeno horizontálnímu posunu. Zmíněné podmínky byly zajištěny pomocí vyfrézované drážky tvaru „v“. Tato drážka ale musela svírat větší úhel než hrot klínu, kvůli prostoru nutnému pro jeho potočení.
Kloubová podpora má umožnit jak centrické, tak excentrické kloubové uložení vůči těžišti průřezu připojovaného prutu. Aby bylo možné nastavit libovolnou excentricitu, je nutné umisťovat šroubový přípoj v různých vzdálenostech od zmiňované osy. Tento problém byl vyřešen pomocí oválných otvorů v horizontálním směru, který zároveň dělá kloubový mechanismus velice univerzální. Oválné otvory navíc umožňuj rektifikaci polohy připojovaného prutu, a tím eliminují nejistotu nepřesného připojení patního plechu ke zkušebnímu vzorku. Deska s drážkou byla navíc vybavena otvory pro uchycení k podkladové desce a zamezení horizontálních posunů. Zhotovený kloubový mechanismus je zachycen na Obr. 2.
4. Experimentální studie
Pro zjištění chování prutů z korozivzdorné duplexní třídy oceli o otevřených svařovaných I-průřezech zatížených kombinací tlaku a ohybu k tuhé ose průřezu byla provedena sada zkoušek. Veškeré vzorky byly vyrobeny z plechů třídy EN 1.4462 o tloušťce 3 mm (stojina) a 8 mm (pásnice). Na oba konce zkoušeného prutu byly přivařeny patní plechy z uhlíkové oceli o tloušťce 15 mm. Před provedením zkoušky byl důkladně změřen skutečný rozměr a tvar zkoušených prutů, jelikož všechny výrobky z oceli vykazují počáteční geometrické lokální či globální odchylky (tzv. geometrické imperfekce) způsobené výrobním nebo montážním procesem. Skutečné rozměry jsou uvedeny v Tab. 1, kde h je výška průřezu, b je šířka průřezu, tf je tloušťka pásnice, tw je tloušťka stojiny, L0 je délka prutu (bez patních plechů), L je vzpěrná délka (L0 + tloušťky patních plechů a kloubového mechanismu), wg a wl jsou nevětší hodnoty amplitudy globální a lokální imperfekce.
| Vzorek | h [mm] | b [mm] | tw [mm] | tf [mm] | L0 [mm] | L [mm] | wg [mm] | wl [mm] |
|---|---|---|---|---|---|---|---|---|
| CS03-a | 97,73 | 99,49 | 2,97 | 7,99 | 3479 | 3639 | 11,71 | 0,71 |
| CS03-b | 98,26 | 99,89 | 2,97 | 8,07 | 3478 | 3638 | 6,34 | 0,41 |
| CS03-c | 98,17 | 100,16 | 2,97 | 8,12 | 3477,5 | 3637,5 | 6,50 | 0,42 |
| CS03-d | 98,28 | 100,13 | 2,97 | 8,11 | 3478,5 | 3638,5 | 7,05 | 1,16 |
| CS03-e | 98,09 | 99,93 | 2,97 | 8,02 | 3478 | 3638 | 5,76 | 0,29 |
| CS04-a | 117,64 | 120,00 | 2,97 | 7,97 | 3479 | 3639 | 4,86 | 0,44 |
| CS04-b | 117,90 | 119,86 | 2,97 | 7,96 | 3477 | 3637 | 3,83 | 0,38 |
| CS04-c | 118,05 | 120,02 | 2,97 | 8,09 | 3479,5 | 3639,5 | 4,85 | 0,62 |
| CS04-d | 117,37 | 119,84 | 2,97 | 7,97 | 3479 | 3639 | 3,72 | 0,60 |
| CS04-e | 117,57 | 119,50 | 2,97 | 7,98 | 3479 | 3639 | 3,84 | 0,42 |
| CS04-f | 117,61 | 119,86 | 2,97 | 8,00 | 3476 | 3636 | 4,34 | 0,39 |
Nejprve byly stanoveny materiálové vlastnosti korozivzdorné oceli. Tahové zkoušky byly provedeny podle předpisů stanovených v normě ČSN EN ISO 6892-1 [9]. Pro každou tloušťku byly vyrobeny 3 tahová zkušební tělesa. V průběhu zkoušky bylo zaznamenáno protažení vzorku pomocí mechanického extenzometru a dvou odporových tenzometrů, viz Obr. 3. Výsledné materiálové charakteristiky jsou uvedeny v Tab. 2, kde σ0,2 je napětí na mezi kluzu, σu napětí na mezi pevnosti, E0 je počáteční modul pružnosti, εu je poměrné přetvoření na mezi pevnosti a n a n‘0,2;1,0 jsou zpevňující parametry potřebné pro materiálové modely. Pracovní diagram byl uvažován dvoustupňový, dle Gardnera a Nethercota [10].
| t [mm] | σ0,2 [MPa] | σu [MPa] | E0 [MPa] | εu [–] | n [–] | n'0,2;1,0 [–] |
|---|---|---|---|---|---|---|
| 3 | 569,02 | 799,49 | 189 379 | 0,29 | 6,5 | 3,0 |
| 8 | 559,28 | 746,30 | 175 166 | 0,27 | 6,0 | 2,6 |
Celkem bylo vyzkoušeno 11 vzorků z duplexní korozivzdorné oceli zatížených kombinací tlaku a ohybu k tuhé ose průřezu. Sestava experimentu je znázorněna na Obr. 4. Všechny vzorky byly podepřeny proti vybočení ve směru měkké osy pomocí kruhových vodících trubek, rozepřenými mezi sloupy tuhého zkušebního rámu, osazenými plastovými kryty minimalizující tření mezi zkoušeným vzorkem a vodícími trubkami. Díky ohybu k tuhé ose a zmíněnému velmi malému tření byly horizontální síly působící na vodící trubky zcela zanedbatelné. V průběhu zkoušky byly zaznamenávány, s frekvencí 10 Hz, působící tlaková síla a průhyb sloupu, a to jak ve směru ohybu, tak ve směru kolmém. Pro měření průhybů byly použité strunové potenciometry, které byly umístěny v polovině výšky sloupu pro měření vybočení ve směru ohybu a v polovině vzdálenosti mezi vodícími trubkami pro vybočení z roviny. Pro stanovení skutečné excentricity síly byly použity odporové tenzometry připojené uprostřed každé pásnice v polovině výšky sloupou a v blízkosti patních plechů. Ve všech případech došlo ke ztrátě stability vlivem rovinného vzpěru s vybočením k tuhé ose průřezu.
5. Numerická studie
Numerický model byl zhotoven v softwaru Abaqus pomocí deskostěnových elementů S4R (Obr. 4) a následně byl validován pomocí dat získaných z provedených experimentálních zkoušek. Materiálové charakteristiky byly definovány dle dat z tahových zkoušek. Okrajové podmínky (podepření a zatížení) byly zavedeny pomocí referenčních bodů na obou koncích prutu, se kterým byly tuze propojeny, s příslušnou excentricitou vůči těžišti průřezu. Pruty byly modelovány na základě změřených rozměrů, a to včetně globální a lokální imperfekce. Dále bylo nutné zahrnout reziduální napětí způsobena výrobním procesem – svařováním. Předběžná validace numerického modelu byla provedena porovnáním závislosti tlakové síly na průhybu k tuhé ose průřezu. Typický výsledek validace je uveden na Obr. 5 (vlevo pro excentricitu zatížení 50 mm a vpravo pro centrický tlak). Je patrné, že výsledky numerického modelu jsou v dobré shodě se skutečným chováním zkoušeného prutu a model je tedy vhodný pro zhotovení následné parametrické studie.
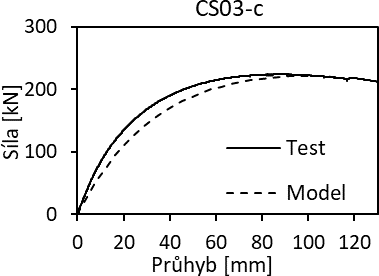
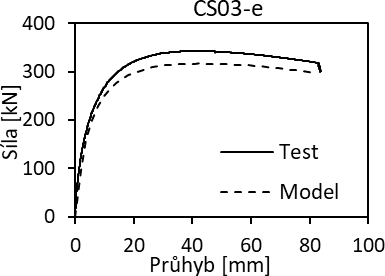
Obr. 5: Porovnání numerických a experimentálních výsledků
6. Závěr
Příspěvek se zabývá problematikou chování prutů z duplexní korozivzdorné oceli o otevřených svařovaných I-průřezech zatížených kombinací tlaku a jednoosého ohybu k tuhé ose průřezu. Byly popsány provedené experimenty, numerický model vytvořený v softwaru Abaqus a jeho úspěšná validace. Dále byl představen nový unikátní kloubový mechanismus vhodný pro provádění laboratorních zkoušek. V blízké době bude zhotovena numerická parametrická studie, díky které bude významně rozšířen soubor dat potřebných k ověření stávajících, případně vyvinutí nového návrhového postupu pro řešené pruty.
7. Literatura
- SCI Příručka pro navrhování konstrukcí z korozivzdorné oceli, Silwood Park, Ascot, Berks, SL5 7QN, UK, 2017
- ČSN EN 1993-1-1 Eurokód 3: Navrhování ocelových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby
- ČSN EN 1993-1-4 Eurokód 3: Navrhování ocelových konstrukcí – Část 1-4: Obecná pravidla – Doplňující pravidla pro korozivzdorné oceli
- JANDERA, M.; MACHAČEK, J. Residual stress pattern of stainless steel SHS, Tubular Structures, 2010
- BU, Y; GARDNER, L. Laser-welded stainless steel I-section beam-columns: Testing, simulation and design, Engineering Structures, 2019
- YUAN, H. & kol. Local–overall interactive buckling behaviour of welded stainless steel I-section columns, Journal of Constructional Steel Research 2015
- YANG, L. & kol. Member stability of stainless steel welded I-section beam-columns, Journal of Constructional Steel Research 2019
- ŽIDLICKÝ, B.; & JANDERA, M. Stainless steel SHS and RHS beam-columns, International Colloquium on Stability and Ductility of Steel Structures 2019
- ČSN EN ISO 6892-1 Kovové materiály – Zkoušení tahem – Část 1: Zkušební metoda za pokojové teploty
- GARDNER, L.; NETHERCOT, D.A. Experiments on stainless steel hollow section – Part 1: Material and cross-sectional behaviour, Journal of Constructional Steel research, 60, 2004, pp. 191-1318.
Poděkování
Tento výsledek byl realizován za finanční podpory z prostředků Technologické agentury České republiky (TAČR) v rámci projektu TJ04000272 „Návrh pokročilých konstrukcí z korozivzdorné oceli“.
Jedná se o aktuální téma, které reaguje na zvýšenou produkci korozivzdorné oceli a snahy o její efektivnější využití. Článek popisuje postup výzkumu chování tlačeného a ohýbaného sloupu, tzn. běžné konstrukce, který má vyústit ve výstižnější návrhový model, a tedy také lepší a hospodárnější využití materiálu korozivzdorné duplexní oceli.
Z odborného hlediska by bylo jistě přínosné v článku zmínit, zda byla během experimentu nějaká představa o tlakové síle v trubce, která bránila deformaci „na měkko“. Tzn., byla „smyková pružina“ daná třením a silou ve stabilizační trubce skutečně tak poddajná, že neovlivňovala deformaci na tuho... Z tohoto úhlu pohledu by bylo možné článek příště doplnit.
Text je strukturovaný stručně a logicky, použité výrazy jsou odborně korektní a text plně a jasně vystihuje záměr autorů výzkumu. Článek je jako celek kvalitní odborný text a doporučuji ho k vydání.
The paper deals with the behaviour of welded I-section duplex stainless steel members loaded by compression and major axis bending combination. The current beam-column design procedure is presented with its shortcomings described. To obtain the real behaviour data a set of conducted tests is presented, then numerical model created in Abaqus software with its validation is described. Furthermore, development of a unique pin-ended mechanism for member or member structure tests is given.
![Obr. 1a: Pracovní diagramy korozivzdorných ocelí a uhlíkové oceli (od 0 do 0,75 % deformace) [1]](/docu/clanky/0233/023304o2.png)
![Obr. 1b: Pracovní diagramy korozivzdorných ocelí a uhlíkové oceli (celý průběh pracovních diagramů) [1]](/docu/clanky/0233/023304o4.png)