Porovnání metodiky návrhu zesílení zděné ohýbané konstrukce
Článek se zabývá porovnáním metodiky návrhu zesílení zděné ohýbané konstrukce pomocí kompozitní výztuže s klasickými metodami zesílení. Žádná z dříve popsaných metod totiž neřeší problematiku zesílení ohýbaného cihelného nosníku na smyk, pokud nebude uvažována pouze smyková únosnost členěného ocelového průřezu. Této problematice vycházející z teorie příhradové analogie používané na zesílení ohýbaného železobetonového nosníku pomocí FRP tkanin či lamel nebo speciálních „L“ pásků se věnují teorie na zesílení železobetonových konstrukcí, kde je omezeno přetvoření aplikovaných FRP materiálů. Na obdobné teorii by mělo být možné stanovit i únosnost zesílené zděné konstrukce ve smyku.
1. Úvod
Problematikou zesilování zděných konstrukcí pomocí helikální výztuže se zabývala skupina vědců soustředěná kolem prof. RNDr. Ing. Petra Štěpánka, CSc. na konci 90. let minulého století a výsledkem byla zpráva popisující chování experimentálních prvků z cihelných nosníků zesílených helikální výztuží z roku 2001.
V rámci výzkumu zesilování železobetonových konstrukcí FRP lamelami proběhli na začátku 21. století v laboratořích experimentální zkoušky přímých cihelných kleneb zesílených FRP lamelou na spodním líci.
Mezi běžné způsoby zesílení cihelných ohýbaných nosníků patří i použití objímky z válcovaných L nosníků stažených plochou ocelí.
Žádná z výše popsaných metod neřeší však problematiku zesílení ohýbaného cihelného nosníku na smyk, pokud nebude uvažována pouze smyková únosnost členěného ocelového průřezu. Této problematice vycházející z teorie příhradové analogie používané na zesílení ohýbaného železobetonového nosníku pomocí FRP tkanin či lamel nebo speciálních „L“ pásků se věnují teorie na zesílení železobetonových konstrukcí, kde je omezeno přetvoření aplikovaných FRP materiálů. Na obdobné teorii by mělo být možné stanovit i únosnost zesílené zděné konstrukce ve smyku.
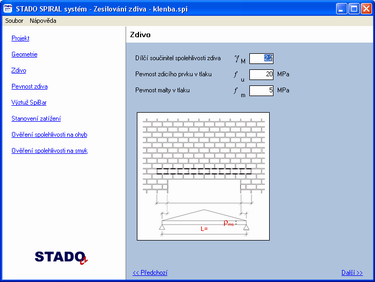
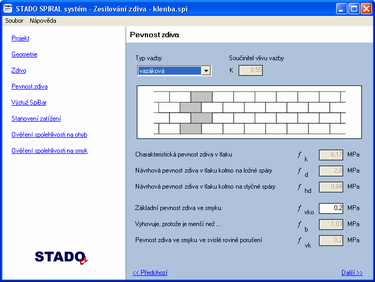
2. Výpočet kapacity průřezu pro zdivo
moment únosnosti zesíleného zděného průřezu
rameno vnitřních sil vyztuženého zděného průřezu
kde je
- b
- … šířka průřezu,
- d
- … účinná výška průřezu
- As
- … průřezová plocha jakékoliv zesilující výztuže (běžná betonářská, helikální, FRP výztuž apod.)
- fk
- … charakteristická pevnost zdiva ve směru působícího normálového napětí
- fyk
- … charakteristická pevnost zesilující výztuže(běžná betonářská, helikální, FRP výztuž apod.)
- γs , γM
- … dílčí součinitele spolehlivosti pro zesilující výztuž, resp. zdivo
3. Kontrola kotevní oblasti a omezení protažení zesilující výztuže
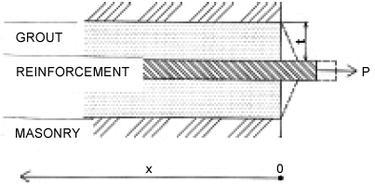
Obr. 1 Schéma kotevní oblasti.
Pro stanovení deformace a napjatosti lze na zjednodušeném modelu kotevní oblasti odvodit jednoduchou diferenciální rovnici. Schéma modelu kotevní oblasti pro analytické řešení je uvedeno na obr. 1. Při odvození diferenciální rovnice popisující problematiku kotevní oblasti vycházíme z předpokladů lineárně pružného chování materiálů a platnosti teorie malých deformací v případě rovinné napjatosti. Dále vycházíme z předpokladu, že zálivka přenáší pouze smyková napětí, a z předpokladu nekonečné tuhosti zdiva, tzn. že zdivo se nedeformuje. Z uvedených předpokladů lze odvodit homogenní diferenciální rovnici pro posun výztuže:
(1)
kde je
- Ev (Ez)
- … modul pružnosti výztuže (zálivky),
- o
- … obvod povrchu výztuže,
- Av
- … průřezová plocha výztuže,
- t
- … tloušťka zálivky
- μz
- … Poissonův součinitel zálivky.
Řešení rovnice (1) nalezneme ve tvaru:
(2)
kde
Normálové napětí ve výztuži σv(x) a smykové napětí v zálivce τxz(x) lze vypočítat ze vztahů:
(3)
Ve vztazích (2) a (3) jsou C1 a C2 neznámé integrační konstanty, které lze určit z okrajových podmínek, které předpokládáme ve dvou variantách:
a) varianta A
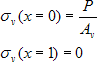
Druhá okrajová podmínka vychází z předpokladu, že známe délku kotevní oblasti l. Tím jsme dostali dvě na sobě nezávislé lineární rovnice pro neznámé C1 a C2. Lze odvodit:
b) varianta B
První okrajová podmínka zůstane stejná jako ve variantě A. Na konci kotevní oblasti musí platit podmínka:
což je ekvivalentní – vzhledem ke tvaru obecného řešení – podmínce
Řešením získáme
Experimenty byla prokázána nejmenší kotevní délka výztuže v drážce ve zdivu i betonu resp. ve vrtu viz technické listy dodavatele technologie (např. www.STADO.CZ).
Obr. 2 Pohled na zkušební rám.
Byly vyzděny zkušební vzorky z plných cihel do zkušebního rámu a postupně vlepovány do drážky nebo vrtu zkušební vzorky jednotlivých profilů, resp. pro zkoušky soudržnosti s betonem byly do vybetonovaného vzorku vyvrtány otvory nebo vyfrézovány drážka a do ní nebo vrtu vložen předepsaný profil.
| Materiál | Tahová síla [kN] | Kotevní délka [mm] | Průměr výztuže-Spibar [mm] |
|---|---|---|---|
| Beton-C20/25 | 7,52 | 250 | 6 |
| Plná cihla | 7,99 | 450 | 6 |
| Materiál | Tahová síla [kN] | Kotevní délka [mm] | Průměr výztuže [mm] |
|---|---|---|---|
| Beton-C20/25 | 8,27 | 150 | 6 |
| Plná cihla | 4,41 | 80 | 8 |
4. Příklad výpočtu zesílené konstrukce FRP lamelou
Obr. 3 Schéma zesílené přímé klenby FRP lamelou.
Pro simulaci zesílení cihelné klenby byly vyrobeny tři zkušební prvky z cihelného zdiva rozměrů 290 × 140 × 1715 mm z cihel CP 25 na maltu MVC 10, jenž byly zesíleny pomocí jedné CFK lamely Sika® CarboDur® S 512 50 / 1,2 / 1700 mm na spodním povrchu nosníku, Epoxi-lepidlo Sikadur®-30.
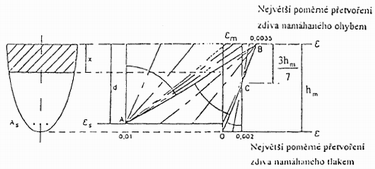
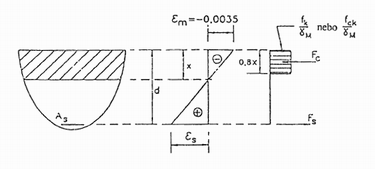
Obr. 4, 5 Rozdělení poměrné deformace, resp. napětí a vnitřních sil u vyztuženého cihelného průřezu.
4.1. Stanovení zatížitelnosti zesílené přímé klenby
Materiálové charakteristiky zdiva:
charakteristická pevnost v tlaku nevyztuženého zdiva s obyčejnou maltou:
kde
fb = 25 N/mm2,
fm = 10 N/mm2
modul pružnosti:
a) v ohybu E = αsec . fk = 1000.7,925 = 7925 MPa
b) ve smyku G = 0,4E = 3170 MPa
charakteristická pevnost ve smyku nevyztuženého zdiva:
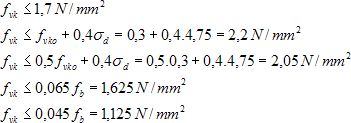
dílčí součinitel spolehlivosti materiálu:
γM = 2,2 pro kategorii provádění B a kategorii kontroly výroby zdících prvků I.
Návrhové hodnoty pevnosti zdiva:
v tlaku 
ve smyku 
, 
EL = 155 GPa
γl = 1,2
Návrhový ohybový moment:
nevyztuženého nosníku:
kde je
- fxk
- … charakteristická pevnost zdiva v ohybu fxk = 0,24 MPa
- Z
- … průřezový modul
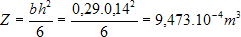
maximální rovnoměrné zatížení:
reakce: 
zesíleného nosníku:
maximální výška tlačené oblasti zdiva:
tlaková síla: 
rameno vnitřních sil:
moment únosnosti:
zatěžovací síla: 
reakce: 
Smyková únosnost zesíleného nosníku:
a) uvažuji nevyztužený nosník:
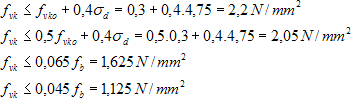zvolena nejmenší z hodnot.
kde je
- t
- … tloušťka zdiva
- lc
- … výška tlačené oblasti zdiva ve smyku, 0,3 d = 0,3 . 0,14 = 0,042 m
b) uvažuji vyztužený nosník:
uvažována max. možná hodnot fvk
kde je
- b
- … nejmenší šířka prvku příslušející účinné výšce
Experimentální únosnost: Vd,exp = VRd1 . γexp = 9 . 2 = 18 kN
O porušení prvku rozhoduje únosnost ve smyku!
| Nosník C1 | Nosník C2 | Nosník C3 | Průměr | |
|---|---|---|---|---|
| Naměřená síla [kN] | 19 | 20 | 23 | 20,66 |
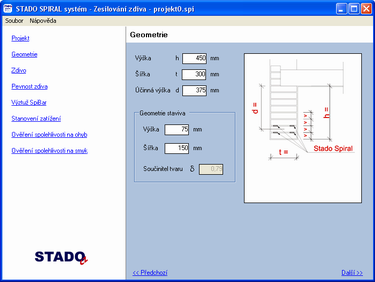
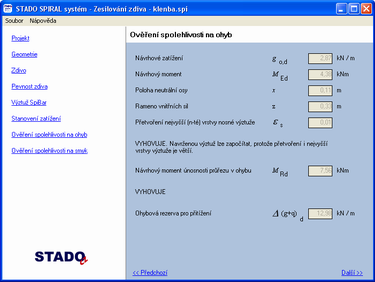
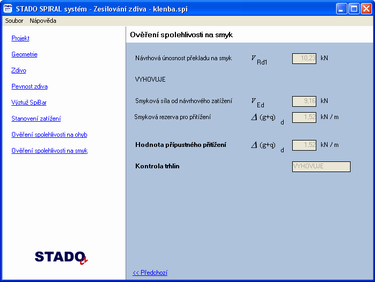
4.2. Zesílení zděného průřezu na ohyb dle EC programem STADO Spiral
Kapitola 4.2 dokumentuje možnost návrhu zesílení zděného přímého ohýbaného nosníku pomocí helikální výztuže, lze i pomocí libovolné výztuže (skleněné, betonářská výztuž, FRP výztuž) tvořícího překlad nad otvorem ve veřejně přístupném programu firmy STADO CZ s.r.o., který je každý schopen získat z webové stránky firmy. Jako omezující podmínka se ve většině případů jeví únosnost nosníku na smyk, pokud není na toto namáhání nosník dodatečně zesílen nějakou výztuží.
5. Posudek členěného nosníku na ohyb
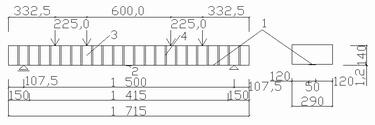
Jako vzorový nosník byl zvolen prostý nosník rozpětí 1,5 m a modelováno zatížení tohoto nosníků rozdělené na ostatní stálé a užitné, prut tvořen 4 profily L 60/60/5, které vytváří členěný profil 400×400 mm spojený rámovými spojkami z pásové oceli 30×3 mm a´ = 200 mm.
Pro posouzení použit program FIN 2D EC.
ZS1 vlastní tíha 4xL60/60/5
ZS2 ostatní stálé
ZS3 užitné
Deformace ZS1+ZS2+ZS3
Vnitřní síly ZS1+ZS2+ZS3
Posudek členěného průřezu
Posudek proveden za předpokladu zanedbání smykové a ohybové únosnosti zdiva!
6. Otázkou tedy do budoucna je: co se stane aplikací tkaniny na smykem namáhaný cihelný nosník?
Bude možno jen upravit teorii používanou pro zesílení tkaninou na betonový nosník.
Příspěvek FRP materiálu k únosnosti ve smyku, Vfd, „uvažováno zesílení svislou tkaninou“
Např. Efu = GPa, tloušťky tf = m, εfd,e = (technický list dodavatele), aplikovanou pod úhlem α = 90°, tj. svisle.
kde únosnost FRP výztuže se výpočte podle vzorce:
kde je
- εfd,e
- … konstrukční parametr efektivní FRP deformace
- bw
- … minimální šíře příčného řezu nad efektivní hloubkou
- d
- … efektivní výška příčného řezu
- ρf
- … FRP stupeň vyztužení rovný 2tf . sinα / bw pro šikmý řez smyková výztuž tloušťky tf
(bw = minimální šíře betonového příčného řezu nad efektivní výškou), nebo
(2tf / bw) . (bf / sf) pro FRP výztuž ve formě tkaniny nebo pásků tkaniny šíře bf v rozestupu sf - Efu
- … moduly pružnosti FRP ve směru orientace vláken
- θ
- … úhel úhlopříčné šikmé smykové trhliny od roviny, většinou převzat rovný 45°
- α
- … úhel mezi směrem vláken a rovinou
Navrhovaná hodnota pro beton je εfd,e = 0,004, resp. lze nalézt limitní hodnotu poměrné deformace i v technických listech dodavatelů FRP tkanin nebo lamel.
7. Teorie pro posouzení vyztuženého zdiva betonářskou výztuží
U vyztužených zděných stěn se svislou výztuží při uvážení vlivu smykové výztuže se musí prokázat, že:
kde
kde je
- fvd
- … menší z hodnot návrhové pevnosti ve smyku buď zdiva nebo výplňového betonu, kde fvd ≤ 0,3 MPa
- b
- … nejmenší šířka nosníku v místě, kde se pro výpočet stanovuje účinná výška průřezu
- d
- … účinná výška průřezu
U vyztužených zděných stěn se svislou výztuží při uvážení vlivu smykové výztuže se musí prokázat, že:
kde fd je menší hodnota buď návrhové pevnosti zdiva v tlaku nebo výplňového betonu.
kde je
- d
- … je účinná výška nosníku
- Asw
- … průřezová plocha smykové výztuže
- s
- … vzdálenost prutů smykové výztuže
- α
- … úhel sklonu výztuže od osy nosníku mezi 45° a 90°
- fyd
- … návrhová hodnota pevnosti smykové výztuže
8. Závěr
V následujícím roce by skupina kolem prof. Ing. Jiřího Witzanyho, DrSc., chtěla v rámci grantu NAKI prokázat na experimentálních vzorcích přímých kleneb zesílených FRP tkaninami, resp. FRP lamelami, zdali je možno obdobnou teorii, kterou známe z železobetonových nosníků uplatnit i na nosnících cihelných, předpokládáme redukci poměrné deformace v tkanině v poměrů modulů pružností betonů a zdiva tj. běžně 3–5 GPa (zdivo)/ 27–33 GPa (beton) = 1/9 až 1/6.
εfd,e = 0,00044 až 0,0006.
Poděkování
Výsledky uvedené v článku byly získány v rámci řešení projektu NAKI DF12P01OVV037 „Progresivní neinvazivní metody stabilizace, konzervace a zpevňování historických konstrukcí a jejich částí kompozitními materiály na bázi vláken a nanovláken“ poskytnutého Ministerstvem kultury ČR.
Literatura
- [1] ČSN EN 1996-1-1 Navrhování zděných konstrukcí – Část 1-1: Obecná pravidla pro vyztužené a nevyztužené zděné konstrukce.
- [2] ČSN EN 1992-1-1 Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby.
- [3] Externally bonded FRP reinforcement for RC structures Technical report on the “Design and use of externally bonded fibre reinforced polymer reinforcement (FRP EBR) for reinforced concrete structures” by 'EBR' working party of fib TG 9.3, July 2001, 138 pp.
- [4] Problematika zesilování zděných konstrukcí dodatečně vkládanou výztuží, Doc. RNDr. Ing. Petr Štěpánek, CSc. + kol., Brno 2001.
This paper describes the method for calculating the amplification of curved brick construction with composite reinforcement and compares this procedure with reinforcement made by conventional methods to gain a practical demonstration of the bent beam.
