Únosnost spojů s ocelovými úhelníky
Cílem článku je popsat návrh ocelových úhelníků v dřevěných spojích. Návrh nemá dostatečnou oporu v existujících normách. Článek uvádí experimenty, výpočetní modely a zjednodušené výpočty podle norem. Rozdíly mezi nimi ukazují, jak složité je navrhovat dřevěné spoje s trojrozměrným kováním.
1. Úvod
V dnešní době se u dřevostaveb uplatňují spoje s kováním, které mají některé výhody oproti tesařským spojům (neoslabení spojovaných prvků, rychlost provedení). K dalším výhodám patří možnost aplikace přímo na stavbě nebo přímé napojení na ocelové či betonové konstrukce. Mezi kování patří desky s prolisovanými trny, úhelníky, třmeny, spojovací desky, kotevní prvky apod. Pro výpočet únosnosti spojů s kováním lze částečně použít normu 1995-1-1: Eurokód 5 (EC 5) [1]. Tato norma se zaměřuje převážně na samotné chování spojovacích prostředků a neposkytuje dostatečnou podporu pro návrh spoje s kováním, kde únosnost závisí např. i na chování samotného kování. Spoje jsou často namáhány ve více směrech. Spojovací prostředky jsou tedy namáhány ve smyku i na vytažení. K tomu dochází také u jednosměrného namáhaní vlivem páčení. Hlavním problémem těchto spojů je jejich poddajnost. Ta je zapříčiněna především velkou deformací ocelového kování, ale také zatlačováním hřebíků do dřeva a jejich vytahováním. Při návrhu spojů s kováním by se nemělo na tyto skutečnosti zapomínat. Zvláště u spojů, kdy o únosnosti celého spoje rozhoduje únosnost hřebíků na vytažení. Od okamžiku vyčerpání únosnosti hřebíku na vytažení dochází k velkému nárůstu deformace.
2. Materiál a hřebíky
Tento článek se zaměřuje na jeden typ kování tzv. úhelníky. Úhelníky jsou z pozinkovaného ocelového plechu. Ve výpočtech a modelech je uvažováno dřevo třídy C24 podle normy EN 338 [2]. Pokud dřevo použité během experimentu nespadá do třídy C24, jsou hodnoty únosnosti přepočítány podle EOTA TR16 [3]. Hřebíky jsou kroužkové délky 60 mm a průměru 4 mm. Na základě zkoušek je znám pracovní diagram hřebíků na vytažení i maximální únosnost v osovém směru. Ze zkoušek spoje ocel dřevo v tahu je znám pracovní diagram hřebíku ve střihu a podle Eurokódu 5 je určena jeho maximální únosnost ve střihu.




 Obr. 1 Zkoušené úhelníky (úhelník s vlisem, úhelník bez vlisu, úhelník s pravidelnými roztečemi, valbový úhelník, úhelník s křidélky)
Obr. 1 Zkoušené úhelníky (úhelník s vlisem, úhelník bez vlisu, úhelník s pravidelnými roztečemi, valbový úhelník, úhelník s křidélky)3. Zjednodušený výpočet podle EC 5
Zjednodušený výpočet únosnosti spojů s úhelníky byl proveden podle normy EC 5. Celková únosnost spoje je dána únosností spojovacích prostředků ve střihu a na vytažení. Při únosnosti ve střihu vstupuje do výpočtu vedle počtu spojovacích prostředků i tzv. efektivní počet. Problémem je, že tento výpočet nebere v úvahu např. páčení nebo deformaci úhelníku.
4. Experimenty
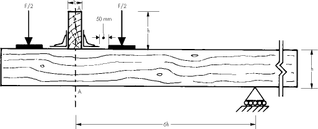
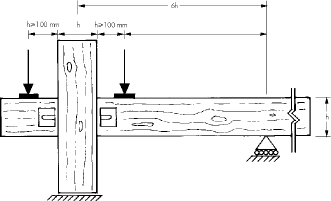
Byly provedeny dva typy experimentů. V prvním případě bylo zatěžováno tak, že hřebíky jedné větve úhelníku byly vytahovány a hřebíky druhé větve byly namáhány na střih (obr. 2). Tento způsob namáhání je nazýván směrem 1. Takto bylo odzkoušeno 8 typů úhelníků (3 úhelníky s vlisem, 3 úhelníky bez vlisu a 2 úhelníky s pravidelnými roztečemi) vždy po pěti zkouškách. V druhém případě (směr 2) bylo zatěžováno tak, že hřebíky obou větví byly namáhány na střih (obr. 2). Takto byly odzkoušeny tři typy úhelníků (úhelník s vlisem, valbový úhelník a úhelník s křidélky) po pěti zkouškách. Zkoušky ve směru 1 i 2 byly provedeny podle normy ČSN EN 26891 [4] a technické zprávy EOTA TR16 v laboratořích UCEEB při ČVUT. Během zkoušky byla měřena deformace mezi dřevěnými prvky.
Podle normy ČSN EN 26891 a ETAG 015 [5] je maximální síla dána destrukcí spoje nebo deformací 15 mm. Ve směru 1 u vzorků s úhelníky s vlisem a s úhelníky bez vlisu došlo k destrukci dříve než při 15 mm. Jako maximální síla byla u úhelníků s pravidelnými roztečemi určena hodnota, kdy se zvyšovala deformace bez přírůstku síly. Tato situace nastala, když byla vyčerpána únosnost první řady hřebíků na vytažení. Ve směru 2 byla pro úhelníky s vlisem a valbové úhelníky určena maximální síla jako hodnota při deformaci 15 mm. U zkoušek úhelníku s křidélky byla zkouška ukončena při deformaci okolo 9 mm a maximální síla mohla být určena pro deformaci 8 mm. Charakteristická únosnost spoje byla určena podle normy ČSN EN 14358 [6] a EOTA TR16.
5. Numerický výpočetní model
Numerické výpočetní modely byly vytvořeny v programu RFEM. Materiál úhelníků byl definován pracovním diagramem použité oceli S280GD + Z275. Byl zvolen izotropní plastický model. Ve směru 1 jsou 2D modely úhelníků tvořeny prutovými prvky. U úhelníků s prolisem je moment setrvačnosti prutů proměnný v závislosti na geometrii prolisu. V místech předpokládaného vzniku plastických kloubů jsou vytvořeny klouby s danou rotační tuhostí. Pracovní diagramy rotační tuhosti plastických kloubů byly určeny pro jednotlivé průřezy v programu ANSYS. Podporami úhelníku jsou hřebíky a samotný dřevěný prvek. Hřebíky jsou zadány pomocí podpor s tuhostmi, které odpovídají pracovním diagramům na vytažení a ve střihu. Dřevěný prvek je simulován jako podloží úhelníku. Pomocí tlakových materiálových zkoušek smrkového dřeva třídy C24 byl získán pracovní diagram a byla stanovena hodnota tuhosti. Pro směr 2 byly modely úhelníků trojrozměrné.
6. Závěr
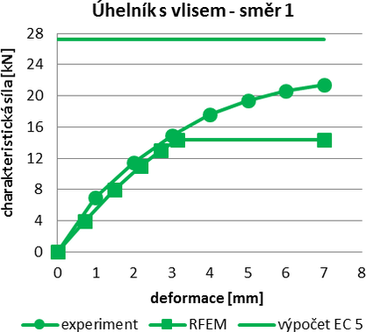
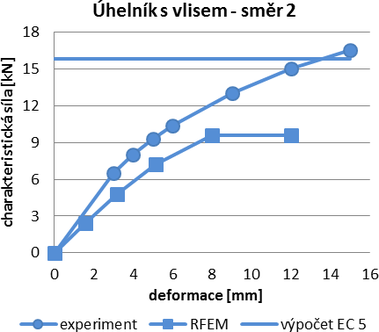
V praxi se často používá zjednodušený výpočet podle Eurokódů. Tento výpočet se často zaměřuje pouze na spojovací prostředky (hřebíky, vruty, svorníky). Neuvažuje rozložení zatížení, páčení či deformaci úhelníku. Vypočtené maximální únosnosti jsou mnohem vyšší než únosnosti získané z experimentů. Rozdíl je větší pro úhelníky bez vlisu, které mají nižší tuhost. To může být v praxi nebezpečné. Projektanti by měli brát v úvahu specifika těchto spojů, ale ruční výpočet je z hlediska složitosti a časové náročnosti nereálný. Pro projekční praxi je vhodné použít návrhové tabulky výrobce, nebo experimentálně ověřené výpočetní modely pro daný typ spoje. Na obr. 3 je vidět rozdíl pro dva různé úhelníky s vlisem mezi únosnostmi získanými zjednodušeným výpočtem podle EC 5, experimenty a modely RFEM.
Poděkování
Tato práce vznikla za finanční podpory MŠMT v rámci programu NPU I č. LO1605 – Univerzitní centrum energeticky efektivních budov – Fáze udržitelnosti.
7. Literatura
- ČSN EN 1995-1-1 Eurokód 5: Navrhování dřevěných konstrukcí – Část 1-1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby. ČNI, 2006, Praha.
- ČSN EN 338 Konstrukční dřevo – Třídy pevnosti. ÚNMZ, 2010, Praha.
- EOTA TR 16: Method of testing Three-Dimensional Nailing Plates with examples, October 2012.
- ČSN EN 26891 (73 2070) Dřevěné konstrukce – Spoje s mechanickými spojovacími prostředky – Všeobecné zásady pro zjišťování charakteristik únosnosti a přetvoření, ČNI, 1994, Praha.
- ETAG 015: Three-Dimensional Nailing Plates, November 2012.
- ČSN EN 14358: Dřevěné konstrukce – Dřevěné konstrukce – Výpočet a ověřování charakteristických hodnot, ÚNMZ, Praha, 2017.
The aim of this study is to describe the design of steel angle brackets in timber joints. The design has insufficient support in the existing standards. This article shows experiments, computational models and calculations according to the standards. The differences between them indicate the difficulty of designing timber joints with three-dimensional nailing plates.