Analýza modelu tesařského spoje
Předmětem tohoto článku je porovnávání numerických prostorových modelů tesařského spoje, konkrétně kolmého lípnutí. Numerický model tohoto tesařského spoje zahrnuje i materiálové nelinearity. Materiálový model dřeva předpokládá pružno-plastické a ortotropní – transverzálně isotropní chování dřeva. Konečněprvkové sítě se od sebe liší použitými prvky a jejich počtem, mapováním a lokálním zahuštěním sítě. Autoři sledovali počty uzlových bodů a prvků, rychlost konvergence výpočtu, přesnost řešení, symetrii a mapování prvků.
1 Úvod
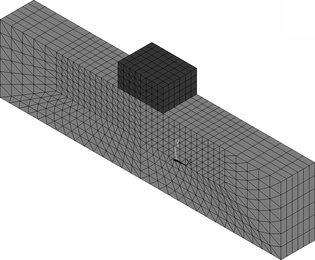
Tento článek se zaměřuje na zkoumání tesařského spoje, a to konkrétně kolmého lípnutí. Spoj je složen ze dvou konstrukčních prvků – jednoho podélného a druhého příčného, viz obr. 1. Spojení lípnutím bývá obvykle zajištěno tesařskou skobou. Příčný konstrukční prvek je namáhán tlakem rovnoběžně s vlákny dřeva. Podélný konstrukční prvek je pak namáhán tlakem kolmo k vláknům dřeva.
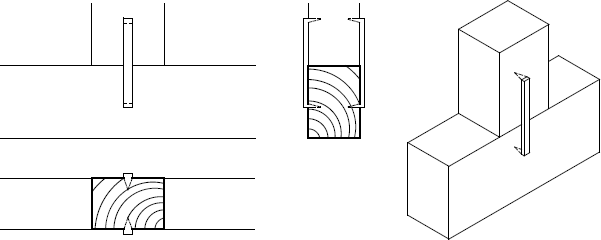
Obr. 1. Tradiční tesařský spoj – kolmé lípnutí
Pevnost dřeva v tlaku kolmo k vláknům je výrazně nižší než pevnost v tlaku rovnoběžně s vlákny. Pro nejběžnější pevnostní třídu konstrukčního dřeva v České republice, značenou C24, jsou v normě ČSN EN 338 [1] uvedeny tyto charakteristické pevnosti dřeva:
kde fc,0,k je charakteristická pevnost dřeva v tlaku rovnoběžně s vlákny a fc,90,k je charakteristická pevnost dřeva v tlaku kolmo k vláknům. S ohledem na téměř desetinásobný rozdíl těchto charakteristických pevností dochází často v podélném prvku k překročení hodnoty pevnosti v tlaku kolmo k vláknům dřeva, a tím k nežádoucím lokálním deformacím (stlačení) tohoto prvku.
2 Konečněprvková síť modelu
Článek se zaměřuje na 21 numerických modelů tesařského spoje. Všechny výpočty jsou provedeny na stejném počítači, jehož hardware se skládá z CPU Intel Xeon E5-1650, 6 jader 3,2 GHz, RAM 16 GB. Numerické modely jsou vytvořeny v softwaru ANSYS 16.0, Academic. Všechny vstupní parametry, kromě konečněprvkové sítě, jsou ve všech zkoumaných numerických modelech stejné.
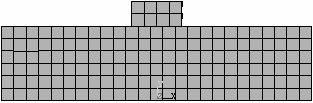
1_1
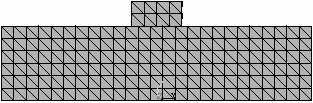
1_2
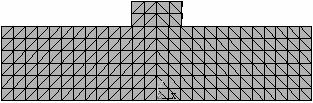
1_3
1_4
1_5
1_6
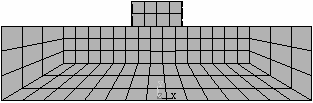
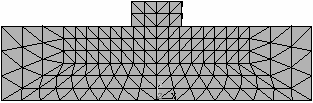
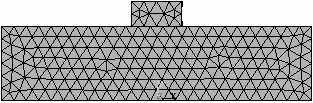
Obr. 2. Analyzované konečněprvkové sítě a jejich označení
Numerický model tradičního tesařského spojení – kolmého lípnutí obsahuje ortotropní pružno-plastické materiálové chování dřeva. Tento materiálový model předpokládá bilineární průběh poměrného přetvoření dřeva, viz Moses a Prion [2]. Obr. 2. uvádí různé typy konečněprvkových sítí a jejich označení. Jednotlivé sítě se od sebe liší typem, velikostí a počtem použitých elementů. Prvky SOLID45 a SOLID95 jsou použity pro mapovanou konečněprvkovou síť, kdežto prvek SOLID92 tvoří nemapovanou (free) síť. Použité prvky jsou znázorněny na obr. č. 3.
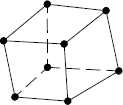
SOLID45 hex
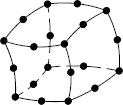
SOLID95 hex
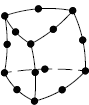
SOLID95 pent
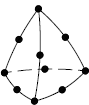
SOLID92 tetr
Obr. 3. Použité typy elementů
Tab. 1 prezentuje procentuální shodu výsledku jednotlivých typů konečněprvkových sítí s nejpřesnějším numerickým výsledkem a časy konvergence výpočtu. Hodnoceným výsledkem je velikost tlakové síly při svislém posunu 25 mm. U modelů 1_6_1 a 1_6_2 výpočet nekonverguje, a proto jsou uváděny časy pro 30 % 1 a 42 % 2 celkového výpočtu. Poslední číslice v označení sítí představuje délku hrany nejmenšího prvku (1 pro 20 mm, 2 pro 10 mm a 3 pro 5 mm). Modely se sítěmi 1_6_1 a 1_6_2 nejsou hodnoceny vzhledem k nekonvergenci numerického výpočtu.
| Číslo sítě | 1_1_1 | 1_1_4 | 1_2_1 | 1_3_1 | 1_4_1 | 1_5_1 | 1_6_1 |
| Kvalita [%] | 75 | 106 | 102 | 103 | 106 | 101 | – |
| Čas výpočtu | 0:00:15 | 0:00:48 | 0:00:49 | 0:00:48 | 0:00:29 | 0:00:37 | 0:00:21 1 |
| Číslo sítě | 1_1_2 | 1_1_5 | 1_2_2 | 1_3_2 | 1_4_2 | 1_5_2 | 1_6_2 |
| Kvalita [%] | 93 | 101 | 101 | 101 | 101 | 100 | – |
| Čas výpočtu | 0:01:46 | 0:08:11 | 0:09:03 | 0:08:13 | 0:04:25 | 0:04:57 | 0:06:20 2 |
| Číslo sítě | 1_1_3 | 1_1_6 | 1_2_3 | 1_3_3 | 1_4_3 | 1_5_3 | 1_6_3 |
| Kvalita [%] | 98 | 100 | 100 | 100 | 100 | 100 | 100 |
| Čas výpočtu | 0:22:01 | 5:58:24 | 5:03:21 | 5:18:57 | 2:14:44 | 1:53:31 | 18:39:58 |
3 Symetrie numerického modelu
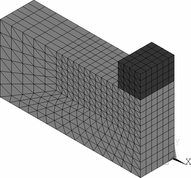
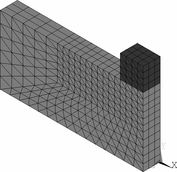
K urychlení výpočtu je využito symetrie modelu tesařského spoje. Na obr. 4. je vidět porovnání celého, polovičního a čtvrtinového modelu 1_5_2. Poloviční a čtvrtinový model využívá symetrie celého modelu podle jedné resp. dvou rovin. Při využití dvou rovin symetrie je výpočet více než 6× rychlejší než model bez využití symetrie viz tab. 2.
| Označení modelu | 1_5_1 | 1_5_1_symm2 | 1_5_2_symm2 |
| Čas výpočtu [hh:mm:ss] | 0:05:30 | 0:02:45 | 0:00:51 |
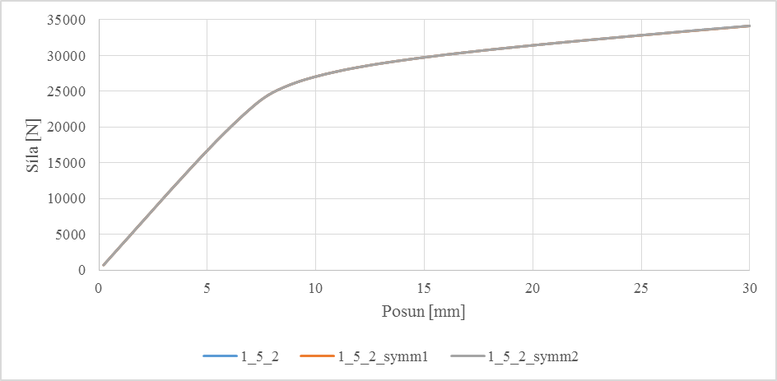
Z obr. 5. je patrné, že se křivky závislostí posunu na síle u všech tří modelů shodují, a tudíž použití symetrie prostorového modelu nemá vliv na kvalitu výsledků.
4 Závěr
Použití prvků SOLID45 hex vede se vzrůstajícím počtem elementů, na rozdíl od prvků SOLID95 hex, k přibližování k přesnému výsledku zdola. Symetrické uspořádání prvků v porovnání s nesymetrickým uspořádáním stejných prvků (SOLID95 pent) nemá významný vliv na kvalitu výsledků a rychlost konvergence výpočtu. Použití prvků SOLID92 má za následek špatnou konvergenci výpočtu. Při vyšším počtu těchto prvků výpočet konverguje, avšak výpočet je časově náročný. V porovnání konečněprvkové sítě s prvky SOLID45 hex a SOLID95 pent se ukazuje použití prvků s vnitřními stěnovými uzly jako výhodnější. Model s prvky SOLID95 pent vykazuje lepší přesnost výsledků než model s dvojnásobně menšími prvky SOLID45 hex. Výpočet je navíc přibližně dvakrát rychlejší ve prospěch sítě s prvky SOLID95 pent. Uplatnění prvků SOLID95 pent je výhodné také v porovnání s prvky SOLID95 hex. SOLID95 pent totiž zachycují výsledky ve dvou dalších uzlových bodech. Výpočty obou těchto variant jsou časově téměř stejně náročné, přestože prvků SOLID95 pent je v porovnávané síti dvakrát více než prvků SOLID95 hex a výsledky výpočtu jsou přesnější. Model s lokálním zahuštěním sítě v místě spojení dřevěných prvků a použitím prismatických prvků SOLID95 pent se jeví jako nejvýhodnější z hlediska kvality výsledků a rychlosti výpočtu. Použití symetrie vede k výraznému urychlení konvergence výpočtu.
Poděkování
Tento příspěvek vznikl v rámci projektu Univerzitní centrum energeticky efektivních budov. Výzkum byl podpořen grantem SGS14/178/OHK1/3T/11.
Literatura
- ČSN EN 338 Konstrukční dřevo – Třídy pevnosti. Český normalizační institut, Praha, 2010
- Moses D. M., Prion G. L.: Anisotropic Plasticity and Failure Prediction in Wood Composites. University Of British Columbia, Research Report, Vancouver, 2002
The aim of this article is to compare 3D numerical models of traditional timber joint. Numerical model of the subjected carpentry joint includes material nonlinearities. Material model of wood presume elasto-plastic behaviour and has orthotropic – transversal isotropic property. The finite-element meshes introduced herein differ one from other by element type and their quantity applied, type of mapping and local density of mesh. Number of nodes and elements, calculation convergence speed, FEM solution exactness, symmetry and mapping of elements are observed.