Experimentální stanovení ohybové pevnosti desek z UHPFRC
Článek je zaměřen na stanovení ohybové pevnosti tenkých desek z ultra-vysokohodnotného betonu vyztuženého ocelovými vlákny (UHPFRC). Únosnost prvků bez betonářské výztuže vyztužených pouze rozptýlenou výztuží v podobě drátků v ohybu je ovlivněna především orientací a distribucí vláken a projevuje se u nich size-effect. Speciální tělesa – deskové pruhy o různých tloušťkách 40, 50, 60, 70 a 80 mm byly testovány ve čtyřbodovém ohybu na rozpětí 1900 mm a ve tříbodovém ohybu na rozpětí 600 mm v poloze stejné jako při betonáži a obrácené dnem vzhůru. Vyhodnocené ohybové pevnosti byly porovnány s pevnostmi stanovenými referenčními ohybovými zkouškami na trámcích o velikostech 150 × 150 × 700 mm, 100 × 100 × 400 mm a 40 × 40 × 160 mm. Byly vyhodnoceny vlivy velikosti prvku, tloušťky desky, rozpětí a polohy vzhledem k betonáži na únosnost v ohybu. Experimenty byly dále podpořeny numerickou simulací.
1. Úvod
Vzhledem k tomu, že tahová odezva vláknobetonů obecně není pevně definovaná materiálová vlastnost, byly v rámci vývoje segmentů mostovky pro spřažené dřevo-UHPFRC lávky provedeny speciální ohybové zkoušky za účelem stanovení pevnosti v tahu za ohybu pro konkrétní okrajové podmínky.
2. Experimentální program
V současné době probíhá na Kloknerově ústavu ČVUT ve spolupráci s firmou NOVÁK & PARTNER, s.r.o. vývoj technologie spřažené dřevo-betonové lávky s využitím prefabrikovaných segmentů mostovky z UHPFRC. Koncepčně byly segmenty navrženy jako tenké desky konstantní tloušťky z UHPFRC vyztužené pouze rozptýlenou výztuží v podobě ocelových drátků. Segmenty jsou uloženy na dvou dřevěných trámech, se kterými jsou spřaženy. V podélném směru segmenty spolupůsobí s trámy a jsou namáhány převážně tlakovou silou a ohybem. V příčném směru staticky působí jako prostý nosník s převislými konci. Pro návrh jejich tloušťky je rozhodující únosnost v příčném směru, ve kterém jsou namáhané pozitivním i negativním ohybovým momentem a smykovou silou.
2.1 Pevnost vláknobetonů v tahu
Odezva daného materiálu na vnější silové zatížení se nazývá mechanická vlastnost a bývá charakterizována fyzikální veličinou, nejčastěji napětím (pevností) a deformací (mezní přetvoření). Tahová odezva vláknobetonů není obecně pevně definovaná materiálová vlastnost. Hodnota tahové pevnosti je závislá nejen na konkrétní receptuře, množství a vlastnostech použitých vláken a typu zkoušky, ale závisí zejména také na uspořádání a orientaci vláken v konkrétním průřezu a vyhodnocovaném směru. Uspořádání a orientace vláken jsou silně ovlivněny rozměrovým efektem (size-effect – menší tělesa vykazují vyšší pevnost) a stěnovým efektem (wall-effect – dochází k usměr-nění vláken o stěny formy, projevuje se nejvíce u tenkých prvků). Uspořádání a orientace vláken závisí kromě tvaru a velikosti konkrétního prvku také na způsobu jeho výroby. Tato problematika byla studována již mnoha autory po celém světě a je podrobně zpracována např. v (Duque et al. 2016, Kolísko et al. 2013, Zhou et al. 2013).
Uspořádání a orientace vláken (v našem případě ocelových drátků) v betonové matrici tedy není homogenní. Drátky v blízkosti bednění se orientují podélně s bedněním. Vlivem gravitace mohou drátky sedat od vrchu dolů a orientovat se spíše do vodorovné pozice. Při horním povrchu desky tak například při nevhodné konzistenci může dojít k částečné absenci drátků a naopak při spodním povrchu může dojít k jejich větší koncentraci.
U betonů běžných pevností se aplikují tři způsoby stanovení pevnosti v tahu: test příčným tahem, ohybem anebo prostým tahem. Každý test poskytuje jinou hodnotu – pevnost v prostém tahu, pevnost v tahu za ohybu (ohybová pevnost) a pevnost v příčném tahu. Pro účely materiálu UHPFRC jsou podstatné testy v ohybu či prostém tahu, ze kterých je možno odvodit přímo materiálové charakteristiky pro návrh prvků.
2.2 Zkušební tělesa pro stanovení ohybové pevnosti
Na základě různých platných norem existuje pro stanovení pevnosti betonu v tahu za ohybu více typů zkoušek, které se liší zejména velikostí vzorků a statickým schématem. Zkoušky se provádějí většinou na trámcích namáhaných čtyřbodovým či tříbodovým ohybem se zářezem či bez zářezu. O správnosti aplikace a interpretovatelnosti výsledků konkrétního zkušebního postupu pro vláknobetonové konstrukce se vedou neustále diskuse, proto bylo provedeno pro porovnání více různých typů zkoušek.
Byly provedeny zkoušky ve tříbodovém ohybu na trámcích 100 × 100 × 400 mm a 150 × 150 × 700 mm se zářezem (dle ČSN EN 14651+A1) a ve čtyřbodovém ohybu na trámcích 150 × 150 × 700 mm, 100 × 100 × 400 mm (dle ČSN P732452). Vzhledem k jemnozrnnosti UHPC byly provedeny testy také na trámcích 40 × 40 × 160 mm (pro testování cementu dle ČSN EN 196-1) ve tříbodovém ohybu bez zářezu (podle ČSN EN 12390-5). U testů ve tříbodovém ohybu se zářezem byly osazeny senzory pro měření rozevření trhliny CMOD.
Je nutno upozornit, že normové zkušební trámky mají rozpětí, které je pouze malým násobkem výšky průřezu, a proto se na jejich průhybu významnou měrou podílí smykové deformace (jejich podíl činí pro tříbod cca 18 % a pro čtyřbod cca 14 % z celkového průhybu). Současné normy nezohledňují při odvozování materiálového diagramu z naměřené závislosti síla-průhyb z ohybové zkoušky vliv smykových deformací a dochází k poměrně značným odchylkám ve výpočetní predikci průhybů, podrobněji viz (Padevěd et al. 2018).
V rámci experimentálního programu byla navržena speciální zkušební tělesa půdorysných rozměrů 2000 × 250 mm o tloušťkách 40, 50, 60, 70 a 80 mm, která byla testována ve čtyřbodovém ohybu s rozpětím podpor 1900 mm. Neporušené krajní třetiny nosníku byly po zkoušce dále testovány ve tříbodovém ohybu s rozpětím 600 mm. Polovina zkušebních těles byla zkoušena v poloze stejné jako při betonáži (normální poloha, N) a druhá polovina horním povrchem dolů (obrácená poloha, R). Schémata všech zkoušek jsou na Obr. 1.
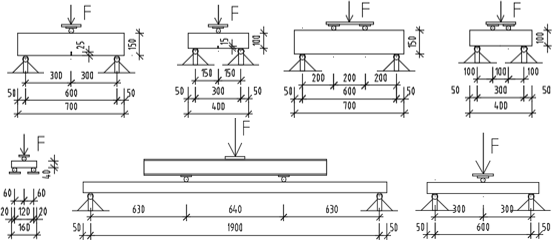
Obrázek 1: Schémata provedených zkoušek (nahoře normová tělesa, dole speciální tělesa)
2.3 Materiálové charakteristiky
| Objemová hmotnost | 2450 | kg/m3 |
| Pevnost v tlaku (krychle a = 100 mm) | 144,2 | MPa |
| Pevnost v tlaku (válec Ø150 mm) | 131,0 | MPa |
| Pevnost v tlaku (válec Ø100 mm) | 141,7 | MPa |
| Modul pružnosti | 49,6 | GPa |
Testovaná receptura UHPFRC byla složena z cementu CEM II 52,5N, jemného kameniva o velikosti do 2 mm, strusky, křemičitého úletu, vody, superplastifikátoru a ocelových drátků. Vodní součinitel byl cca 0,24. Drátky byly použity nedeformované, válcové, potažené mosazí o pevnosti 2200 MPa, délky 13 mm a průměru 0,2 mm s objemovým podílem 2 %. Základní materiálové vlastnosti stanovené experimentálně ve stáří 28 dní jsou uvedeny v Tab. 1.
3. Výsledky experimentů
Výsledky experimentů jsou záznamy závislosti síly na průhybu (viz Obr. 3–4), ze kterých je patrný materiálový diagram a ze kterých se následně vyhodnotí ohybová pevnost za předpokladu aplikace teorie lineární pružnosti. Tahová pevnost v ohybu je stanovena z maximální naměřené síly za předpokladu lineárně elastického rozdělení napětí po výšce průřezu a průřezové plochy v místě porušení. Je nutno poznamenat, že aplikace lineárně elastické teorie zakotvená v normových předpisech neodpovídá skutečnému průběhu napětí v singulárních oblastech, zejména pak v případě 3bodového ohybu se zářezem.
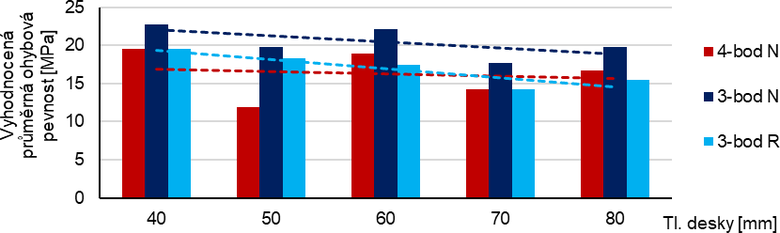
Průměrné ohybové pevnosti vyhodnocené z jednotlivých typů zkoušek jsou shrnuty v Tab. 2, kde jsou tyto hodnoty ohybové pevnosti také procentuálně porovnány vzhledem ke zkoušce ve 4bodovém ohybu na trámcích 150 × 150 × 700 mm (test č. 1), u které byla vyhodnocená pevnost nejmenší. Dále jsou u těles se stejnými rozměry průřezu stanoveny také procentuální rozdíly mezi 3- a 4bodovým ohybem.
| Test č. | Typ zkoušky | Vyhodnocená průměrná ohybová pevnost [MPa] | Porovnání s testem č. 1 | Srovnání 3bod a 4bod |
|---|---|---|---|---|
| 1 | 4bod, 150 × 150 × 700 mm | 12,5 | 100 % | 8 % |
| 2 | 3bod, 150 × 150 × 700 mm se zářezem | 13,5 | 108 % | |
| 3 | 4bod, 100 × 100 × 400 mm | 17,5 | 140 % | 9 % |
| 4 | 3bod, 100 × 100 × 400 mm se zářezem | 19,1 | 153 % | |
| 5 | 3bod, 40 × 40 × 160 mm bez zářezu | 29,9 | 239 % | – |
| 6 | 4bod, tl. 40–80 mm, rozpětí 1900 mm, normálně | 16,3 | 130 % | 25 % |
| 7 | 3bod, tl. 40–80 mm, rozpětí 600 mm, normálně | 20,4 | 164 % | |
| 8 | 3bod, tl. 40–80 mm, rozpětí 600 mm, obráceně | 17,0 | 136 % | – |
Vyhodnocené pevnosti v tahu za ohybu dosáhly v případě malých trámců 40 × 40 × 160 mm hodnoty více než dvojnásobné (2,4×) oproti trámcům 150 × 150 × 700 mm. Tento výsledek potvrzuje skutečnost, že zejména vliv stěnového efektu (usměrnění drátků) je u malých těles naprosto zásadní. Rozdíly mezi 3- a 4bodovým ohybem byly zaznamenány okolo 8–9% u normových těles, u speciálních těles s výrazně větším rozpětím dosahovaly až k cca 25 %. Rozdíly mezi 3- a 4bodovým ohybem jsou dány zejména skutečností, že v případě 3bodového ohybu je místo porušení pevně definováno, zatímco u 4bodového ohybu dochází k porušení v nejslabším místě ve vnitřní třetině rozpětí nosníku. Únosnost desek v obrácené poloze byla průměrně o cca 20 % nižší oproti normální poloze, ve které byly desky betonovány. Tento rozdíl byl dán nerovnoměrným rozdělením drátků po výšce průřezu způsobeným vlivem gravitace a méně vhodnou konzistencí.
V diagramu na Obr. 2 jsou vyhodnocené průměrné hodnoty ohybové pevnosti speciálních těles pro jednotlivé tloušťky desek 40–80 mm. Červené sloupce znázorňují výsledky ze 4bodového ohybu, modré sloupce výsledky ze 3bodového ohybu pro tělesa v normální (N) a obrácené poloze (R). Čárkovanou čarou je vyznačen trend klesající pevnosti s rostoucí tloušťkou desky.
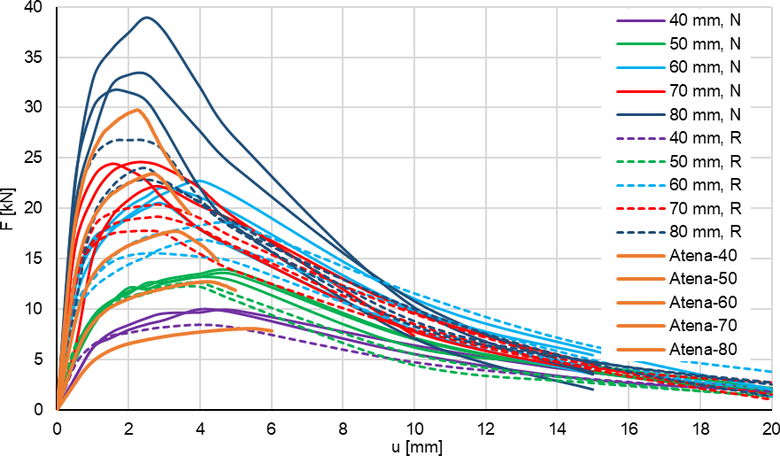
Obrázek 3: Záznamy zkoušek deskových pruhů tl. 40–80 mm ve 3bodovém ohybu, doplněno numerickou simulací v programu ATENA (stejné materiálové parametry, různé tloušťky desek)
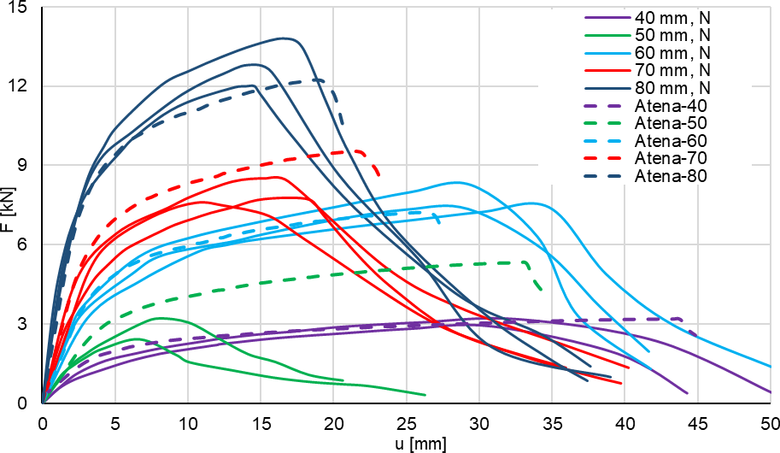
Obrázek 4: Záznamy zkoušek deskových pruhů tl. 40–80 mm ve 4bodovém ohybu, doplněno numerickou simulací v programu ATENA (stejný materiál, různé tloušťky desek)
Ze zkušeností s aplikací UHPFRC vyplývá, že tenčí desky se chovají výrazně duktilněji než desky tlustší. Ze záznamů zkoušek ve čtyřbodovém ohybu na Obr. 4 je toto chování dobře patrné u desek tloušťky 40, 60 a 80 mm, kdy pro desky tl. 40 mm je porušení dosaženo při cca dvojnásobném průhybu oproti deskám tl. 80 mm. Zkušební tělesa tl. 50 mm ve čtyřbodovém ohybu zcela vybočují z důvodu lokálních poruch v distribuci drátků, u tříbodového ohybu lze pozorovat pouze lehce sníženou únosnost v normální poloze. Desky tl. 70 mm vykazují nižší pevnost a duktilitu oproti očekávání ve všech případech.
4. Numerická simulace
V programu ATENA byly namodelovány zkoušky ve 3- a 4bodovém ohybu pro vyšetřované tloušťky desek 40–80 mm. Pro simulaci materiálu UHPFRC byl aplikován jeden materiálový model Nonlinear cementitious 2 pro celý průřez. Pro daný typ zkoušky byly použity vždy stejné materiálové parametry pro všechny tloušťky desek, aby byly lépe patrné odchylky dané rozdílnou distribucí vláken pro různé tloušťky desek. Výsledné zatěžovací křivky jsou zaneseny do grafů na Obr. 3 a 4.
Numerickou simulací v programu ATENA lze dosáhnout velmi dobré shody s experimenty, ovšem při aproximaci průřezu prvků z UHPFRC homogenním materiálem nelze materiálový model zcela univerzálně aplikovat pro různé okrajové podmínky a je nutno jej kalibrovat pro konkrétní případy dané velikostí, tvarem a způsobem odlévání prvku do formy. Určitým řešením pro možnost částečně univerzální aplikace by mohl být vrstvičkový model, který by zohledňoval rozdílnou distribuci drátků po výšce průřezu. Tento model je složen z více vrstev o různých materiálových parametrech a v současnosti se zabýváme jeho laděním.
5. Závěr
Vyhodnocená ohybová pevnost (pevnost v tahu za ohybu) UHPFRC se významně liší v závislosti na velikosti zkušebního tělesa a typu zkoušky. Trámce 40 × 40 × 160 mm vykazovaly až 2,4× větší ohybovou pevnost než trámce 150 × 150 × 700 mm. Tento výsledek potvrzuje skutečnost, že vliv zejména stěnového efektu (usměrnění drátků) na mechanické vlastnosti je u malých těles naprosto zásadní. Dále byl pozorován určitý trend rostoucí duktility a ohybové pevnosti se snižující se tloušťkou desky. Z testů ve 4bodovém ohybu byla vyhodnocena nižší ohybová pevnost oproti testům ve 3bodovém ohybu. Rozdíly mezi 3- a 4bodovým ohybem byly zaznamenány okolo 8–9 % u normových těles, u speciálních těles s výrazně větším rozpětím dosahovaly až k cca 25 %. Rozdíly mezi 3- a 4bodovým ohybem jsou dány zejména skutečností, že v případě 3bodového ohybu je místo porušení pevně definováno, zatímco u 4bodového ohybu dochází k porušení v nejslabším místě ve vnitřní třetině rozpětí nosníku. Ohybová pevnost u deskových těles betonovaných ve vodorovné poloze byla cca o 20 % nižší při zatěžování v obrácené pozici. Tento rozdíl byl dán nerovnoměrným rozdělením drátků po výšce průřezu vlivem gravitace. Numerickou simulací v programu ATENA lze dosáhnout velmi dobré shody s experimenty, ovšem při aproximaci průřezu prvků z UHPFRC homogenním materiálem nelze materiálový model zcela univerzálně aplikovat pro různé okrajové podmínky a je nutno jej kalibrovat pro konkrétní případy. Na závěr je nutno upozornit, že aplikace lineárně elastické teorie zakotvená v normových předpisech pro stanovení ohybové únosnosti neodpovídá skutečnému průběhu napětí v singulárních oblastech a dále, že tyto normy nezohledňují při odvozování materiálového diagramu z naměřené závislosti síla-průhyb z ohybové zkoušky vliv smykových deformací, podrobněji viz (Padevěd et al. 2018).
Poděkování
Experimenty byly provedeny s podporou TAČR v rámci projektu TH02020730 – Využití UHPC pro moderní návrh progresivních spřažených dřevo-betonových mostních konstrukcí.
Literatura
- AFGC (2013) Ultra high performance fibre-reinforced concrete: Interim Recommendations, Revised edition, AFGC publication, France
- Červenka V., Červenka J., Pukl R. (2002) ATENA – A tool for engineering analysis of fracture in concrete, Sadhana 27/4.
- ČSN EN 14651+A1, Test method for metallic fibered concrete – Measuring the flexural tensile stregth (limit of proportionality, residual), 11/2008
- ČSN EN 196-1, Methods of testing cement – Part 1: Determination of strength, 10/2016
- ČSN EN 12390-5, Testing hardened concrete – Part 5: Flexural strength of test specimens, 10/2009
- ČSN P732452, Fibre-reinforced concrete – Testing of hardened fibre-reinforced concrete, 06/2015
- Duque, L.F.M., Varga, I. and Graybeal, B.A. (2016) Fibre Reinforcement Influence on the Tensile Response of UHPFRC, In First International Interactive Symposium on UHPC – 2016, Des Moines, IOWA, USA
- Holý, M., Čítek, D., Tej, P., Vráblík, L. (2018), Ohybová pevnost tenkých desek z UHPFRC, 25. Betonářské dny (2018) Sborník příspěvků konference, ISBN 978-80-906759-6-4
- Holý, M., Čítek, D., Tej, P., Vráblík, L. (2018), Material Properties of Thin UHPC Slabs Used for Timber-Concrete Composite Bridge, The 10th International Conference on Short and Medium Span Bridges (SMSB 2018), Quebec Canada
- Kolísko, J., Rydval, M. and Huňka, P. (2013) UHPC – Assessment of Steel Fibre Distribution and Matrix Homogeneity. In fib Symposium TEL-AVIV 2013 Engineering a Concrete Future: Technology, Modeling & Construction – Proceedings. IACIE, Tel Aviv, Israel, p. 113–116
- Metodika 1 – Metodika pro návrh UHPC a pro materiálové zkoušky (2015), výstup projektu TAČR TA01010269, Kloknerův ústav ČVUT v Praze, 2015
- Padevěd P., Křístek, V., Strobach, C. P. (2018), Efekt smykových deformací při ohybových zkouškách kvazikřehkých materiálů, 25. Betonářské dny (2018) Sborník příspěvků konference, ISBN 978-80-906759-6-4
- Zhou, B., Uchida, Y. (2013), Fiber orientation in ultra high performance fiber reinforced concrete and its visualization, Proceedings of 8th International conference on Fracture Mechanics of concrete and Concrete StructuresFraMCos-8, Toledo, Spain
Článek se zabývá problematikou stanovování ohybových pevností z ultravysokopevnostních betonů vyztužených ocelovou rozptýlenou výztuží pro výrobu tenkostěnných desek pro využívání ve spřažených dřevěných a UHPC konstrukcí. Tento typ technologie je zatím využíván v praxi velmi málo, zkušenosti s jeho aplikací jsou tudíž minimální, přičemž se jedná o technologii budoucnosti. Autoři pro ověření mechanických vlastností použili zkušební tělesa odlišných rozměrů, na kterých aplikovali několik zatěžovacích schémat. Potvrdil se výrazný vliv rozměrů těles i způsobů zatížení na výsledné hodnoty ohybových pevností. Současně byla provedena numerická simulace v programu Atena. Porovnání výsledků prokázalo nutnost kalibrovat výpočetní modely pro tyto typy zkoušek materiálu UHPFRC.
Článek přispívá k propagaci tohoto moderního materiálu a ukazuje na reálné využití v praxi. Doporučuji ho proto k publikování na TZB-info.
This paper focuses on the determination of the flexural strength of thin slabs made of the Ultra High Performance Fiber Reinforced Concrete (UHPFRC). The load-bearing capacity in bending of elements reinforced only with steel fibers (used as a scattered reinforcement) is primarily influenced by the orientation and distribution of the fibers. A size-effect occurs by these elements. The bending tests were executed on some special test specimens – slabs strips. The slab strips of various thickness of 40, 50, 60, 70 and 80 mm were tested in 4-point bending tests with span 1900 mm and in 3-point bending tests with span 600 mm. Half of the test specimens was tested in casting position, the other half was tested upside down. The obtained values of the flexural strength were compared to values from reference bending tests of the beams 150 × 150 × 700 mm, 100 × 100 × 400 mm and 40 × 40 × 160 mm. An influence of the different size of the tested specimen, of the slab thickness, of the span size and of the positioning of the slab with respect to the direction of casting on the flexural strength are evaluated. The experiments were further supported by numerical simulation.