Numerická analýza chování dřevobetonové konstrukce
Předmětem této práce je numerická analýza chování dřevobetonové kompozitní stropní konstrukce, tvořené betonovou deskou a dřevěnými nosníky z lepeného lamelového dřeva. Hlavním cílem je posoudit možnost využití betonové desky, která spolupůsobí s dřevěnými trámy a pomocí modelů v programu ANSYS vyšetřit její chování v zatížené stropní konstrukci. Přesnost numerické analýzy dřevobetonových konstrukcí plně závisí na použitých materiálových modelech, proto budou provedené materiálové modely později ověřeny na základě experimentálních výsledků.
1. Úvod
Na celém světě je prosazována myšlenka využití dřeva jako stavebního materiálu z důvodu zachování přírodních zdrojů a životního prostředí. Se vzrůstajícími nároky na únosnost a rozpětí konstrukcí jsou ale nutná nová řešení dřevěných konstrukcí, mezi která patří použití vrstveného dřeva, lepeného lamelového dřeva nebo spojování dřeva s dalšími materiály v kompozitní konstrukce, kde spolupůsobí s betonem, ocelí nebo s jinými vysokopevnostními materiály. Efektivní kombinací dřeva a dalších materiálů se předpokládá rozšíření možností stavebních konstrukcí vzhledem k aktivaci spolupůsobení a tím využití výborných vlastností všech materiálů při posuzování konstrukční a požární odolnosti. Takové konstrukce pak odolávají mnohem větším zatížením na větší rozpětí a umožňují tak postavit moderní dřevěné stavby mnohem vyšší a větší, než bylo možné před 50 lety.
V současné době se ve světě i u nás velmi uplatňuje spojení dřeva a betonu. Možnost využití kompozitní dřevobetonové konstrukce v pozemním stavitelství lze uvažovat při zesilování a rekonstrukci historických staveb s dřevěnými stropními nosníky nebo deskami a při realizaci nových vícepodlažních dřevostaveb. Současné evropské i světové normy však dostatečně nepokrývají problematiku možnosti spřažení těchto dvou kompozitů. Navrhování těchto spojů probíhá čistě empirickou metodou, je velmi konzervativní a nevystihuje skutečné chování konstrukce (otlačení dřevěného trámu, otlačení desky, prokluz spřahovacího trnu atd.). Spoje jsou tak velmi významně předimenzovány.
Analýza skutečného chování konstrukčního prvku nebo konstrukčního systému může být provedena buď pomocí experimentů, nebo za použití numerického modelování. Mnohdy nákladné experimenty mohou z části nahradit numerické modely, avšak nutnou podmínkou je zavedení přesných materiálových modelů, které s dostatečnou přesností aproximují reálné vlastnosti a dále zavedení jen nejnutnějších zjednodušujících předpokladů, které nebudou mít vliv na výsledky numerických simulací a jejich shodu s reálným chováním konstrukce. Vždy je však třeba verifikovat výsledky numerické analýzy s experimentem, nebo naopak kalibrovat parametry numerického modelu podle provedených experimentů. Numerické modely tak lze výhodně využít k pravděpodobnostním a spolehlivostním analýzám a optimalizačním studiím, které umožní nejefektivnější využití výhodných fyzikálních vlastností při současném zachování požadavků spolehlivosti na konstrukci [1].
2. Cíle modelování
Při vytváření numerického modelu kompozitních konstrukcí musí být uvažovány čtyři hlavní faktory, kterými jsou materiálové vlastnosti, geometrické vlastnosti, vnitřní a vnější spolupůsobení mezi jednotlivými prvky a uspořádání sestavy zkoušky, použité při experimentu. Materiálové vlastnosti se skládají z mechanických vlastností (elastické a plastické vlastnosti), rozvrstvení a drcení. Geometrické vlastnosti zahrnují rozměry vzorků, imperfekce ve vzorcích, druhy spojovacích prostředků a zda je spojovací prostředek s předvrtáním nebo bez předvrtání. Vnitřním spolupůsobením se rozumí kontakt mezi dřevem, betonem a spojovacím prostředkem, které může být spojováno se třením. Nakonec je důležitý vliv uspořádání zkoušky, protože různé zkoušky a různá uspořádání způsobují různý přenos napětí, a tudíž rozdílné deformace. Tento problém nemusí být přítomen v kompozitních konstrukcích, avšak je přítomen ve zkouškách jednotlivých spřahovacích prostředků, proto musí být také zohledněn [2].
V tomto modelu byly za nejdůležitější faktory uvažovány materiálové vlastnosti, uvažující elasticitu, plasticitu a zpevnění, drcení betonu, spolupůsobení mezi materiály, uvažující kontakt se třením a geometrické nelinearity, způsobené velkými deformacemi ve zkoušeném vzorku.
Správné fungování modelu je ovlivňováno správným zavedením materiálu (dřevo, beton, spřahovací prostředky) a spolupůsobením jednotlivých makroprvků modelu (dřevěný trám, betonová deska, spřahovací prostředky). Na základě správnosti těchto faktorů budou později výsledkem pracovní diagramy použitých materiálů, jejich porovnání se skutečně provedenými zkouškami a konečný pracovní diagram stropní konstrukce pro danou tloušťku betonové desky.
3. Materiálové vlastnosti modelu
3.1. Dřevo
Materiálový model dřeva je zvolen jako lineárně elastický, s materiálovými parametry odpovídající třídě GL24h, což bylo v počáteční fázi numerických simulací přijatelné zjednodušení. Materiálový model dřevěného komponentu byl idealizován bilineárním pracovním diagramem s nulovým zpevněním po vyčerpání únosnosti.
Do modelu byly zahrnuty parametry v Tab. 3.1. Bilineární pracovní diagram pro dřevěné trámy je experimentálně zjištěn a zaveden do modelu. Při experimentálním zjišťování pevnostních charakteristiky jsou zjištěny 4 oblasti:
- počáteční vyrovnávání testovacího vzorku
- lineárně elastická oblast
- oblast plastických deformací
- oblast po porušení testovacího vzorku
| Charakteristika | GL24h |
| Pevnost v ohybu [MPa] | 24 |
| Poissonovo číslo | 0,3 |
| Průměrná hodnota modulu pružnosti [MPa] | 11600 |
| Modul zpevnění [MPa] | 0 |
3.2. Kontakt
Spojení je v úvodních srovnávacích numerických analýzách vytvořeno jako dokonale tuhé. V dalším výzkumu bude zaveden nelineární model spojitého spřažení, jehož parametry budou získány na základě provedených experimentů protlačovacích zkoušek a současně bude probíhat tvorba numerického modelu s diskrétním modelováním spřahovacích prvků. Na závěr bude provedeno porovnání diskrétního způsobu modelování se spojitým na základě výsledků protlačovacích zkoušek.
Popis spojitého modelování spřažení
Jedná se o modelování spřažení pomocí tzv. přechodové vrstvy mezi dřevěným trámem a betonovou deskou. Tato přechodová vrstva je určena jednotlivými materiálovými parametry, které musí odpovídat charakteristikám zjištěných experimentem (protlačovací zkouškou). Ty závisí na typu stahovacího prostředku a jeho materiálových vlastnostech, počtu prvků v jakém se na trámu nachází, sklonu prvků vůči ose trámu a také na materiálových vlastnostech dřeva a betonu.
Výhodou použití tohoto modelování je, že tento model není příliš náročný na výpočet a není příliš náchylný k chybám. Parametry materiálového modelu spřahovací vrstvy tak mohou být upravovány, aby se výsledky numerické analýzy protlačovací zkoušky co nejvýstižněji blížily k jejím experimentálně zjištěným hodnotám. Takto verifikovaný materiálový model lze aplikovat v celkovém modelu dřevobetonové kompozitní konstrukce a jeho výsledky výstižně aproximují chování reálné konstrukce [3].
Popis diskrétního modelování spřažení
Jedná se o modelování spřažení, kdy jsou jednotlivé spřahovací prvky modelovány diskrétně objemovými konečnými prvky jako geometrické entity s uvážením hloubky zapuštění do dřevěného trámu a betonové desky.
Nevýhodou tohoto způsobu modelování je velká časová náročnost při tvorbě modelu (volba materiálu pro spřahovací trn, vlastnosti kontaktů trnu se dřevem či betonem) a především mimořádné nároky na výpočetní techniku, zvláště pokud jsou materiálové modely jednotlivých komponentů fyzikálně nelineární. Na druhou stranu je výhodou získání velmi přesných informací o deformaci trnu v průběhu zatěžovací zkoušky a vývoj napětí a přetvoření v okolí trnu. Tyto hlediska jsou určující pro citlivý návrh spřahovacích prvků v případech, kdy otlačení spřahovacího trnu v dřevěném trámu i betonové desce hraje nezanedbatelnou roli v celkovém chování spřažení [3].
U obou metod bude stěžejním problémem identifikace jednotlivých parametrů materiálových modelů kontaktů. Tento proces je většinou iterační, protože parametry implementovaných materiálových modelů často neposkytují uspokojivé výsledky, i když jsou odvozeny z výsledků experimentu. Jako první krok v iteračním procesu byl proto, pro účely přípravy vstupů do programu ANSYS, proveden výpočet charakteristických únosností spřahovacích prostředků podle DIN:
- Charakteristická únosnost jednoho šroubu v tahu Rk,T = 13 kN
- Charakteristická únosnost šroubu na ohyb Rk,M = 15 Nm
- Smykový modul pružnosti jednoho šroubu pod úhlem 45° Kser = 1066 N/mm
- Návrhová únosnost jednoho šroubu ve smyku Td = 3,73 kN
Výpočet zohlednil kvalitu a rozměry dřeva, tloušťku betonové desky, průměr šroubu, sklon šroubu a efektivní délku šroubu. Únosnost spřahovacích prvků je navýšena o 20 %, což je provedeno na základě Koželouhových zkoušek protlačení, které prokázaly nárůst únosnosti vlivem prokluzu a otlačení spřahovacích prostředků vůči normě. Tato únosnost, vyjádřená v N, bude vydělena styčnou plochou dřevěného trámu a drátkobetonové desky, vyjádřenou v mm2. Získáme tak únosnost spáry ve střihu.
3.3. Beton
Materiálový model betonové desky byl v prvním kroku volen jako lineárně elastický, s materiálovými parametry podle tabulky Tab. 3.2. V další fázi postupného zavádění nelinearit bude aplikován nelineární materiálový model betonu, získaný z dalších zkoušek, tedy zkoušek v tlaku a v příčném tahu krychlí o hraně 150 mm a trámů 4bodovým ohybem v Ústavu teoretické a aplikované mechaniky v září tohoto roku.
| Charakteristika | FRC |
| Pevnost v tlaku [MPa] | 45 |
| Pevnost v tahu za ohybu [MPa] | 3,8 |
| Ekvivalentní pevnost v tahu [MPa] | 1,6 |
| E-modul [MPa] | 36000 |
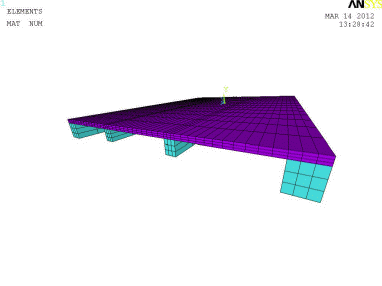
Obr. 4.1: Numerický model kompozitní dřevobetonové desky
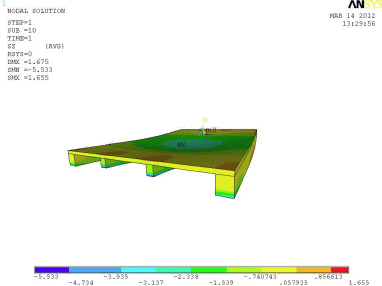
Obr. 4.2: Výsledky numerického modelu výpočtu MKP, normálové napětí
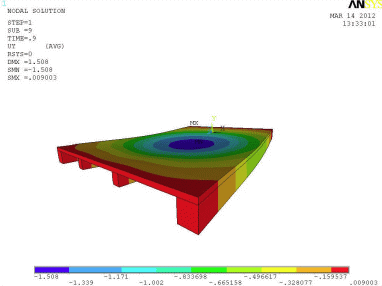
Obr. 4.3: Výsledky numerického modelu výpočtu MKP, průhyb
Pracovní diagram betonu v tahu je možné získat přímo zkouškou v příčném tahu. Ta však předpokládá zcela homogenní chování materiálu v celém průřezu, což v případě betonu nebo vláknobetonu nelze zcela zaručit. Proto se vedle zkoušky osovým tahem provede rovněž zkouška v tahu za ohybu, jejímž výsledkem bude vztah mezi působící silou a deformací (průhybem), nikoliv přímo konstitutivní vztah mezi přetvořením ε a napětím σ.
V průběhu zkoušky v tahu za ohybu lze chování rozdělit na oblast, ve které se nosník chová přibližně lineárně až po dosažení takového průhybu, při kterém se vytvoří první trhlina a na oblast charakterizovanou deformačním změkčením, tedy poklesem zatěžovací síly s rostoucím průhybem.
4. Popis modelu
Prostorový model byl vytvořen následujícím způsobem. Nejprve byly definovány systémové body, které byly následně spojeny liniemi, ze kterých se vytvořily plochy. Z ploch následně vznikly objemové prvky, kterým byly přiřazeny materiálové vlastnosti. V modelu byly použity dva konečné prvky: SOLID45, SOLID65.
Prvek SOLID45 byl použit pro dřevo a prvek SOLID65 pro beton. Zdrojový soubor byl zhotoven tak, aby umožňoval změnu všech parametrů, kterými je definována geometrie a materiálové vlastnosti modelu. Je tak možné např. měnit tloušťku betonové vrstvy a průřez dřevěného prvku a pomocí experimentů bude možné provést studii přiléhavosti materiálového modelu s vlivem různých parametrů.
Jedná se o po obvodě podepřenou desku. Zatížení bylo aplikováno plošně na horní betonovou desku (obr. 4.1). Výsledný průběh napětí od návrhového zatížení fd = 4 kN/m je na obr. 4.2, průhyb nosníku na obr. 4.3.
5. Závěr
K rozšíření zkoušky chování dřevobetonových konstrukcí byl pro tvorbu nelineárních numerických modelů využit program ANSYS 11. Numerický model se skládá z mechanické analýzy konstrukce. Parametry materiálových modelů spřažení budou odvozeny na základě chystaných protlačovacích zkoušek, provedených v laboratořích Fakulty stavební, ČVUT a Ústavu teoretické a aplikované mechaniky. Verifikace parametrů materiálových modelů spřažení, odvozených z chystaných zkoušek, bude provedena nelineární numerickou simulací experimentů. Podmínkou pro výstižnou numerickou simulaci bude zavedení reálného materiálového modelu, tedy vztahu mezi přetvořením ε a napětím σ [4].
Poděkování
Tento příspěvek byl zpracován za podpory projektu SGS11/109/OHK1/2T/11.
Literatura
- [1] Dias, A.M.P.G., Van de Kuilen, J.W., Lopes, S., Cruz, H. A non-linear 3D FEM model to simulate timber-concrete joints. Advances in Engineering Software 38 (2007).
- [2] Kuklíková, A.: Kompozitní dřevobetonové konstrukce, ČVUT v Praze, Fakulta stavební, 2004.
- [3] Petřík, V., Philipp, N., Křístek, V., Půlpán, M. Full-scale testy kompozitních konstrukcí FRC-dřevo a UHPFRC-dřevo. 18. konference Betonářské dny, Sekce: Mosty 2, str. 337–342, 2011.
- [4] Petřík, V., Broukalová, I. Some aspect of nonlinear analysis of timber-fibre concrete composite. Fibre Concrete 2011. Prague 2011.
- [5] Šlapka, P. Numerická simulace chování spřažených dřevovláknobetonových konstrukčních prvků. ČVUT v Praze, Diplomová práce, 2011.
The object of this work is a numerical analysis of the behavior of wood-concrete composite ceiling structure, consisting of concrete slab and wooden beams of glued laminated timber. The main objective is to explore the use of concrete slabs, which assists with wooden beams, and using models in ANSYS to investigate its behavior in the load floor construction. The accuracy of numerical analysis of wood-concrete structure fully depends on the material models. Therefore the material models will be later verified by experimental results.