Analýza prútovej škrupinovej konštrukcie z dreva
Príspevok pojednáva o teoretickej tvarovej a stabilitnej analýze drevenej prútovej škrupinovej konštrukcie. Osobitosť prístupu pri analyzovaní konštrukcie tohto typu sa vzhľadom na komplikovaný tvar strešnej roviny prejavuje vo viacerých častiach návrhového postupu. Tieto špecifiká možno vztiahnúť už na prvotnú fázu vytvárania tvaru konštrukcie, s čím priamo súvisí výsledná statická efektívnosť konečného návrhu. Ďalšími dôležitými časťami analýzy konštrukcie, ktoré vybočujú z normou definovaných postupov je stanovenie návrhového zaťaženia vonkajšími klimatickými vplyvmi a stabilitná analýza s potrebou aplikácie geometricky nelineárneho výpočtu s vplyvom počiatočných imperfekcii.
1. Úvod
Drevo ako stavebný materiál ponúka čoraz viac možnosti vytvárať tvarovo zaujímavé a staticky efektívne konštrukcie. Uplatnenie drevených prútových škrupinových konštrukcii v stavebnom priemysle teda nemá význam len z hľadiska funkcie daného objektu, ale vynikajú tiež schopnosťou sledovať modernú architektúru a esteticky sa začleniť do okolitého prostredia.
2. Opis analyzovanej konštrukcie
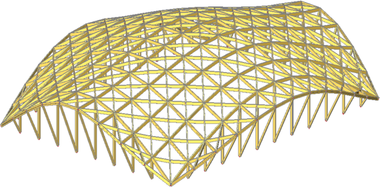
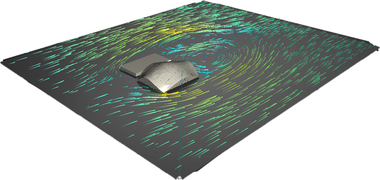
Konštrukcia, ktorá bola analyzovaná (Obr. 1) je namodelovaná z lepeného lamelového dreva pevnostnej triedy GL28h. V strešnej rovine ide o sústavu ortogonálnych zakrivených nosníkov prierezu 150/500, doplnených diagonálnym systémom drevených prvkov rovnakého prierezu.
Obr. 1: Axonometria výpočtového modelu
Ortogonálny systém nosníkov je ukladaný na sústavu hlavných oblúkov. Hlavné oblúky prierezu 200/500 sa spolu s diagonálnym systémom stretávajú v rohoch objektu v spoločných bodoch podopretia. Rozpätie hlavných oblúkov je definované pôdorysnými rozmermi konštrukcie 48 m a 36 m. Vzopätie týchto oblúkov je 10 m. Konštrukcia je vo všetkých 4 smeroch vykonzolovaná a podopretá systémom sklonených stĺpikov. Vzdialenosti priečnych väzieb sú 4 m. Najvyšší bod konštrukcie sa nachádza vo výške 15,5 m nad úrovňou terénu.
3. Vytvorenie analytického modelu
Výpočtový model bol vyhotovený v programe SCIA Engineer. Pre vytvorenie prútového modelu viackrát zakrivenej strešnej roviny bola zvolená metóda deformovania rovinnej prútovej siete.
Na výsledný tvar deformovanej siete majú vplyv tri základné faktory:
- okrajové podmienky,
- veľkosť a poloha zaťaženia,
- mierka vykreslenia priestorovej deformácie.
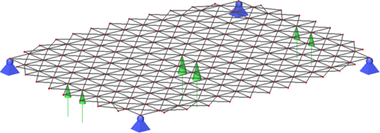
V prvom kroku bola vytvorená sieť ortogonálnych prútov v rastri 4 mx × 4 m doplnená o diagonálne prvky. V rohoch siete boli definované okrajové podmienky kĺbového podopretia a následne bola prútová sieť zaťažená osamelými silami v troch dvojiciach rozhodujúcich uzlov, s najväčšou hodnotou zaťaženia v strede (Obr. 2a).
a)
b)
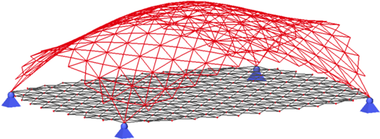
Obr. 2: Tvorba výpočtového modelu – a) Rovinná prútová sieť pred deformáciou, b) Deformovaný tvar siete
Získaný deformovaný tvar (Obr. 2b) pôvodne rovinnej sústavy prútov bol následne prevzatý vo forme čiar, ktoré popisovali výsledný tvar konštrukcie.
4. Zaťaženie klimatickými vplyvmi
Obr. 3: Usporiadanie závejového zaťaženia snehom na strešnú konštrukciu
Osobitosť návrhu škrupinovej konštrukcie sa prejavila najmä pri stanovení zaťažení klimatickými vplyvmi, nakoľko tvar a geometria strešnej roviny je normovými spôsobmi ťažko popísateľná.
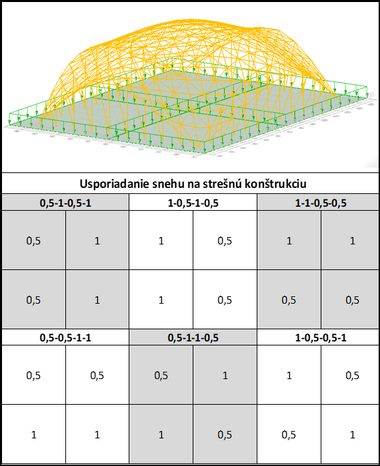
Zaťaženie snehom na konštrukcii prislúchalo s ohľadom na uvažovanú zemepisnú polohu ako bežnej, tak mimoriadnej situácii. Okrem konštantnej hodnoty zaťaženia snehom na celý pôdorysný priemet sa uvažovalo aj s nesymetrickým usporiadaním zaťaženia, pričom využitá bola symetria konštrukcie cez štvrtinovú veľkosť pôdorysnej plochy (Obr. 3).
Pre stanovenie zaťaženia vetrom bol zvolený program Flow Design (Obr. 4), ktorý umožňuje prostredníctvom modelu konštrukcie vytvoriť podmienky pre stanovenie vonkajšieho tlaku na jednotlivých oblastiach pomocou veterného tunelu.
Obr. 4: Model obtekania konštrukcie vetrom vo veternom tuneli
Obr. 5: Smer pôsobenia vetra 0° – výsledné hodnoty tlaku vetra na príslušné plochy strešnej roviny
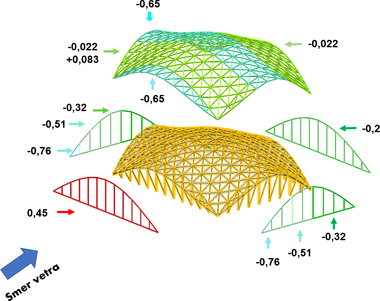
Na základe získaných hodnôt vo forme farieb, kontúr a extrémov namáhania, bolo možné výsledky zaťaženia interpretovať na reprezentatívnych oblastiach konštrukcie vo výpočtovom modeli pre všetky štyri smery pôsobenia vetra (Obr. 5).
5. Lineárna analýza konštrukcie
Lineárna analýza poslúžia pre prvotnú optimalizáciu prierezov z hľadiska tuhosti, napätia a deformácii konštrukcie. Pre podrobnú analýzu a výsledné posúdia jednotlivých prvkov bolo kľúčové vykonať globálnu stabilitnú analýzu a následne spustiť geometricky nelineárny výpočet.
6. Globálna stabilitná analýza
Vzhľadom na typ riešenej konštrukcie nie je možné objekt posúdiť bežnými postupmi z prostredia lineárnej analýzy.
Pre stabilitnú analýzu sa zvolili 4 kombinácie zaťaženia, od ktorých sa následne odvíjali tvary straty stability zohľadnené v geometricky nelineárnom výpočte. Zohľadnené boli nasledovné návrhové kombinácie:
- Kombinácia A: [G0+G1]1,35+1,5Q1
Q1 – konštantné zaťaženie snehom - Kombinácia B: [G0+G1]1,35+1,5W2
W2 – vietor – smer 0° (Obr. 6) - Kombinácia C: [G0+G1]1,35+1,5Q2
Q2 – sneh, typ – 1-0,5-1-0,5 (Obr. 4) - Kombinácia D: [G0+G1]1,35+1,5Q3
Q3 – sneh, typ – 1-1-0,5-0,5 (Obr. 4)
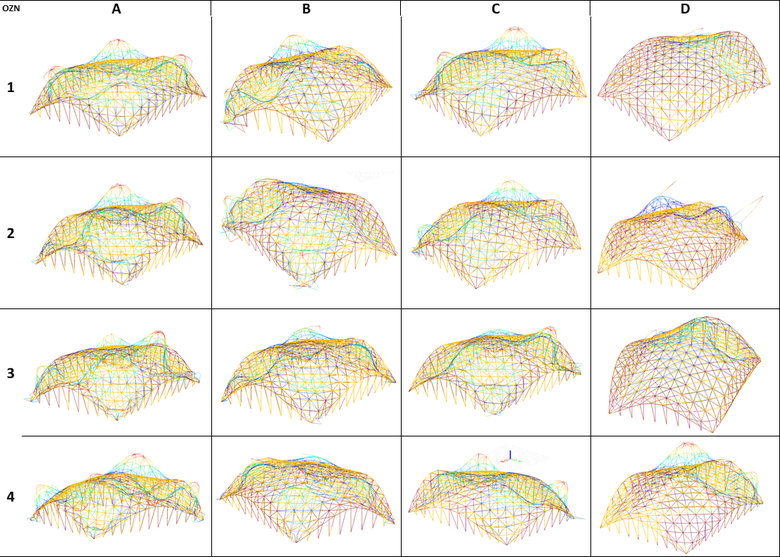
Z každej z uvedených kombinácii boli zo stabilitného výpočtu zvolené prvé štyri tvary straty stability s prislúchajúcim súčiniteľom rozdvojenia rovnováhy. Každý uvedený tvar vybočenia sa vzťahuje na celú konštrukciu. Celkovo bolo definovaných 16 tvarov straty stability konštrukcie (Obr. 6), ktoré sa uvážili v ďalšom výpočte ako možné počiatočné imperfektné tvary.
Obr. 6: Globálne tvary straty stability
7. Stanovenie počiatočnej imperfekcie
Veľkosť počiatočnej imperfekcie bola stanovená v zmysle [7] pre nesymetrické zaťaženie. Nakoľko však konštrukcia nezodpovedá normou definovanému oblúku pre stanovenie veľkosti počiatočnej imperfekcie, uvažuje sa vo výpočte kvôli bezpečnosti návrhu aj s dvojnásobnou hodnotou. Pre geometricky nelineárny výpočet boli uvážené nasledovné hodnoty počiatočných imperfekcii:
- e0 = 90 mm
- 2 × e0 = 180 mm.
8. Geometricky nelineárny výpočet
Veľkosti počiatočných imperfekcii môžu pre príslušné tvary straty stability nadobúdať kladnú aj zápornú hodnotu, pôvodnej aj dvojnásobnej veľkosti. Vstupné parametre, ktorými sú tvary vybočenia a hodnoty počiatočných imperfekcii boli prisúdené štyrom zvoleným kombináciám pre geometricky nelineárny výpočet. Zohľadnené boli tieto návrhové kombinácie:
- NC1: [G0+G1]1,35+1,5Q1
Q1 – konštantné zaťaženie snehom - NC2: [G0+G1]1,35+1,5W2
W2 – vietor – smer 0° (Obr. 6) - NC3: [G0+G1]1,35+1,5Q1+0,9W2
- NC4: [G0+G1]1,35+1,5Q4
Q4 – sneh, typ – 0,5-1-1-0,5 (Obr. 4)
Celkovo bolo vyhodnotených 256 nelineárnych kombinácii, ktoré boli rozdelené do ôsmich obálok.
9. Vyhodnotenie geometricky nelineárneho výpočtu
Obr. 7: Grafické vyhodnotenie extrémov vnútorných síl – Hlavné oblúky: N, M, V
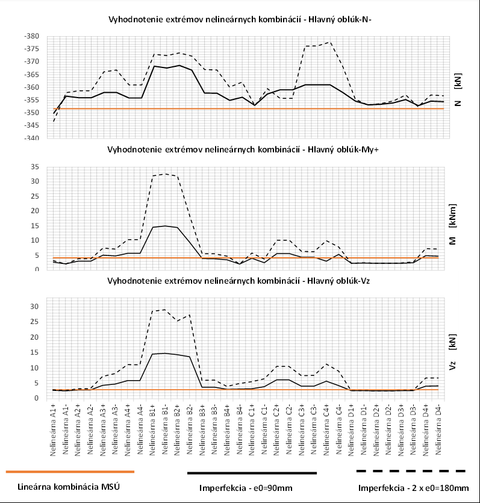
Analýza a vyhodnotenie boli vztiahnuté na výslednú napätosť základných prvkov konštrukcie. Napätosť je vyhodnotená na základe extrémov z ôsmich nelineárnych obálok, z ktorých každá obsahuje 32 kombinácií zaťaženia pre príslušné tvary straty stability a veľkosti počiatočných imperfekcií. Vzperné dĺžky a súčinitele vzperu v lineárnej analýze pre izolované prúty neboli zisťované, nakoľko priestorové spolupôsobenie jednotlivých prvkov najlepšie vystihuje globálna analýza konštrukcie. Grafické vyjadrenie prírastkov (Obr. 7) reprezentuje vplyv tvarov vybočenia a počiatočnej imperfekcie s kladnou aj zápornou hodnotou na vnútorné sily. Na zvislej osi je vyznačená veľkosť vnútornej sily. Na vodorovnej osi sa nachádza označenie konkrétneho tvaru vybočenia, pričom znamienko značí, či ide o kladnú alebo zápornú hodnotu počiatočnej imperfekcie. Oranžovou farbou je pre porovnanie vyznačená pôvodná veľkosť vnútornej sily získaná lineárnym výpočtom.
Výsledné posúdenie prvkov sa však nevzťahuje na jeden konkrétny extrém vnútornej sily a preto sa rozhodujúce tvary vybočenia a počiatočné imperfekcie pri záverečnom posúdení líšili. Výsledné posúdenie prierezov je výsledkom najnepriaznivejšej kombinácie namáhania. Grafické vyhodnotenie preukázalo, že prírastky vnútorných síl na hlavných oblúkoch konštrukcie dosahujú najväčšie extrémy pri tvaroch vybočenia s označením B1 až B2 s kladnou aj zápornou hodnotou imperfekcie.
10. Záver
Analýza konštrukcie tohto typu je iteračný proces. Po zohľadnení prírastkov vnútorných síl získaných geometricky nelineárnym výpočtom je možné jednotlivým prvkom pri posúdení definovať súčiniteľ vzperu rovný 1,0. V prípade nevyhovujúceho posúdenia je potrebné vo výpočtovom modeli zväčšiť prierez, čo však vedie ku zmene tuhosti a opäť je potrebné znovu vyhľadať tvary vybočenia, vzťahujúce sa na celú konštrukciu. Tie sa nebudú nachádzať na rovnakej pozícii a bude im prisúdený iný koeficient rozdvojenia rovnováhy. Taktiež je potrebné konštatovať, že daná problematika je v tomto konkrétnom prípade vyriešená len čiastočne, nakoľko bolo analyzovaných a vyhodnotených len určitých 256 prípadov z hľadiska vplyvu počiatočných imperfekcii a tvarov vybočenia. Riešenie obdobnej konštrukcie v praxi by si vyžadovalo rozsiahlejšiu analýzu.
11. Literatura
- STN EN 1990: 2007; Eurokód: Zásady navrhovania konštrukcií. August 2009
- [STN EN 1991-1-1: 2007; Eurokód 1. Zaťaženia konštrukcií. Časť 1-1: Všeobecné zaťaženia
- STN EN 1991-1-3: 2007; Eurokód 1. Zaťaženia konštrukcií. Časť 1-3: Všeobecné zaťaženia. Zaťaženia snehom
- STN EN 1991-1-3/NA: 2004; Eurokód 1. Zaťaženia konštrukcií. Časť 1-3: Všeobecné zaťaženia. Zaťaženia snehom. Národná príloha.
- STN EN 1991-1-4: 2007; Eurokód 1. Zaťaženia konštrukcií. Časť 1-4: Všeobecné zaťaženia. Zaťaženia vetrom. Národná príloha.
- STN EN 1991-1-4/NA1: 2010; Eurokód 1. Zaťaženia konštrukcií. Časť 1-4:
- STN EN 1995-1-1: 2008; Eurokód 5. Navrhovanie drevených konštrukcií. Časť 1-1: Všeobecne – Všeobecné pravidlá a pravidlá pre budovy.
- HERDA, Roman. Multifunkčná športová hala. 2021. Diplomová práca. Slovenská technická univerzita v Bratislave, Stavebná fakulta. Vedúci práce Ing. Miloš Slivanský, PhD.
The paper deals with the theoretical shape and stability analysis of a timber grid-shell structure. The peculiarity of the approach to the analysis of this type of construction is manifested in several parts of the design process due to the complicated shape of the roof plane. These specifics can be applied to the initial phase of creating the shape of the structure, which is directly related to the resulting static efficiency of the final design. Other important parts of the structural analysis that deviate from the standard-defined procedures are the determination of the design load by external climatic influences and the stability analysis with the need to apply a geometrically nonlinear calculation with the influence of initial imperfections.
