Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Tuhost vyztuženého panelu vodorovně namáhaného osamělou silou

18.7.2011

Ing. David Mikolášek, VŠB Technická univerzita Ostrava, Fakulta stavební, Katedra stavební mechaniky

Recenzovaný

Hlavní cíl této studie spočíval ve vytvoření a aplikaci výpočtového modelu, který by umožňoval přesnější a objektivnější řešení stěnových panelů namáhaných účinkem horizontálních sil. Z hlediska výztužné funkce panelů v nosných systémech konstrukcí jde o zásadní způsob zatížení.

Stěnové panely jsou základním skladebným a nosným prvkem dřevěných staveb, zejména rodinných a bytových domů, ale i dalších typů pozemních staveb. Práce zaměřené k objektivnější teoretické analýze a k vyhodnocení skutečného působení panelů v reálných konstrukcích mají podstatný význam pro další vývoj dřevěných konstrukcí.

Cílem této numerické studie je zjištění vodorovné tuhosti výztužného panelu z OSB/3 desek tloušťky 12 mm, pro nosnou konstrukci tvořící difuzně otevřenou skladbu, výztužný panel je situován z interiéru.

Studie je řešena jako numerická, tedy výsledkem jsou výstupy matematického modelování dané konstrukce. Tento výztužný panel byl počítán podle normy DIN 1052 a EC5.

Pro zjištění orientačních tuhostních charakteristik, deformací a sil je proveden také ruční výpočet na základě předpokladu lineárního chování materiálu a spojů za pomocí statických rovnic rovnováhy a teorie pružnosti.

Dále jsou popsány tyto varianty výpočtu.

Numerický model detailu řešený v programu ANSYS. Je vytvořen plně 3D konečně-prvkový model s uvážením nelineárního chování materiálu, ortotropie dřeva a OSB/3 panelu. 3D model je počítán fyzikálně a geometricky nelineárně. U 3D modelu v ANSYS je zohledněna kontaktní povaha přípojů, to znamená, objeví se zde jednostranné třecí vazby. Model je zatěžován krátkodobým zatížením (vodorovnou silou). Je sledována deformace a napětí na detailu a ve spoji. Pro tento detail bude vykreslen pracovní diagram znázorňující tuhost výztužného panelu pro jeden spoj. Získané výsledky slouží jako ukázka hodnot vodorovných tuhostí tohoto typu výztužného panelu pro tento typ spoje, pro krátkodobé zatížení bez uvážení cyklického zatěžování.
Ruční přepočet tuhostí a sil podle norem a podle teorie pružnosti slouží jako odborný odhad a zjednodušená kontrola výstupních hodnot z numerických modelů (ANSYS, SCIA). Tento postup je také vhodný pro většinu praktických výpočtů, kdy časové hledisko je nutným faktorem pro optimalizaci náročnosti výpočtu. Mnohdy je také ruční kontrola jedinou možností jak odhadnout chování konstrukce a naladit tímto způsobem numerické modely.
Numerický model v programu SCIA slouží jako kontrola pro ruční výpočet. Byl vytvořen jako 2D skořepinový model s použitím prutových prvků. 2D model je materiálově isotropní, s přihlédnutím k jednostranným vazbám, prokluzům ve spojích (dle DIN 1052) a je počítán geometricky nelineárně. Výsledkem zde jsou reakce ve vnějších vazbách a průběh sil na spojích ("smykový tok" ve spojích) a konečná tuhost pro zadanou zatěžovací vodorovnou sílu.

Závěrem je potřebné podotknout, že každý numerický test by měl být doplněn fyzikálním testem. Bez reálných hodnot ze zkoušek je numerické modelování cenným náhledem na chování konstrukce, ale je nutno ho vždy ověřit fyzikálními testy.

A) Matematický 3D detail spoje v programu ANSYS

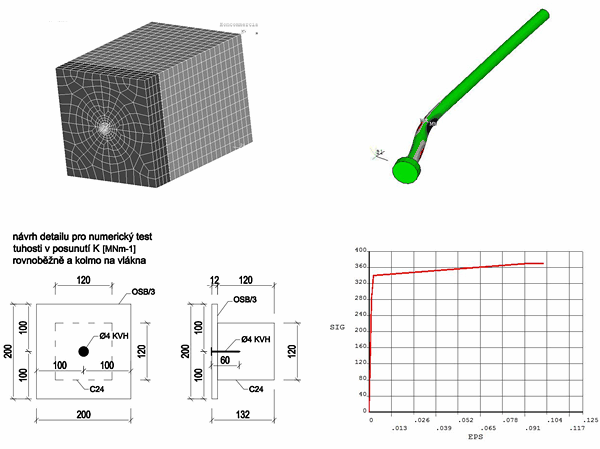
Obr. 1 Schéma numericky testovaného hřebíkového spoje

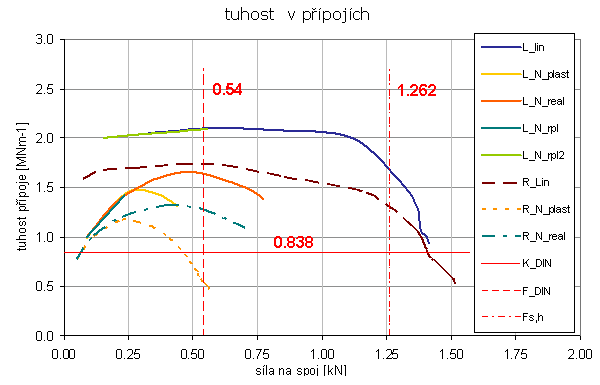
Graf. 1 Graf numerických tuhosti hřebíkového spoje podle ANSYS

Na grafu 1 je znázorněna tuhost pro hřebík S355 ø2.8mm délky 40mm, který spojuje OSB/3 12 mm a s trámky C24 60/140 mm. V numerickém testu (viz obrázek Obr. 1) je znázorněna geometrie testovaného vzorku, deformace spoje a pracovní diagram pro ocel S355. Na grafu Graf 1 je svislou čárkovanou úsečkou zobrazena pevnost hřebíku ø2.8mm podle DIN 1052 a čerchovanou úsečkou pevnost hřebíku ve smyku pro F_u,k=F_y,k =355MPa. V tomto stavu hřebík plně plastizuje. Sice není dosaženo porušení hřebíku ø2.8 mm cca 1.262 kN, ale spoj je natolik duktilní, že již není schopen přenášet další zatížení. Vodorovná plná úsečka o hodnotě 0.838MNm^-1 představuje tuhost proti posunutí podle DIN 1052.

Na grafu je několik křivek, křivky s označením indexem "L" jsou tuhosti pro zatěžování rovnoběžně s vlákny a "R" je zatěžování kolmo na vlákna. Podle výpočtu tuhostí podle DIN 1052 a EC5 se pro kolíkové spoje tohoto průměru neuvažuje změna tuhosti s ohledem na orientaci síly ke vláknům. Podle numerického testu je tuhost závislá na orientaci síly ke vláknům.

Každém testu uvedeném na grafu Graf 1 je ocel počítána jako fyzikálně nelineární (pružno-plastická) podle Obr. 1 vpravo dole. Křivka s označením L_lin je tuhost rovnoběžně s vlákny pro ortotropní dřevo 24 a OSB/3. Je zde vidět, že hřebík začíná silně plastizovat. Další křivky s indexem "L" jsou pro různé varianty ortotropního dřeva C24 a OSB/3 s různými parametry fyzikální nelinearity. Můžeme zde pozorovat na různých křivkách L_N závislost tuhosti nejen na ocelovém hřebíku, ale také na plastizaci okolí dřevěného prvku a OSB. Tyto výpočty nevedou na silně duktilní chování spoje. Numerický model je citlivý na překročení nastavení plastizace v lokálních bodech, a proto nedojde k pokračování grafu - plastizace spoje, ale výpočet je ukončen, i když u reálného spoje by zatěžování pokračovalo dál (dřevo se lokálně otlačí - poruší, ale spoj má stále určitou tuhost, nedojde k porušení celku), skutečný spoj bude zatěžován až do úplné plastizace ocelového spoje.

Křivka s označením R_lin je tuhost kolmo na vlákna pro ortotropní dřevo 24 a OSB/3. Je zde vidět, že hřebík začíná silně plastizovat. Další křivky s indexem "R" jsou pro různé varianty ortotropního dřeva C24 a OSB/3 s různou fyzikální nelinearitou. Můžeme zde pozorovat na různých křivkách R_N závislost tuhosti nejen na ocelovém hřebíku, ale také na plastizaci okolí dřevěného prvku a OSB/3. Tyto grafy opět nevedou na silně duktilní chování spoje, ale jsou blíže ke křivce L_lin, protože tuhost kolmo na vlákna je menší vlivem ortotropních vlastností dřeva. Dosahuje se zde menších lokálních napětí než pro zatěžování rovnoběžně s vlákny. Numerický model je také citlivý na překročení nastavení plastizace v lokálních bodech a proto nedojde k pokračování grafu - plastizace spoje, ale výpočet je ukončen, i když u reálného spoje by zatěžování pokračovalo dál (dřevo se lokálně otlačí - poruší, ale spoj má stále určitou tuhost, nedojde k porušení celku), skutečný spoj bude zatěžován až do úplné plastizace ocelového spoje.

Z grafu 1 je vidět, že rozdíl mezi L_lin a R_lin, R_lin je cca 1.25 násobek L_lin. Je to způsobeno právě ortotropií dřeva (rozdínými moduly pružnosti pro rovnoběžný cca 10GPa a kolmý cca 0.9GPa směr zatěžování).

Normová charakteristická tuhost má hodnotu K_ser =0.838MNm^-1 viz 3.3). Tato hodnota je nejblíže ke křivce R_lin ≈ 1.70MNm^-1. Pokud přihlédneme k cyklickému zatěžování a nepřesnostem při provádění atd. dá se konstatovat, že normová hodnota tuhosti proti posunutí se blíží spíše k hodnotě pro zatěžování kolmo na vlákna.

Tuhosti pro numerické modely vycházejí obecně vyšší, a to z důvodu, že se neuvažuje cyklické zatěžování (otlačování, plastické deformace spojů). Poměr krátkodobých tuhostí jednostřižného spoje v posunutí podle matematických modelů bez příhlédnutí k otlačování dřeva a OSB panelu K_ser= (1.7+2.1)/2=1.9MNm^-1 jsou tedy 2 až 2.5 násobkem charakteristické tuhosti v posunutí podle DIN 1052 K_serDIN = (1.7+2.1)/2=0.838MNm^-1.

B) Ruční výpočet výztužného panelu

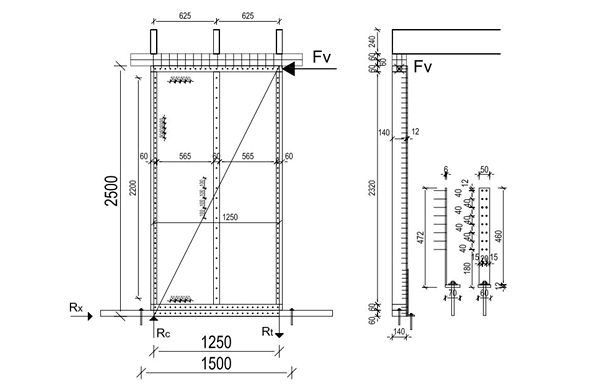
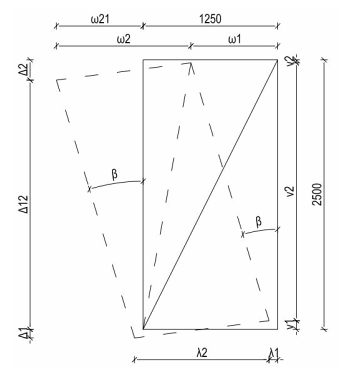
Obr. 2 Geometrie a zatížení výztužného panelu

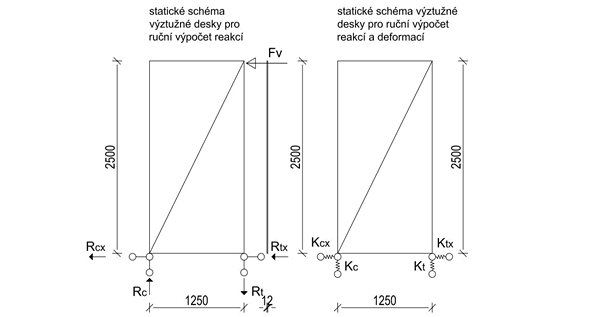
Obr. 3 Schéma geometrie výztužného panelu

Na obrázku Obr. 3 vidíme schéma geometrie výztužného panelu, které použijeme pro výpočet reakcí ručním výpočtem. Pro výpočet reakcí použijeme levou část obrázku, kde jsou všechny vazby dokonale tuhé. Úloha je jednou staticky z vnějšku neurčitá, a to vodorovnou vazbou v ose x. Z předpokladu stejného posunutí spodního prahu C24 60/140 se dá říci, že reakce vodorovné jsou stejné. Úloha představuje v principu konzolu, kde vetknutí nahrazuje dvojice sil. Druhý obrázek vpravo je dokreslení představy, že vazby ve skutečnosti nejsou dokonale tuhé, ale jsou to pružné vazby se svou tuhostí, kterou lze dopočítat na základě rovnic pružnosti (předpokládáme lineární chování materiálu, platí Hookův zákon).

Výpočet reakcí podle Obr. 3

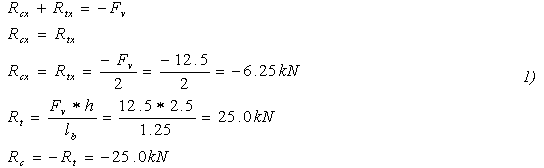
Reakce byly vypočteny na základě třech statických podmínek rovnováhy.

Výpočet únosností hřebíků ø2.8mm na jeden střih ve sloupech C24 60/140 a vodorovných žebrech C24 60/140 podle DIN 1052.

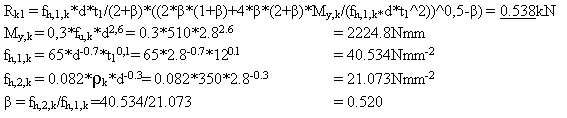
Hodnota únosnost hřebíku ø2.8mm je stanovena podle DIN 1052 na 0.538kN. Tato hodnota byla spočtena pro jeden vztah dle DIN 1052, obecně se musí vyřešit všechny vztahy a z nich vybrat minimální únosnost hřebíku. Výše uvedený vztah je vybrané minimum z těchto vztahů a jejich hodnot. Jde o charakteristickou hodnotu, nejsou použity součinitele materiálu ani třídy prostředí atd. Hodnota únosnosti je uvažována pro střih ocel a C24 60/140.

Výpočet únosností hřebíků ø4mm na jeden střih ve sloupech C24 60/140 DIN 1052.

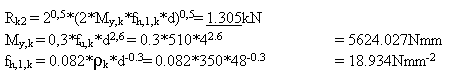
Hodnota únosnosti hřebíku ø4mm je stanovena podle DIN 1052 na 1.305kN. Tato hodnota byla spočtena pro jeden vztah dle DIN 1052, obecně se musí vyřešit všechny vztahy a z nich vybrat minimální únosnost hřebíku. Výše uvedený vztah je vybrané minimum z těchto vztahů a jejich hodnot. Jde o charakteristickou hodnotu, nejsou použity součinitele materiálu ani třídy prostředí atd. Hodnota únosnosti je uvažována pro střih ocel a C24 60/140.

Nutný počet hřebíku do sloupků C24 60/140 je :
n_h3 = R_t/R_k1=25/0.538 = 47 hřebíků ø2.8mm ocel S355

Nutný počet hřebíku do sloupků C24 60/140 přes ocelovou kotvu je :
n_h2 = R_t/R_k2=25/1.305 = 20 hřebíků ø4mm ocel S355

Nutný počet hřebíku do vodorovných žeber C24 60/140 je :
n_h = F_v/R_k1=12.5/0.538 = 24 hřebíků ø2.8mm ocel S355

Hřebíky mají ještě cca 25% rezervu únosnosti do porušení, proto je použito pro sloupky a ocelové kotvy 16 hřebíků ø4mm. Důvodem je proveditelnost a skrytost ocelového spoje.

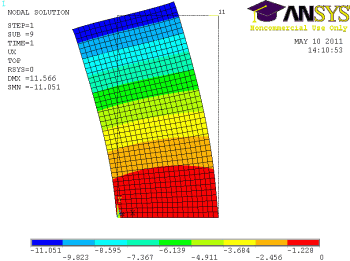Obr. 4 Deformace ve směru vodorovné osy x vazby po celé délce

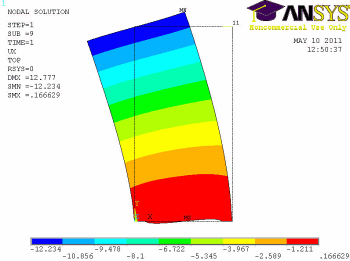Obr. 5 Deformace ve směru vodorovné osy x vazba v rozích

Deformace ve vodorovné ose x od síly v žebru viz Obr. 3. Na obrázku Obr. 4 vlevo je znázorněna deformace pro tuhé podepření v ose z, takto podepřená výztužná deska v reálné konstrukci není. U reálné konstrukce je uchycena pružně v místech napojení na tahové a tlakové kotvy v rozích. Vpravo Obr. 5 je výztužná deska uchycena v rozích. Skutečná konstrukce se svými vnějšími vazbami je něco mezi těmito limitními případy.

Podle zjištěných deformací pro sílu F=12.5kN pro model s neposuvnou hranou v ose z u_xmax=11.051mm a pro model s vazbami v rozích vpravo s deformací u_xmax=12.234mm se dá konstatovat, že pro oba zvolené modely je deformace podobná a ruční výpočet deformace podle teorie pružnosti silovou metodou je v dobré shodě s numerickými modely.

Numerické modely byly počítány jako ortotropní a geometricky nelineární (jako skořepina a objemový konečný prvek, na obrázcích je výsledek na skořepinovém konečném prvku). Když byla do úvahy vzata též geometrická nelinearita, nebylo zjištěno výrazné zvětšení deformací. Pouze, takto uložená výztužná deska o síle 12 mm je velmi citlivá na příčné zatížení a excentrické zatížení (v takovém případu může pro limitní vodorovnou sílu dojít ke ztrátě stability).

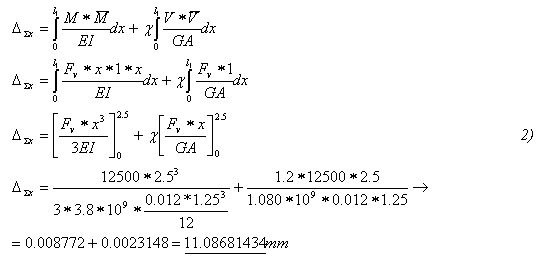
Vzorec 2) popisuje výpočet deformace konzoly silovou metodou používanou pro pruty. Jde o vodorovnou deformaci od vodorovné síly na horním okraji výztužné desky.

Tato úloha svou geometrií se již nedá považovat za prutovou. Ale na základě srovnání výsledků na skořepinách s ručním výpočtem, je možno deformace od posouvajících sil (zkosení) a ohybových momentů (natočení) počítat jako na prutech i pro tento výztužný panel podle teorie pružnosti a základních rovnic statiky.

Takto spočtená deformace je v dobré shodě s numerickou hodnotou viz Obr. 4 a 5.

Tento výsledek nám dovoluje používat zjednodušení při výpočtu deformací výztužného panelu, který má charakteristiky stěny, ale lze jej pro tento případ okrajových podmínek, geometrie a zatížení počítat jako prutový prvek.

OSB/3 materiálové charakteristiky podle ČSN EN 13986 (podle ČSN EN 12369-1)

12mm síla materiálu panelu
I. třída použití
k_mod = 1 součinitel délky trvání zatížení (standardně 0.9)
ν_M = 1 součinitel pro materiál (standardně 1.3)

Tyto hodnoty součinitelů budou použity také pro C24 rostlé řezané dřevo.

OSB/3 panel má pro různý smysl zatěžování (kolmo na rovinu desky a v rovině desky) různé materiálové charakteristiky. Dále se musí uvážit orientace částic, štěpek v povrchové vrstvě a síla panelu. Orientace částic v povrchové vrstvě má význam pro tuhosti, pro E a G moduly pružnosti.

Pro skořepinový 2D a objemový 3D model byly zvoleny tyto tuhostní a pevnostní charakteristiky (OSB/3 a RD C24 rostlé dřevo).

Tyto hodnoty Tab. 1 pro model v ANSYS byly převzaty z literatury Engineering Structure [4]. Hodnoty pro OSB/3 byly porovnány s hodnotami podle DIN 1052 a byly vzaty pro ortotropní matematický model.

index	Ortotropní vlastnosti	RD - rostlé dřevo	Výztužná deska	Jednotky
index	Ortotropní vlastnosti	C24	OSB/3
1	E_x	10500	3800	[MPa]
2	E_y	900	2600	[MPa]
3	E_z	500	130	[MPa]

4	γ_xy	0.370	0.184	[ - ]
5	γ_yz	0.430	0.312	[ - ]
6	γ_xz	0.470	0.364	[ - ]

7	G_xy	750	1080	[MPa]
8	G_yz	39	50	[MPa]
9	G_xz	720	50	[MPa]

Tab.1 vlastnosti použité v matematických modelech pro ANSYS

Pevnostní vlastnosti budou uvažovány pouze v charakteristických hodnotách podle DIN 1052. Tyto hodnoty jsou ale samozřejmě menší než fyzikální hodnoty porušení jednotlivých materiálů. Tato skutečnost nebude pro ruční výpočet brána do úvahy, pouze u matematického modelu s uvážením fyzikální nelinearity bude použita hodnota meze pevnosti vyšší, je to způsobeno vlivem plastizace (přerozdělení sil) nad mezí kluzu (neplatí pro křehké porušení - tah, tah kolmo na vlákna, částečně smyk). Charakteristická hodnota bude v matematických modelech brána jako mez kluzu.

index	Pevnostní vlastnosti	Zatížení podle smyslu	Rostlé dřevo charakteristické hodnoty	Hodnoty pevnosti	Výztužná deska charakteristické hodnoty	Hodnoty pevnosti	Jednotky
index	Pevnostní vlastnosti	Zatížení podle smyslu	C24		OSB/3 12mm
1	f_m,k	Ohyb ⊥	24,0	60	16,4	18,8	[MPa]
2	f_c,90,k	Tlak ⊥	2,5	4	10,0	15	[MPa]
3	f_v,k	Smyk ⊥	2,5	3	1,0	2	[MPa]
3.4	f_t,90,k	Tah ⊥	0,4	2	1.0	2
4	f_m,k	Ohyb =	24,0	60	9.4	16.8	[MPa]
5	f_t,k	Tah =	14,0	40	9.4	12	[MPa]
6	f_c,k	Tlak =	21,0	34	15.4	20	[MPa]
7	f_v,k	Smyk =	4,0	7	6.8	8	[MPa]
8	ρ_k	Hustota	350	350	550	550	[kgm^-3]

Tab.2 vlastnosti použité v matematických modelech pro ANSYS a pro ruční kontrolu

Pro tah kolmo na vlákna, který se chová velmi křehce, je hodnota pevnosti cca 5 x vyšší než charakteristická. Je to především proto, že tato vlastnost je velmi složitě zachytitelná ve výpočtu a její hodnota nabývá různých velikostí, podle různých faktorů (dřevo je přírodní materiál se všemi výhodami, ale také pro technické využití s určitými nevýhodami - nehomogenní vlastnosti ať už v podobě mechanických vlastností, nebo vnitřní geometrie, suky atd.). Meze pevnosti jsou zvoleny odborným odhadem.

Výpočet deformací a tuhosti pomocí ručního výpočtu:

I) Zjednodušující předpoklady

materiál je bez imperfekcí
platí Hookův zákon (fyzikální linearita)
deformace neovlivní přerozdělení vnitřních sil (geometrická linearita)
materiál je homogenní, isotropní
zatížení se zvětšuje tak, že nevyvodí dynamické účinky
geometrie je zjednodušena na osy, nejsou zde excentricity zatížení ani vazeb
nejsou uvažovány počáteční prokluzy ve spojích (dokonalý počáteční kontakt)
tlačená a tažená strana budou mít stejné deformace ve svislé ose (teoretický předpoklad)
zatížení je krátkodobé, nejsou uváženy cykly, prostředí je třídy I.

II) Postup výpočtu
deformace ve vodorovném směru se získá sečtením jednotlivých příspěvků od jednotlivých komponentů které spolu vytvářejí výztužný panel OSB/3

posun ocelové kotvy vlivem ohybu u chemické kotvy ↑
natažení sloupku 60/140 C24 a OSB/3 ↑
prokluz hřebíků ø4mm tahové kotvy pro sloupek 60/140 C24 + natažení ocelového plochého prvku ↑
prokluz hřebíků ø2.8mm pro sloupek 60/140 C24 a OSB/3 ↑
skosení a natočení OSB/3 panelu ←
prokluz hřebíků ø2.8mm pro vodorovné trámky 60/140 C24 a OSB/3 ←
stlačení vodorovného trámku C24 a OSB/3 ←
prokluz chemických kotev ø12mm ←
tření mezi spodním prahem trámku 60/140 C24 má součinitel klidového tření ζ=0.4 (beton dřevo), neuvažuje se v ručním výpočtu (bránění vodorovné deformaci

Suma svislých deformací

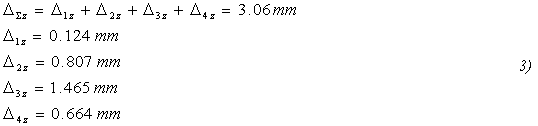
1) Deformace Δ_1z představuje svislou deformaci ohybově deformovaného kotvení chemické kotvy pro plochou ocel.

Δ_1z= F_v*h/l_b*l_e³/ (3*E_steel* I_steel) = 12500*2.5/1.25*0.033/(3*210*109*1/12*0.06*0.012³) = 0.1245mm

2) Deformace Δ_2z představuje svislou deformaci nataženého sloupku 60/140 C24 a OSB/3 panelu.

Δ_2z = F_v*h/l_b*h/(3*E_C24*A_C24)+F_v*h/l_b*h/(3*E_xOSB*A_xOSB) = 12500*2.5/1.25*2.5/(3*10.5*109*0.06*0.140)+12500*2.5/1.25*2.5/(3*3.8*109*0.012*0.80)= 0.807mm

3) Deformace Δ_3z představuje svislou deformaci od prokluzu hřebíků ø4mm spojující OSB/3 panel se svislým žebrem 60/140 C24 a svislou deformaci od protažení ploché oceli.

K_ser = ρ_k12^1,5*d^0,8/25 = ((350*550)^0.5)^1.5*4^0.8/25 = 1114.374Nmm^-1

K_ser - představuje tuhost proti posunutí na jeden střih pro nepředvrtaný hřebík ø4mm podle DIN 1052.

4) Δ_3z = F_v*h/l_b*(n_h2*K_ser) + F_v*h/l_b*l_steel/(3*E_steel2*A_steel2) = 12500*2.5/1.25/(16*1.114*10⁶)+ 12500*2.5/1.25*0.470/(3*210*10⁹*0.05*0.006)= 1.465mm

Deformace Δ_4z představuje svislou deformaci od prokluzu hřebíků ø2.8mm spojující OSB/3 panel se svislým žebrem 60/140 C24.

K_ser = ρ_k121,5*d^0,8/25 = ((350*550)^0.5)^1.5*2.8^0.8/25 = 837.74Nmm^-1

K_ser - představuje tuhost proti posunutí na jeden střih pro nepředvrtaný hřebík ø2.8mm podle DIN 1052.

Δ_4z = F_v*h/l_b*(n_h3*K_ser) = 12500*2.5/1.25/(45*0.837*10⁶) = 0.664mm

Suma vodorovných deformací

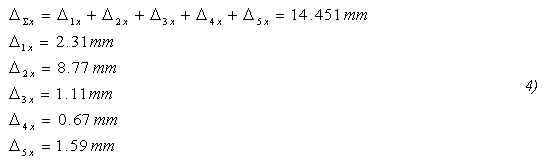
5) Deformace Δ_1x představuje vodorovnou deformaci od ohybu a Δ_2x představuje vodorovnou deformaci od posouvající síly, smyku (zkosení) viz rovnice 1).

6) Deformace Δ_3x představuje vodorovnou deformaci od prokluzu hřebíků ø2.8mm spojujících horní a dolní okraj OSB/3 panelu s vodorovnými žebry 60/140 C24.

K_ser = ρ_k12^1,5*d^0,8/25 = ((350*550)^0.5)^1.5*2.8^0.8/25 = 837.74Nmm^-1 3.3)

K_ser - představuje tuhost proti posunutí na jeden střih pro nepředvrtaný hřebík ø2.8mm podle DIN 1052

Δ_3x = 2*F_v/ (n_h*K_ser) = 2*12500/(25*0.87374*10⁶) = 1.1445mm

7) Deformace Δ_4x představuje vodorovnou deformaci stlačených vodorovně spojovaných žeber 60/140 C24 a OSB/3 panelu.

Δ_4x = 2*F_v*l_b/(3*E_C24*A_C24)+2*F_v*l_b/(3*E_yOSB*A_yOSB) = 2*12500*1.25/(3*10.5*10⁹*0.06*0.140)+2*12500*1.25/(3*2.6*10⁹*0.012*0.60)=0.674mm

8) Deformace Δ_5x představuje vodorovnou deformaci od prokluzu chemických kotev ø12mm. Spojující OSB/3 panel jako celek s vodorovnou železobetonovou konstrukcí.

K_ser = ρk^1,5*d/20 = 350^1.5*12/20 = 3928.74Nmm^-1

K_ser - představuje tuhost proti posunutí na jeden střih pro přesný svorník, kolík ø12mm podle DIN 1052.

Δ_5x = F_v/ (n_s*K_ser) = 12500/(2*3.928*10⁶) = 1.591mm

Výsledná suma vodorovných deformací a svislých deformací (svislé deformace způsobí deformaci také ve vodorovném směru, tato deformace bude mít označení Δ_Σzx).

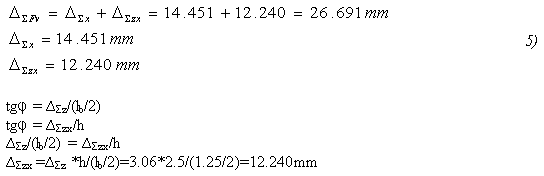
Tuhost výztužného panelu OSB/3 12mm 1250/2500 (Obr. 2) ve vodorovném směru podle ručního výpočtu.

Ve výše uvedeném vztahu 6) je vypočítána tuhost výztužného panelu OSB/3 o síle 12mm jednostranně připojeného pomocí hřebíků ø2.8mm k žebrům z hranolků C24 60/140. Hranolky C24 60/140 jsou potom připojeny pomocí hřebíků ø4mm ke ocelovému profilu z ploché oceli a ten je připojen chemickou kotvou do spodní železobetonové konstrukce.

C) Numerický výpočet výztužného 2D panelu v programu SCIA

Numerický model ve SCIA je 2D prutový model spojený skořepinovými prvky. Jsou zde zohledněny pružné vazby, jednostranné vazby a geometrická nelinearita. Panel OSB/3 musel být spočítán ve SCIA jako ortotropní. Tato volba musí být zatrhnuta ve volbě okna pro materiálové charakteristiky a geometrii. Pokud tento panel nebude počítán jako ortotropní, tak SCIA nebude uvažovat pro skosení od posouvající síly správný smykový modul, který je cca 2 x menší než Youngův modul pružnosti.

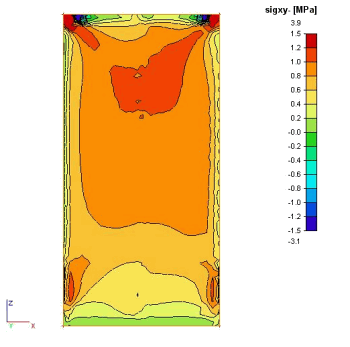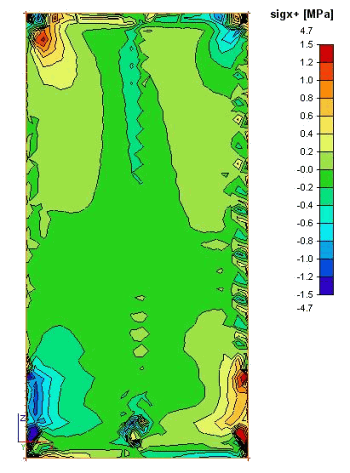
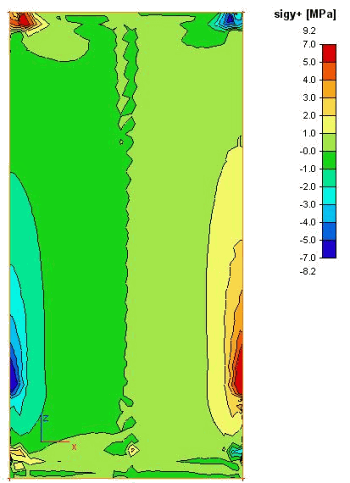
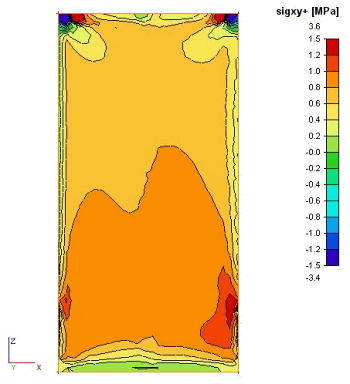
Obr. 6 Napětí na OSB/3 panelu

Na obrázcích 6 jsou napětí na OSB/3 výztužném panelu. První obrázek v levém horním rohu představuje normálové napětí S_x, které je rovnoběžné se spodní hranou panelu. Druhý obrázek v pravém horním rohu představuje normálové napětí S_y, které je rovnoběžné se svislou hranou panelu. Zde je vidět ohybové namáhání na konzole (dvojice sil je realizována ve sloupcích, panel je smýkán), napětí v tlaku a tahu dosahuje hodnot cca 8 MPa (charakteristická hodnota pevnosti v tahu podle DIN 1052 je f_t,k=9.4 MPa a v tlaku f_c,k=15.4 MPa).

Spodní dva obrázky představují smykové napětí S_xy+ a S_xy-, hodnoty dosahují velikosti cca 1.50 MPa (charakteristická hodnota podle DIN 1052 je f_v,k=6.8 MPa) mimo lokality způsobené hustotou sítě, geometrií a lokálním, uzlovým vnesením osamělé síly.

Panel byl tedy navrhován na maximální využití spojů a výztužné desky v charakteristických hodnotách, je nutné dodat, že fyzikální únosnost celku je ještě cca 1.5-2x vyšší (zde, ale nejde už o pružnou oblast, panel a spoje jsou nevratně poškozeny).

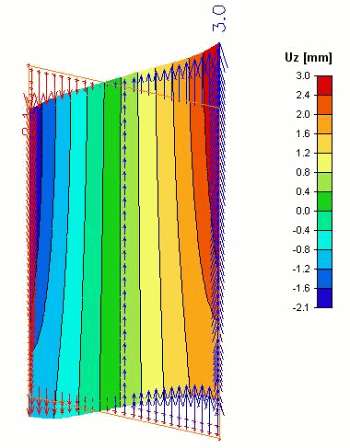
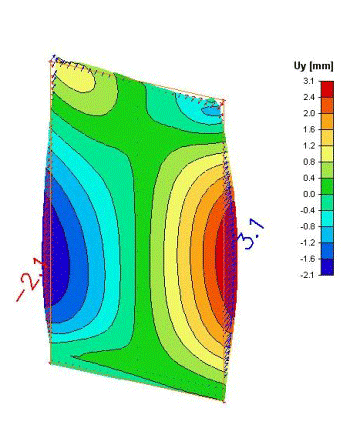
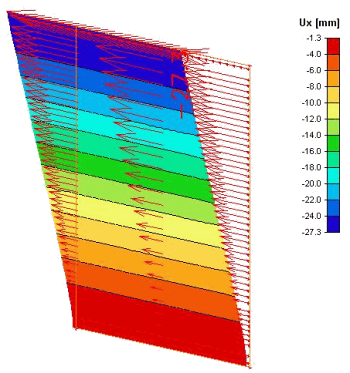
Obr. 7 Deformace OSB/3 panelu - axonometrie

Na obrázcích 7 jsou deformace na OSB/3 panelu. První obrázek v levém horním rohu představuje deformaci svislou U_z = (+3.0mm, -2.1mm), které je rovnoběžné se svislou hranou panelu. Druhý obrázek v pravém horním rohu představuje deformaci kolmou na rovinu panelu U_y = (+3.1mm, -2.1mm). Třetí obrázek představuje deformaci vodorovnou U_x = -27.3mm, -1.3mm), které je rovnoběžné se spodní hranou panelu. Čtvrtý obrázek znázorňuje představu o deformaci panelu.

D) Závěr

Výsledné tuhosti proti posunutí

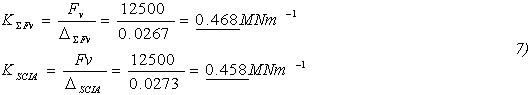
Hodnoty podle vztahu 7) jsou pro numerický model a ruční výpočet shodné na cca 97.8 %. To znamená, že výztužnou tuhost panelu lze určit s dostatečnou přesností ručním výpočtem. Tyto tuhosti byly určeny za předpokladu normových prokluzů podle DIN 1052. Pokud bychom vzali do úvahy vyšší tuhosti spojovacích prostředků získaných podle ANSYS (Graf. 1) pro krátkodobé, necyklické zatížení, dostali bychom tuhost o něco vyšší cca 0.593MNm^-1. Velký vliv na tuhost pro všechny modely zde hraje zkosení panelu OSB/3, tedy jeho smyková tuhost G_xy = 1080MPa.

Byly také vyzkoušeny dvě různé hustoty prohřebíkování v krajních sloupech (50 a 100mm). Na modelu v programu SCIA bylo zjištěno lineární chování tuhosti na hustotě prohřebíkování. Je třeba dodat, že hustota hřebíků průměru 2.8mm po 50mm je již téměř limitní jak z pohledu provádění tak i pevnostního. Vyšším počtem spojovacích prostředků tohoto typu nedocílíme vyšší tuhosti proti posunutí. Citlivým místem se naopak stane kotvení velkých sil do spodní konstrukce. Mimo to lokální vnášení sil u podpor je na hranici normové pevnosti jednostranného OSB o síle 12mm.

Numerický model nám dává poměrně výstižný způsob popisu chování konstrukce pro silové, nebo deformační zatížení. A díky získaným datům (síly a deformace), můžeme získat tuhostní charakteristiky také pro jinou sestavu výztužných panelů. Tímto způsobem lze určit s dobrou přesností potřebné fyzikální veličiny potřebné pro další výpočty.

Literatura

[1] ČSN 73 1702 mod DIN 1052:2004
[2] Uživatelská dokumentace programu SCIA, 2008.
[3] ANSYS 10 Documentation. ANSYS Inc., 2005.
[4] Z.W. Guan, E.C. Zhu, Finite element modelling of anisotropic elasto-plastic timber composite beams with openings, Engineering Structure 31 (2009) 394-403.

Poděkování

Tento výsledek byl získán za finančního přispění MŠMT ČR, projekt 1M0579, v rámci činnosti výzkumného centra CIDEAS.

Recenzní posudek příspěvku
Ing. David Mikolášek

TUHOST VÝZTUŽNÉHO PANELU
Tuhost výztužného panelu vodorovně namáhaného osamělou silou

Příspěvek je zaměřen k analýze horizontální tuhosti výztužných stěnových panelů s dřevěným orámováním a opláštěním z deskových materiálů na bázi dřeva. Oplášťující vrstva panelu je provedena z desek typu OSB.

Vyjádření k aktuálnosti tématu příspěvku

Zásadním bodem předloženého příspěvku je především podrobné numerické řešení výztužných stěnových panelů na základě matematického modelování panelu a srovnání výsledků tohoto řešení s odpovídajícími výsledky získanými zjednodušenými metodami ve smyslu současných norem pro navrhování dřevěných konstrukcí.

V současné době není problematika skutečného chování výztužných panelů z hlediska teoretického a experimentálního výzkumu, zejména s uvážením vlivu reologie materiálů, poddajnosti spojů a dlouhodobého působení účinků zatížení, ještě dostatečně vyšetřena.

Z výše uvedených důvodů považuji autorem zpracované téma za aktuální a perspektivní a publikaci výsledků za přínosnou.

Vyjádření ke splnění předpokládaného cíle a zvoleným výpočtovým metodám

Hlavní cíl studie spočíval ve vytvoření a aplikaci výpočtového modelu, který by umožňoval přesnější a objektivnější řešení stěnových panelů namáhaných účinkem horizontálních sil. Z hlediska výztužné funkce panelů v nosných systémech konstrukcí jde o zásadní způsob zatížení.

Pozitivně hodnotím, že autor v rámci studie vyřešil tři varianty výpočtu panelu a konkrétní výsledky řešení podrobně dokumentuje v předloženém příspěvku.

Z hlediska praktického využití je důležité srovnání výsledků získaných na základě numerických modelů (varianta A a C) s výsledky vycházejícími ze zjednodušených postupů podle norem pro navrhování dřevěných konstrukcí (varianta B).

K analýze problému autor aplikoval metody umožňující objektivnější vyšetřování panelů, včetně podstatného vlivu únosnosti a poddajnosti spojení oplášťující desky s rámem panelu.

Reprezentativní typ panelu je vhodně zvolen. Volba základních materiálů, geometrické parametry panelu, způsob jeho uložení, druh spojovacích prostředků a jejich rozmístění odpovídají typu, který je používán v reálných konstrukcích.

Postup řešení tématu je vhodně zvolen a logicky uspořádán. V příspěvku je uvedena přehledná a výstižná charakteristika metod použitých k výpočtu panelu. Popis veličin a uvedení číselných výsledků řešení v textu je přínosné. Prokazuje důslednost autora při zpracování příspěvku a umožňuje velmi dobrou orientaci v textu. Konstatuji, že cíl, který je uveden v úvodu příspěvku, autor splnil.

Vyjádření k výsledkům studie a získaným poznatkům

Příspěvek je podložen výsledky komplexního řešení stěnového panelu a obsahuje vlastní přístupy, stanoviska a závěry autora. Zjednodušující předpoklady, které autor v příspěvku uvádí, jsou z hlediska řešení daného problému přijatelné. Zařazení srovnávacích výsledků řešení výpočtových modelů je účelné. Autor prokázal, že výsledky získané řešením přesnějších modelů jsou v dobrém souladu s výsledky získanými řešením podle noremních postupů, což je velmi důležité z hlediska praktického navrhování konstrukcí, jejichž prostorová stabilita je zajišťována výztužnými stěnovými panely

Práce zaměřené k objektivnějšímu posuzování stěnových a deskostěnových panelů mají podstatný význam pro vývoj dřevěných konstrukcí i hodnocení stávajících konstrukcí. Základní postup a metodika, které autor aplikoval při řešení tématu, mohou být uplatněny i obecněji při analýze dalších typů panelů s opláštěním na bázi sádrovláknitých desek, lamelových desek a dalších materiálů vhodných pro opláštění panelů.

Závěr, který autor uvádí v příspěvku, že "každý numerický test by měl být doplněn fyzikálním testem", je samozřejmě správný. Prací zaměřených k experimentálnímu výzkumu panelů a výsledků testů existuje mnoho, výzkum v této oblasti však stále pokračuje a nesporně patří k perspektivním. Výsledky teoretických řešení jsou pro srovnání a navrhování panelů nezbytné, což uvádí také autor příspěvku. Závěr autora, vztahující se k limitnímu počtu spojovacích prostředků, je správný. Hodnota rozteče 50 mm je prakticky limitní pro všechny druhy mechanických spojovacích prostředků. Rozhodující je už pak zpravidla nikoliv únosnost a tuhost spojení, ale namáhání dřeva kolmo na vlákna, případně i opláštění v oblasti podpor, jak autor v příspěvku uvádí.

Vyjádření k formální úpravě příspěvku

Příspěvek je i po formální stránce dobře zpracován. Text je přehledně a logicky uspořádán. V závěru jsou shrnuty podstatné poznatky. Způsob zpracování příspěvku odpovídá požadavkům na zpracovávání odborně-vědeckých prací. Text je podrobně doplněn grafickou dokumentací, zpracovanou na velmi dobré úrovni. Práce obsahuje seznam obrázků, seznam tabulek i přehled použitých symbolů. Vztahy jsou přehledné, použitá literatura je v práci uvedena (snad jen u citovaných norem bych uvedl kromě čísla i název norem). Konstatuji, že i po formální stránce je příspěvek velmi dobře zpracován.

Závěrečné zhodnocení příspěvku z hlediska publikace

Příspěvek je zaměřen k aktuální a perspektivní tématice a obsahuje nové poznatky vztahující se k řešení stěnových panelů. Na základě podrobnějšího hodnocení, uvedeného výše, považuji příspěvek za přínosný. Doporučuji příspěvek Ing. Davida Mikoláška k publikaci.

English Synopsis

The main objective of this study was to develop and apply computational model that would allow more accurate and objective solution of wall panels subjected to horizontal forces. In terms of reinforcing function of panels in the construction of supporting systems it is a fundamental way of load.