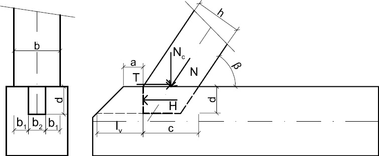
Analýza šikmého středního čepování s krátkým zhlavím
Předmětem tohoto článku je analytická, numerická a experimentální analýza šikmého středního čepovaní s krátkým zhlavím a konfrontace zjištěných napětí s charakteristickými pevnostmi, používanými při posuzování napjatosti tesařských spojů podle Eurokódu 5.
1. Úvod
Tesařské spoje patří mezi nejstarší spoje dřevěných konstrukcí. Tyto spoje vyžadují kvalitní provedení a jejich nevýhodou je, že oproti ostatním spojům dřevěných konstrukcí velmi oslabují konstrukční prvky a jsou pracné. Naši předkové uměli tesařské spoje provádět velice pečlivě. Nikdy je však nepočítali a uplatňovali takzvané zkušenostní navrhování. Při rekonstrukcích proto velmi často narážíme na problém, jak tyto spoje posuzovat – návrhové metodiky ve většině případů chybí. Tesařské spoje, nejčastěji plátování průběžného dřevěného prvku, osedlání krokve na pozednici, čepování sloupku do vaznice nebo ostřihové čepování krokví v hřebeni střešní konstrukce, jsou ve velké míře prováděny i v současné stavební praxi. Návrh tesařského spoje obvykle vychází z empirických vztahů a jednoduchých analytických předpokladů, ojediněle je výpočet podpořen normovým postupem. Proto je velmi aktuální se těmto spojům věnovat.
2. Analytický model
Jednoduchý analytický postup výpočtu šikmého středního čepování uvádí Vinař [3]. Dále představená metoda je oproti uvedenému odkazu geometricky zobecněna a použitelná je nejen pro spoj s doporučenými rozměry.
Napětí kolmo k vláknům vlivem působení složky normálové síly Nc na ploše Ac1 (mezi čelem prvku s čepem a prvku s dlabem):
Vodorovná síla H je rozdílem vodorovné složky normálové síly a třecí síly. Součinitel tření v klidu dřeva po dřevě je uvažován podle [3] µ0 ≈ 0,353. Vodorovná síla H působí na stěnu dlabu směrem ke zhlaví prvku. Hrozí usmyknutí bloku dřeva účinkem smykového napětí rovnoběžně s vlákny na smykové ploše Av1 (tři plochy od dlabu ke konci zhlaví):
Čelo čepu, které se opírá o stěnu dlabu směrem ke zhlaví, je otlačováno napětím šikmo k vláknům vodorovnou silou H na ploše Ac2 (mezi čelem čepu a stěnou dlabu):
Smykové napětí v průřezu čepu od vodorovné síly H na ploše Av2 (smyková plocha čepu):
Obecně analytický model slouží k porovnání podle něho zjištěného napětí s normovou/návrhovou pevností. V případě pevnosti dřeva je přitom potřeba brát v úvahu směr namáhání vzhledem ke směru jeho vláken. Velikost návrhové pevnosti konstrukčního dřeva závisí nejen na třídě pevnosti (kvalitě) dřevěného prvku ale i na délce trvání zatížení a třídě provozu, do které je prvek zabudován. V tomto článku jsou hodnoty napětí, zjištěné analytickým modelem, porovnány s přípustnými napětími při dodržení míry spolehlivosti podle Eurokódu 5 [4].
3. Numerický model
V článku prezentovaná numerická simulace tesařského spoje je založena na předpokladu lineárního ortotropního modelu dřeva. Čepované spojení prvků je zatíženo silou F = 100 kN, která se pohybuje v elastické oblasti chování dřeva. Celý spoj je rozdělen na isoparametrické šestistěnné elementy s dvaceti uzlovými body. V oblasti styku obou spojovaných dřevěných prvků je vytvořena kontaktní plocha s definovanou hodnotou statického součinitele smykového tření µ0 ≈ 0,353, viz výše. Velikost sítě je nastavena na velikost prvku 10 mm a v oblasti kontaktu a ve zhlaví je síť zjemněna na hodnotu 5 mm. Celkem je modelováno 18527 elementů.
4. Výsledky
Při porovnání výsledků analytického a numerického modelu (Tab. 1) je vidět poměrně příznivá shoda. Využití pevnosti dřeva ve třech ze čtyř případů překračuje přípustné maximum.
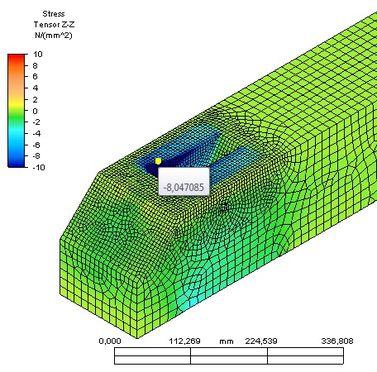
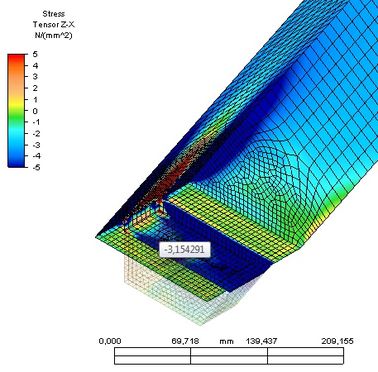
 Obr. 2 Vlevo normálové napětí ve směru osy z – tlak kolmo k vláknům, vpravo smykové napětí – usmyknutí zhlaví rovnoběžně s vlákny
Obr. 2 Vlevo normálové napětí ve směru osy z – tlak kolmo k vláknům, vpravo smykové napětí – usmyknutí zhlaví rovnoběžně s vlákny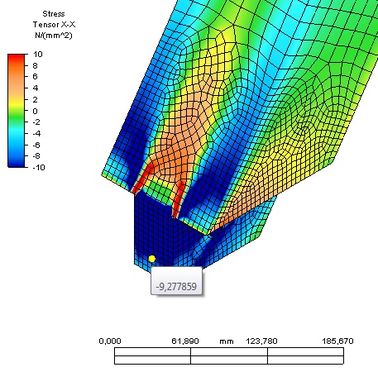
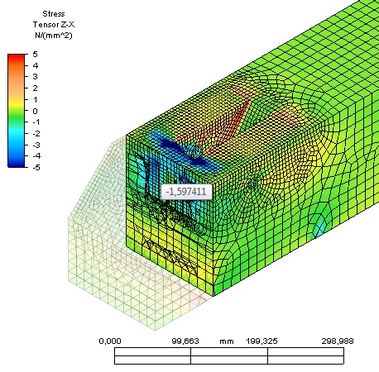
 Obr. 3 Vlevo normálové napětí ve směru osy x – tlak šikmo k vláknům, vpravo smykové napětí – usmyknutí čepu
Obr. 3 Vlevo normálové napětí ve směru osy x – tlak šikmo k vláknům, vpravo smykové napětí – usmyknutí čepu| Napětí | Analytické řešení [MPa] | Numerické řešení [MPa] | Využití přípustné charakteristické pevnosti [%] |
|---|---|---|---|
| σc,90,d | 7,65 | 8,05 | 306–322 |
| τv,d,zhlaví | 1,54 | 1,60 | 62–64 |
| σc,ß,d | 8,46 | 9,28 | 273–299 |
| τv,d,čep | 2,72 | 3,15 | 109–126 |
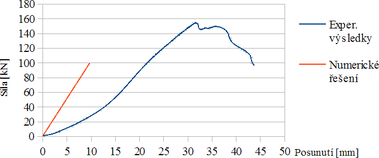
Na Grafu 1 je vykreslen posun na horním čele šikmého prvku – modrá čára a posun zjištěný z lineární analýzy – červená čára. Maximální hodnota posunu zjištěná laboratorně je u = 21,5 mm. Numerický model vyhodnotil tuto hodnotu cca o polovinu nižší: u = 9,7 mm. Důvod tohoto rozdílu je patrný z počátečního – nelineárního průběhu posunutí v laboratoři testovaného tesařského spoje.
5. Závěr
Při porovnání průběhu deformace tesařského spoje, zjištěného experimentálně a numericky, je patrný velký rozdíl. Ten je způsoben počátečním nepružným průběhem laboratorní zkoušky. Toto chování si lze vysvětlit pozvolným dosednutím spolupůsobících ploch čepu a dlabu tesařského spoje. Numerické výstupy řešení dávají vyšší hodnoty napětí, než jsou hodnoty zjištěné analytickým řešením. Z obrázků výsledků počítačové simulace jsou tyto vyšší hodnoty napětí jasně patrné a koncentrují se v oblasti dotykových ploch prvků tesařského spoje. Důvodem těchto vysokých hodnot může být typ kontaktu, který se mírně odchyluje od skutečného chování dosedajících ploch.
6. Poděkování
Tento článek byl zpracován za podpory grantu NAKI - DF12P01OVV037, jehož poskytovatelem je Ministerstvo kultury České republiky.
7. Literatura
- [1] POŽGAJ, Alexander a kolektiv. Štruktúra a vlastnosti dreva. Druhé vydání. Bratislava: Príroda, 1997. ISBN 80-07-00960-4.
- [2] KUKLÍK, Petr. Příručka 2: Navrhování dřevěných konstrukcí podle Eurokódu 5 [online]. Praha: Leonardo da Vinci Pilot Projects, 2008. [vid. 19. 10. 2012]. Dostupné z: http://fast10.vsb.cz/temtis/documents/handbook_2_CZ.pdf
- [3] VINAŘ, Jan a Václav KUFNER. Historické krovy: konstrukce a statika. Praha: Grada, 2004. ISBN 80-7169-575-0.
- [4] ČSN EN 1995-1-1 Eurokód 5: Navrhování dřevěných konstrukcí – Část 1-1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby. Praha: Český normalizační institut, prosinec 2006.
The subject of this paper is an analytical, numerical and experimental analysis of oblique middle mortise and tenon joint with short end of timber element and confrontation of detected stresses with characteristic strengths that is used in an assessment of carpentry joints stress according to Eurocode 5.