Porovnání stavu napjatosti v průřezu u ocelobetonové výztuže
Článek uvádí poznatky z porovnání stavů napjatosti v ocelobetonovém profilu obdélníkového průřezu. Stav napjatosti je stanoven podle dvou různých přístupů. První, založený na teorii spolupracujících prstenců, je rozvíjen na katedře geotechniky. Druhým, referenčním, je teorie železobetonu, aplikovaná v pozemním stavitelství. Porovnání stavů napjatosti slouží k posouzení, zda lze metodu spolupracujících prstenců aplikovat k řešení stavu napjatosti v tunelových ostěních z ocelobetonových profilů a k vymezení, za jakých podmínek. Ověření bylo provedeno na ocelobetonovém profilu s prutovým příhradovým nosníkem.
1. Úvod
Profil primárního ocelobetonového ostění podzemních děl a železobetonový profil stavebních prvků jsou po materiální a formální stránce téměř identické konstrukce. V obou případech jsou konstrukčním materiálem beton (stříkaný beton u obezdívek) a ocelové pruty. Nejčastějším tvarem profilu je obdélník. Oba typy konstrukce profilu se odlišují v technologii provádění a způsobu zatěžování. Železobetonové stavební prvky jsou nejdříve zhotoveny, posléze instalovány a zatěžovány. Ocelobetonová ostění podzemních děl jsou vždy prováděna na místě a již během jejich provádění jsou zatěžována. Dalším zásadním rozdílem je, že ocelobetonová ostění jsou prováděna etapovitě, protože technologie stříkaného betonu je limitována tloušťkou vrstvy, na kterou lze provést nástřik. Po uplynutí jisté doby, poté co předchozí vrstva stříkaného betonu utuhne a stane se samonosnou, se proces nástřiku opakuje, dokud tloušťka stříkaného betonu nedosáhne požadované velikosti. Dalším zásadním rozdílem je obloukovitý tvar konstrukce tunelového ostění. Zakřivení obloukové konstrukce ve vrcholu klenby, bocích a protiklenbě mají různé poloměry a podobně jsou různé i tloušťky nástřiku betonu. Konstrukce ostění je budována postupně. V prvních fázích je oblouková konstrukce zajišťující klenbu a boky neuzavřená. Teprve provedením protiklenby se konstrukce uzavírá a vytváří tuhý rám. Navrhování parametrů a posouzení únosnosti obloukové konstrukce provedené z ocelobetonu (stříkaný beton a ocelové pruty) v podmínkách určovaných výstavbou podzemního díla, které jsou charakterizovány etapovitostí provedení, obloukovitými konstrukcemi a časovou proměnlivostí geometrických a přetvárných parametrů ostění, vyžaduje metody, které jsou schopny uvedené okolnosti obsáhnout a exaktně kvantifikovat.
Teorie spolupracujících prstenců provádí materiálovou homogenizaci skutečného profilu ocelobetonového ostění, přičemž zůstává zachován tvar profilu, jeho výška a šířka. Materiálová homogenizace se týká pouze hodnot přetvárných parametrů materiálů – modulu pružnosti a Poissonova čísla – z nichž je profil konstruován. Jejím výsledkem je pro daný profil jediná hodnota modulu pružnosti. Tato hodnota je následně aplikována v dalších statických výpočtech k řešení vnitřních sil a deformací obloukové ocelobetonové konstrukce. Výsledkem procesu homogenizace jsou další proměnné, které umožňují přepočet stavu napětí v homogenizovaném profilu na stav napětí ve skutečných materiálech.
Článek je věnován porovnání výsledků stavu napjatosti, který je výsledkem výpočtů provedených dle teorie spolupracujících prstenců, se stavem napjatosti v profilu vypočítaném dle teorie železobetonu. Cílem srovnání je posoudit, do jaké míry a pro jaké podmínky lze stav napjatosti v profilu, stanovený dle teorie spolupracujících prstenců, považovat za objektivní.
2. Teorie spolupracujících prstenců
Cílem teorie spolupracujících prstenců je odvození jediné hodnoty modulu pružnosti, která bude reprezentovat strukturu a konstrukční materiály (stříkaný beton, ocel) profilu ostění. Vlastní řešení tohoto cíle vychází z analytického modelu pro výpočet napěťo-deformačního stavu ve vícevrstvém kruhovém prstenci, který byl formulován (BULYTCHTEV, 1982). Vnější zatížení na ostění, normálové i smykové, jsou rozpočtena na jednotlivé vrstvy – prstence, na které je ostění podle své struktury členěno. Tyto prstence mohou být homogenní, tvořeny jedním materiálem (beton), nebo nehomogenní, tvořeny dvěma materiály (beton a ocel; ocel a volný prostor). Rozpočet je uskutečněn pomocí tzv. přenosových koeficientů, které obecně plynou z podmínky spojitosti deformací na jednotlivých kontaktech mezi prstenci. Není zde zachována spojitost přenosu napětí na rozhraní dvou sousedních prstenců. Hodnota napětí na vnitřním okraji vnitřního prstence je rovna nule. Přenosové koeficienty jsou funkcemi tlouštěk a přetvárných charakteristik skutečných materiálů jednotlivých prstenců (Poissonovo číslo, modul pružnosti). Z h odnot přenosových koeficientů jsou určeny velikosti napětí na jednotlivých kontaktech mezi prstenci. Výpočetní postup pro stanovení jednotné hodnoty modulu pružnosti nehomogenního ostění se člení do dvou dílčích kroků:
- dílčí homogenizace materiálně nehomogenních prstenců (beton-ocel, ocel-volný prostor)
- globální homogenizace dílčích prstenců, která probíhá postupně, vždy na dvou sousedních prstencích.V prvním kroku jsou homogenizovány dva první prstence, vnitřní prstenec a jeho soused. Dále se postup opakuje, k nově vzniklému (ze dvou předchozích prstenců) je připojen následující dílčí prstenec. Postup se opakuje dokud nejsou všechny prstence sloučeny do jednoho celku.
Výsledkem homogenizace je jediná hodnota modulu pružnosti, reprezentující strukturu a konstrukční materiály profilu ostění a přenosové koeficienty napětí. Z přenosových koeficientů napětí jsou dále odvozeny přerozdělovací koeficienty, které slouží pro zpětný výpočet hodnot napětí v k rajních vláknech jednotlivých prstenců, homogenních i nehomogenních, ve skutečných materiálech, tj. v betonu a oceli. Celá teorie spolupracujících prstenců je podrobně uvedena v (ALDORF, J., HRUBEŠOVÁ, E., VOJTASÍK, K., ĎURIŠ, L., 2008).
3. Metoda o věření teorie spolupracujících prstenců
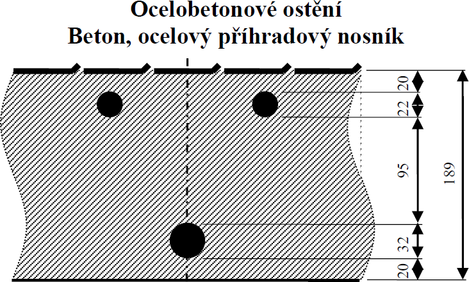
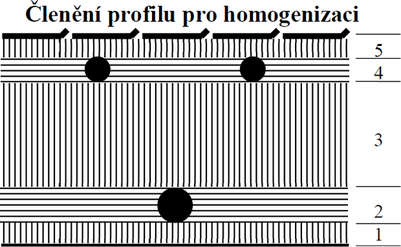
Ověření teorie spolupracujících prstenců je založeno na srovnání výsledků stavu napjatosti v profilu s referenčním stavem napjatosti, který je definován dle teorie železobetonu. Porovnání je provedeno pro typický profil ocelobetonového ostění, které má tloušťku 189 mm a je vyztužené příhradovým prutem ASTA 95 (obr. 1).
Vnitřní poloměr oblouku konstrukce ostění je 3,5 m. Šířka pásu ostění a rozteč umístění příhradových prutů v ostění jsou rovny jednomu metru. Překrytí ocelových prvků příhradového prutu stříkaným betonem činí 20 mm. Moduly pružnosti betonu a oceli jsou 20 000 MPa pro beton, 210 000 MPa pro ocel. Poissonovo číslo je pro oba materiály rovno 0,2 a stejná hodnota je požadována i zadána pro homogenizovaný profil. Programem HOMO, který je založen na teorii spolupracujících prstenců, jsou vypočteny modul pružnosti homogenizovaného profilu a přerozdělovací koeficienty k přepočtu napětí v materiálech v jednotlivých prstencích. Pro řešenou konstrukci profilu ostění hodnota homogenizovaného modulu pružnosti činí 22 000 MPa a hodnoty přerozdělovacích koeficientů pro jednotlivé prstence jsou uvedeny v tabulce č. 1. Z pohledu teorie železobetonu představuje ostění oboustranně vyztužený betonový profil obdélníkového tvaru, jehož rozměry jsou: výška h 189 mm; šířka 1000 mm. Stupeň vyztužení profilu je cca 1 %.
Stav napjatosti v betonovém, popřípadě železobetonovém profilu, je obecně určen velikostmi hodnot vnitřních sil, tj. normálovou silou a ohybovým momentem (uvažován je případ rovinného zatížení konstrukce ostění). V případě malé excentricity v profilu budou působit jen tlaková napětí s extrémními hodnotami, minimem a maximem v krajních vláknech profilu. Za podmínek velké výstřednosti v profilu budou působit současně jak tlaková, tak tahová napětí. Za této situace je nutno betonový profil vyztužit ocelovou výztuží na té části profilu, kde se očekávají tahová napětí. Možné je i vyztužení profilu na obou částech namáhaných jak tahovým, tak i tlakovým napětím. Prvky ocelové výztuže se umísťují ke krajním hranám profilu. Tloušťka překrytí ocelových prvků betonem je stanovena na 20 mm. Při současném tahovém a tlakovém namáhání stav napjatosti v profilu může být posuzován následujícími přístupy: betonový profil – s v yloučením tahu; betonový profil vyztužený ocelí – jednostranně vyztužený, nebo oboustranně vyztužený.
K ověření výsledků teorie spolupracujících prstenců byly aplikovány dva stavy napjatosti v profilu. První reprezentuje stav s malou excentricitou, druhý stav velkou excentricitu a oboustranně vyztužený profil.
| Varianta | Číslo prstence | Ehomo [MPa] | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||||
| 1 | beton | vnitřní poloměr | 0,91 | 0,81 | 1,02 | 0,91 | 1,45 | 22 000 |
| vnější poloměr | 0,91 | 0,81 | 1,02 | 0,91 | 1,45 | |||
| ocel | vnitřní poloměr | 9,54 | 9,46 | |||||
| vnější poloměr | 9,54 | 9,46 | ||||||
4. Výsledky
Výsledky výpočtů stavu napjatosti v profilu pro hodnoty vnitřních sil působících s malou a s velkou excentricitou jsou znázorněny graficky na obrázcích č. 2 (situace s malou excentricitou) a č. 3 (situace s velkou excentricitou).
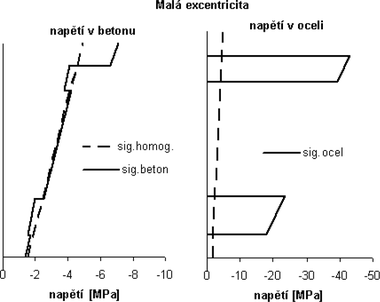
Obr. 2: Stav napjatosti v profilu ostění stanovený dle teorie spolupracujících prstenců – malá excentricita působících vnitřních sil
Za předpokladu malé excentricity působících vnitřních sil jsou hodnoty napjatosti v jednotlivých materiálech (betonu a oceli), stanovené prostřednictvím přerozdělovacích koeficientů (tabulka č. 1) z hodnot napjatosti v homogenizovaném profilu, v souladu se skutečností. Průběh napjatosti v b etonu napříč profilem není spojitý (sig.beton). Na úsecích, které odpovídají nehomogenním prstencům, dochází k skokové změně. Tato změna je dána nehomogenní strukturou prstence, tj. existencí dvou různých hodnot přetvárných parametrů (beton, ocel). Rovněž analogický, stupňovitý průběh lze očekávat i mezi dvěma homogenními prstenci, pokud tyto budou mít odlišné hodnoty přetvárných parametrů. Stupňovitý průběh je zákonitým projevem, který plyne z podmínky spojitosti deformací.
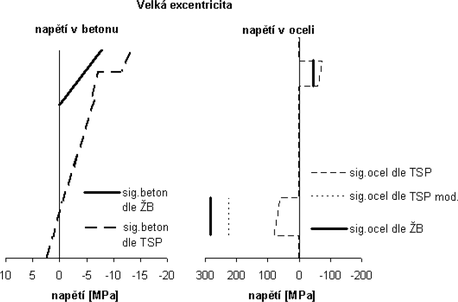
Obr. 3: Porovnání stavů napjatosti v profilu ostění stanovených dle teorie spolupracujících prstenců (TSP) a teorie železobetonu (ŽB) pro oboustranně vyztužený profil – velká excentricita působících vnitřních sil
Pro situace s velkou výstředností se hodnoty a průběh stavu napjatosti dle teorie spolupracujících prstenců plně neshodují s řešením dle teorie železobetonu. Přesto, jak je patrno z obr. č. 3, zde existuje obecná principiální shoda výsledků. Odlišnost výsledků dle teorie spolupracujících prstenců je daná podmínkami odvození této teorie. Hlavní rozdíl spočívá v okolnosti, že v teorii železobetonu je vyloučen beton z činnosti na té části profilu, kde dochází ke vzniku tahových napětí. Tato skutečnost je hlavní příčinou rozdílů, kterými jsou: různá poloha neutrální osy profilu a z toho plynoucí rozdílné délky úseku tlačené části profilu; odlišná maximální hodnota tlakového napětí v betonu v krajních vláknech profilu; výrazně odlišná hodnota tahového napětí v oceli v tažené časti profilu. Maximální hodnota tlakového napětí v betonu v krajních vláknech v případě teorie spolupracujících prstenců je vyšší oproti řešení dle teorie železobetonu. Nejvýznamnější rozdíl je u oceli v tažené části profilu. Tahové napětí v oceli dle teorie železobetonu je až šestinásobkem hodnoty plynoucí z teorie spolupracujících prstenců. Mají-li být výsledky stavu napjatosti stanovené dle teorie spolupracujících prstenců za podmínek velké excentricity aplikovány k posouzení únosnosti profilu, je potřeba metodiku výpočtu napětí upravit tak, aby byla respektována okolnost vyloučení tahových napětí v betonu a hodnota tahového napětí v betonu byla připočtena k stavu napětí v oceli. Na obrázku č. 3 je uvedena hodnota napětí v oceli v tažené části profilu (sig.ocel dle TSP mod), která byla stanovena dle výše navržené úpravy. Její velikost je součtem hodnoty tahového napětí, stanovené dle teorie spolupracujících prstenců (sig.ocel dle TSP), a hodnoty plynoucí z vyloučení tahu v betonu. Tato je stanovena z maximální hodnoty tahového napětí v betonu v krajních vláknech na tažené části profilu, určené dle teorie spolupracujících prstenců, a délky úseku, na kterém budou působit tahová napětí (dle teorie ŽB). I po této úpravě výpočtu stavu napětí v oceli na tažené části profilu je hodnota napětí v oceli menší, než je tomu v případě výpočtu dle teorie železobetonu. Nicméně došlo k výraznému snížení existujícícho rozdílu v napětí ocelového prvku.
5. Závěr
Dle teorie spolupracujících prstenců lze provádět výpočty stavu napjatosti v kompozitních typech profilů, u kterých se ve stavbě profilu kombinují různé materiály, které disponují jak tlakovou, tak i srovnatelnou tahovou pevností, to ale není případ ocelobetonových ostění.
V případě ocelobetonového ostění, kdy pevnost betonu v tahu je asi jednou desetinou pevnosti v tlaku, a za situace vnitřních sil působících s velkou excentricitou, kdy část profilu je namáhána tahem, nelze teorii spolupracujících prstenců přímo aplikovat. Zpětný přepočet stavu napětí do betonu a oceli je založen na přerozdělovacích koeficientech, kterými jsou přenásobeny hodnoty napětí. Samotná teorie spolupracujících prstenců pomíjí skutečnost, že na tažené části profilu jsou v betonu vyloučena tahová napětí a jejich hodnota je připočítaná k tahovému napětí v ocelových prvcích. V tomto smyslu je nutné zpětný výpočet napjatosti pro taženou části profilu ostění modifikovat, aby byla zohledněna i tato podstatná okolnost.
Uvedený poznatek, omezující platnosti výsledků výpočtu stavu napjatosti v ocelobetonovém profilu, nezpochybňuje tuto teorii, která je zaměřena v první řadě na stanovení reprezentativních přetvárných parametrů materiálově kombinovaných ostění. S respektováním výše uvedených poznatků mohou být její výsledky použity i pro hodnocení únosnosti profilů namáhaných vnitřními silami, působících s velkou excentricitou.
Poděkování
Příspěvek byl realizován za finančního přispění Grantové agentury ČR, projekt 103/09/1438 Výzkum pevnostních a přetvárných vlastností ostění ze stříkaného betonu vyztužených tuhými ocelovými prvky.
Úvodní ilustrační snímek pořídil při instalaci ocelobetonového ostění doc. Karel Vojtasík. Snímek zachycuje část boku díla s dokončeným a s aktuálně prováděným úsekem podzemního díla, které je zajišťováno ocelobetonovým ostěním, v poslední instalační operaci, během zastříkávání ocelových konstrukční prvků, tj. ocelového příhradového prutového rámu a ocelové mřížoviny, která zajišťuje - zapažuje plochu mezi dvěma sousedními rámy.
Literatura
- BULYTCHEV, N. C. Mechanika podzemnych sooruženij. Moskva: NEDRA, 1982. 270 pp.
- ALDORF, J., HRUBEŠOVÁ, E., VOJTASÍK, K., ĎURIŠ, L. Alternativní způsob stanovení tuhosti betonového ostění vyztuženého válcovými prvky. Sborník 3. konference Beton v podzemních a základových konstrukcích. Praha : CBS Servis, s.r.o., 2008, pp. 119–124. ISBN 978-80-87158-05-0.
The paper exposes knowledge referring a correspondence of stress states in the cross-section of steel concrete lining. The two different theories size the stress states. The first a theory of cooperating rings is pursued at department of geotechnics. The second referential is a reinforced concrete theory in use at building construction habitually. The correspondence targets the evaluation of suitability and the working condition of a cooperating rings theory to state the stress in the cross-section of steel concrete lining. An investigation was work out on a steel concrete section having been endorsing by lattice girder.