Analýza spojenia medzi doskou a stĺpom v súvislosti s aplikáciou CSCT
Príspevok sa zaoberá experimentálnou a nelineárnou analýzou spojenia medzi doskou a stĺpom v súvislosti s aplikáciou Teórie kritickej šmykovej trhliny (CSCT). Model CSCT je mechanický model, kde sa šmyková sila prenášaná betónom v šmykovej trhline môže určiť zohľadnením drsnosti a otvorenia kritickej šmykovej trhliny. Pre aplikáciu CSCT modelu je potrebné odhadnúť odozvu zaťaženia na pootočenie dosky. Doskové pootočenia boli vypočítané na základe nameraných deformácií bodov za vzniknutou kritickou šmykovou trhlinou. Predmetom tohto výskumu boli fragmenty bezprievlakovej dosky s hrúbkou 0,2 m, podopretej vnútorným stĺpom s obdĺžnikovým prierezom. Cieľom bolo vytvoriť numerický nelineárny model v programe Atena, ktorý zodpovedá reálnemu správaniu dosky počas zaťažovania až do následného kolapsu a taktiež overenie výsledkov získaných experimentálnym výskumom.
Úvod
Pretlačenie lokálne podopretých dosiek je stále veľmi aktuálnou a diskutovanou témou v oblasti posudzovania nosných konštrukcií budov. Pretlačenie stropných dosiek podopretých stĺpom s obdĺžnikovým prierezom, kde predpokladáme nerovnomerné rozloženie šmykových síl, bolo skúmané v mnohých vedeckovýskumných tímoch u nás i v zahraničí.
Kolaps bezprievlakových dosiek spôsobený dosiahnutím šmykovej odolnosti je jedným z najnebezpečnejších typov zlyhania kvôli svojmu krehkému charakteru. Prvé modely na určenie príčiny tohto javu sa vyvinuli od 60. rokov minulého storočia. Vychádzali z rôznych princípov, napríklad z modelov založených na mechanizme zlyhania (Kinnunen a Nylander) [1], z teórie plasticity (Braestrup-Nielsen) [2] alebo z modelov založených na ohybovej kapacite (Moe) [3].
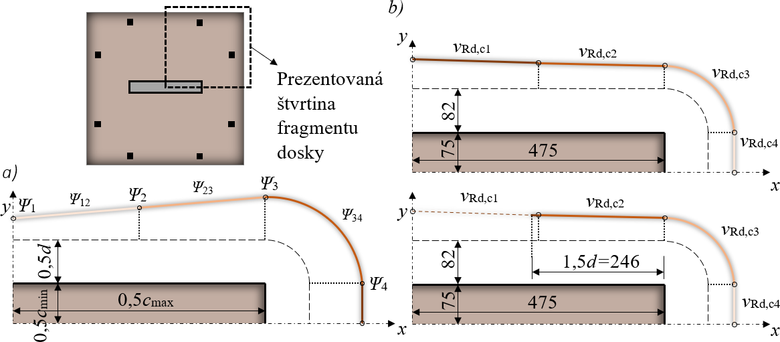
V súčasnosti existuje mnoho prístupov a modelov vyvinutých na stanovenie šmykovej odolnosti bezprievlakových dosiek. Jednou z nich je Teória kritickej šmykovej trhliny navrhnutá Muttonim a Schwartzom [4] v roku 1991, ktorá sa neskôr stala aj modelom aplikovaným v Model Code 2010 [5]. Rovnako ako model vyvinutý Kinnunenom a Nylanderom, aj CSCT dáva do súvislosti šmykovú odolnosť s pootočeniami dosky. Muttoni a Schwartz [4] predpokladali, že šírka tejto kritickej šmykovej trhliny je úmerná pootočeniu dosky ψ a účinnej výšky dosky d, tak ako to zobrazuje Obr. 1.
Predmetom tejto analýzy je fragment bezprievlakovej dosky podopretej obdĺžnikovým stĺpom s rozmermi 0,95 m × 0,15 m. Šmyková odolnosť dosiek podopretých obdĺžnikovým stĺpom je nižšia ako odolnosť dosiek podopretých štvorcovým stĺpom s približne rovnakou dĺžkou základného kontrolného obvodu. Tento jav je spôsobený skutočnosťou, že vzťahy na výpočet šmykovej odolnosti zahŕňajú empirické faktory, ktoré zohľadňujú iba geometriu podpery, ale nezohľadňujú zdeformovaný tvar dosky.
Critical Shear Crack Theory – CSCT
CSCT zohľadňuje mnoho faktorov pri posúdení šmykovej odolnosti lokálne podopretých dosiek, ktoré sa v súčasnosti platnom návrhovom modeli Eurocode 2 (EC2) [X] nevyskytujú. Táto teória predpokladá, že šmyková kapacita spojenia doska-stĺp sa znižuje v dôsledku zvýšenia rotácie dosky ψ a súvisiaceho otvárania kritickej šmykovej trhliny. Predpokladá sa, že množstvo šmykového napätia, ktoré je možné prenášať cez kritickú šmykovú trhlinu, závisí od drsnosti trhliny, ktorá sa odhaduje ako funkcia maximálnej veľkosti kameniva dg a pevnosti betónu v ťahu. Vzťah medzi šmykovou odolnosťou a pootočením dosky za kritickou šmykovou trhlinou je vyjadrený vzťahom (1).
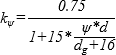 (2)
(2)
kde je
- kψ
- parameter zohľadňujúci pootočenie dosky vypočítaný podľa (2),
- γC
- parciálny súčiniteľ spoľahlivosti [–], pre túto analýzu bol použitý γC = 1,0,
- fck
- charakteristická pevnosť betónu v tlaku [MPa],
- b0
- dĺžka základného kontrolného obvodu vo vzdialenosti dv /2 od líca podpery
b0 = 2(c1 + c2) + 2π (d/2) [mm], - dv
- účinná výška dosky v šmyku [mm],
- ψ
- doskové pootočenie [–],
- d
- účinná výška dosky, priemerná hodnota účinnej výšky v smere x a v smere y [mm],
- dg
- maximálne zrno kameniva [mm].
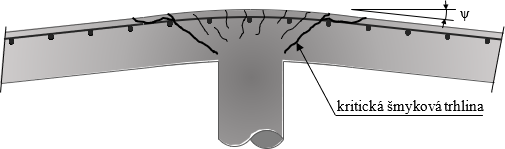
Obr. 1 Vznik kritickej šmykovej trhliny a s ňou súvisiace pootočenie dosky
Pre použitie CSCT metódy je potrebné stanoviť pootočenie bezprievlakovej dosky za kritickou šmykovou trhlinou. Pri vyhodnocovaní výsledkov experimentálnych testov je možné rotáciu priamo odmerať alebo ju možno vypočítať na základe nameraných deformácií za predpokladu deformácie dosky v tvare kužeľa okolo líca stĺpa (Obr. 1). Pri návrhu konštrukcií je možné závislosť medzi zaťažením a rotáciou odhadnúť pomocou nelineárnej analýzy alebo aplikovaním zjednodušených vzťahov pre výpočet.
Experimentálny program
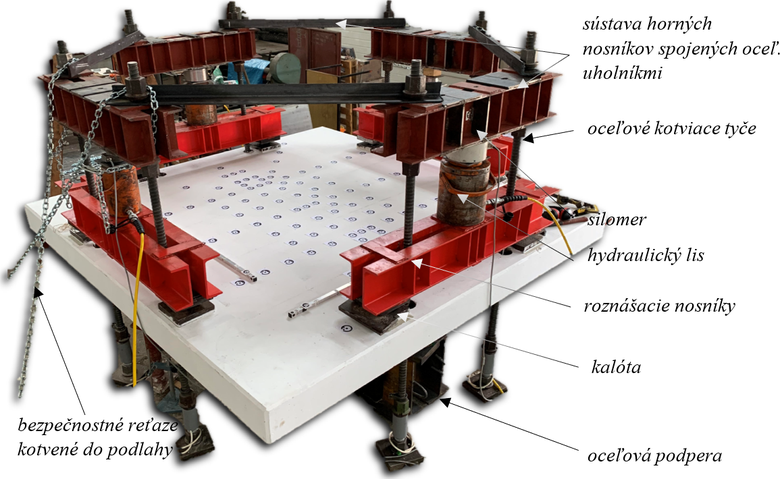
Experimentálny program zahŕňa súbor štyroch zaťažovacích skúšok fragmentu bezprievlakovej dosky podopretej vnútorným stĺpom. Skúšobná vzorka bola osadená na oceľovú podperu, pričom sa pomocou ôsmich oceľových tyčí priemeru Ø = 42 mm ukotvila do podlahy laboratória. Zaťažovanie vzoriek bolo realizované pomocou štvorice lisov a sústav nosníkov rozmiestnených po obvode dosky. Dvojice oceľových nosníkov boli rozopierané lismi umiestnenými v strede ich rozpätia, pričom sila bola do dosky vnášaná vždy v dvoch bodoch so vzájomnou vzdialenosťou 1 m. Spodné dvojice nosníkov boli podložené oceľovými kalótami, aby sa tak zabezpečilo kĺbové uloženie rámu a dosky. Horná sústava nosníkov bola diagonálne prepojená oceľovými uholníkmi, pričom dvojice nosníkov rovnobežných s dlhšou stranou stĺpa boli prichytené podlahu laboratória oceľovými reťazami.
Experimentálne testy sa líšili rôznym spôsobom zaťažovania jednotlivých vzoriek. Vzorka S2-1 bola zaťažovaná rovnomerne okolo celého obvodu v podobe ôsmych sústredených síl. Vzorka S2-2 bola zaťažovaná v pomere 2x/y (dve tretiny celkového zaťaženia boli aplikované v smere osi x, zvyšná tretina v smere y). Opačný prípad predstavovala vzorka S2-3, na ktorú bolo zaťaženie aplikované v pomere x/2y. Pri poslednej vzorke S2-4 bolo cieľom takmer jednostranné zaťažovanie zo smeru x; (9x/y), ktoré predstavuje najhorší prípad namáhania z pohľadu problematiky pretlačenia.
Experimentálne vzorky
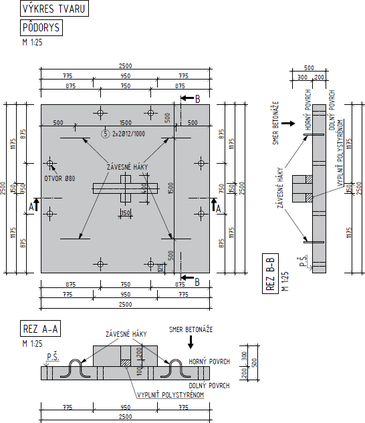
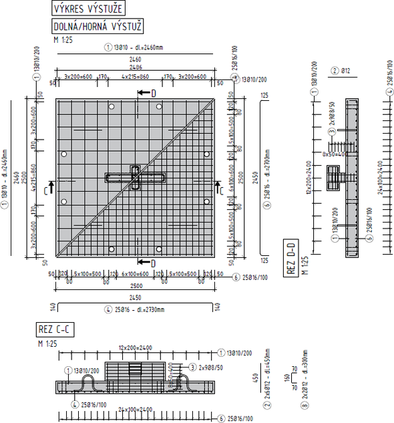
Experimentálne vzorky majú štvorcový pôdorys s rozmermi 2,5 × 2,5 m a hrúbku 0,2 m. Pôdorysné rozmery vzoriek boli stanovené s ohľadom na laboratórne podmienky (raster otvorov v podlahe laboratória 0,75 × 0,75 m, v ktorých budú upevnené oceľové tyče kotviace skúšobnú vzorku). Vzhľadom na vzdialenosť tyčí od osi stĺpa, t.j. poloha nulových radiálnych ohybových momentov, vzorka zodpovedá reálnej konštrukcii s rozpätím 5,1 m v oboch smeroch prislúchajúcich polí. Vzorky boli podopreté výrazne obdĺžnikovým stĺpom s rozmermi priečneho rezu 0,15 m × 0,95 m. Všetky vzorky boli rovnako vystužené viazanou výstužou z ocele triedy B500B, pri hornom povrchu prútmi s Ø = 16 mm rozmiestnených rovnomerne po 100 mm v oboch smeroch a pri dolnom povrchu prútmi s Ø = 10 mm po 200 mm. Krytie hornej výstuže bolo cnom = 30 mm. Vzorky neboli vystužené šmykovou výstužou.
Nelineárna analýza (NLFEA)
Na nelineárne výpočty bol v tejto analýze použitý program ATENA. Kalibrácia modelov bola založená na poznatkoch z predošlých experimentov podobného charakteru [7] realizovaných v Centrálnych laboratóriách Slovenskej technickej univerzite v Bratislave.
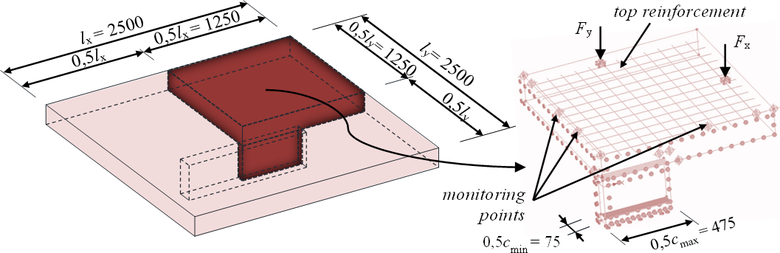
Vzhľadom na časovú náročnosť nelineárnych výpočtov je vhodné využiť symetriu modelovaných vzoriek. Vďaka tomuto faktu bolo možné namodelovať len štvrtinu celkovej vzorky, pričom sa použili okrajové podmienky zabezpečujúce jej symetrické správanie.
Podľa odporúčaní [6] sa zvolilo vhodné delenie siete 3D elementov so stranou kubického elementu a = 40 mm. Použitie „3D brick“ siete sa taktiež odporúča na dosiahnutie presnejších výsledkov. Vzorka bola podopretá plošne cez oceľovú podložku s hr. 50 mm umiestnenou pod fragmentom stĺpa. Vzorky boli zaťažované pomocou dvojice síl umiestnených v miestach oceľových kalót. Sily boli do dosky vnášané cez makroelementy reprezentujúce oceľové platničky (Obr. 4). Program Atena pracuje na kumulatívnom spôsobe zaťažovania, a teda v každom kroku bola pripočítaná sila, ktorá mohla byť korigovaná zadaním koeficientu kumulácie pri každom zaťažovacom kroku. Pomocou použitia tohto koeficientu mohli byť pri vyšších zaťaženiach jednotlivé zaťažovacie kroky zjemnené, aby sa dosiahla čo najpresnejšia hodnota celkovej sily pri zlyhaní. Základným zaťažovacím krokom bola sila o hodnote 12,5 kN (50 kN na celú vzorku), pričom v prvom kroku bola k sile pripočítaná aj vlastná tiaž vzorky.
Výsledky analýzy
Na základe kalibrácie parametrov výpočtového modelu a dosiahnutia dobrej zhody medzi experimentálnymi výsledkami s výsledkami z NLFEA sa numerické modely použili na zistenie pootočení po dĺžke kontrolného obvodu, ktoré sú funkciou napätia vo výstuži.
Podľa CSCT je šmyková odolnosť funkciou pootočenia dosky. V prípade podopretia dosky obdĺžnikovým stĺpom nie sú pootočenia dosky konštantné po obvode stĺpa. Šmyková odolnosť jednotlivých vzoriek bola vypočítaná na základe výsledného pootočenia ψ získaného tromi spôsobmi:
- integráciou šmykových odolností jednotlivých častí plného kontrolného obvodu s použitím príslušných pootočení ψi
- integráciou šmykových odolností jednotlivých častí redukovaného kontrolného obvodu s použitím príslušných pootočení ψi
- s uvážením maximálneho pootočenia vo výpočte šmykovej odolnosti dosky ψ = ψmax na plnom kontrolnom obvode.
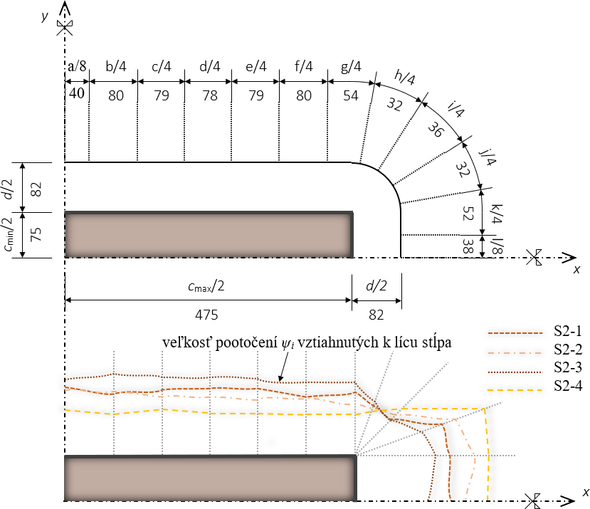
Kontrolný obvod bol rozdelený na niekoľko segmentov, na ktorých bolo uvažované konštantné pootočenie (Obr. 5). Tieto pootočenia boli merané vo vzdialenosti 2d (≈ 330 mm) od líca stĺpa. Na základe pootočení bola vypočítaná šmyková odolnosť danej časti kontrolného obvodu. Výsledné hodnoty pootočení a k nim prislúchajúce odolnosti sú zhrnuté v Tab. 1 až Tab. 4.
| Segment | Pootočenie | b0,i | VR,c (b0) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S2-1 | S2-2 | S2-3 | S2-4 | S2-1 | S2-2 | S2-3 | S2-4 | ||
| [mRad] | [m] | [kN] | |||||||
| a | 11,21 | 10,61 | 12,37 | 7,40 | 0,160 | 57,7 | 62,6 | 57,3 | 66,2 |
| b | 10,10 | 10,54 | 13,35 | 6,68 | 0,320 | 121,0 | 125,5 | 110,3 | 137,3 |
| c | 10,83 | 9,60 | 12,79 | 7,46 | 0,315 | 115,5 | 128,7 | 111,0 | 130,0 |
| d | 11,02 | 9,58 | 12,82 | 6,91 | 0,310 | 112,8 | 126,7 | 109,1 | 131,5 |
| e | 11,11 | 9,13 | 12,65 | 6,87 | 0,315 | 114,2 | 131,4 | 111,6 | 133,9 |
| f | 9,59 | 9,40 | 12,00 | 6,70 | 0,320 | 123,7 | 131,9 | 116,3 | 137,2 |
| g | 10,40 | 8,36 | 12,05 | 6,70 | 0,217 | 81,1 | 93,9 | 78,7 | 93,1 |
| h | 8,73 | 8,21 | 9,43 | 7,73 | 0,129 | 51,8 | 56,1 | 52,2 | 52,5 |
| i | 8,26 | 9,40 | 8,10 | 10,92 | 0,143 | 58,8 | 59,0 | 61,6 | 50,5 |
| j | 15,13 | 17,45 | 11,38 | 22,49 | 0,129 | 40,0 | 39,1 | 48,0 | 30,7 |
| k | 15,52 | 19,53 | 13,10 | 21,82 | 0,207 | 63,5 | 58,8 | 72,1 | 50,3 |
| l | 15,71 | 17,99 | 11,78 | 21,57 | 0,150 | 45,7 | 44,7 | 55,0 | 36,7 |
| Súčet | 2,715 | 985,6 | 1058,2 | 983,1 | 1049,8 | ||||
| Segment | Pootočenie | b0,i | VR,c (b0,red) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S2-1 | S2-2 | S2-3 | S2-4 | S2-1 | S2-2 | S2-3 | S2-4 | ||
| [mRad] | [m] | [kN] | |||||||
| a | 11,21 | 10,61 | 12,37 | 7,40 | 0,000 | – | – | – | – |
| b | 10,10 | 10,54 | 13,35 | 6,68 | 0,000 | – | – | – | – |
| c | 10,83 | 9,60 | 12,79 | 7,46 | 0,000 | – | – | – | – |
| d | 11,02 | 9,58 | 12,82 | 6,91 | 0,189 | 68,7 | 77,3 | 66,5 | 80,1 |
| e | 11,11 | 9,13 | 12,65 | 6,87 | 0,315 | 114,2 | 131,4 | 111,6 | 133,9 |
| f | 9,59 | 9,40 | 12,00 | 6,70 | 0,320 | 123,7 | 131,9 | 116,3 | 137,2 |
| g | 10,40 | 8,36 | 12,05 | 6,70 | 0,217 | 81,1 | 93,9 | 78,7 | 93,1 |
| h | 8,73 | 8,21 | 9,43 | 7,73 | 0,129 | 51,8 | 56,1 | 52,2 | 52,5 |
| i | 8,26 | 9,40 | 8,10 | 10,92 | 0,143 | 58,8 | 59,0 | 61,6 | 50,5 |
| j | 15,13 | 17,45 | 11,38 | 22,49 | 0,129 | 40,0 | 39,1 | 48,0 | 30,7 |
| k | 15,52 | 19,53 | 13,10 | 21,82 | 0,207 | 63,5 | 58,8 | 72,1 | 50,3 |
| l | 15,71 | 17,99 | 11,78 | 21,57 | 0,150 | 45,7 | 44,7 | 55,0 | 36,7 |
| Súčet | 1,799 | 647,4 | 692,0 | 662,0 | 664,9 | ||||
| Segment | Pootočenie | b0 | VR,c (b0 + ψmax) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S2-1 | S2-2 | S2-3 | S2-4 | S2-1 | S2-2 | S2-3 | S2-4 | ||
| [mRad] | [m] | [kN] | |||||||
| a–l | 15,71 | 19,53 | 13,10 | 22,49 | 2,715 | 826,3 | 770,6 | 945,1 | 646,2 |
| Vzorka | VTEST | VATENA | Vψ (b0) | Vψ (b0,red) | Vψ,max | VTEST / Vcalc | VATENA / Vcalc | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Vψ | Vψ (b0,red) | Vψ,max | Vψ | Vψ (b0,red) | Vψ,max | ||||||
| S2-1 | 821 | 831 | 985,6 | 647,4 | 826,3 | 0,83 | 1,27 | 0,99 | 0,84 | 1,28 | 1,01 |
| S2-2 | 884 | 836 | 1058,2 | 692,0 | 770,6 | 0,84 | 1,28 | 1,15 | 0,79 | 1,21 | 1,08 |
| S2-3 | 949 | 919 | 983,1 | 662,0 | 945,1 | 0,97 | 1,43 | 1,00 | 0,93 | 1,39 | 0,97 |
| S2-4 | 796 | 756 | 1049,8 | 664,9 | 646,2 | 0,76 | 1,20 | 1,23 | 0,72 | 1,14 | 1,17 |
| Priemer | 0,85 | 1,29 | 1,09 | 0,82 | 1,25 | 1,06 | |||||
Šmyková odolnosť bola na základe pootočení získaných z nelineárnej analýzy vypočítaná s kritériom porušenia podľa Teórie kritickej šmykovej trhliny. Výpočet šmykovej odolnosti metódou integrácie pootočení pozdĺž neredukovanej dĺžky kontrolného obvodu sa javí na strane nebezpečnej, nakoľko spoľahlivosť sa pohybuje v rozmedzí 0,76 až 0,97. Naopak najkonzervatívnejšia metóda výpočtu je aplikácia vypočítaných pootočení na jednotlivých segmentoch na redukovanej dĺžke kontrolného obvodu. Výrazný nárast spoľahlivosti je spôsobený vylúčením časti kontrolného obvodu, ktorá sa najviac podieľa na celkovej šmykovej odolnosti dosky. Podľa CSCT modelu bola dosiahnutá najlepšia zhoda s experimentálnymi výsledkami pri uvážení výpočtu šmykovej odolnosti s maximálnym pootočením ψmax aplikovaným na celú dĺžku kontrolného obvodu. Spoľahlivosť modelu dosiahla 0,99 až 1,23 v závislosti od spôsobu zaťažovania vzorky.
Vypočítaná šmyková odolnosť bola porovnaná nielen s experimentálne nameranými výsledkami, ale aj s hodnotami šmykovej odolnosti získanými numerickou nelineárnou analýzou. Toto porovnanie umožnilo vylúčiť chyby v meraní či materiálové nezrovnalosti. Rozdiel medzi pomerom VTEST / Vcalc a VATENA / Vcalc predstavuje len 3–4 %, čím možno potvrdiť správnosť nameraných výsledkov.
Záver
Predmetom tohto článku bola aplikácia CSCT metódy na výsledky numerického nelineárneho modelu a na experimentálne získané výsledky. Na základe tejto analýzy boli vyvodené nasledovné závery:
- Podľa CSCT teórie má významný podiel na celkovej šmykovej odolnosti dosky práve časť kontrolného obvodu, ktorá sa z výpočtu pri uvážení redukcie jeho dĺžky vynecháva. Takto vypočítaná šmyková odolnosť dosiek dosahuje pomerne konzervatívne výsledky s mierou spoľahlivosti 1,2 až 1,43 v závislosti od spôsobu zaťažovania.
- Najlepšia zhoda v šmykovej odolnosti vzoriek s experimentálne nameranými výsledkami bola preukázaná v aplikácii CSCT modelu s uvážením maximálneho pootočenia po celej dĺžke kontrolného obvodu.
- Vzhľadom na nízky percentuálny rozdiel (3–4 %) medzi pomerom VTEST / Vcalc a VATENA / Vcalc sa potvrdila správnosť nameraných experimentálnych výsledkov.
Poďakovanie
Táto práca vznikla s podporou výskumného projektu VEGA č. VEGA 1/0310/22 „Špecifické aspekty vplývajúce na šmykovú odolnosť železobetónových nosných prvkov pri koncentrovanom namáhaní“.
Literatúra
- Kinnunen, S., Nylander, H. (1960) Punching of concrete slabs without shear reinforcement, In Transaction No. 158, Royal Institute of Technology, Stockholm.
- Braestrup, M. W., Nielsen, M. P. (1976) Axisymmetric Punching of Plain and Reinforced Concrete, In Report No. R75, Denmark.
- Moe, J., (1961) Shearing Strength of Reinforced Concrete Slabs and Footings under Concentrated Loads, In Bulletin D47, Chicago.
- Muttoni, A., Schwartz, J. (1991) Behaviour of Beams and Punching in Slabs without Shear Reinforcement, In IABSE Colloquium Vol. 62, Zurich, Switzerland, 703-708.
- Fédération Internationale du Béton (fib) (2012) Model Code 2010 - Final draft, Fédération Internationale du Béton Bulletin 65, Lausanne, Switzerland, Vol 2.
- Červenka, V., Jendele, L., & Červenka, J. (2018). ATENA program documentation, Part 1, Theory. Prague: s.n.
- Augustin, T., Fillo, L., Halvonik, J. (2019). Punching resistance of slab-column connections with openings, in Structural Concrete.