Hodnotenie úrovne predpätia v konštrukcii s využitím teórie podmienenej pravdepodobnosti
Hodnotenie spoľahlivosti a zostatkovej životnosti predpätých konštrukcií a mostov, sa hlavne vo svetle niektorých nedávnych mimoriadnych udalostí, stávajú čoraz dôležitejšími. Problematické predpäté mostné konštrukcie prvej generácie sú v prevádzke už viac ako šesťdesiat rokov, a teda znalosť aktuálneho stavu ich predpätia je základným vstupom pre každý statický prepočet. Táto skutočnosť vedie k potrebe overenia rôznych metód, ktoré umožnia určiť aktuálnu hodnotu predpínacej sily. Príspevok nadväzuje na prácu tímu, ktorý sa na Katedre stavebných konštrukcií a mostov Stavebnej fakulty v Žiline, už dlhodobo venuje výskumu spoľahlivosti predpätých konštrukcií. Zaoberá sa konkrétne analýzou predpätia s využitím nepriamych, analyticko-experimentálnych metód, akou sú aj metódy uvoľnenia napätí (rezová metóda/Saw-cut Method). Táto metóda bola testovaná na sérii meraní na vopred predpätých železničných podvaloch. Experimentálne výsledky boli komparované s teoretickým výpočtom a následne platnosť výsledkov objektivizovaná využitím konceptu podmienenej pravdepodobnosti – Bayes model.
1. Úvod
Vo viacerých európskych krajinách bola značná časť infraštruktúry vybudovaná v povojnovom období. Skúsenosti s havarijnými stavmi niekoľkých mostov z nedávnej minulosti ukazujú, že viaceré mosty, hlavne predpäté, sa blížia k hranici svojej životnosti už po približne šesťdesiatich rokoch prevádzky. Celkový stav existujúcich mostov odráža nielen úroveň rozvoja spoločnosti, v ktorej boli postavené, ale aj kultúrnu a ekonomickú silu súčasnej generácie, keďže odzrkadľuje starostlivosť o tieto zdedené inžinierske stavby. V prípade týchto mostov má predpätie rozhodujúci vplyv na ich celkovú statickú funkčnosť a spoľahlivosť, ktorá ako sa ukazuje, v čase významne klesá. Nie je to len dôsledok reologických vplyvov betónu, ale aj už od počiatku nevhodný stav ochrany kotvenia, ako aj predpínacích jednotiek, ktoré následne korodujú v kombinácii so značným preťažovaním mostov a ich nedostatočnou údržbou [1]. V súčasnosti je k dispozícii niekoľko technicky akceptovateľných metód pre stanovenie aktuálnej úrovne predpätia [1, 2]. Tieto metódy možno rozdeliť do dvoch hlavných skupín – priame a nepriame metódy. Priame metódy vedú k stanoveniu predpínacej sily priamo z merania pomerných pretvorení alebo napätosti predpínacej jednotky. Aplikácia týchto metód v existujúcich konštrukciách je však veľmi obmedzená presnosťou a technickými možnosťami merania. Preto sa ako najvhodnejšia alternatíva javí aplikácia semi-deštruktívnych nepriamych metód [2, 3]. Nepriame metódy zahŕňajú napríklad metódy založené na systéme uvoľnenia napätia v betónovom prvku. Ide predovšetkým o rezovú metódu (Saw-cut Method) a vŕtaciu metódu (Drilling Method).
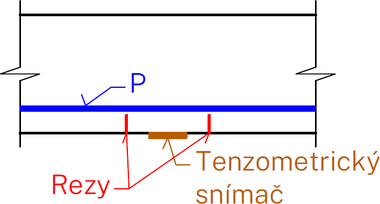
Rezová metóda (Obr. 1) funguje na princípe aplikácie zvyčajne dvojice rezov, ktoré vyvodia uvoľnenie normálového napätia v priereze bez trhlín. Týmto spôsobom vytvoríme „izolovaný betónový blok“. Zmenu pomerných pretvorení zaznamenáme v priľahlých miestach použitím tenzometrických snímačov. Betónový blok je možné považovať za úplne izolovaný vtedy, keď narastajúca hĺbka rezu už viac nespôsobuje výraznú zmenu pomerných pretvorení v priľahlých miestach. Ďalej je možné spomenúť metódu odozvy konštrukcie na vonkajšie zaťaženie (Structural Response Method) – analýza vzniku/znovuotvorenia trhliny, sledovanie pomerných pretvorení, deformácií [2, 3].
Tento príspevok je zameraný na testovanie spoľahlivosti rezovej metódy v laboratórnych podmienkach na vopred predpätých prvkoch, aby sa v maximálne možnej miere eliminovali neistoty merania vyplývajúce z aplikácie metódy in-situ. Z toho dôvodu bola zvolená séria troch kusov predpätých betónových podvalov typu B70 W-49 G, ktorá bola skúšaná približne po 1 roku od ich výroby, Obr. 2. Ich dĺžka bola 2600 mm, minimálna výška v strednej časti 175 mm a maximálna výška 234 mm. Šírka priečneho rezu bola premenná od 220 do 300 mm pri spodnej hrane a od 145,9 do 171 mm pri hornej hrane. Hlavné rozmery je možné vidieť na Obr. 3. Výrobca deklaroval, že podvaly boli vyrobené z pevnostnej triedy betónu C50/60, pričom ich hmotnosť mala mať hodnotu 288 kg. Predpätie bolo zaistené celkovo ôsmimi hladkými predpínacími drôtmi s priemerom 7 mm. V čase experimentu mali vzorky približne jeden rok. Vďaka skutočnosti, že ide prefabrikované vzorky vysokej kvality, dalo sa očakávať, že povrch, na ktorom budú nainštalované lepené odporové fóliové tenzometre bude umožňovať bezproblémové meranie zmeny pomerných pretvorení po aplikácii rezov.
2. Opis experimentálnych meraní
Ako už názov použitej metódy naznačuje, iniciácia uvoľnenia normálových napätí bola realizovaná vytvorením priečnych rezov cez podval. Rezy boli vedené na zvolených miestach na priamej ploche v strede podvalov, tak aby vznikli na každom podvale po dva izolované betónové bloky, na ktorých sa sledovala zmena pomerných pretvorení pomocou nalepených odporových tenzometrov typu HBM LY41-50/120. Vo všeobecnosti je možné, v prípade predpätého prvku bez trhlín, z uvoľnených hodnôt normálového napätia (Δσc,i) odvodiť veľkosť predpínacej sily v danom čase Pm,t = Presidual podľa vzťahu (1),
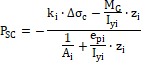 (1)
(1)
kde je
- ki
- faktor vyjadrujúci mieru uvoľneného normálového napätia,
- ∆σc
- uvoľnené normálové napätie,
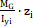
- príspevok normálového napätia od stáleho zaťaženia,
- Ai ; epi ; Iyi ; zi
- parametre skúmaného ideálneho prierezu.
![Obr. 4 – Závislosť medzi hĺbkou rezu (h), osovou vzdialenosťou medzi rezmi (d) a percentuálnym uvoľnením napätia [%]](/docu/clanky/0252/025211o12.png)
Obr. 4 – Závislosť medzi hĺbkou rezu (h), osovou vzdialenosťou medzi rezmi (d) a percentuálnym uvoľnením napätia [%]
Dva hlavné faktory, ktoré ovplyvňujú veľkosť uvoľneného normálového napätia, sú hĺbka a osová vzdialenosť vykonávaných rezov. V našom prípade boli aplikované rezy postupne až do 30 mm hĺbky. V prípadoch, kedy nie je možné docieliť plnú izoláciu normálového napätia (100 %), môžeme výhodne využiť numerické simulácie. Medzi prípady obmedzujúce maximálnu hĺbku rezov patrí napr. malé krytie výstuže v prípade starších konštrukcií – cieľom je neprerezať betonársku a predpínaciu výstuž. Faktor vyjadrujúci mieru uvoľneného napätia ki bol odvodený a popísaný v [4] a závery parametrickej štúdie rezovej metódy sú odprezentované na Obr. 4.
V rámci experimentu boli vykonané skúšky materiálov vzoriek pre dôsledné vyhodnotenie meraní. Znalosť materiálových charakteristík (predovšetkým modulu pružnosti betónu) je kľúčová pre správne určenie reziduálnej hodnoty predpätia rezovou metódou.
2.1 Betón
Po odskúšaní boli z jednej vzorky odvŕtané dva valce s priemerom 70 mm a výškou 140 mm. Bol použitý vrták s vonkajším priemerom 78 mm. Valce boli odobraté vo vodorovnom smere, keďže bolo potrebné sa vyhnúť predpínacím drôtom (Obr. 5). Z rovnakého dôvodu bol zvolený priemer odvŕtaných vzoriek. Stredná hodnota valcovej pevnosti betónu v tlaku fc,cyl bola určená na 63,3 MPa a stredná hodnota sečnicového modulu pružnosti Ec bola 37,4 GPa. Pri určovaní modulu pružnosti boli použité lepené odporové fóliové tenzometre HBM LY41-50/120 z feritickej ocele (teplotná odozva „1“: 10,8·10−6/K) s dĺžkou mriežky 50,0 mm a celkovou dĺžkou 63,6 mm.
2.2 Predpínacie drôty
Po aplikácii rezov boli, na jednom z predpätých betónových podvalov, odhalené horné predpínacie drôty. Následne boli odobrané dve vzorky na materiálové skúšky (Obr. 6). Skúškou bola medza pevnosti predpínacej výstuže (fpt) stanovená na strednú hodnotu 1736 MPa a medza klzu (fp,0,1) na strednú hodnotu 1547 MPa (Tab. 6.2). Vyhodnotenie bolo vykonané na zariadení Instron Universal Testing Machine s kapacitou do 200 kN v zmysle ISO 6892-1:2018. Test bol nastavený podľa parametrov odporúčaných v „metóde A“. Keďže priemer skúšaných predpínacích drôtov mal hodnotu 7 mm, plocha drôtu (Ap) bola 38,5 mm2.
2.3 Experimentálne meranie
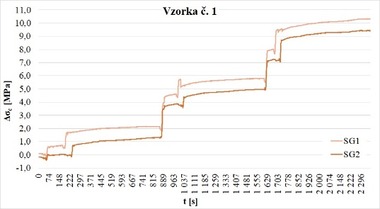
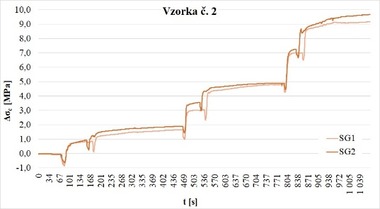
Na hornú hranu vzoriek predpätých betónových železničných podvalov boli v strednej časti aplikované celkovo tri rezy v osovej vzdialenosti 120 mm (Obr. 7). Podvaly boli počas experimentu v nezaťaženom stave (pôsobila iba vlastná tiaž podvalov a overované predpätie). Toto miesto aplikácie bolo zvolené z dôvodu jednoduchého prístupu a rovnej hrany podvalu v jeho strednej časti. Rezanie bolo vykonané postupne v troch samostatných krokoch s hĺbkami 10, 20 a nakoniec 30 mm (Obr. 8). Maximálna hĺbka rezov bola zvolená s ohľadom na polohu predpínacích drôtov, keďže cieľom bolo vyhnúť sa ich prerezaniu. Po každom kroku rezania (fáze) sa čakalo na stabilizáciu čítania zmeny pomerných pretvorení (normálových napätí), ktoré boli merané pomocou lepených odporových fóliových tenzometrov HBM LY41-50/120 z feritickej ocele (teplotná odozva „1“: 10,8×10−6/K) s dĺžkou mriežky 50,0 mm a celkovou dĺžkou 63,6 mm. Tenzometrické snímače boli umiestnené v polovici osovej vzdialenosti medzi rezmi. Na každej vzorke bola overená izolácia betónového bloku od vonkajšieho zaťaženia vždy na dvoch symetricky umiestnených tenzometroch z dôvodu kontroly správnosti merania a následného určenia reziduálnej predpínacej sily.
Vzorky boli pri experimente líniovo podopreté na valcových podperách vo vzdialenosti 100 mm od okrajov, čím sa vytvorila statická schéma jednoducho podopretého nosníka s rozpätím 2400 mm (Obr. 9). Toto podopretie bolo zvolené s ohľadom na následné vyhodnotenie nameraných výsledkov – jednoduché určenie príspevku vlastnej tiaže k hľadanému normálovému napätiu od predpätia. Mierne odskoky záznamov zmeny normálových napätí na tenzometrických snímačoch sú spôsobené tým, že jednotlivé rezy boli aplikované postupne.
Takto bol získaný v našom prípade súbor 6 meraní, ktorý sa ďalej štatisticky spracovával a vyhodnotil v kombinácii s teoreticky stanovenými, predpokladanými hodnotami na princípe podmienenej pravdepodobnosti a v Bayesovskom koncepte predstavuje tzv. doplnkovú hypotézu (likelihood). Príklad postupného vývoja zmeny pomerných pretvorení na hornej ploche betónu podvalu č. 1, v dvoch blokoch dokumentuje Obr. 10.
3. Aplikácia podmienenej pravdepodobnosti
Analytické alebo numerické výpočty predpokladanej úrovne predpätia v existujúcej konštrukcii sa považujú vo všeobecnosti za štandardný prístup, (Pcalc). Vstupné údaje aplikované do procesu učenia predpínacej sily sa získavajú ako výsledky diagnostiky a teda prirodzene majú silne stochastický charakter – apriórna hypotéza, resp. tzv. priórna pravdepodobnosť. Najmä pre materiálové parametre betónu, predpínacej výstuže a samozrejme značného vplyvu reologických procesov v podobe dotvarovania a zmrašťovania betónu, na predpínaciu silu v čase. Neistoty v získavaní dát (miesto merania, početnosť a pod.) je možné do veľkej miery eliminovať štatistickým spracovaním získaného súboru. Presnosť však závisí od rozsiahlosti súboru dát. Aby bolo možné relevantne spracovať výsledný náhodný jav (hypotéza), predstavujúci v našom prípade predpínaciu silu v čase, je potrebné zvyšné hodnoty dosimulovať, pričom je vhodné využitie niektorej zo simulačných techník, napr. metódu Monte Carlo (MC). Týmto spôsobom boli generované náhodné vektory všetkých vstupných premenných veličín (1000 hodnôt), ktoré definovali vstupné hypotézy pre podmienenú Bayesovskú pravdepodobnosť [6].
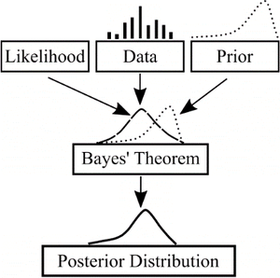
Bayesov princíp – zákon podmienenej pravdepodobnosti je vhodné využiť preto, lebo pri stanovení pravdepodobnosti neznámej veličiny vie komplementovať do systému dva alebo viacero závislých javov, resp. hypotéz [6]. Základný princíp je stručne opísaný na príklade dvoch javov (hypotéz) A a B. Podmienená pravdepodobnosť P(A|B) (nazývaná aj posteriórna pravdepodobnosť) javu A vzniká vtedy, ak jav B je pravdivý a nastal s nenulovou pravdepodobnosťou P(B). Graficky je možné proces stanovenia výsledného rozdelenia posteriórnej pravdepodobnosti spojitej náhodnej premennej (predpínacia sila Ppost) interpretovať nasledovne, (Obr. 11):
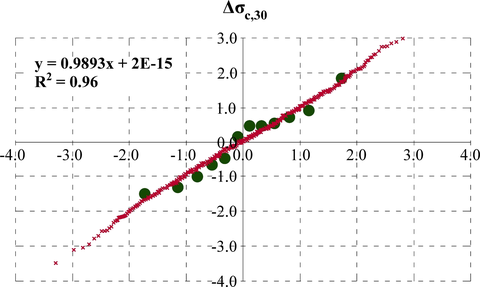
V prípade, že náhodné veličiny majú normálne rozdelenie, čo bolo v našom prípade verifikované testom spoľahlivosti Q-Q-plot pre doplnkovú hypotézy, Obr. 12.
Medzinárodná organizácia Joint Committee on Structural Safety (JCSS) v nosnom dokumente [6] odporúča využiť riešenie rovnice vyplývajúcej z princípu (2) v upravenom tvare a funkciu hustoty priórnej pravdepodobnosti vyjadriť v inžiniersky prijateľnej forme pomocou rozdelenia s μ a σ vo forme,
kde je
- k
- normalizačná konštanta,
- μ
- stredná hodnota,
- σ
- smerodajná odchýlka,
δ(n') = 0 pre n' = 0,
δ(n') = 1 pre n' > 0, - m'
- stredná hodnota súboru,
- s'
- štandardná odchýlka súboru,
- n
- veľkosť súboru,
- v' = (n − 1)
- počet stupňov voľnosti.
Toto rozdelenie pravdepodobnosti spojitej náhodnej veličiny je potom transformované podľa [5, 6] do posteriórnej pravdepodobnosti f''(μ, σ) za pomoci konjugácie doplnkovej hypotézy.
4. Vyhodnotenie Bayes konceptu
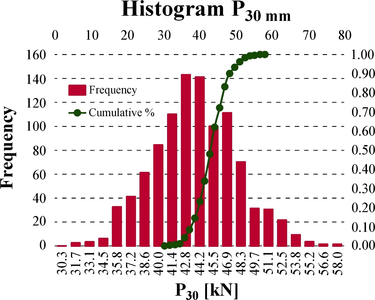
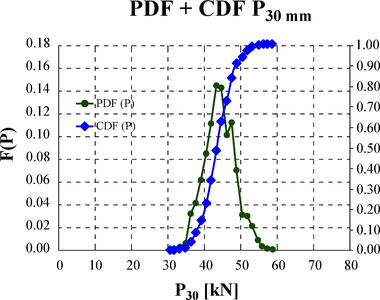
Vykonaná bola analýza na viacerých úrovniach rezov, avšak vzhľadom k rozsahu článku uvádzame len stanovenie rozdelenia náhodného vektora aktuálnej predpínacej sily, pre rezy s uvoľneným napätím na úrovni hĺbky 30 mm, Presidual = P30 = {P(30 mm)}. Tieto údaje sú ďalej na Obr. 13 dokumentované funkciami rozdelenia pravdepodobnosti vo forme PDF (distribučná funkcia hustoty pravdepodobnosti) a CDF (kumulatívna distribučná funkcia). V Tabuľke 1 sú prehľadne uvedené všetky hodnoty uvoľnených normálových napätí v jednotlivých rezoch.
| Vzorka | SG1 Δσc,i [MPa] | SG2 Δσc,i [MPa] | ||||
|---|---|---|---|---|---|---|
| Δσc,10 | Δσc,20 | Δσc,30 | Δσc,10 | Δσc,20 | Δσc,30 | |
| 1 | 2,14 | 5,78 | 10,32 | 1,31 | 4,92 | 9,44 |
| 2 | 1,56 | 4,80 | 9,16 | 1,90 | 4,89 | 9,68 |
| 3 | 1,48 | 4,11 | 8,02 | 1,49 | 4,24 | 8,16 |
| 4 | 1,37 | 4,72 | 9,38 | 1,50 | 4,74 | 9,28 |
| 5 | 1,31 | 4,39 | 8,37 | 1,22 | 4,45 | 9,55 |
| 6 | 1,42 | 4,74 | 8,73 | 1,21 | 4,26 | 8,60 |
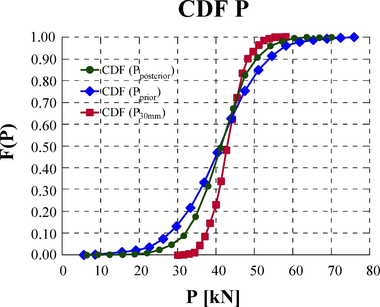
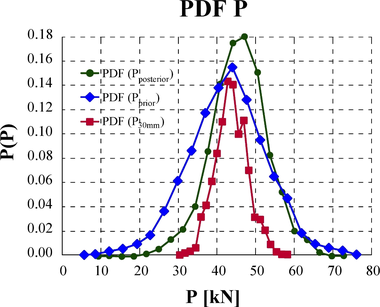
Prediktívny súbor údajov analyticky vypočítanej predpínacej sily {Pcalc} bol vyššie prezentovaný ako (priórna hypotéza) s funkciou rozdelenia náhodnej premennej f'(μ, σ) podľa rovnice (3). Náhodný vektor Presidual = {P(30 mm)} odvodený zo zmeny normálového napätia zodpovedajúci zvolenej hĺbke rezu bol aplikovaný v Bayesovskom modeli ako doplnková podmieňujúca hypotéza. Takáto funkcia založená na súbore nameraných údajov z rezovej metódy špecifikuje a aktualizuje výpočtovú predikciu. Výsledná distribučná funkcia predpínacej sily {Ppost = P}, je uvedená ako posteriórna pravdepodobnostná funkcia s rozdelením f''(μ, σ). Konjugáciu oboch funkcií je možné vykonať pomocou simulačných techník, napr. simulácie MC a výsledok možno graficky interpretovať vo funkciách rozdelenia pravdepodobnosti PDF a CDF – pre predpínaciu silu {Ppost}, Obr. 14.
5. Závery
Rozhodujúcim faktorom pri posudzovaní existujúcich predpätých betónových konštrukcií je stanovenie hodnoty predpínacej sily v danom čase. Objektívne určenie tejto hodnoty je vo všeobecnosti veľmi náročná úloha a vyžaduje si často len experimentálno-teoretický prístup. V prezentovanej štúdii boli zvolené ako testovacie telesá vopred predpäté železničné podvaly. Vzorky mali jasne definovanú hladinu predpätia s prakticky dokonalým technickým stavom, pričom boli testované rok po ich výrobe a boli uložené v stabilných podmienkach skladu. Úroveň predpínacej sily v čase bola stanovená štandardným výpočtom podľa Eurokódu 2 s uvážením príslušných strát predpätia a jej stredná hodnota bola, Pm,t = 40,96 kN. Simuláciou MC sa získal vektor náhodnej premennej s normálnou distribúciou, {Pcalc}. V tomto článku je uvedená doplnková hypotéza na základe experimentálnej rezovej metódy pre 30 mm hlboký rez, {P(30 mm)}. Následne Bayesovský koncept podmienenej pravdepodobnosti umožnil získať „najpravdepodobnejšiu“ hodnotu sledovanej náhodnej veličiny, {Ppost}. V našom prípade je stredná hodnota posteriórneho rozdelenia, Ppost = 41,34 kN. V tomto prípade obe funkcie vykazujú takmer zhodu. Avšak, ak by tvar, distribúcia a posun na osi X u prediktívnej funkcie a funkcie doplnkovej hypotézy boli vzdialené, funkcia rozdelenia posteriórnej pravdepodobnosti by bola významne rozdielna. Predpätie je kľúčovou informáciou pri určovaní únosnosti existujúcich predpätých betónových konštrukcií. Aplikácia Bayesovského modelu štatistického hodnotenia dokáže nepochybne veľmi objektivizovať tak silne stochastický jav, akým je stanovenie hodnoty aktuálnej úrovne predpätia v čase.
Poďakovanie
Tento príspevok vznikol za podpory Vedeckej grantovej agentúry MŠVVaŠ SR a SAV (VEGA) číslo 1/0306/21 a 1/0048/22 a Kultúrnej a edukačnej grantovej agentúry MŠVVaŠ SR (KEGA) číslo 020ŽU-4/2021.
Literatúra
- Moravčík, M. – Bujňáková, P. – Bahleda, F.: Failure and damage of a first-generation precast prestressed bridge in Slovakia. Structural Concrete 2020, 21, 2353–2362, https://doi.org/10.1002/suco.201900526.
- Bagge, N. – Nilimaa, J. – Elfgren, L.: In-situ Methods to Determine Residual Prestress Forces in Concrete Bridges. Engineering Structures, 2017.
- Kraľovanec, J.: Možnosti analýzy predpätia existujúcich betónových konštrukcií, Dizertačná práca, Žilinská univerzita v Žiline, 2022, Žilina.
- Kraľovanec, J. – Moravčík, M. – Koteš, P. – Matejov, A.: Parametric Study of Saw-Cut Method. XXX Russian-Polish-Slovak Seminar Theoretical Foundation of Civil Engineering (RSP 2021). In Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2021; Volume 189, 10-19. https://doi.org/10.1007/978-3-030-86001-1_2.
- Botte, W. – Vereecken, E. – Taerwe, L. – Caspeele, R.: Assessment of posttensioned concrete beams from the 1940s: Large-scale load testing, numerical analysis and Bayesian assessment of prestressing losses. Structural Concrete 2021, 22(5)
- JCSS: Probabilistic Model Code, Online: https://www.jcss-lc.org/jcss-probabilistic-model-code/, 2001.


![Obr. 3a – Parametre skúšaných predpätých podvalov typu B70 W-49 G, rozmery v [mm]](/docu/clanky/0252/025211o6.png)
![Obr. 3b – Parametre skúšaných predpätých podvalov typu B70 W-49 G, rozmery v [mm]](/docu/clanky/0252/025211o8.png)




![Obr. 7 – Schéma rezov (SC) a tenzometrov (SG), rozmery v [mm]](/docu/clanky/0252/025211o22.png)