Výpočet seizmicky zatížených zárubních a opěrných zdí
Eurokód 1998-5: Navrhování konstrukcí odolných proti zemětřesení popisuje výpočet pomocí metody Mononobe-Okabe. Tento zjedndušený kvazi-statický postup je částečně velmi konzervativní. Článek popisuje limity této metody a porovnává metodu Mononobe-Okabe s přístupem americké NHCRP 661 a s metodou Chen a Liu.
1. Úvod
Teorie Coulomba a Rankina vytvořily základ pro dnes běžně používané teorie výpočtu zemního tlaku. V průběhu 20. století bylo zjištěno, že zemní tlaky při seizmickém působení mohou být výrazně vyšší než v případě čistě statických zatěžovacích stavů. Okabe (1924) a Mononobe & Matsuo (1929) představili první metodou, která dokázala vypočítat celkový zemní tlak od statického a seizmického zatížení. Tato metoda se stala známou jako metoda Mononobe–Okabe (dále M-O) a doporučuje se v mnoha geotechnických normách. Také Eurokód 1998-5 pro návrh opěrných a zárubních zdí v seizmických podmínkách uvádí výpočet s použitím této metody. Metoda M-O jakožto zjednodušený kvazistatický postup je částečně velmi konzervativní. V článku jsou popsány limity této metody, porovnání s ostatními přístupy pro výpočet seizmicky zatížených zárubních zdí v americké NHCRP 661 a metodě Chen a Liu (1990).
2. Seizmické zatížení
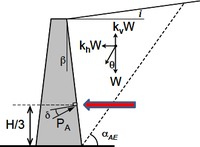
Pro kvazistatické výpočty zárubních a opěrných zdí je seizmické zatížení zeminou dáno vodorovnými a svislými silami, které jsou rovny tíze aktivního klínu W a příslušného seizmického součinitele kh, kv (viz Obr. 1). Svislé zatížení musí být uvažováno tak, aby působilo nejnepříznivější účinek. Velikost seizmického součinitele je obecně určitá hodnota poměru posuzovaného zrychlení a gravitačního zrychlení a je možné ji určit vztahy podle různých autorů:
Podle Terzaghiho (1950)
kde je
- ah
- návrhové zrychlení ve vodorovném směru,
- av
- návrhové zrychlení ve svislém směru,
- g
- gravitační zrychlení.
Podle Gutenberga a Richtera (1956)
kde je
- a0
- zrychlení zemětřesení o magnitudu Ms.
Podle Eurokódu 1998-5
kde je
- r
- součinitel dle Tab. 1.
Pro stěny nižší 10 m musí být seizmický součinitel po výšce konstantní. Pro určení vlivu vyšších stěn na hodnotu seizmického zatížení Eurokód 1998-5 neudává postup.
| Typy opěrné nebo zárubní konstrukce | r |
|---|---|
| Volné gravitační zdi, které se mohou vychýlit až do dr = 300 α ∙ S [mm] | 2 |
| Volné gravitační zdi, které se mohou vychýlit až do dr = 200 α ∙ S [mm] | 1,5 |
| Pružné betonové stěny, kotvené nebo rozepřené stěny, železobetonové stěny založené na svislých pilotách, vetknuté základové stěny a mostní opěry | 1 |
| Pozn. α je poměr návrhového zrychlení ag pro základovou půdu typu A ke gravitačnímu zrychlení g, S je součinitel podloží definovaný v Eurokódu 1998-1 | |
Podle NCHRP 611 a AASHTO
National Cooperative Highway Research Program (NCHRP) je výzkumný program Spojených států amerických. Výzkum v oblasti silniční infrastruktury je financován z American Association of State Highway and Transportation Officials (AASHTO – asociace amerických silnic a dopravců). Zpráva 611 uvádí současné výsledky z výzkumu seizmického návrhu silniční infrastruktury včetně svahů a nosných konstrukcí. Základy seizmického zrychlení se nenacházejí v samotné zprávě NCHRP 611, ale v nadřazeném dokumentu: Specifikace návrhu mostu LRFG (AASHTO, 2007 a 2012). Zpráva 611 NCHRP se týká této zprávy v kapitolách 5 a 7, a to především součinitele α, který zohledňuje výšku zásypu:
kde je
- kh,NCRHP
- vodorovný seizmický součinitel khd podle definice v AASHTO (2007/2012) [–],
- Fpga
- faktor lokality pro nulovou periodu v spektru pružné odezvy – hodnoty v tabulce 3.10.3.2-1 AASHTO (2012) [–],
- PGA
- špičkové zrychlení v úrovni terénu pro skalní podloží (třída B) [m/s2],
- α
- součinitel výšky zásypu [–],
- g
- gravitační zrychlení (9,81 ms−2).
Součinitel výšky násypu α popsaný ve zprávě 611 NCHRP je výsledkem jednorozměrné analýzy šíření vln ve volném poli. Při analýze byla vzata v úvahu skutečnost, že zrychlení zásypu opěrné konstrukce není na žádném místě stejné v jakémkoli okamžiku. Tento součinitel lze vypočítat pro zeminy třídy C, D a E (ekvivalentní všem zeminám kromě skály a velmi měkké hlíny) podle AASHTO takto:
kde je
- H
- výška nosné konstrukce nebo zásypu [m],
- Fv
- faktor lokality pro dlouhodobý rozsah v spektru pružné odezvy podle tabulky 3.10.3.2-3 AASHTO (2012) [–],
- S1
- Součinitel vodorovného spektrálního zrychlení pro periodu 1 s v hornině (třída B) [m/s2].
Vzorec (9) lze však použít pouze tehdy, je-li výška nosné konstrukce H > 6 m. Pro stavbu výšky H ≥ 30 m musí být výška v rovnici (9) nastavena na hodnotu H = 30 m. Součinitel výšky zásypu koresponduje s funkcí korekčního faktoru qh podle švýcarské SIA 267.
3. Metoda Mnonobe–Okabe
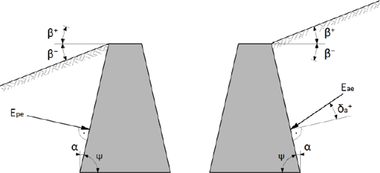
Na základě zemětřesení v japonském Kanto roku 1923 provedli Okabe (1924) a Mononobe & Matsuo (1929) řadu pokusů na vibračním stole. Na základě získaných experimentálních výsledků byla odvozena pseudostatická metoda (zavádějící princip ekvivalentních zrychlení) pro výpočet celkového zemního tlaku od statického a seizmického zatížení. Tato metoda (známá jako metoda Mononobe–Okabe) na základě Coulombova limitního přístupu a předpokladu, že zemní tlak vyvodí tuhé těleso, které se posouvá po šikmé ploše, udává vztahy pro aktivní nebo pasivní zemní tlak při seizmickém zatížení (znaménková konvence je na Obr. 2):
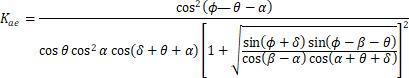 (12)
(12)
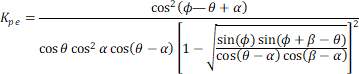 (13)
(13)
kde je
- γ
- objemová tíha zeminy [kN/m3],
- H
- výška nosné konstrukce [m],
- Kae
- součinitel aktivního zemního tlaku (statický + dynamický),
- Kpe
- součinitel pasivního zemního tlaku (statický + dynamický),
- β
- sklon svahu za opěrnou zdí [°]
- α
- sklon rubu zdi [°]
- ϕ
- úhel vnitřního tření materiálu zásypu [°]
- δ
- úhel tření mezi zeminou a konstrukcí zdi [°]
- kh
- seizmický koeficient vodorovného zrychlení [–]
- kv
- seizmický koeficient svislého zrychlení [–]
V mnoha případech se seizmický koeficient svislého zrychlení kv v těchto vzorcích zanedbává, protože vliv svislého zrychlení je poměrně malý.
3.1 Limity metody Mnonobe–Okabe
Vztahy metody M-O jsou založeny na následujících předpokladech Mohr-Coulombovy teorie porušení zeminy s kritériem podle teorie Coulomba:
- suchý, homogenní, izotropní zásypový materiál,
- zemina nad smykovou plochou je pevná – vytvoří klín,
- zemina pod opěrnou konstrukcí je únosná,
- seizmické zatížení je modelováno jako statická síla (násobek kh,d),
- stěna musí být schopna posunu či otočení tak, aby mohla v zemině vzniknout smyková plocha,
- vzniklá smyková plocha je rovinná,
- terén nad zdí je modelován jako nekonečně dlouhý svah.
Poslední dva body v tomto výčtu jsou zodpovědné za problémy s použitím metody M-O.
Pokud sklon svahu (zásypu) za zdí β dosáhne nebo překročí sklon smykové plochy, výsledkem je nekonečně velký „klín“ zeminy. To má za následek, že spočtený aktivní zemní tlak je nekonečně velký a vztahy metody M-O již pro tyto sklony neposkytují řešení. Důkaz omezené platnosti vztahu (12) lze jednoduše ukázat na příkladu určení stability nekonečně dlouhého svahu s rovinnou smykovou plochou, kdy je svah tvořen nesoudržnou zeminou a není v něm voda. Seizmické zatížení je dáno horizontálním zrychlením kh,d = ah,d / g a vertikální zrychlení kv,d je zanedbáno. Je známo, že takovýto svah je stabilní, pokud je sklon β menší než úhel (φ − θ) popř. v extrémním případě β = φ − θ, kdy smyková plocha je přesně rovnoběžná se sklonem povrchu. Při použití vztahu (3) pro součinitel aktivního zemního tlaku pro kh,d = 0,1; β = 30°, ϕ = 35°, se výraz sin (φ − β − θ) pod odmocninou stane záporným a nelze nalézt žádné přirozené řešení.
Metoda M-O má pouze omezenou vhodnost pro výpočet pasivního zemního tlaku od seizmického zatížení. Smyková plocha u pasivního zemního tlaku nemusí být uvažována jako vodorovná, ale logaritmická. Pokud porovnáme hodnoty pasivního zemního tlaku pro logaritmický tvar smykové plochy a pro vodorovný (ten uvažuje metoda M-O), vidíme, že pro rovinnou plochu může dojít k značnému nadhodnocení odolnosti vůči pasivnímu zemnímu tlaku zvláště při uvažování úhlu tření mezi zeminou a konstrukcí zdi δ = −2/3 φ. Poslední nevýhodou metody M-O je předpoklad konstantního seizmického zatížení po celé výšce konstrukce (tj. i zemního klínu).
4. Eurokód 1998-5
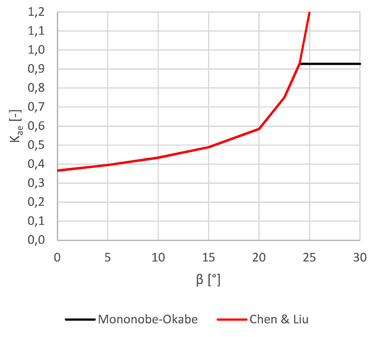
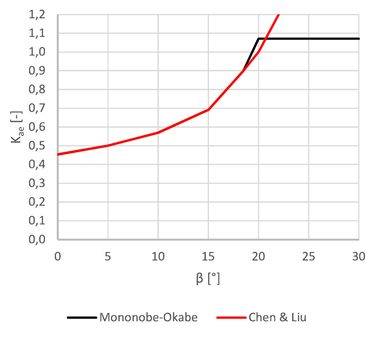
Příloha E Eurokódu 1998-5 udává dva vzorce pro výpočet součinitele aktivního zemního tlaku Kae. Pro sklon povrchu terénu za zdí β ≤ φ − θ používá rovnici podle M-O (12). V případě, že sklon svahu za zdí splňuje podmínku β > φ − θ, je původní vztah upraven úplným vyloučením vlivu sklonu povrchu terénu za zdí β:
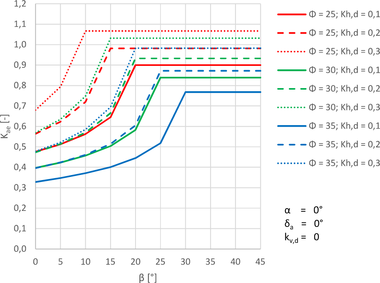
Pro sklony terénu za zdí o hodnotách úhlu β > φ − θ tedy vzniká mez, kde původní vztah (12) vypočítá nekonečný součinitel zemního tlaku Kae, ale vztah (14) dává konstantní hodnotu součinitele Kae. Sklon terénu za opěrnou zdí může být tedy podle vtahu (14) libovolně zvětšen nad hodnotu φ − θ, aniž naroste zemní tlak (viz Obr. 3). Takto při nepozornosti může uniknout skutečnost, že je svah nad stěnou již nestabilní a teoreticky celá oblast (!) musí být podepřena nosnou konstrukcí tak, aby nenastal její posun. Proto je použití vzorce (14) nevhodné v případě velmi strmých sklonů terénu nad zdí. Výpočty pro tento článek byly provedeny v programu GEO5, který má mimo jiné postup podle Eurokódu 1998-5 zabudovaný. Výhodou tohoto programu je, že při hodnotách sklonu β > φ − θ upozorňuje uživatele na tuto skutečnost a možné problémy.
Pro výpočet součinitele pasivního zemního tlaku Kpe používá Eurokód 1998-5 vztah (13), který však doporučuje používat především pro svislý líc stěny. Navíc požaduje uvažovat tření mezi stěnou a zeminou δp = 0° (článek 7.3.2.3 (6)), což vede k velmi konzervativním výsledkům.
5. Chen a Liu
Metoda Chen a Liu vychází z doktorské práce Changa (1981). Stejně jako metoda M-O je založena na kinematickém přístupu. Nicméně místo vodorovné smykové plochy uvažuje logaritmickou smykovou plochu. Chen a Liu (1990) uvádí pro nejběžnější případy i tabulkové hodnoty. Tato metoda poskytuje nižší pasivní zemní tlaky než metoda M-O (pro stejnou hodnotou tření mezi stěnou a zeminou).
6. NCHRP 611
Metoda Shamsabadi (2007), doporučená normou NCHRP 611, je kinematická metoda, která uvažuje logaritmickou smykovou plochu a hyperbolický vztah mezi napětím a deformací. Tím se tato metoda liší od běžných kinematických metod, jako je např. Chen a Liu (1990). Norma NCHRP 611 (2008) v dodatku 5 uvádí grafy pro součinitel pasivního zemního tlaku Kpe jako funkce proměnných: soudržnosti zeminy c, výšky stěny H, objemové tíhy zeminy γ seizmického součinitele kh a úhlu vnitřního tření zeminy φ.
7. Porovnání metod s aktivním seizmickým zemním součinitelem
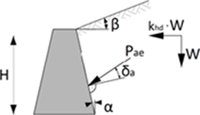
Pro srovnání metod Chen a Liu a M-O byl záměrně zvolen jednoduchý případ: tížná zeď se svislou rubovou stěnou (α = 0°) o výšce H = 3 m a s úhlem tření stěny δ = 2/3 φ, sklon povrchu terénu β = 0° až 30°, úhel tření zeminy φ = 30°, soudržnost c = 0 kPa. Vertikální zrychlení zemětřesení bylo zanedbáno, horizontální zrychlení kh,d je 0,1, respektive 0,2 (viz Obr. 4).
Rozdíly mezi metodami jsou velmi malé do kritického sklonu povrchu terénu β (viz Obr. 5 vlevo). Důvodem je to, že pro zde provedené výpočty součinitele aktivního zemního tlaku se smyková logaritmická smyková plocha stává prakticky rovnou. Zvláštnost metody Chen a Liu (1990) je zřejmá z diagramu na Obr. 5 vpravo, kde je vidět, že metoda dává výsledky i pro svahy zásypu nad kritický sklon β, ačkoli pro velmi strmé svahy jsou to hodnoty již nad fyzicky přípustnou mez (a svah by byl nestabilní).
Obr. 5: Srovnávací výpočty vlivu soudržnosti na aktivní seizmický zemní tlak (pro kh = 0,1 – vlevo, pro kh = 0,2 – vpravo)
8. Porovnání metod s pasivním seizmickým zemním součinitelem
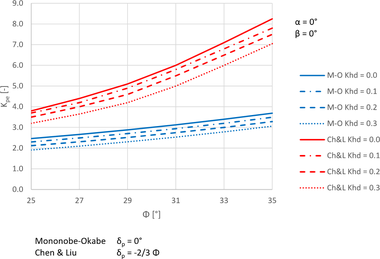
Pro srovnání hodnot součinitele pasivního zemního tlaku Kpe podle Chen a Liu (1990) a Eurokódu 1998-5 (viz Obr. 6) byla zvolena tížná zeď se svislou rubovou stěnou (α = 0°) o výšce H = 3 m s vodorovným povrchem za zdí β = 0°. Pro metodu Chen a Liu (1990) byl úhel tření stěny δ = −2/3 φ a pro Eurokód 1998-5 δ = 0° (předepsáno normou), úhel vnitřního tření φ byl uvažován od 25° do 35°. Vertikální zrychlení zemětřesení bylo zanedbáno, horizontální zrychlení kh nabývalo hodnot 0; 0,1; 0,2 a 0,3.
Podle literatury dává postup podle Eurokódu 1998-5 pro δ = 0° (což odpovídá jeho požadavkům) nejkonzervativnější hodnoty ze všech metod. Pokud by se pro tření mezi stěnou a zeminou použila hodnota δ = −2/3 φ, získaly by se vyšší koeficienty pasivního zemního tlaku než u metody podle Chen a Liu (1990). Jelikož je však mnohé odvození koeficientu pasivního seizmického tlaku Kpe uváděné v odborné literatuře kontroverzní, je doporučeno používat výpočet pomocí metody M-O podle EC 8 (δp = 0°).
9. Závěr
Je třeba poznamenat, že metoda M-O představuje velmi velké zjednodušení reality. Vedle omezení, která mají všechny pseudostatické metody, je nutné zejména uvést, že se při seizmickém zatížení nezohledňuje kmitočtový rozsah buzení ani tuhost zeminy. Přes veškerá omezení a možné nedostatky se metoda M-O stále používá jako snadno srozumitelná a smysluplná metoda pro výpočet seizmických zatížených opěrných konstrukcí. Eurokód 1998: Navrhování konstrukcí odolných proti zemětřesení – Část 5: Základy, opěrné a zárubní zdi a geotechnická hlediska se v příloze E výslovně odkazuje na tuto metodu. V případě řešení problému s hodnotou sklonu terénu β dostáváme však u Eurokódu 1998-5 od kritického sklonu již konstantní hodnoty součinitele aktivního zemního tlaku Kae. V případě výpočtu pasivního zemního tlaku dává postup podle Eurokódu 1998-5 při požadavku tření mezi stěnou a zeminou δp = 0° (v 7.3.2.3) velmi konzervativní výsledky. V obou výše uvedených případech se jeví výhodnější použití metody Chen a Liu. Při výpočtu stěn vyšší než 10 m neudává Eurokód 1998-5 postup určení seizmického zatížení (na rozdíl od americké NCHRP 611).
10. Literatura
- AASHTO. LRFD Bridge Design Specifications. 4th Edition, American Association of State Highway and Transporta-tion Officials, Washington DC, 2007
- ČSN EN 1998-5 Navrhování konstrukcí odolných proti zemětřesení – Část 5: Základy, opěrné a zárubní zdi a geotechnická hlediska, 2006
- FHWA (Federal Highway Administration). Seismic Retrofitting Manual for Highway Structures: Part 1 – Bridges, 2006
- GEO5. Uživtelský manuál, https://www.fine.cz/
- GUTENBERG, B., RICHTER, C. F. Magnitude and Energy of Earthquakes, Annali di Geofisica, 9: 1–15, 1956
- CHEN, Wai-Fah; LIU, X. L. Limit analysis in soil mechanics, Elsevier, 1990
- MONONOBE, N., MATSUO, H. On the Determination of Earth Pressure during Earthquake, paper no. 388, Proceedings of World Engineering Congress. Marunouchi, Tokyo (Vol. 9), S. 177–185, 1929
- NCHRP 611 Seismic Analysis and Design of Retaining Walls, Buried Structures, Slopes and Embankments, 2008
- OKABE, S. General Theory of Earth Pressures, Japan Society of Civil Engineering (Vol. 12), 1926
- PRUŠKA, J. Dynamika geotechnických konstrukcí, ČVUT FSv, 2017
- SHAMSABADI, A. Three-Dimensional Nonlinear Seismic Soilabut-ment-Foundation-Structure Interaction Analysis of Skewed Bridges, University of Southern California, 2007
- TERZAGHI K. Mechanisms of Landslides, Application of geology to engineering practice, Geological Society of America, Berkeley,1950
Poděkování
Příspěvek byl uveřejněn za souhlasu ČGtS ČSSI, která vlastní autorská práva na originální verzi článku publikovanému ve sborníku příspěvků z konference Zakládání staveb Brno 2020.
Metoda Manonobe-Okabe je jedním z přístupů, jak stanovit zatížení od seismicity, přírodního, nebo technického původu, které bude působit na geotechnické konstrukce, například opěrné zdi. Informace o možnostech této metody se v českých odborných zdrojích zatím neobjevily. Tento článek zprostředkovává českým čtenářům bližší poznatky o této metodě a rovněž ukazuje oblasti jejího potenciálního využití v geotechnice.
Souhlasím s publikováním článku v odborném periodiku TZB.
Eurocode 1998-5 for the design of earth retaining structures in seismic conditions describes calculation using the Mononobe-Okabe method. This simplified quasi-static procedure is partly very conservative. The article describes the limits of this method, comparison with other approaches in American NHCRP 661 and Chen and Liu method.