Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Problematika výberu vstupných údajov do počítačového modelovania popisujúceho prenos tepla v drevenom nosníku zaťaženém požiarom

17.2.2025

Ing. Dominik Špilák, PhD., Technická univerzita vo Zvolene, Slovensko

Recenzovaný

Cieľom príspevku je poukázať, aký vplyv na výsledky počítačového modelovania prenosu tepla v drevenom nosníku zaťaženéhom požiarom majú vstupné údaje o materiálových vlastnostiach a ako je možné zvýšiť presnosť výsledkov počítačového modelovania. Metodika práce pozostávala z vykonania požiarnych skúšok ako základu pre model konečných prvkov s implementáciou 6 rôznych nastavení materiálových vlastností na základe výstupov zo strednodobých skúšok. Výsledky modelovania boli navzájom porovnané so skutočnými požiarnymi skúškami pomocou koeficientu spoľahlivosti. Výsledky simulácií ukázali dôležitosť úpravy vstupných údajov.

Pri nastavení založenom na Eurokóde 5 výsledky modelovania neodrážajú fázovú zmenu vody začínajúcu pri 100 °C. V prípade nastavenia založeného na entalpii sa ukázalo, že len s pomocou entalpie výsledky modelovania nevykazovali dobrý priebeh teploty v oblasti, kedy dochádza k odparovaniu vody z dreva. Výrazný posun v presnosti výsledkov nastal po úpravách tepelnej vodivosti s pomocou T-history metódy, kedy sa presnosť zvýšila na 98,691 % s takmer dokonalým napodobnením teplotného priebehu počas fázovej premeny vody.

Úvod

Počítačové modelovanie založené na analýze konečných prvkov (FEA) je v súčasnej dobe takmer neodmysliteľnou súčasťou procesu návrhu stavieb a konštrukcií. Poskytuje množstvo neoceniteľných výhod, pričom výsledky modelovania dokážu užívateľom poskytnúť predstavu, ako sa pravdepodobne bude materiál alebo konštrukcia správať pri určitom zaťažení. Jednou z najťažších úloh pri vytváraní počítačového modelu je správne zadanie vstupných údajov, a to predovšetkým materiálových charakteristík. Pokiaľ sa hneď na začiatku zadajú nesprávne vstupné údaje, výsledky modelovania budú od počiatku zaťažené výraznou chybou [1].

Náročnosť zadávania správnych vstupný údajov sa zvyšuje, pokiaľ je potrebné modelovať správanie sa materiálov, ktoré majú v rôznych smeroch rôzne vlastnosti, akými sú napríklad drevo alebo materiály na báze dreva. Náročnosť ďalej zvyšuje aj fakt, že obsah vlhkosti výrazne mení materiálové vlastnosti dreva [2, 3]. Výsledky modelovania drevených konštrukcií sa preto len veľmi ťažko porovnávajú s výsledkami z reálnych testov a dosahuje sa tak relatívne nízka presnosť výsledkov. Kľúčom k správnemu návrhu počítačového modelu a jeho validáciu je zber informácií z reálnych testov väčšieho množstva vzoriek. Pripravený model sa následne validuje na priemerné hodnoty získané z reálnych testov. Týmto spôsobom je možné dosiahnuť najpresnejších výsledkov pri simuláciách správania sa nehomogénnych materiálov vystavených tepelnému namáhaniu.

Cieľom príspevku je poukázať, aký vplyv na výsledky počítačového modelovania prenosu tepla v drevenom nosníku zaťaženém požiarom majú vstupné údaje o materiálových vlastnostiach a ako je možné zvýšiť presnosť výsledkov počítačového modelovania.

Základom pre dosiahnutie správnych výsledkov z počítačového modelovania prenosu tepla v dreve je správne zadanie vstupných údajov o materiálových vlastnostiach dreva. Kľúčové premenné sú tepelná vodivosť, hmotnostná tepelná kapacita, hustota dreva a entalpia [4], pričom všetky tieto vlastnosti sú závislé na teplote. Tepelná vodivosť dreva bola skúmaná viacerými autormi. Naser [5] a Maraveas [6] vykonali vo svojej štúdii komplexné porovnanie nameraných hodnôt tepelnej vodivosti rôznych druhov dreva zaťažených požiarom od rôznych autorov [1–5, 7–12]. Poukázali na vysoký rozptyl nameraných hodnôt tepelnej vodivosti dreva v dôsledku diverzity testovaných drevených vzoriek. Tepelná vodivosť dreva je závislá na jeho hustote, obsahu vlhkosti a smere vlákien. Podľa Friquina [13] a Penga [14] tepelná vodivosť dreva je vyššia v smere pozdĺž vlákien ako kolmo na vlákna. Çavuş a kol. [15] skúmali tepelnú vodivosť 31 rozličných druhov dreva, pričom poukázali na lineárnu závislosť medzi hustotou dreva a jeho tepelnou vodivosťou vyjadrenú nasledovným vzťahom:

(1)

kde je

y: hustota dreva,
x: tepelná vodivosť dreva.

Jang a Kang [16] skúmali vplyv hustoty na tepelnú vodivosť 15 vzoriek dreva a tiež poukázali na to, že tepelná vodivosť dreva rastie s jeho hustotou. Na základe výskumov drevo s nízkou hustotou má bežne nižšiu tepelnú vodivosť. Čo následne vedie k rýchlejšiemu nárastu teploty povrchu, pyrolýze a skoršiemu začiatku uhoľnatenia. Naproti tomu, drevo s vyššou hustotou má vyššiu tepelnú vodivosť, vyššiu teplotu v reze, nižší teplotný gradient, nižšiu teplotu ohrievaného povrchu, avšak pyrolýza prebieha naprieč drevom rýchlejšie [4].

Obsah vlhkosti vplýva na proces transportu tepla v dreve niekoľkými spôsobmi. Limam a kol. [17], Krišťák a kol. [18] a Alegri a kol. [19] ukázali, že zvýšenie vlhkosti vzoriek vedie k zvýšeniu hodnoty tepelnej vodivosti dreva. Vololonirina a kol. [20] ukázali, že zmeny tepelnej vodivosti v závislosti na vlhkosti mali viditeľný lineárny trend, Mvondo a kol. [21] našli relatívne lineárny trend, podľa Zviceviciusa a kol. [22] stúpala tepelná vodivosť s obsahom vlhkosti s viac alebo menej výrazným zakrivením v závislosti od povahy materiálu. Aj napriek značnému rozptylu tepelnej vodivosti rozličných drevín a drevených materiálov v závislosti od vlhkosti je evidentné, že tepelná vodivosť s nárastom vlhkosti dreva rastie [23] (rov. 2).

(2)

kde je

λ_ω: tepelná vodivosť dreva pri vlhkosti ω [W·m⁻¹·K⁻¹],
ω: výsledná vlhkosť dreva [%],
ω₀: počiatočná vlhkosť dreva [%],
λ_ω₀: počiatočná tepelná vodivosť dreva pri vlhkosti ω₀ [W·m⁻¹·K⁻¹].

Predchádzajúci vzťah (2) má teplotné obmedzenie 100 °C, kedy dochádza k fázovej zmene obsiahnutej vody v dreve, po prekročení tejto teploty už nemá vlhkosť dreva zásadný vplyv na jeho tepelnú vodivosť.

Počas procesu ohrevu dreva pri požiari dochádza k fázovej zmene vody obsiahnutej v dreve. Nastáva tak stav, kedy sa prijatá energia nespotrebováva na ohrev dreva, ale hlavne na zmenu skupenského stavu vody [2, 6, 13, 24–31]. Tento efekt je viditeľný na teplotných krivkách získaných počas požiarnych testov dreva vyrovnaním teploty v oblasti okolo 100 °C po určitý čas, až kým sa neodparí všetka voda z dreva [7]. Voda obsiahnutá v dreve sa správa ako retardér pyrolýzy, pretože vstrebáva prijatú energiu a ochladzuje drevo. Čím je vyššia vlhkosť dreva, tak pri rovnakej dodanej energii je dosiahnutá teplota v dreve nižšia [2, 6, 13, 24–26, 28–32].

Hmotnostná tepelná kapacita, označovaná niekedy aj ako špecifické teplo, je definovaná ako množstvo tepelnej energie, ktorú musíme materiálu o jednotkovej hmotnosti dodať, aby jeho teplota narástla o jednu jednotku. Rovnako ako pri tepelnej vodivosti dreva, Naser [5] urobil porovnanie nameraných hodnôt od rôznych autorov [7, 9, 33–36] a poukázal na značný rozptyl hodnôt. Takmer všetci autori namerali zvýšené hodnoty tepelnej kapacity v rozmedzí od 100 do 120 °C, ktoré korešpondovali s odporúčanými hodnotami z Eurokódu 5 [9]. Vzniknutý skok je zapríčinený opäť zmenou skupenstva vody. Za povšimnutie stojí presne definovaný interval od 100 do 120 °C, ktorý je uvádzaný aj v Eurokóde 5 [9] a je zovšeobecnením pre všetky dreviny. Takto presne definovaný interval neodráža skutočnosť a rozdielnosť drevín, ich priepustnosť, pevnosť vlákien, vlhkosť a hustotu.

V materiáloch, v ktorých dochádza k akejkoľvek fázovej premene, je dôležité poznať teplotu, pri ktorej začína a končí fázová premena. Zhang a kol. ukázali [37], že teploty je možné určiť pomocou T-history metódy. Výpočet bol založený na základe zistenia minima druhej derivácie, inflexného bodu a maxima prvej derivácie teplotných kriviek zistených z reálnych požiarnych skúšok. Následne sa zistia priesečníky dotyčníc z týchto bodov, výsledné dva body predstavujú hranice fázovej premeny.

Drevo je možné chápať ako organický kompozitný materiál (drevo-voda) v dôsledku prítomnosti či už voľnej alebo viazanej vody. Pri dosiahnutí teploty vyparovania vody dochádza v sústave k fázovej zmene, ktorá sa prejavuje zmenou materiálových vlastností. Vplyv vyparovania vody na tepelnú vodivosť zatiaľ nebol bližšie preskúmaný [38]. Autori skúmajúci hodnoty tepelnej vodivosti dreva pri zvýšených teplotách robili merania mimo oblasť teplôt, kde dochádza k fázovej premene vody [1–5, 7–12].

Meranie tepelnej vodivosti materiálov počas fázovej premeny je možné vykonať dvomi postupmi, a to za stacionárnych podmienok alebo nestacionárnych, ako napríklad pomocou metódy LFA (laser flash method). LFA je bežne používaná na meranie tepelnej difuzivity α a tepelnej vodivosti κ podľa nasledovnej rovnice:

(3)

kde je

ρ: hustota,
C: tepelná kapacita.

Podľa Chena a kol. [39] v materiáloch, v ktorých dochádza k fázovej premene, dochádza k extra výmene energie potrebnej pre zmenu vnútornej energie materiálu. Za týmto účelom upravili rovnicu transportu tepla vložením vzťahu pre fázovú premenu, čím ukázali, ako fázová premena ovplyvňuje merania tepelnej vodivosti materiálov (rov. 4).

(4)

kde je

ΔS: plocha,
κ: tepelná vodivosť,
∆H: zmena entalpie,
C: tepelná kapacita,
ρ: hustota.

Chen a kol. [39] a Mathur a kol. [40] taktiež ukázali, že v odlišných materiáloch v dôsledku nárastu teploty dochádza počas fázovej zmeny k prudkej zmene tepelnej vodivosti, pričom maximá boli zaznamenané približne uprostred teplotného intervalu ohraničujúceho fázovú premenu.

Materiál a metodika

Metodika práce bola rozdelená na dve hlavné časti. Prvou časťou bolo vykonanie strednorozmerového testu dreveného nosníka zo smrekového dreva zaťaženého sálavým zdrojom tepla. Cieľom testu bolo získanie informácií o teplotných priebehoch vo vnútri nosníka počas požiarnej skúšky a získanie informácií o počiatočnej hustote a vlhkosti dreveného nosníka. Druhou časťou bolo vytvorenie modelu konečných prvkov a vykonanie FEA dreveného nosníka zaťaženého požiarom pri použití rôznych nastavení materiálových vlastností.

Strednorozmerové požiarne testy

Obr. 1 Strednorozmerová skúška

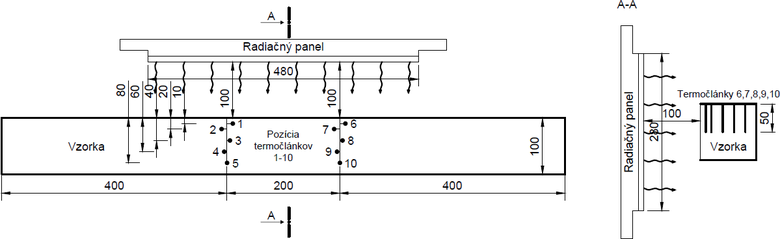
Teplotné priebehy v čase boli vyhodnotené na základe strednorozmerovej požiarnej skúšky (obr. 1). Na strednorozmerové skúšky boli použité drevené nosníky zo smreka obyčajného (Picea abies). Jednalo sa o hranoly s rozmerom strany 100 mm a dĺžkou 1000 mm. Testované vzorky neboli vysušené. Priemerná hustota a vlhkosť bola stanovená gravimetrickou metódou zo 6 vzoriek s rozmerom hrany 100 mm z toho istého kmeňa stromu zo strednorozmerových požiarnych skúšok. Skúškam boli podrobené štyri testované vzorky vyrobené z kmeňa jedného stromu.

Strednorozmerové skúšky trvali 30 minút, počas ktorých sa zaznamenávali teplotné priebehy na vopred určených miestach testovanej vzorky. Priebehy teplôt boli snímané pomocou termočlánkov NiCr-Ni (Omega Engineering Inc., Norwalk, CT, USA) s rozsahom merania −40 °C až +1200 °C. Umiestnenie termočlánkov v testovanej vzorke je uvedené na obrázku 2.

Obr. 2 Pozícia termočlánkov vo vzorke

Celkom 10 termočlánkov v 2 skupinách bolo umiestnených na vopred definovaných miestach v strede vzorky v hĺbke 50 mm. Termočlánok T1 a T6 mal hĺbku 10 mm od exponovanej strany, T2 a T7 20 mm, T3 a T8 40 mm, T4 a T9 60 mm, T5 a T10 80 mm. Na zaznamenávanie teplôt sa použil AHLBORN ALMEMO 2290-8710 V7 (Ahlborn Messund Regelungstechnik GmbH, Holzkirchen, Germ). Skúšobné vzorky boli zaťažené radiačným panelom umiestneným 100 mm od skúšobnej vzorky. Veľkosť radiačnej plochy bola 480 × 280 mm. Zdrojom energie keramického sálacieho panelu bol plynný propán-bután s konštantným prietokom 15 m³∙h⁻¹ s výkonom 50 kW.

Model konečných prvkov

Model konečných prvkov (FEM) bol zjednodušený na proces prenosu tepla materiálom pomocou nestacionárnej teplotnej analýzy [29, 30, 46–50] pomocou softvéru ANSYS 2024/R² (ANSYS, Inc., Canonsburg, Pennsylvania, USA). Na definovanie vzťahu medzi tepelným tokom a teplotou softvér ANSYS používa Fourierov zákon (rov. 5), kde 𝑞 je tepelný tok, ∇𝑇 je teplotný gradient a 𝑘 je tepelná vodivosť, ktorá predstavuje schopnosť materiálu prenášať teplo. V podmienkach ustáleného stavu je tepelná vodivosť definovaná ako tepelný tok prenášaný materiálom v dôsledku jednotkového teplotného gradientu. Pretože vlastnosti drevených materiálov sa menia s teplotou, upravuje sa Fourierov zákon v jednorozmernom priestore, kde tepelná vodivosť k je funkciou teploty T (rov. 6). Rovnice 5–6 nezahŕňajú čas na riešenie problémov prenosu tepla. Na riešenie zložitej 2D alebo 3D geometrie softvér ANSYS používa Newton-Raphsonovu metódu.

(5)

(6)

Hlavnou rovnicou pre nestacionárne vedenie tepla cez pevnú látku je rovnica tepelnej rovnováhy (rovnica 7–8).

(7)

(8)

kde je

ρ: hustota materiálu,
c: hmotnostná tepelná kapacita,
k: tepelná vodivosť,
q: tepelný tok,
T: termodynamická teplota.

Modelovanie správania sa drevených konštrukčných prvkov zaťažených požiarom v softvéry Ansys

Obr. 3 Sieť konečných prvkov

FEM bol vytvorený v prostredí „SpaceClaim“ (ANSYS, Inc., Canonsburg, Pennsylvania, USA) a bol zjednodušený na jednoduchú kocku s rozmerom hrany 100 mm a otvormi pre termočlánky. Keďže drevený nosník sa ohrieval rovnomerne na jednu jeho stranu, prenos tepla kolmo na vlákna bol dominantný. Bola preto použitá izotropná tepelná vodivosť. Pre drevený nosník bola vytvorená štvorstenná sieť s veľkosťou elementu 2,5 mm, pre radiačný panel bola vytvorená šesťstenná sieť s veľkosťou elementu 2,5 mm (obr. 3). V oblastiach otvorov bola použitá funkcia „Inflation“ na vytvorenie jemnejšej siete. Celkovo sa vygenerovalo 584 632 prvkov a 875 960 uzlov.

Tepelný most medzi nosníkom a radiačným panelom bol vytvorený manuálne pomocou kontaktného regiónu. Okrajové podmienky boli nastavené v zhode s reálnymi strednorozmerovými skúškami. Teploty zo simulácií boli zaznamenané funkciou „Priemerná teplota“ vo vopred definovaných polohách v otvoroch, ako sa to používalo pri realizovaných požiarnych skúškach. Výpočet bol rozdelený na 60 podkrokov s dĺžkou trvania 30 s a maximálnym počtom iterácií 1 000.

Verifikácia modelu

Verifikácia pripraveného FEM bola vykonaná pomocou porovnania teplotných priebehov nameraných termočlánkami pri reálnych skúškach a výsledkami z modelovania. Kľúčovou úlohou bolo dosiahnuť čo najvyššiu presnosť počítačového modelu. Pre vyjadrenie presnosti modelu bol použitý koeficient spoľahlivosti R².

Implementácia vstupných údajov o materiálových charakteristikách

Do vytvoreného modelu boli vložené materiálové charakteristiky dreva v kombinácii hustota, tepelná vodivosť a entalpia. Všetky vlastnosti boli závislé od teploty. Hustota dreva bola prepočítaná na základe Eurokódu 5 [9]. Počiatočná hustota dreva bola zadaná na základe výsledkov meraní hustoty pomocou gravimetrickej metódy. V prípade tepelnej vodivosti dreva bolo použitých niekoľko nastavení. Počiatočná krivka tepelnej vodivosti vychádzala z Eurokódu 5 [9], ktorá bola postupne upravovaná podľa Çavuşa a kol. [15], pri teplote fázovej zmeny vody boli vyskúšané nastavenia podľa Chena [39] a Mathura a kol. [40]. Teploty, pri ktorých dochádza k fázovej premene vody v dreve, boli zistené zo získaných teplotných kriviek zo strednorozmerových skúšok pomocou T-history metódy podľa Zhanga a kol. [37]. Na tento účel bol použitý softvér MATLAB R2023b (The MathWorks, Inc., Natick, Massachusetts, USA). Entalpia bola rátaná pomocou špecifického tepla podľa Nasera [5].

Výsledky

Priemerná vlhkosť dreva bola pomocou gravimetrickej metódy stanovená na hodnotu 9,54 % so smerodajnou odchýlkou 0,23 %. Priemerná hustota dreva pri nulovej vlhkosti bola stanovená na hodnotu 387,37 kg·m⁻³ so smerodajnou odchýlkou 11,91 kg·m⁻³. Pri vlhkosti 9,54 % bola priemerná hustota dreva stanovená na hodnotu 424,33 kg·m⁻³ so smerodajnou odchýlkou 13,89 kg·m⁻³.

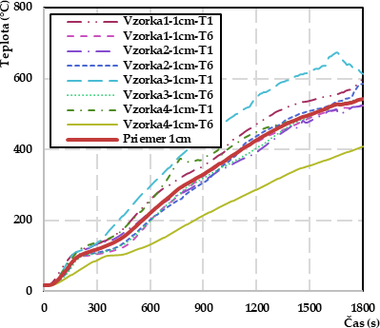
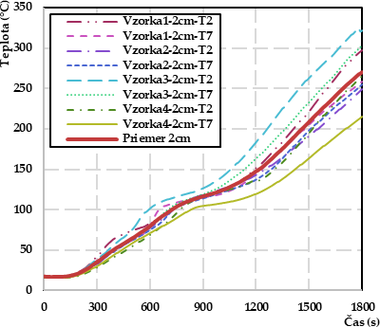
Výsledky zo strednorozmerových testov drevených nosníkov boli spracované vo forme grafov (obr. 4). V hĺbke 1 cm bola priemerná smerodajná odchýlka 53,4 °C a v hĺbke 2 cm 14,6 °C.

Obr. 4 Porovnanie teplotno-časových kriviek: b) hĺbka 2 cm

Obr. 4 Porovnanie teplotno-časových kriviek a) hĺbka 1 cm, b) hĺbka 2 cm

Uvedené sú len grafy pre hĺbku 1 cm a 2 cm, pretože z teplotných priebehov bolo viditeľné, že iba v hĺbke 1 a 2 cm došlo k fázovej zmene vody obsiahnutej v dreve (dosiahnutie teploty minimálne 100 °C). Tieto teplotné krivky boli použité pri zistení začiatku a konca fázovej premeny podľa T-history metódy [37]. Priemerné hodnoty „Priemer 1 cm“ a „Priemer 2 cm“ boli v softvéry MATLAB upravené pomocou aplikácie „Data Cleaner“ a funkcie „Smooth Data“. Cieľom bolo vyhladiť krivky, aby bolo možné určiť inflexné body, minimum druhej derivácie a maximum prvej derivácie.

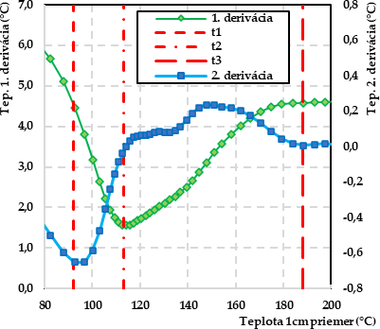
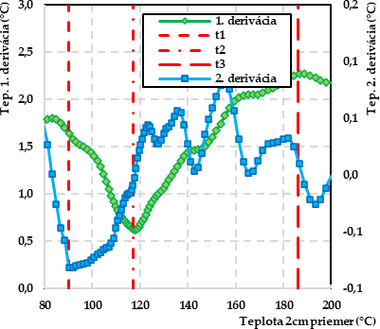
Následne boli vyhotovené krivky prvej a druhej derivácie pre teplotné profily v hĺbke 1 a 2 cm, z ktorých boli pomocou softvéru MATLAB zistené minimum druhej derivácie (t₁), inflexný bod (t₂) a maximum prvej derivácie (t₃). Pre teplotný profil v hĺbke 1 cm bolo t₁ 92,5 °C, t₂ 112,6 °C a t₃ 188,5 °C (obr. 5a). Pre teplotný profil v hĺbke 2 cm bolo t₁ 90,1 °C, t₂ 117,0 °C a t₃ 186,7 °C (obr. 5b).

Obr. 5 Krivky prvej a druhej derivácie: b) Priemer 2 cm

Obr. 5 Krivky prvej a druhej derivácie: a) Priemer 1 cm, b) Priemer 2 cm

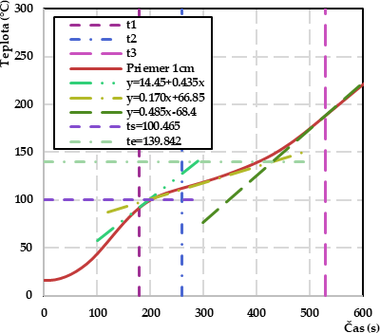
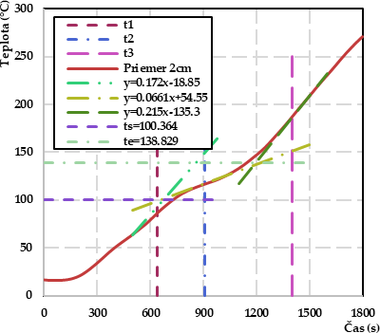
Pre uvedené body boli vygenerované dotyčnice bodov. Pomocou priesečníkov dotyčníc boli stanovené teploty začiatku a konca fázovej premeny. Pre hĺbku 1 cm boli hodnoty stanovené na 100,4 °C a 139,8 °C (obr. 6a). Pre hĺbku 2 cm boli hodnoty stanovené na 100,4 °C a 138,8 °C (obr. 6b). Priemerné hodnoty 100,4 °C a 139,3 °C boli použité pri úprave vstupných hodnôt počítačového modelu.

Obr. 6 Stanovenie počiatočného a koncového bodu fázovej zmeny vody v dreve: b) Priemer 2 cm

Obr. 6 Stanovenie počiatočného a koncového bodu fázovej zmeny vody v dreve: a) Priemer 1 cm, b) Priemer 2 cm

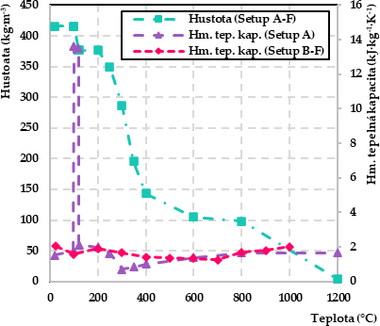
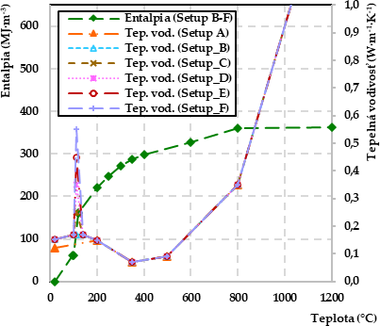
Následne boli do modelu implementované materiálové charakteristiky o tepelnej vodivosti, hustote a entalpii (obr. 7). Bolo vyskúšaných 6 rôznych nastavení A–F. Počiatočné nastavenie A vychádzalo z Eurokódu 5 [9]. V nastaveniach B–F bola použitá entalpia, ktorej hodnoty boli počítané pomocou hmotnostnej tepelnej kapacity podľa Nasera [5]. V nastaveniach B–F boli vykonané úpravy tepelnej vodivosti dreva, pretože v tomto smere existuje najväčší rozptyl nameraných údajov v dostupnej literatúre. Ako prvá bola upravená počiatočná tepelná vodivosť dreva pri teplote 20 °C a vlhkosti 9,54 % podľa vzorca (1, 2) na hodnotu 0,153 W·m⁻¹·K⁻¹. Viacerí autori [1–5, 7–12] uvádzajú, že s rastúcou teplotou sa hodnota tepelnej vodivosti zvyšuje lineárne v priemere o približne 0,015 W·m⁻¹·K⁻¹ pri 100 °C [1–5, 7–12]. Preto tepelná vodivosť bola pri teplote 100 °C nastavená na 0,168 W·m⁻¹·K⁻¹. V oblasti fázovej premeny boli testované rôzne nastavenia (B–F) tepelnej vodivosti. Postupne boli menené maximá tepelnej vodivosti (0,168, 0,25, 0,35, 0,45 a 0,55 W·m⁻¹·K⁻¹) v oblasti inflexného bodu, ktorý sa nachádzal v priemere pri teplote 114,8 °C. Hodnoty úbytku na hustote boli definované podľa Eurokódu 5 [9]. Graf entalpie bol vytvorený pomocou rovníc (rov. 9–11).

(9)

(10)

(11)

kde je

H_T₀: počiatočný bod krivky entalpie a je rovný 0,
c_sd: tepelná kapacita suchého dreva podľa Nasera [5],
ρ_sd: hustota suchého dreva,
c_v: tepelná kapacity vody (4,22 kJ·kg⁻¹·K⁻¹),
ρ_v: hustota vody,
w: obsah vody v dreve.

Rovnica (9) reprezentuje výpočet entalpie suchého dreva a vody obsiahnutej v dreve za teploty T₁. Rovnica (10) reprezentuje výpočet entalpie v oblasti fázovej premeny vody pri teplote T₂, H_výp je výparná entalpia (2257 kJ·kg⁻¹). Rovnica (11) reprezentuje výpočet entalpie suchého dreva za teploty T₃.

Obr. 7 Vstupné údaje (hustota, tepelná kapacita, entalpia a tepelná vodivosť) v procese tvorby počítačového modelu: b) entalpia a tepelná vodivosť

Obr. 7 Vstupné údaje (hustota, tepelná kapacita, entalpia a tepelná vodivosť) v procese tvorby počítačového modelu: a) hustota a tepelná vodivosť, b) entalpia a tepelná vodivosť

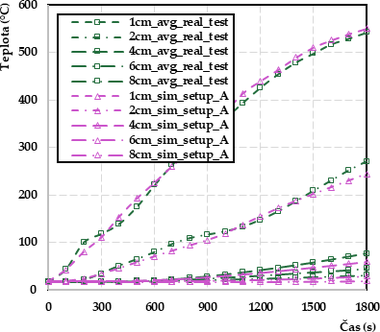
Po skončení simulácií s rôznymi nastaveniami materiálových vlastností boli výsledné hodnoty získané zo simulácií porovnané so strednorozmerovými testami (obr. 8). Presnosť simulácií bola stanovená pomocou koeficientu spoľahlivosti (R²) v softvéri MATLAB.

Obr. 8 Odlišné nastavenia materiálových charakteristík počítačového modelu a ich vplyv na výsledky: a) nastavenie A podľa Eurokódu 5

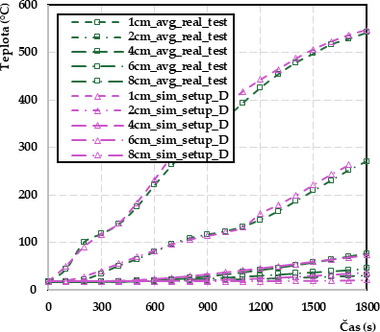
Obr. 8 Odlišné nastavenia materiálových charakteristík počítačového modelu a ich vplyv na výsledky: b) nastavenie D s upravenou tepelnou vodivosťou s maximom 0,45 W·m⁻¹·K⁻¹ pri 114,8 °C

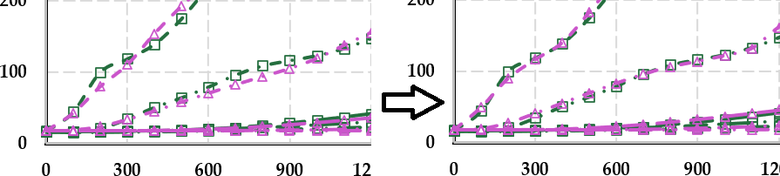
Obr. 8 Odlišné nastavenia materiálových charakteristík počítačového modelu a ich vplyv na výsledky: c) spresnenie výsledkov v oblasti fázovej zmeny vody z nastavenia A na nastavenie D

Obr. 8 Odlišné nastavenia materiálových charakteristík počítačového modelu a ich vplyv na výsledky: a) nastavenie A podľa Eurokódu 5, b) nastavenie D s upravenou tepelnou vodivosťou s maximom 0,45 W·m⁻¹·K⁻¹ pri 114,8 °C, c) spresnenie výsledkov v oblasti fázovej zmeny vody z nastavenia A na nastavenie D

Z výsledkov simulácií je postupne vidieť význam úprav vstupných údajov. S nastavením A výsledky modelovania neodzrkadľujú fázovú zmenu začínajúcu pri teplote 100 °C (obr. 8a). R² pre nastavenie A bola 0,98257. V prípade nastavenia B zvýšenie počiatočnej tepelnej vodivosti a využitie entalpie spresnilo výsledky modelovania na hodnotu R² 0,98444. Pri teplote 100 °C bol viditeľný mierny zlom reprezentujúci fázovú zmenu, avšak len s využitím entalpie výsledky modelovania neukázali dobrý priebeh teplôt v oblasti fázovej zmeny. S nastavením C došlo k ďalšiemu spresneniu výsledkov simulácie a k zväčšeniu zlomu teplotnej krivky pri teplote 100 °C, R² bolo 0,98622. Nastavenie D prinieslo ďalšie spresnenie výsledkov s R² 0,98691 a zvýraznenie zlomu teplotnej krivky pri začiatku fázovej zmeny (obr. 8b). Vďaka nastaveniu E a F došlo k ešte výraznejšiemu zlomu pri teplote 100 °C, R² bolo menšie a malo hodnotu 0,98664 respektíve 0,98588. Uvedené hodnoty R² predstavovali priemerné R² zo všetkých hĺbok pre každé nastavenie (A–F).

Nastavenie A prinieslo najmenšiu presnosť so smerodajnou odchýlkou 0,0028. Nastavenie B malo smerodajnú odchýlku 0,0063, C 0,0052, D 0,0030, E 0,0014 a G 0,0032. Z grafu je viditeľné, že nastavenie D dosahuje najvyššiu presnosť, hodnoty majú v porovnaní s ostatnými priemerný rozptyl, čo potvrdzuje aj smerodajná odchýlka. Nastavenia D a E už prinášajú nižšiu presnosť. Z výsledkov tým pádom vyplýva, že najpresnejšie výsledky simulácie prinieslo nastavenie D s hodnotou tepelnej vodivosti 0,45 W·m⁻¹·K⁻¹ pri teplote 114,8 °C s presnosťou 98,691 %.

Diskusia

Z výsledkov je viditeľné, že úprava vstupných nastavení materiálových charakteristík dreva prináša signifikantný posun v presnosti výsledkov. Nastavenia podľa Eurokódu 5 [9] poskytujú spoľahlivé výsledky s relatívne dobrou presnosťou, avšak ich využitie v prípade rôznej vlhkosti dreva je obmedzené, pretože vstupné údaje o špecifickom teple a tepelnej vodivosti neberú vlhkosť dreva do úvahy [30]. Zle nastavené vstupné údaje môžu viesť k vysokému rozptylu výsledných hodnôt, čo potvrdzuje aj Naser [5] a Molina a kol. [41].

Ako najzložitejší problém sa ukazuje správne napodobnenie teplotného priebehu v oblasti fázovej zmeny vody. Výsledky modelovania od Regueira a Guaita [42] ukázali, že sa im tento priebeh podarilo napodobniť len čiastočne, zatiaľ čo výsledky Martíneza a kol. [43] túto oblasť nesimulovali vôbec. Couto a kol. [44] využili strednorozmerové požiarne skúšky a FEA pre výskum požiarnej odolnosti drevených dosiek a zistili, že množstvo odchýlok medzi reálnymi testami a výsledkami z počítačového modelovania sú zapríčinené práve vlhkosťou dreva. S využitím entalpie je možné do určitej mieri napodobniť fázovú premenu vody v dreve pri teplote 100 °C [23, 30, 31], čo potvrdili aj výsledky simulácií. Avšak len s pomocou entalpie je presnosť simulácií počas fázovej zmeny vody relatívne priemerná.

T-history metóda [37] sa ukázala ako užitočný nástroj, pomocou ktorého sa presnosť simulácií vysoko spresnila. Umožnila presnejšie definovať začiatok a koniec fázovej premeny, ktorý striktne udáva Eurokód 5 [9], ale aj mnoho ďalších autorov [7, 33–36]. Ďalšie spresnenie výsledkov prinieslo zvýšenie tepelnej vodivosti dreva podľa hustoty a obsahu vlhkosti v oblasti pred fázovou zmenou vody [15, 23]. V oblasti fázovej premeny vody sa ukázalo nastavenie D s hodnotou tepelnej vodivosti 0,35 W·m⁻¹·K⁻¹ pri teplote 114,8 °C ako najlepšie s presnosťou 98,691 % s takmer dokonalým napodobnením teplotného priebehu počas fázovej premeny vody. Dôvod, prečo zmenou tepelnej vodivosti bol napodobnený priebeh teplôt v oblasti fázovej premeny, je vo vzorcoch, ktoré FEA využívajú. Pokiaľ zmenou vlastností ako entalpia, špecifické teplo alebo hustota dreva nenastane zmena teplotného priebehu, poslednou vlastnosťou, ktorou je možné efekt fázovej premeny napodobniť, je tepelná vodivosť, čo potvrdzujú aj výsledky autorov skúmajúcich fázové premeny materiálov [39, 40]. Z výsledkov simulácií ďalej vyplýva, že by mohla existovať korelácia medzi obsahom vlhkosti dreva a maximálnou hodnotou tepelnej vodivosti dreva v oblasti fázovej premeny vody.

Záver

Nastavenia podľa Eurokódu 5 poskytujú spoľahlivé výsledky s relatívne dobrou presnosťou, avšak ich využitie v prípade rôznej vlhkosti dreva je obmedzené.
S využitím entalpie je možné do určitej mieri napodobniť fázovú premenu vody v dreve pri teplote 100 °C. Avšak len s pomocou entalpie je presnosť simulácií počas fázovej zmeny relatívne priemerná.
T-history metóda predstavuje užitočný nástroj, pomocou ktorého sa presnosť simulácií vysoko spresnila.
V oblasti fázovej premeny vody sa ukázalo nastavenie s hodnotou tepelnej vodivosti 0,45 W·m⁻¹·K⁻¹ pri teplote 114,8 °C ako najlepšie s presnosťou 98,691 % s takmer dokonalým napodobnením teplotného priebehu počas fázovej premeny vody.
Z výsledkov simulácií vyplýva, že by mohla existovať korelácia medzi obsahom vlhkosti dreva a maximálnou hodnotou tepelnej vodivosti dreva v oblasti fázovej premeny vody.

Financovanie

Táto práca bola podporená Agentúrou na podporu výskumu a vývoja na základe Zmluvy č. APVV-22-0030.

Zdroje

Wald, F., et al., Modelování dynamiky požáru v budovách. 2017: České vysoké učení technické v Praze.
Hu, Y.P., et al., Experimental Study of the Anisotropic Thermal Conductivity of Spruce Wood. International Journal of Thermophysics, 2023. 44(8). https://doi.org/10.1007/s10765-023-03238-7.
Malaga-Tobola, U., et al., Influence of wood anisotropy on its mechanical properties in relation to the scale effect. International Agrophysics, 2019. 33(3): p. 337-345. https://doi.org/10.31545/intagr/110808.
Bartlett, A.I., R.M. Hadden, and L.A. Bisby, A Review of Factors Affecting the Burning Behaviour of Wood for Application to Tall Timber Construction. Fire Technology, 2019. 55(1): p. 1-49. https://doi.org/10.1007/s10694-018-0787-y.
Naser, M.Z., Properties and material models for common construction materials at elevated temperatures. Construction and Building Materials, 2019. 215: p. 192-206. https://doi.org/10.1016/j.conbuildmat.2019.04.182.
Maraveas, C., et al., Performance of Timber Connections Exposed to Fire: A Review. Fire Technology, 2015. 51(6): p. 1401-1432. https://doi.org/10.1007/s10694-013-0369-y.
Frangi, A., Brandverhalten von Holz-Beton-Verbunddecken. 2001, Birkhäuser.
Janssens, M.L. and R.H. White, Short communication: Temperature profiles in wood members exposed to fire. Fire and Materials, 1994. 18(4): p. 263-265. https://doi.org/10.1002/fam.810180410.
European Committee for, S. and I. British Standards, Eurocode 5 : design of timber structure. 1994, Brussels: BSI Brussels.
Kmiecik, K., Impact of wood species on the timber beam strength and stiffness under fire. IOP Conference Series: Materials Science and Engineering, 2019. 586(1): p. 012004. https://doi.org/10.1088/1757-899X/586/1/012004.
Kamenická, Z., et al., METHODS FOR DETERMINING THE CHARRING RATE OF TIMBER AND THEIR MUTUAL COMPARISON. Wood Research, 2018. 63(4): p. 583-590.
Maciulaitis, R., A. Jefimovas, and P. Zdanevicius, RESEARCH OF NATURAL WOOD COMBUSTION AND CHARRING PROCESSES. Journal of Civil Engineering and Management, 2012. 18(5): p. 631-641.
https://doi.org/10.3846/13923730.2012.720935.
Friquin, K.L., Material properties and external factors influencing the charring rate of solid wood and glue-laminated timber. Fire and Materials, 2011. 35(5): p. ;303-327. https://doi.org/10.1002/fam.1055.
Peng, L., et al., Predicting the Fire Resistance of Wood–Steel–Wood Timber Connections. Fire Technology, 2011. 47(4): p. 1101-1119. https://doi.org/10.1007/s10694-009-0118-4.
Çavus, V., et al., Determination of Thermal Conductivity Properties in Some Wood Species Obtained from Turkey. Bioresources, 2019. 14(3): p. 6709-6715. https://doi.org/10.15376/biores.14.3.6709-6715.
Jang, E.S. and C.W. Kang, THE RELATIONSHIP BETWEEN BULK DENSITY AND THERMAL CONDUCTIVITY IN VARIOUS KOREAN WOODS. Wood Research, 2022. 67(2): p. 178-186. https://doi.org/10.37763/wr.1336-4561/67.2.178186.
Amel, L., et al., Experimental thermal characterization of bio-based materials (Aleppo Pine wood, cork and their composites) for building insulation. Energy and Buildings, 2016. 116. https://doi.org/10.1016/j.enbuild.2016.01.007.
Kristák, L., R. Igaz, and I. Ruziak, Applying the EDPS Method to the Research into Thermophysical Properties of Solid Wood of Coniferous Trees. Advances in Materials Science and Engineering, 2019. 2019.
https://doi.org/10.1155/2019/2303720.
Acuña-Alegri, L., et al., Inverse determination of thermal conductivity in wood of Pinus rathata. Maderas-Ciencia Y Tecnologia, 2018. 20(4): p. 595-610. https://doi.org/10.4067/s0718-221x2018005004701.
Vololonirina, O., M. Coutand, and B. Perrin, Characterization of hygrothermal properties of wood-based products - Impact of moisture content and temperature. Construction and Building Materials, 2014. 63: p. 223-233.
https://doi.org/10.1016/j.conbuildmat.2014.04.014.
Mvondo, R.R.N., et al., Influence of moisture content on the thermophysical properties of tropical wood species. Heat and Mass Transfer, 2020. 56(4): p. 1365-1378. https://doi.org/10.1007/s00231-019-02795-8.
Zvicevicius, E., et al. INFLUENCE OF MOISTURE ON OSIER WILLOW CHOPS CHARACTERISTICS. in 18th International Scientific Conference on Engineering for Rural Development (ERD). 2019. Jelgava, LATVIA.
Špilák D., M.A., Kačíková D., Progressive Methods for Determining the Fire Resistance of Wooden Beams 2022: Aleš Čeněk. 162.
Cachim, P.B. and J.-M. Franssen, Assessment of Eurocode 5 Charring Rate Calculation Methods. Fire Technology, 2010. 46(1): p. 169-181. https://doi.org/10.1007/s10694-009-0092-x.
Cachim, P.B. and J.-M. Franssen, Comparison between the charring rate model and the conductive model of Eurocode 5. Fire and Materials, 2009. 33(3): p. 129-143. https://doi.org/10.1002/fam.985.
Rinta-Paavola, A., D. Sukhomlinov, and S. Hostikka, Modelling Charring and Burning of Spruce and Pine Woods During Pyrolysis, Smoldering and Flaming. Fire Technology, 2023. 59(5): p. 2751-2786.
https://doi.org/10.1007/s10694-023-01458-9.
Pecenko, R., S. Svensson, and T. Hozjan, Modelling heat and moisture transfer in timber exposed to fire. International Journal of Heat and Mass Transfer, 2015. 87: p. 598-605. https://doi.org/10.1016/j.ijheatmasstransfer.2015.04.024.
Richter, F. and G. Rein, A multiscale model of wood pyrolysis in fire to study the roles of chemistry and heat transfer at the mesoscale. Combustion and Flame, 2020. 216: p. 316-325. https://doi.org/10.1016/j.combustflame.2020.02.029.
Reszka, P. and J.L. Torero, In-depth temperature measurements in wood exposed to intense radiant energy. Experimental Thermal and Fluid Science, 2008. 32(7): p. 1405-1411.
https://doi.org/10.1016/j.expthermflusci.2007.11.014.
Spilák, D. and A. Majlingová, Progressive Methods in Studying the Charred Layer Parameters Change in Relation to Wood Moisture Content. Polymers, 2022. 14(22). https://doi.org/10.3390/polym14224997.
Spilák, D., et al., Determining the Charred Layer of Wooden Beams with Finite Element Analysis Based on Enthalpy Approach. Buildings, 2022. 12(7). https://doi.org/10.3390/buildings12070875.
Shen, D.K., et al., Modeling pyrolysis of wet wood under external heat flux. Fire Safety Journal, 2007. 42(3): p. 210-217. https://doi.org/10.1016/j.firesaf.2006.09.001.
Fuller, J.J., R.J. Leichti, and R.H. White, Temperature distribution in a nailed gypsum-stud joint exposed to fire. Fire and Materials, 1992. 16(2): p. 95-99. https://doi.org/10.1002/fam.810160206.
König, J., Timber frame assemblies exposed to standard and parametric fires. Part 2 A design model for standard fire exposure. 2000.
Fredlund, B. A model for heat and mass transfer in timber structures during fire: a theoretical, numerical and experimental study. 1988.
Mehaffey, J.R., P. Cuerrier, and G. Carisse, A model for predicting heat transfer through gypsum-board/wood-stud walls exposed to fire. Fire and Materials, 1994. 18(5): p. 297-305. https://doi.org/https://doi.org/10.1002/fam.810180505.
Zhang, Y.Y.C., et al., Derivation of thermal properties of phase change materials based on T-history method. Journal of Energy Storage, 2020. 27. https://doi.org/10.1016/j.est.2019.101062.
Bie, Y., et al., Effect of phase transition temperature and thermal conductivity on the performance of Latent Heat Storage System. Applied Thermal Engineering, 2018. 135: p. 218-227.
https://doi.org/10.1016/j.applthermaleng.2018.02.036.
Chen, H.Y., et al., Thermal Conductivity during Phase Transitions. Advanced Materials, 2019. 31(6).
https://doi.org/10.1002/adma.201806518.
Mathur, V., P.K. Arya, and K. Sharma. Estimation of activation energy of phase transition of PVC through thermal conductivity and viscosity analysis. in International Conference on Innovations in Technology, Management and Design for Achieving Sustainable Development Goals - Materials Science (ICSDG). 2020. Jaipur, INDIA.
Molina, J., et al., Análise Numérica do Comportamento de Elementos de Madeira em Situação de Incêndio. Floresta e Ambiente, 2012. 19: p. 162-170. https://doi.org/10.4322/floram.2012.019.
Regueira, R. and M. Guaita, Numerical simulation of the fire behaviour of timber dovetail connections. Fire Safety Journal, 2018. 96: p. 1-12. https://doi.org/10.1016/j.firesaf.2017.12.005.
Martinez, J., et al., Study of the influence of heat transfer of a CLT beam through FEM. Journal of Physics: Conference Series, 2018. 1107: p. 032003. https://doi.org/10.1088/1742-6596/1107/3/032003.
Couto, D.L.P., et al., Perforated cellular wooden slabs under fire: Numerical and experimental approaches. Journal of Building Engineering, 2016. 8: p. 218-224. https://doi.org/10.1016/j.jobe.2016.10.007.

Komentář recenzenta Ing. Jakub Šejna, Ph.D., ČVUT v Praze, pracoviště UCEEB

Článek se zabývá klíčovým problémem počítačových simulací založených na metodě konečných prvků (FEA) – přesností vstupních dat. Autoři zkoumají, jak zásadní vliv mají materiálové vlastnosti, jako je tepelná vodivost, hmotnostní tepelná kapacita, hustota a entalpie, na výsledky simulací. Cílem článku je nejen upozornit na nedostatky v dosavadních metodikách, ale také navrhnout způsoby, jak lze přesnost modelů zlepšit. Metodika zahrnovala požární zkoušky dřevěných nosníků smrkového dřeva, jejichž výsledky byly následně validovány pomocí počítačových simulací v softwaru ANSYS. Studie zdůrazňuje význam správného nastavení tepelných parametrů materiálu, přičemž upozorňuje na specifické výzvy spojené s vlhkostí dřeva a fázovými změnami vody při teplotě kolem 100 °C. Z výsledků vyplývá, že zavedení metodiky T-history a přesnější nastavení tepelné vodivosti vedly k výraznému zvýšení přesnosti modelu – až na 98,691 %. K článku jsme vypracovali celou řadu poznámek a doporučení, která byla autorem vesměs akceptována. Doporučuji k vydání.