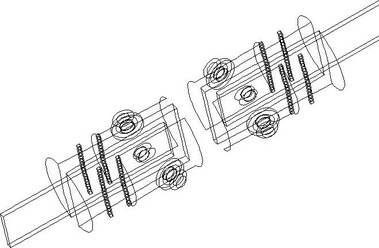
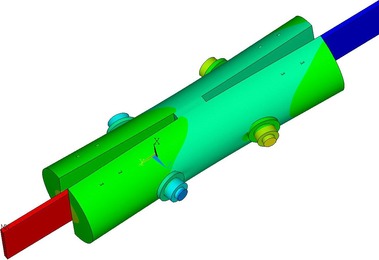
Několik typů zesílení taženého ocelového spoje dřevěné kulatiny
Příspěvek se zabývá analýzou taženého ocelového spoje dřevěné kulatiny, pro který je navrženo několik typů zesílení. Navržené typy zesílení jsou laboratorně testovány na celkovou únosnost. Souběžně s laboratorními zkouškami je provedeno numerické modelování, které se zaměřilo zejména na tuhost spoje v průběhu zatěžování s vlivem fyzikální a geometrické nelinearity. Numerické výpočty jsou provedeny metodou konečných prvků s využitím prostorových výpočetních modelů.
Úvod
Dřevostavby nebo konstrukční prvky ze dřeva patří k moderním prvkům architektury. Současně je jim také věnována velká pozornost ve výzkumu [10]. Dřevo se také často kombinuje s dalšími materiály [1] a [4]. Při návrhu dřevěných konstrukcí je zejména vhodné věnovat pozornost řešení konstrukčním detailům [6] a [9]. Podstatné je také určení materiálových vlastností dřeva [5]. Návrh dřevěných konstrukcí se řídí normovými postupy [2] a [3]. Existuje však také celá řada publikací, které uvádějí podrobnější postupy návrhu a posudků dřevěných konstrukcí [7], [8] a [15]. V některých případech je také vhodné použít pravděpodobnostního přístupu, např. [11]. Pro výpočet vnitřních sil prutových prvků a konstrukcí se využívá nejčastěji softwaru založeného na metodě konečných prvků. Mezi běžně používané standardní software patří SCIA Engineer [14] nebo pro pokročilé analýzy ANSYS [13]. Pro technickou praxi není ANSYS vzhledem k obecnosti, kterou nabízí, příliš efektivní. Tento software nebyl vytvořen pro standardní normové návrhové postupy.
Pro analýzu a optimalizaci je zvolen ocelový spoj dřevěné kulatiny. K uvedenému spoji jsou publikovány výsledky z laboratorního testovaní v [12]. Spoj je používán u srubových staveb a vyskytuje se také často na konstrukcích v lesním hospodářství, u rozhleden nebo příhradových mostů a lávek. Použití tohoto typu spoje v mostním stavitelství a rozhlednách vede k jeho dynamickému namáhání, které je nutné také vhodně zohlednit při návrhu. Mezi další podstatné vlivy na únosnost a chování spoje patří působení přírodních vlivů a kvalita údržby. Z těchto důvodů bylo pro optimalizaci chování a únosnosti spoje navrženo několik typů zesílení. Jednotlivé typy zesílení byly následně testovány v laboratoři, numericky modelovány a navzájem porovnávány. Předložený článek shrnuje dosažené výsledky. Numerické modelování se zaměřilo na tuhost spoje v průběhu zatěžování s vlivem fyzikální a geometrické nelinearity. Dosažené výsledky z numerického modelování mohou být dále použity pro návrh přilehlých segmentů tvořících konstrukční celek spoje.
Řešení detailu spoje
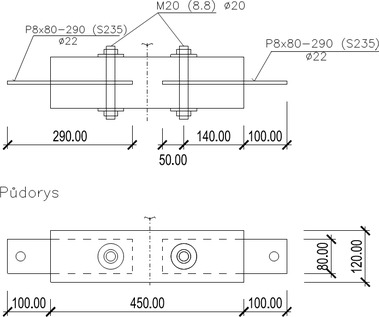
Detail spoje bez zesílení je vidět na Obr. 1. Jedná se o spojení dřevěné kulatiny s vnitřním ocelovým plechem, kde spoj je tvořen ocelovými svorníky. Dřevo je třídy řeziva C24 a ocel tvoří ocelová plotna o síle 8 mm třídy S235. Svorníky jsou průměru 20 mm třídy oceli 8.8. Dřevěná část je tvořena přírodní kulatinou průměru 120 mm se suky a přírodními imperfekcemi a výsušnými trhlinami. Ocel je bez povrchové úpravy.
K testovacímu zařízení byl spoj přichycen pomocí dvou svorníků průměru 20 mm třídy oceli 8.8, nebo přes ocelovou plotnu na třecí spoj do čelistí lisu. Spoj byl testován na více pracovištích (ČVUT PRAHA, VŠB-TU OSTRAVA FAST, VÚD ŽILINA). Spoje byly dotaženy. Vývrt ve dřevě byl průměru 20 mm a v oceli 22 mm. Šrouby byly průměru 20 mm třídy 8.8.
Spoj byl u zkoušky v laboratoři zatížen posunem hlavy lisu. V numerickém modelu byl spoj zatěžován pouze deformačně a staticky. Dynamicky zatížený spoj v reálném testu nebyl numericky modelován. V numerickém modelu bylo zatížení vnášeno jako deformační na dráze 4 mm. Okrajové podmínky jsou nastaveny tak, aby odpovídaly co nejvíce reálnému upnutí v lisu. Jeden konec ocelové vnitřní desky je na svém okraji fixován ve všech třech směrech pohybu a druhý konec je fixován pouze v kolmých směrech na ocelový vnitřní plát. Směr rovnoběžný s osou kulatiny a ocelové plotny je ponechán volně předepsanému posunu 4 mm (posun vyvozuje tahové namáhání spoje).
Na Obr. 1 je vidět technický nákres a popis spoje kulatiny tak, jak byl proveden pro laboratorní zkoušky a numerický model. Na tomto schématu je spoj bez zesílení prvky pro směr kolmo na vlákna dřeva. Základní dělení vyrobených a modelovaných spojů kulatiny se dělí na tři typy:
1) typ TSK 1 – jde o nezesílený spoj, viz Obr. 1
Jedná se o nezesílený spoj (Obr. 1), kdy může volně docházet k rozštípání dřeva kolmo na vlákna. Tento spoj je snadno proveditelný, ale v oblastech blízkých k plné únosnosti se může v porušení chovat křehce – vykazuje malou duktilitu. Dochází zde při statickém zatížení k náhlému porušení vzorku bez velkých plastických deformací spoje.
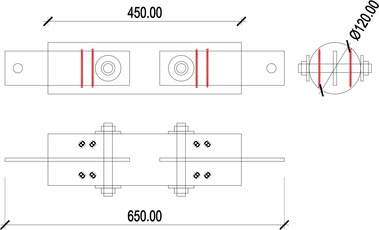
2) typ TSK 2 – jde o zesílený spoj pomocí vrutů se závitem po celé délce dříku, viz Obr. 2
Jedná se o zesílený spoj vruty bez předvrtání se závitem po celé délce dříku zapuštěnými kolmo na vlákna, viz schéma na Obr. 2. Tento spoj je také pro provedení rychlý a dostupný. Pomocí tohoto zesílení je možné zvýšit duktilitu spoje a zvýšit únosnost spoje. Sice zde také dojde pro extrémní zatížení k rozpraskání kolmo na vlákna, ale spoj není zcela rozštípán, protože ho drží vruty a může dále přenášet zatížení. Tento spoj může mít čtyři základní typy porušení: a) vytržení vrutů a poté rozštípání dřeva b) blokový smyk c) přetržení dřevěného prvku d) zplastizování ocelových prvků nebo otlačení stěny dřeva v oblasti spoje.
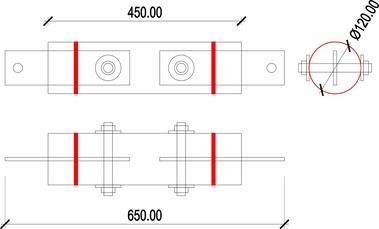
3) typ TSK 3 – jde o typ zesílený pomocí ocelového pásu viz Obr. 3
Jedná se o zesílený spoj s ocelovou objímkou kolem kulatiny Obr. 3. Tento spoj je také snadno proveditelný a dostupný. Pomocí tohoto zesílení je možné zvýšit duktilitu spoje a zvýšit únosnost spoje. Tento spoj může mít čtyři základní typy porušení a) zplastizování a přetržení objímky b) blokový smyk c) přetržení dřevěného prvku d) zplastizování ocelových prvků nebo stěny dřeva v oblasti spoje. Ocelové objímky jsou u spoje dotaženy před zkouškami v laboratoři, ale nepředpokládá u nich předepnutí.
Vyhodnocení laboratorních zkoušek a numerických modelů
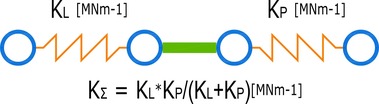
Celková únosnost taženého spoje s jedním svorníkem se vypočte ze vztahů (1) až (3), kdy pro analyzovaný svorník je únosnost pro dva střihy přibližně 46,5 kN a tuhost přibližně 15,4 MNm−1 podle DIN 1052 [2]. Při výpočtu tuhosti se vycházelo z normových charakteristických hodnot hustoty dřeva, která byla dále upravena s ohledem na modelovaný spoj na hodnotu 390 kgm−3. Tyto hodnoty jsou charakteristické a dále se snižují podle vlivu délky trvání zatížení a typu prostředí, ve kterém bude spoj umístěn. Návrhové hodnoty by byly pro krátkodobé zatížení a 3. třídu prostředí cca Rd = 25 kN a Kd = 7,40 MNm−1 pro dva střihy na jeden svorník. Pro hustotu dřeva vzorku ρ520 = 520 kgm−3 je charakteristická normová tuhost v prokluzu pro dva střihy K520 = 23,702 MNm−1. Reálné spoje mají prvotní tuhost po aktivaci mechanického spojovacího prostředku ve dřevě 2–2,5krát vyšší v prokluzu než normou daná hodnota. Proto je nutné k tomuto faktu přihlédnout při porovnávání numericky získaných hodnot s testovanými daty vyrobených spojů. Schéma prokluzu spoje pro celou kulatinu je na Obr. 4.
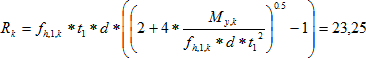 (3)
[kN]
(3)
[kN]
kde je
- F
- síla závislá na tuhosti spoje [N]
- Kser
- tuhost jednostřižného spoje [Nmm−1]
- ∆
- posun spoje v místě napojení [m]
- ρ
- hustota dřeva 390 kgm−3 [kgm−3]
- d
- průměr spojovacího prostředku [m]
- Rk
- charakteristická únosnost jednostřižného spoje [kN]
- fh,1,k
- charakteristická pevnost v otlačení dřeva [Nmm−2]
- t1
- délka otlačení na jeden střih svorníku [m]
- My,k
- plastický moment únosnosti spojovacího prostředku [Nmm]
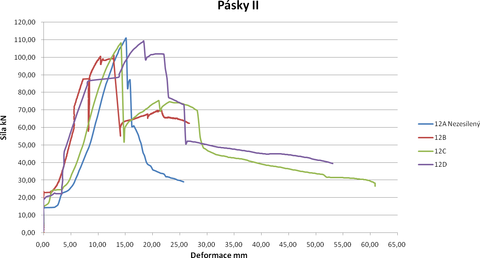
Obr. 5: Kulatina 9 vlhkost: 12 %, hustota cca 530 kg/m3 test, (značení A–D označuje jednotlivé laboratorní zkoušky daného typu spoje)
Na Obr. 5 je grafické znázornění z testování spoje dřevěné kulatiny na tah. Celkově se zkoušely čtyři vzorky. Zkoušky byly provedeny na Fakultě stavební VŠB-TU Ostrava. Obr. 6 a 7 zachycují připravené vzorky na laboratorní zkoušky. Podle průběhu jednotlivých křivek z testovacího zařízení je vidět znatelný prokluz, než dojde k aktivaci svorníku a tím ke zvýšení tuhosti spoje.
Grafy končí křehkým porušení ve dřevě. Je to způsobeno povahou dřeva jako přírodního materiálu a také skutečností, že dřevo na tah rovnoběžně a kolmo na vlákna má při vyčerpání únosnosti povahu křehkého porušení. Také ve smyku se dřevo chová při porušení křehce. Ocelový pásek podle provedených zkoušek není schopen zvýšit únosnost spoje, ale je schopen, než dojde k fatálnímu porušení vzorku, ještě určitou dobu udržet zatížení, které je na mezi porušení nevyztužené kulatiny.
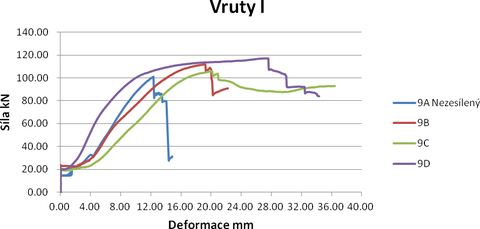
Obr. 8: Kulatina 9 vlhkost: 12 %, hustota 520 kg/m3 test, (značení A–D označuje jednotlivé laboratorní zkoušky daného typu spoje)
Na Obr. 8 jsou zobrazeny výsledky laboratorních zkoušek spoje kulatiny. Celkově se zkoušely čtyři vzorky. Na základě provedených laboratorních zkoušek byl proveden výpočet numerických modelů s různým materiálovým nastavením. Ortotropní model dřeva přepokládal bilineární pracovní diagramy. Ocel ve spojích měla také bilineární pracovní diagram.
Na Obr. 9 až 12 jsou grafické výstupy z numerického modelu TSK 1. Jedná se o model nevyztuženého spoje. Tento model měl za úkol naladit vlastnosti materiálu do dalších numerických modelů TSK 2 a TSK 3. Jak je vidět na Obr. 8, vruty jsou schopny zvýšit únosnost spoje a také zvýšit jeho duktilní chování.
Na Obr. 13 až 16 jsou grafické výstupy z numerického modelu TSK 2. Jde o model spoje vyztuženého vruty kolmo na vlákna. Zde bylo dosaženo nejlepšího výsledného vyztužení. Tento způsob vyztužení je nejvhodnější a to z důvodu jeho účinnosti a proveditelnosti. Vruty přímo sepnou dřevo a přechází do nich část tahu kolmo na vlákna. Vruty jsou duktilní a mohou přenášet velké tahové síly a částečně také ohybové účinky. Vruty je snadné instalovat a jsou chráněny před klimatickými změnami a neoslabují průřez (pokud nejsou předvrtané a jejich průměr není větší jak 6 mm). Toto vyztužení je požárně odolné a není v pohledové části, takže nemá rušivý charakter. Sepnutí vruty je jedno z účinných standardních vyztužení pro tah kolmo na vlákna.
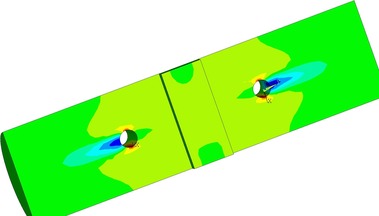
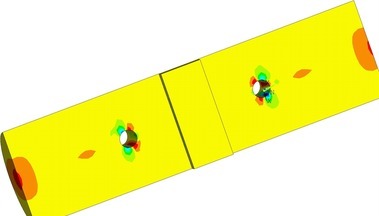
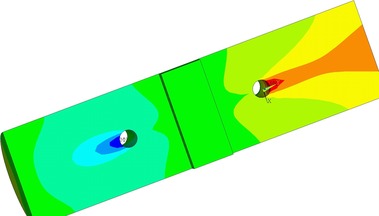
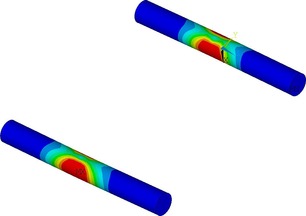
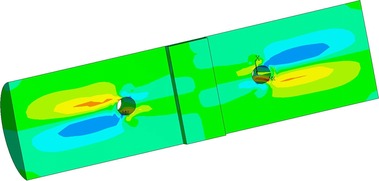
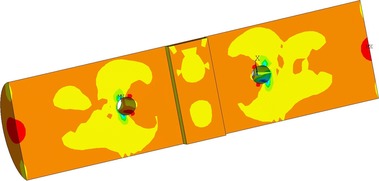
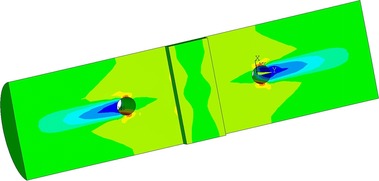
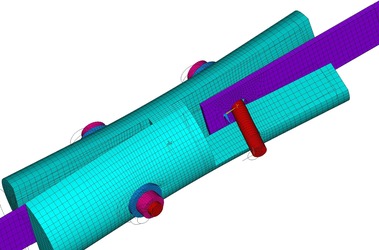
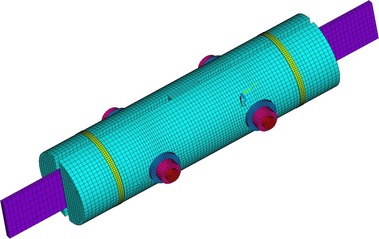
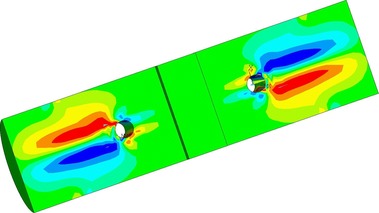
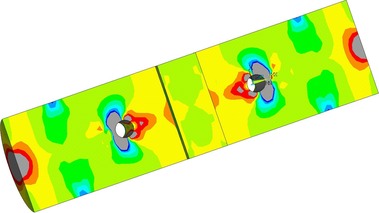
Na Obr. 17 a 18 je vidět konečně prvková síť numerických modelů. Na obrázku 19 je napětí ve smyku po objemu dřeva. Napětí kolmo na vlákna je zobrazeno na Obr. 20. Na modelu TSK 3 nebylo znatelné zlepšení únosnosti vlivem bandáže ocelovým páskem. Vzhledem k povaze porušení dřeva rozštípnutím vlivem tahu kolmo na vlákna není toto ztužení výhodné. Porušení se děje po objemu dřeva a pásek není schopen napětí kolmo na vlákna zachytit a účinně vyztužit spoj. Aby pásky byly účinné, je nutné je ještě aktivovat do tahu a to není pro běžné použití možné. Důvodem je samotné vymizení předpětí vlivem popuštění v kotvení, dále změna teplot a významné změny v objemu dřeva vlivem vlhkosti. Proto tento způsob vyztužení spoje není dostatečně účinný.
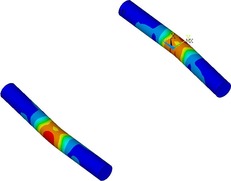
Na sledu Obr. 21 je vidět porušení rozštípáním pro test s ocelovými pásky TSK 3. Dále jsou zde numerické modely se sítí konečných prvků a vnitřní pohled na deformované vruty + celková globální deformace celého spoje.
Obr. 21: Testovaný vyztužený vzorek s páskem a numerický model s vrutem
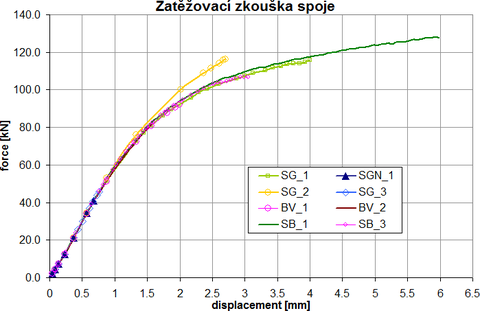
Obr. 22: Numericky testované modely kulatiny ANSYS (označení SG, BV, SB, SGN je pro doporučované parametry anizotropního zpevnění zvoleného materiálového modelu)
Numerické modely byly počítány geometricky a fyzikálně nelineárně s uvážením ortotropních vlastností dřeva a kontaktní povahy spojů. Numericky výsledky pro testované modely kulatiny jsou na obr. 22. Výpočet je proveden ve variantním označení SG, BV, SB a SGN pro doporučované parametry anizotropního zpevnění zvoleného materiálového modelu. Podle dosažených výsledků na numerických modelech byla konstatována dobrá shoda s laboratorními zkouškami. Maximální dosažená únosnost v numerickém modelu nevyztuženého spoje TSK 1 byla 82 kN a pro vyztužený numerický model vruty TSK 2 a numerický model s ocelovým páskem TSK 3 přibližně 112 kN. Tyto numericky dosažené hodnoty korespondují s reálnými testy spojů kulatiny.
Numerický model se chová stabilně do dosažení předepsané deformace cca 4,0 mm. Při vyšších deformacích plastizuje ocelový svorník a dochází k otlačení vývrtu pro svorník a rozštípání dřeva vlivem tahu kolmo na vlákna.
Numerické modely je třeba dále verifikovat laboratorními zkouškami jak spojů, tak i materiálů.
Závěr
Po analýze experimentálně a numericky získaných výsledků se dá konstatovat, že matematické modely se shodují s experimentálně získanými daty v maximu dosažené únosnosti pro jednotlivé druhy zesílení. V počáteční tuhosti je shoda také dobrá, ale je třeba vzít v úvahu různý prokluz u zkušebních modelů spojů. Tento prokluz nebyl u numerických modelů uvažován z důvodu jeho různorodosti a velkého rozptylu materiálových vlastností a výrobních tolerancí pro jednotlivé kusy spojů dřevěné části kulatiny.
Porovnání bylo prováděno jen u staticky zatížených spojů. Celková deformace u zkušebních testů je vyšší než u numericky získaných dat. Je to především kvůli zmíněným prokluzům, které zde mohou být výrazného charakteru z důvodu provádění vývrtů, a také proto, že jde o rostlé dřevo.
Na závěr lze konstatovat, že výsledky z numerického modelování se blíží k hodnotám získaných z laboratorních testů. Díky numerickým modelům je možná přesnější předběžná optimalizace zesílení a určení kritických oblastí kumulující vysoká napětí, především v tahu kolmo na vlákna a smyková napětí.
Poděkování
Práce byly podporovány z prostředků koncepčního rozvoje vědy, výzkumu a inovací pro rok 2014, přidělených VŠB-TU Ostrava Ministerstvem školství, mládeže a tělovýchovy České republiky.
Literatura
- [1] CECCOTTI, A. Timber–concrete composite structures. H. Blass (Ed.), Timber engineering-step 2, Centrum Hout, The Netherlands, 1995.
- [2] ČSN 73 1702 mod DIN 1052:2004 Navrhování, výpočet a posouzení dřevěných stavebních konstrukcí – Obecná pravidla a pravidla pro pozemní stavby. Praha: ČNI. 2007. 174 s.
- [3] ČSN EN 1995-1-1 73 1701 Eurokód 5: Navrhování dřevěných konstrukcí – Část 1-1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby. Praha: ČNI. 2006. 114 s.
- [4] GUAN, Z. W., ZHU, E.,C. Finite element modelling of anisotropic elasto-plastic timber composite beams with openings, Engineering Structure, 31, 2009, 394–403.
- [5] GUNDERSON, R. A., GOODMAN, J. R., BODIG, J. Plate Tests for Determination of Elastic Parameters of Wood, Wood Science, Vol. 5., p. 241–248, April 1973.
- [6] JOHNSSON, H. Plug Shear Failure in Nailed Timber Connections – Avoiding Brittle and Promoting Ductile Failures. Doctoral thesis, Div. of Timber Structures, Luleå University of Technology, 2004:03.
- [7] KOŽELOUH, B. Navrhování, výpočet a posuzování dřevěných stavebních konstrukcí, Obecná pravidla pro pozemní stavby, Komentář k ČSN 73 1702:2007, Praha: ČKAIT, 228 s, 2008, ISBN 978-80-87093-73-3.
- [8] KOŽELOUH, B. Dřevěné konstrukce podle EUROKÓDU 5, STEP 2, Navrhování detailů a nosných systémů. Zlín: KODR, 2004, ISBN 80-86 769-13-5.
- [9] KOMATSU, K., HARADA, M, YAMANAKA, Y., INOUE, T. Development od glulam moment-resisting joints for mluti-storey timber buildings., In PTEC 94,11 15. 7. 1994, 1994.
- [10] KUKLÍK, P., KUKLÍKOVÁ, A. Methods for evaluation of structural timber. Dřevařsky Vyskum/Wood Research, Vol. 46, 2001, Iss. 1, pp. 1–10, ISSN 0012-6136.
- [11] LOKAJ, A. Timber Beam Reliability Assessment. In Konference Euro-SIBRAM 2002 Collloquium. Praha: ITAM CAS, 2002, s. 1–8.
- [12] LOKAJ, A. , KLAJMONOVÁ, K. Round timber bolted joints exposed to static and dynamic loading. Wood Research. Vol. 59, Iss. 3, 2014, Pages 439–448.
- [13] RELEASE 11 DOCUMENTATION FOR ANSYS, SAS IP, INC., 2007.
- [14] Scia Engineer [online]. 2012 [cit. 2012-01-01]. Dostupný z WWW: http://www.scia-online.com.
- [15] STRAKA, B. Navrhování dřevěných konstrukcí. Akademické nakladatelství. Brno: CERM, s.r.o., EXPERT Ostrava, 1996. ISBN 80-7204-015-4.
Dřevěná kulatina se v současnosti stále více používá na různé dřevěné konstrukce. Hodnoty pevnosti a tuhosti samotné kulatiny se běžně předpokládají rovné hodnotám pro deskové a hraněné řezivo. Článek, který se zabývá analýzou taženého ocelového spoje dřevěné kulatiny, je tudíž aktuální a prospěšný. Doporučuji k vydání na tzb info bez dalších úprav.
The paper analyses a drawn steel joint in round logs for which several types of reinforcements have been proposed. The load-carrying capacity of the reinforcements has been tested in laboratories. At the same time, numerical modelling has been performed - it has focused, in particular, on rigidity of the joints during the loading process. Physical and geometrical nonlinearities have been taken into account. The Finite Element Method and 3D computation models have been used in the numerical calculations.