Modelování podzemních stěn pomocí časově závislého elasto-plastického materiálového modelu
V tomto příspěvku bude představeno použití pokročilého časově závislého elasto-plastického materiálového modelu pro modelování podzemních stěn. Prostor je věnován tzv. Shotcrete modelu, který dokáže vystihnout vliv času. Součástí příspěvku je krátké shrnutí teoretických poznatků o časově závislém chování betonu a přístup normy ČSN EN 1992-1-1. Dále je popsán materiálový model Shotcrete a je provedena kalibrace materiálového modelu v dlouhodobém časovém horizontu na základě dat z laboratorních zkoušek. Následně je řešena reálná okrajová úloha hlubokého zářezu zajištěného železobetonovými podzemními stěnami s rozpěrami. Úloha je řešena v několika variantách, výsledky jednotlivých přístupů k řešení jsou porovnány a na závěr jsou diskutovány dosažené hodnoty vnitřních sil a deformací.
1. Úvod
Tento příspěvek se zabývá vlivem časově závislých jevů na chování podzemních stěn. Ve stěnách dochází k vlivům jako je pozvolný nárůst pružnostních a pevnostních charakteristik, dále pak dotvarování a smršťování, které trvají po celou dobu životnosti konstrukce. V běžné praxi jsou tyto vlivy buď zcela zanedbány a podzemní stěny jsou modelovány pomocí lineárně elastického prvku, případně je vliv dotvarování v dlouhodobých podmínkách zjednodušeně vystižen pomocí kombinace dvou prvků (deskostěnového a objemového).
Ani jedna z výše popsaných metod však neposkytuje komplexní přístup ke změnám, ke kterým v průběhu životnosti konstrukce dochází. V tomto příspěvku je představeno použití pokročilého materiálového modelu tzv. Shotcrete modelu [9], pomocí kterého lze vystihnout časově závislé chování betonu a nabízí možnost analýzy konstrukce v libovolném čase.
2. Časově závislé chování betonu
Návrhem betonových konstrukcí se zabývá norma [4], kde jsou jednotlivé druhy betonu klasifikovány podle pevnostních tříd v tlaku. Tyto tlakové pevnosti jsou udány pro čas 28 dní a více, stejně jako odpovídající Youngův modul pružnosti a pevnost v tahu. V průběhu zrání betonu však dochází k průběžnému nárůstu některých materiálových charakteristik.
Norma [4] počítá s nárůstem pružnostních a pevnostních charakteristik betonu v čase od vybudování konstrukce až po čas 28 dní, kdy se uvažuje dosažení plných hodnot pružnostních a pevnostních charakteristik. Pro vyčíslení vlastností v libovolném čase norma [4] uvažuje vliv druhu použitého cementu na průběh zrání (třída cementu R, N, S). Cement třídy R zajišťuje rychlý nárůst charakteristik v počátku zrání, cement třídy N pozvolnější a cement třídy S zajišťuje velmi pozvolný nárůst pružnostních a pevnostních charakteristik. Pro beton třídy C20/25 jsou křivky nárůstu pružnostních a pevnostních charakteristik zobrazeny v obrázcích. Zatímco pevnost v tlaku (Obr. 1 vlevo) a modul pružnosti (Obr. 1 vpravo) dosáhnou své maximální hodnoty v čase 28 dní, hodnota tahové pevnosti se pozvolna vyvíjí i po této lhůtě (Obr. 1 uprostřed).
Dotvarování, na rozdíl od druhého souvisejícího jevu smršťování, je závislé na zatížení (ilustrace jevu viz Obr. 2 vlevo), konkrétně na jeho velikosti, době trvání a době zrání betonu v momentě zatížení. Dle normy [4] je velikost poměrného přetvoření vyvolaného dotvarováním betonu εcc![]() přímo závislá na součiniteli dotvarování φ(∞, t0), konkrétní hodnota použitelná pro daný případ se dle postupu v normě spočítá v závislosti na okolní vlhkosti, rozměrech prvku a složení betonu. Je nutné upozornit na skutečnost, že norma uvažuje pouze dotvarování při tlakovém namáhání, případy creepového chování tažených vláken norma neumí vystihnout, což může způsobit problémy například u ohýbaných prvků, kde jsou na jedné straně vlákna tlačená a na druhé naopak tažená. Další omezení má norma [4] v případě změny zatížení v průběhu životnosti konstrukce, protože lze spočítat pouze uvažovanou velikost dotvarování ze znalosti aktuální napjatosti v čase. Tento přístup tedy nezahrnuje skutečnost, že nám historie změny napětí, zejména pak zatížení a následné odtížení, způsobuje nevratné změny a výrazně ovlivňuje aktuální stav deformace.
přímo závislá na součiniteli dotvarování φ(∞, t0), konkrétní hodnota použitelná pro daný případ se dle postupu v normě spočítá v závislosti na okolní vlhkosti, rozměrech prvku a složení betonu. Je nutné upozornit na skutečnost, že norma uvažuje pouze dotvarování při tlakovém namáhání, případy creepového chování tažených vláken norma neumí vystihnout, což může způsobit problémy například u ohýbaných prvků, kde jsou na jedné straně vlákna tlačená a na druhé naopak tažená. Další omezení má norma [4] v případě změny zatížení v průběhu životnosti konstrukce, protože lze spočítat pouze uvažovanou velikost dotvarování ze znalosti aktuální napjatosti v čase. Tento přístup tedy nezahrnuje skutečnost, že nám historie změny napětí, zejména pak zatížení a následné odtížení, způsobuje nevratné změny a výrazně ovlivňuje aktuální stav deformace.
![Obr. 2: Ilustrace působení časově závislých jevů v betonu – vlevo creep, vpravo smršťování (upraveno dle [5])](/docu/clanky/0270/027003o9.png)
Obr. 2: Ilustrace působení časově závislých jevů v betonu – vlevo creep, vpravo smršťování (upraveno dle [5])
Ke smršťování dochází nezávisle na hodnotě zatížení po celou dobu životnosti konstrukce, průběh smršťování je závislý na vlhkosti okolního prostředí a také na složení betonu (ilustrace jevu viz Obr. 2 vpravo). Dle normy [4] se dělí smršťování na dvě části, poměrné smršťování vysycháním (probíhá pomalu po celou dobu životnosti konstrukce) a poměrné autogenní smršťování (lineární funkce pevnosti betonu, hlavní část vzniká v počátečních dnech tvrdnutí betonu). Norma stanovuje postup, jak spočítat konečné poměrné smršťování. Základními proměnnými tohoto výpočtu jsou relativní vlhkost, pevnostní třída betonu a tloušťka konstrukce.
3. Pokročilý materiálový model – SHOTCRETE MATERIAL MODEL
Pokročilý materiálový model pro beton použitý v tomto příspěvku pro matematické modelování se nazývá Shotcrete model (SH model) [9]. Tento materiálový model je definován jako elasto-plastický a původně byl vytvořen pro stříkaný beton, používaný jako primární ostění tunelů budovaných NATM, lze jej však použít ve všech aplikacích, kde potřebujeme zahrnout vliv časově závislého chování betonu. Tento model zahrnuje zpevňování a změkčování, časově závislé chování – nárůst pevnostních a pružnostních parametrů a také creep a smršťování. Celkové poměrné deformace jsou následně sumou čtyř složek: elastické, plastické, creepové a od smršťování, dle vzorce (4).
Plastické deformace jsou při použití SH modelu počítány dle definice elastoplasticity, v tlakové oblasti je plocha plasticity formulována dle Mohr-Coulomba, v tahové oblasti podle [8]. Pro zpevňování a změkčování byla pro tento materiálový model převzata pravidla z [10].
![Obr. 3: Grafické znázornění pracovního diagramu v oboru plastických přetvoření (křivka zpevňování a změkčování) SH modelu – vlevo v tlaku, vpravo v tahu (zpracováno dle [10] a upraveno)](/docu/clanky/0270/027003o12.png)
Obr. 3: Grafické znázornění pracovního diagramu v oboru plastických přetvoření (křivka zpevňování a změkčování) SH modelu – vlevo v tlaku, vpravo v tahu (zpracováno dle [10] a upraveno)
Pracovní diagram v oboru plastických přetvoření pro namáhání tlakem je zobrazen na Obr. 3 vlevo. Na vodorovné ose je vynesena hodnota parametru zpevňování a změkčování ![]() (v tlaku), kde
(v tlaku), kde ![]() je plastické přetvoření při dosažení tlakové pevnosti a
je plastické přetvoření při dosažení tlakové pevnosti a ![]() je aktuální hodnota hlavního plastického přetvoření. Na svislé ose je nanesen poměr působícího hlavního napětí k pevnosti v prostém tlaku σ3 / fc. Diagram se skládá ze čtyř částí: I) oblast nelineárního zpevňování, II) oblast lineárního změkčování (plocha pod druhou větví pracovního diagramu = lomová energie v tlaku Gc ), III) oblast lineárního změkčování, IV) reziduální pevnost. Před dosažením fc0n je odezva lineárně elastická. Pracovní diagram v oboru plastických přetvoření pro namáhání tahem je zobrazen na Obr. 3 vpravo. Na vodorovné ose je zobrazena hodnota parametru zpevňování a změkčování
je aktuální hodnota hlavního plastického přetvoření. Na svislé ose je nanesen poměr působícího hlavního napětí k pevnosti v prostém tlaku σ3 / fc. Diagram se skládá ze čtyř částí: I) oblast nelineárního zpevňování, II) oblast lineárního změkčování (plocha pod druhou větví pracovního diagramu = lomová energie v tlaku Gc ), III) oblast lineárního změkčování, IV) reziduální pevnost. Před dosažením fc0n je odezva lineárně elastická. Pracovní diagram v oboru plastických přetvoření pro namáhání tahem je zobrazen na Obr. 3 vpravo. Na vodorovné ose je zobrazena hodnota parametru zpevňování a změkčování ![]() (v tahu), kde
(v tahu), kde ![]() je plastické přetvoření při dosažení reziduální tahové pevnosti, a
je plastické přetvoření při dosažení reziduální tahové pevnosti, a ![]() je aktuální hodnota hlavního plastického přetvoření. Na svislé ose je nanesen poměr působícího hlavního napětí k pevnosti v tahu σ1 / ft . Diagram se skládá ze dvou větví: I) lineární změkčování (plocha pod první větví pracovního diagramu = lomová energie v tahu Gt ), II) reziduální pevnost.
je aktuální hodnota hlavního plastického přetvoření. Na svislé ose je nanesen poměr působícího hlavního napětí k pevnosti v tahu σ1 / ft . Diagram se skládá ze dvou větví: I) lineární změkčování (plocha pod první větví pracovního diagramu = lomová energie v tahu Gt ), II) reziduální pevnost.
SH model má možnost vystihnout změny jednotlivých materiálových veličin v čase, proto je jeho použití ideální pro výpočty metodou konečných prvků, neboť lze ve výpočtu provést v každém časovém okamžiku výpočet nových parametrů a upravit výpočet.
V jakémkoliv časovém okamžiku t lze vypočítat aktuální hodnotu E (t) dle vzorce (2). Pro výpočet nárustu pevnosti v čase platí obdobný vztah jako pro výpočet Youngova modulu pružnosti. V čase t se vypočítá hodnota tlakové pevnosti fc (t) dle vzorce (3).
Časově závislým jevem je také plasticita, mladý beton vykazuje vysokou hodnotu plastické duktility, která se následně postupem času rapidně snižuje, materiálový model vyžaduje zadání hodnot v čase 1 h (![]() ), 8 h (
), 8 h (![]() ) a 24 h (
) a 24 h (![]() ).
).
Dotvarování je v SH modelu definováno pomocí viskoelastického prvku, velikost poměrného přetvoření od dotvarování v čase εcr (t) je přímo řízena parametrem φcr (součinitel dotvarování), rychlost nárůstu creepové deformace je řízena parametrem ![]() (čas dosažení 50 % creepové deformace). Ze vzorce (4) lze vypočítat velikost creepové deformace, veličiny φcr a
(čas dosažení 50 % creepové deformace). Ze vzorce (4) lze vypočítat velikost creepové deformace, veličiny φcr a ![]() jsou parametry creepové deformace, σ je napětí, D matice tuhosti, t je aktuální čas a t0 je počátek zatěžování.
jsou parametry creepové deformace, σ je napětí, D matice tuhosti, t je aktuální čas a t0 je počátek zatěžování.
Ke smršťování přistupuje materiálový model podobně jako ke creepové deformaci, aktuální hodnota poměrné deformace od smršťování εshr (t) se vypočte dle vzorce (5), vstupními údaji jsou dva parametry ![]() (konečná hodnota smršťování v čase nekonečno) a
(konečná hodnota smršťování v čase nekonečno) a ![]() (čas dosažení 50 % konečné hodnoty smršťování), t je aktuální čas.
(čas dosažení 50 % konečné hodnoty smršťování), t je aktuální čas.
4. Řešení reálné okrajové úlohy
V rámci tohoto příspěvku byla řešena reálná okrajová úloha hlubokého zářezu zajištěného trvalými podzemními stěnami. Cílem studie bylo porovnat různé přístupy pro zahrnutí vlivu dotvarování betonu podzemních stěn.
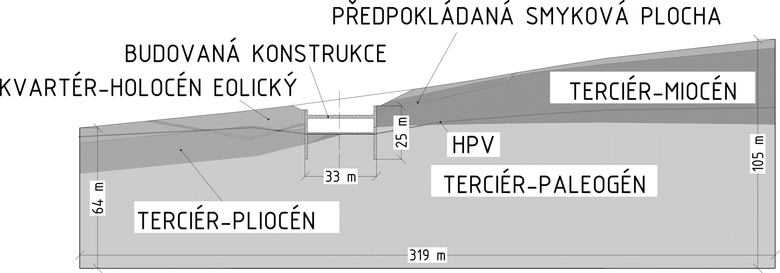
Inženýrsko-geologické podmínky řešené úlohy jsou významně ovlivněny předpokládaným výskytem svahových pohybů v místě budování zářezu (viz Obr. 4). Pod kvarterními pokryvnými útvary byly zastiženy zeminy charakteru převážně prachovitých jílů pliocenního stáří a jílů až prachovitých jílů miocenního stáří. Miocenní vrstvy jsou laminovány tenkými písčitými vrstvami. Pod sedimenty terciérního stáří se nachází vrstva paleogenních hornin (jílovce různého stupně zvětrávání). Smyková plocha je uvažována jako polygonální pás o tloušťce 1 m, ve kterém jsou uvažovány kritické smykové pevnosti. Pro zeminy byl použit materiálový model Hardening Soil se zvýšenou tuhostí v oboru malých přetvoření [1], pro skalní podloží Mohr-Coulombův model.
Řešenou okrajovou úlohou je hluboký silniční zářez, jehož definitivní zajištění je navrženo pomocí monolitických železobetonových podzemních stěn tloušťky 1200 mm v kombinaci s rozepřením ve dvou úrovních. Horní rozpěra společně s podélnými nosníky tvoří železobetonový rošt. Horní rozpěry mají rozměry 1200×1400 mm (šířka × výška) a jsou umístěny v osových vzdálenostech 6,6 m (tj. nejsou kontinuální). Spodní rozpěra je tvořená ŽB deskou tl. 750 mm a nachází se pod konstrukcí vozovky. Osová vzdálenost mezi podzemními stěnami je 31,8 m, podzemní stěny mají délku 22 m (levá) a 25 m (pravá). V průběhu výstavby jsou pro zajištění pravé podzemní stěny použity dočasné horninové kotvy ve dvou úrovních. Pro beton je jednotně uvažována třída C30/37, s objemovou hmotností 25 kN/m3.
| Parametr | E28 [kPa] | ν [–] | fc,28 [kPa] | fc0n [–] | fcfn [–] | fcun [–] | Gc,28 [kN/m] |
| Hodnota | 33.106 | 0,15 | 30.103 | 0,2 | 0,1 | 0,1 | 70 |
| Parametr | ϕmax [°] | ψ [°] | γfc [–] | ft,28 [kPa] | ftun [–] | Gt,28 [kN/m] | γft [–] |
| Hodnota | 40 | 5 | 1 | 3.103 | 1.10−3 | 0,148 | 1 |
| Parametr | thydr [den] | E1/E28 [–] | fc,1/fc,28 [–] | εcp,1hp [–] | εcp,8hp [–] | εcp,24hp [–] | a [–] |
| Hodnota | 28 | 0,65 | 0,3 | −0,03 | −1.10−3 | −0,7.10−3 | 20 |
| Parametr | ε∞shr [–] | t50shr [den] | ϕcr [–] | t50cr [den] | |||
| Hodnota | −2.10−5 | 86 | 0,8 | 40 | |||
Všechny vstupní parametry SH modelu použitého při řešení reálné okrajové úlohy jsou vypsány v tabulce (Tab. 1), parametry ovlivňující dotvarování a smršťování byly získány z kalibrace modelu na výsledcích laboratorních zkoušek (dle [7]). Pro kalibraci byla vybrána zkouška v prostém tlaku (válec) a zkouška v čtyřbodovém ohybu (kvádr), přičemž sledována byla poměrná deformace namáhaných vláken těles v čase při stanoveném zatěžovacím režimu. Zkoušky byly modelovány v programu Plaxis 2D za použití SH modelu, na tělesa bylo aplikováno zatížení vyvozující v extrémně namáhaných vláknech napětí odpovídající 50 % tlakové pevnosti (zkouška v prostém tlaku) a 50 % tahové pevnosti (zkouška v čtyřbodovém ohybu). Pro zjištění parametrů smršťování byla použita data o poměrném přetvoření nezatíženého tělesa. Kalibrací byly získány hodnoty 2 parametrů pro smršťování a 2 parametrů pro dotvarování, jejichž použití při simulaci zkoušky vedlo k nejlepší shodě se sadou dat získaných z laboratorních zkoušek [7]. Přesný průběh kalibračních zkoušek, výsledné kalibrační křivky a vstupní parametry zemin jsou podrobně popsány v diplomové práci [11].
Velikost matematického modelu 319 × 105 m byla volena tak, aby byly okrajové podmínky modelu v dostatečných vzdálenostech od budované konstrukce a další zvětšování modelu již nevedlo k významné změně výsledků. S ohledem na použití časově závislého materiálového modelu je důležité zohlednit časový průběh výstavby a následnou životnost konstrukce. Základní předpoklad pro výstavbu této konstrukce je zrání betonu 28 dní před počátkem jeho zatěžování (platí jak pro podzemní stěny, tak i rozpěry). Celková doba budování konstrukce je proto v tomto případě 150 dnů.
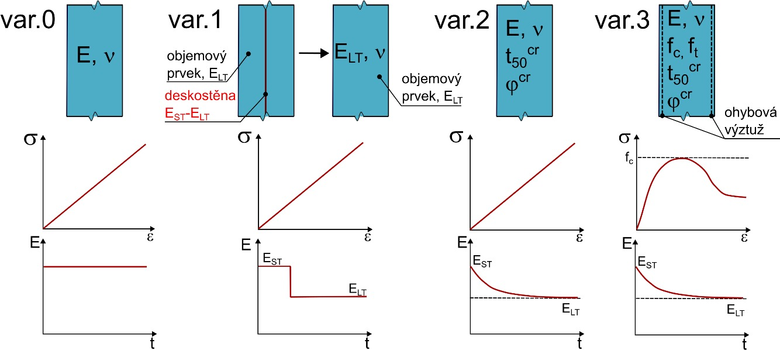
Reálná okrajová úloha byla řešena čtyřmi variantami výpočtu, jednotlivé varianty se liší použitým materiálovým modelem pro betonové konstrukce, inženýrsko-geologické podmínky jsou ve všech variantách totožné. Schéma variant výpočtu je znázorněno na Obr. 5.
Standardním řešením této úlohy je modelování podzemních stěn pomocí lineárně elastického materiálového modelu se zanedbáním vlivu dotvarování (var. 0).
První variantou se zohledněním vlivu dotvarování (var. 1) je modelování podzemních stěn pomocí kombinace objemového a deskostěnového prvku. Objemové prvky představují chování v dlouhodobém horizontu (ELT), v krátkodobých fázích jsou doplněny deskostěnovým prvkem (EST − ELT), který představuje rozdíl mezi dlouhodobou a krátkodobou tuhostí. Tato varianta předpokládá pouze existenci dvou stavů, není možné postihnout postupné změny.
Druhá varianta (var. 2) již zahrnuje plný časově závislý přístup, pro obě podzemní stěny i rozpěry je aplikován SH model. Pro vystižení betonových částí konstrukce je použit objemový prvek, faktor zanedbání vlivu výztuže je kompenzován pomocí uměle zvýšené tahové pevnosti.
Třetí varianta (var. 3) sestává z použití plného SH modelu pro betonové prvky, se skutečnou tahovou pevností, vliv výztuže je modelován pomocí dvou deskostěnových prvků při horním a spodním povrchu. V této variantě dostáváme nejvěrnější přístup k chování samotného betonu, odečítání vnitřních sil probíhá na objemovém prvku a je také nutné započítat příspěvek normálových sil v deskostěnovém prvku na rameni ke střednici stěny.
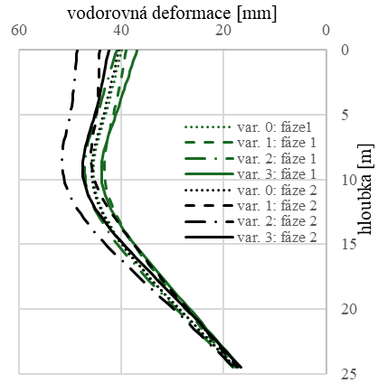
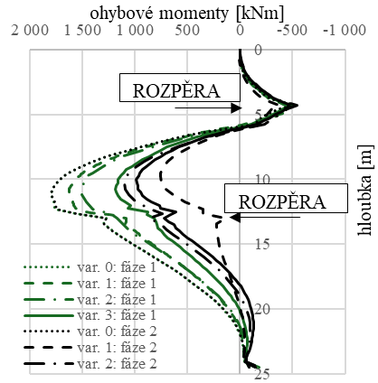
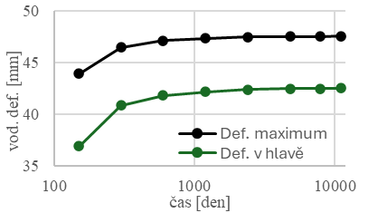
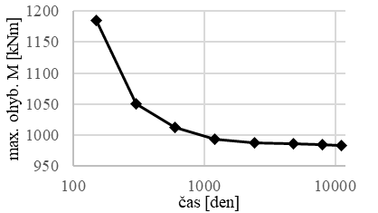
V této kapitole jsou znázorněny výsledky matematického modelování řešené reálné okrajové úlohy. Hlavními sledovanými parametry byla velikost ohybového momentu (Obr. 6 vpravo) a také vodorovné deformace pravé stěny (Obr. 6 vlevo). Ve výsledných grafech je respektováno předchozí označení výpočetních variant, naznačena je výšková úroveň rozpěr. V každé výpočetní variantě byly vzájemně porovnány výsledky ve sledovaných fázích: fáze 1 = Ukončení výstavby, fáze 2 = Životnost konstrukce/Provoz (30 let).
Přestože mají křivky momentů v jednotlivých fázích při porovnání variant výpočtu podobný průběh, maximální dosažené hodnoty se liší, zejména v pozdějších fázích výpočtu (dlouhodobé podmínky), nejmenší odchylky jsou zaznamenány v krátkodobých podmínkách.
V průběhu času dochází v konstrukci vlivem dotvarování a smršťování k tvarovým změnám, zvětšuje se vodorovná deformace konstrukce. Zároveň vlivem redistribuce vnitřních sil dochází ke snižování hodnot ohybových momentů. V případě varianty 0 není možné zahrnout vliv dotvarování, proto se křivky z fáze 1 i fáze 2 překrývají.
Z podrobné časové analýzy provedené pro variantu 3 (Obr. 7) vyplývá, že k tvarovým změnám dochází již v krátkodobých podmínkách a změnu vodorovných deformací v důsledku creepulze pozorovat již při budování konstrukce (hloubení stavební jámy), postupně se rychlost změny hodnot deformace a ohybového momentu snižuje. Varianty 2 a 3 díky použití SH modelu poskytují možnost analýzy těchto jevů i v krátkodobých podmínkách, stejně jako analýzu v kterémkoliv okamžiku životnosti konstrukce, lze tedy na základě měření na již vybudované konstrukci pravidelně vyhodnocovat deformace konstrukce a včas zajistit případné odchylky od předpokladů výpočtu.
5. Závěr
Cílem tohoto příspěvku byl rozbor možností, jak v matematickém modelu geotechnické konstrukce zahrnout vliv dotvarování betonu. Tato problematika je opodstatněná především u trvalých pažících konstrukcí. Dosažené výsledky byly porovnány s aktuálně používaným přístupem k této problematice. Nový přístup, založený na kombinaci pokročilého časově závislého elasto-plastického materiálového modelu pro beton a dvojice deskostěnových elastických prvků nahrazujících ohybovou výztuž, nabízí možnost analýzy konstrukce v kterémkoliv časovém okamžiku životnosti konstrukce. Jeho aplikace je však náročnější s ohledem na volbu vstupních parametrů do použitého materiálového modelu. V rámci této práce byla provedena kalibrace materiálového modelu na reálných laboratorních zkouškách a následně byl řešen matematický model zářezu zajištěného trvalými podzemními stěnami. Z výsledků matematického modelování vyplývá, že v průběhu životnosti konstrukce (zde uvažováno 30 let) dojde vlivem časově závislých jevů k poklesu ohybového momentu o 19,1 % a nárůstu vodorovné deformace o 8,3–15,2 %.
6. Literatura
- BENZ T. Small strain stiffness of soils and its numerical consequences. Stuttgart: Institut für Geotechnik, Universität Stuttgart, 2007. ISBN 978-3-921837-55-9.
- CEB-FIP model code. Design code – comite Euronational du Beton. London: Thomas Telford, 1990.
- ČSN EN 14487-1. Česká technická norma: Stříkaný beton – Část 1: Definice, specifikace a shoda. Praha: Český normalizační institut, 2006.
- ČSN EN 1992-1-1. Eurokód 2: Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. Praha: Český normalizační institut, 2006.
- MACGREGOR J. G. Reinforced Concrete : Mechanics and design. New Jersey: Prentice-Hall, Inc., 1997. Third Edition. ISBN 0-13-233974-9.
- PLAXIS Materials Model Manual 2019: Plaxis bv, Bentley Systems, Incorporated, 2019. ISBN-13: 978-90-76016-27-6.
- RANAIVOMANANA N. MULTON S. TURATSINZE A. Basic creep of concrete under compression, tension and bending. Construction and Building Materials, Elsevier 38, 173-180, 2013.
- RANKINE W. J. M. On the stability of loose earth. Philosophical Transactions of the Royal Society of London, Vol. 147, 1857.
- SCHÄDLICH B. SCHWEIGER H. F. A new constitutive model for shotcrete. Computational Geotechnics Group. Austria: Institute for Soil Mechanics and Foundation Engineering, Graz University of Technology, 2014.
- SCHÜTZ R. POTTS D.M. ZDRAVKOVIC L. Advanced constitutive modelling of shotcrete: Model formulation and calibration. Computers and Geotechnics, 2011, vol. 38, no. 6.
- ŠINDELÁŘOVÁ D. Modelování podzemních stěn pomocí časově závislého elasto-plastického materiálového modelu. Diplomová práce. Vysoké učení technické v Brně, Fakulta stavební, Ústav geotechniky. Vedoucí práce Ing. Juraj Chalmovský, Ph.D., 2022.
V předloženém příspěvku je výstižně analyzována problematika přístupu k výběru vhodného materiálového modelu při řešení okrajových úloh včetně komparace výsledků jednotlivých variant výpočtu. Akcentuji představení pokročilého materiálového modelu SHOTCRETE a zejména jeho aplikaci v rámci uvedené případové studie – reálné okrajové úlohy hlubokého zářezu, který je zajištěn trvalými podzemními stěnami. Za velice přínosné lze považovat výsledky variantního řešení, které jednoznačně potvrzují předpoklad nutnosti zahrnutí časově závislých jevů při řešení tohoto typu úloh, resp. přímo používání SH modelu v praxi.
Posuzovaný článek skvěle reaguje na problematiku volby materiálových modelů a přináší nový přístup pro řešení okrajových úloh se zahrnutím časově závislých jevů.
The main theme of this paper is the usage of the advanced time-dependent elasto-plastic material model for diaphragm walls modeling. First, a theory of time-dependent behaviour is briefly introduced. Next, the Shotcrete material model is described and calibration of materiál model in long term conditions based on laboratory testing is done. Finally, a real boundary value problem of deep excavation supported by diaphragm walls with the strut is solved. Reached values of intemal forces and deformations reached using different modelling methods are compared and discussed.

![Obr. 1a: Vývoj charakteristik betonu dle normy [4] – pevnost v tlaku](/docu/clanky/0270/027003o2.png)
![Obr. 1b: Vývoj charakteristik betonu dle normy [4] – pevnost v tahu](/docu/clanky/0270/027003o4.png)
![Obr. 1c: Vývoj charakteristik betonu dle normy [4] – modul pružnosti](/docu/clanky/0270/027003o6.png)