K možnostem nedestruktivního vyšetřování materiálových vlastností drátkobetonu
Používání drátkobetonu ve stavebních konstrukcích, podporované připravovanými technickými normami, stimuluje rozvoj metod pro nedestruktivní vyšetřování jeho struktury, podmiňující mechanické vlastnosti, např. odolnost vůči porušení při tahovém namáhání. Příspěvek ukazuje přehled dostupných metod, založených na zpracování obrazů a na měřeních elektromagnetických veličin.
1. Úvod
Drátkobeton, v mezinárodní terminologii obvykle FRC (z anglického názvu „Fibre-Reinforced Concrete“), tedy kompozitní materiál na cementové bázi vyztužený tenkými kovovými (nejčastěji ocelovými) drátky, se v poslední době ukazuje jako vhodný konstrukční materiál pro navrhování a realizaci nosných konstrukcí. Problematickou stránkou drátkobetonu je dosažení žádoucího prostorového rozložení drátků, zpravidla (z makroskopického pohledu) homogenního a izotropního, ve struktuře kompozitního materiálu. Dosažení takového rozložení, jež je ještě přijatelné pro konstrukční materiály, je podmíněno technologií výroby. Nezbytná jsou kontrolní měření nejen na čerstvých drátkobetonových směsích, ale i na ztvrdlých drátkobetonech, především na jejich exponovaných částech; výsledky těchto měření souvisejí se spolehlivostí i životností realizovaných konstrukcí.

 Obrázek 1: Kontrolní měření transparentních epoxidových vzorků s kovovými drátky v laboratoři na FAST VUT v Brně (nalevo) s detailním pohledem na používanou magnetickou sondu PeMaSo-2 (napravo)
Obrázek 1: Kontrolní měření transparentních epoxidových vzorků s kovovými drátky v laboratoři na FAST VUT v Brně (nalevo) s detailním pohledem na používanou magnetickou sondu PeMaSo-2 (napravo)Aktuální příprava technických norem [20], [21] a [22], vycházející ze zahraničních zkušeností (srov. [19]) zvyšuje zájem o spolehlivé a nepříliš nákladné nedestruktivní, případně aspoň málo invazivní zkoušení drátkobetonu v laboratorních podmínkách i na hotových stavebních konstrukcích. Klasický destruktivní přístup umožňuje jen pracně ověřit množství drátků ve vzorku, nikoliv již jejich orientaci, která může být klíčová pro výsledné mechanické vlastnosti, zejména pro prevenci porušení při tahovém namáhání. V tomto příspěvku se proto soustředíme na stručný přehled alternativních postupů, navržených a odzkoušených (včetně nezbytné výpočtové podpory) v posledních letech v rámci několika navazujících výzkumných projektů na Ústavu stavebního zkušebnictví FAST VUT v Brně (viz ilustrativní obr. 1), doplněný o odkazy na konkrétní aplikace i na hlubší fyzikální i matematické základy jednotlivých přístupů, ve snaze o otevření neformální diskuse na uvedené téma.
V dalších úvahách se soustředíme především na dva základní parametry materiálového vzorku:
- na objemový podíl drátků v materiálovém vzorku,
- na směrové rozložení drátků.
Jak uvidíme, optimální metoda pro levné a spolehlivé současné určení a) i b) za různých podmínek není dosud k dispozici, což lze interpretovat jako výzvu pro další základní i aplikovaný výzkum.
2. Metody založené na zpracování obrazů
Dostupnou skupinu přímých nedestruktivních metod představuje pořizování dvourozměrných či třírozměrných snímků testovaných vzorků a jejich následné vyhodnocování různými metodami zpracování obrazů (označovanými, často i v českých textech, souhrně jako „image processing“). Žádoucí jsou údaje o struktuře nejen o povrchu vzorku a blízké oblasti, ale o celém objemu vzorku. Příkladem dvourozměrného zpracování obrazů je tak opakované vyhodnocování promyšleně pořizovaných řad rentgenografických snímků, na rozdíl od výrazně nákladnějšího využití hardwarových i softwarových vymožeností počítačové tomografie (známé pod zkratkou CT, tj. „Computer Tomography“).
2.1 Zpracování dvourozměrných radiografických snímků
Využití radiografického snímkování představuje dnes již klasický nedestruktivní přístup k získávání informací o struktuře drátkobetonu, zejména typu b). Podrobněji se tomuto přístupu věnuje [6], kde se přímou detekcí polohy drátků z jednotlivých snímků zjišťuje jejich počet, příslušný jednotlivým třídám úhlů v rovině, z čehož lze následně sestavovat tzv. směrové růžice. Na grafických výstupech tohoto typu (jsou-li k dispozici v dostatečně reprezentativním množství) lze tak snadno kontrolovat, zda byla technologickým postupem dodržena makroskopická izotropie materiálu, důležitá pro zamezení vzniku trhlin při tahových namáháních z různých směrů. Problémy nicméně mohou být s idealizovanou makroskopickou homogenností materiálu, zejména při soustředění drátků (zejména při jejich poměrně nízkém objemovém podílu v materiálu), třeba i (přibližně) nahodilých směrů, do několika center, mezi nimiž zůstává nevyztužená matrice.
Věrohodné usuzování na prostorové rozložení drátků z jednoho snímku (či jejich malého množství), jakkoliv by bylo při známé délce drátků stejného typu teoreticky (klasickými metodami deskriptivní geometrie) možné, není realistické s ohledem na obvyklou kvalitu snímků a technologický postup při přípravě drátkobetonu. Detekce polohy drátků musí být dostatečně robustní, aby zpracovala i různě zakřivené drátky, případně i zmiňovaná nežádoucí centra.
Obecně je takové přímé zjišťování polohy drátků pracné, a tak se hledají alternativní, podstatně rychlejší přístupy – srov. [11]. Pro vyhodnocení rovinných snímků se nabízí rychlá diskrétní Fourierova transformace (algoritmus FFT, tj. „Fast Fourier Transform“). Uvažujeme-li (pro jednoduchost) úrovně šedé (bílé až černé) barvy f(x, y) na čtvercovém obrazu obsahujícím N × N pixelů (hypotetická limitní formulace s N → ∞ převádí součty na integrály, odpovídající klasické spojité transformaci), má diskrétní přímá a inverzní Fourierova transformace jednoduchý (i když stále komplexní) tvar
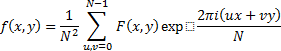
s tím, že veškeré informace potřebné k vytvoření směrové růžice obsahuje příslušné spektrum P(u, v) = |F(u, v)|2; podrobnosti (včetně instruktivních příkladů, pocházejících z konkrétních měření, srovnatelných s [6]) lze nalézt v [16] a [17].
2.2 Třírozměrná počítačová tomografie
Vyšší vývojový stupeň zpracování obrazů představuje průmyslová počítačová tomografie. Vhodná zařízení (jiná než zařízení pro lékařské aplikace, pracující na obdobném fyzikálním principu – podrobněji viz [18]) pro testování speciálních typů drátkobetonových vzorků (v předepsaném tvaru kvádru či válce) jsou na VUT k dispozici na výzkumných centrech CEITEC („Central European Institute of Technology“) a AdMaS („Advanced Materials, Structures and Technologies“). Jejich využití je nicméně výrazně omezeno nutností přípravy speciálních vzorků (a tedy praktickou nepoužitelností in situ) a značnými finančními náklady, jakož i nutností práce se specializovaným hardwarem a softwarem, jen obtížně přizpůsobovatelným vlastním potřebám. Pro konkrétní vzorek je nicméně tento přístup schopen poskytnout zcela přesné údaje a) i b) (v případě b) včetně prostorového zobecnění směrových růžic), což jej předurčuje jako vhodný ke kalibraci jiných, zejména nepřímých metod, konkrétně měření intenzity stacionárního magnetického pole Hallovou sondou podle obr. 1. Srovnání obou zmiňovaných přístupů je důkladně provedeno v [7] a [9].
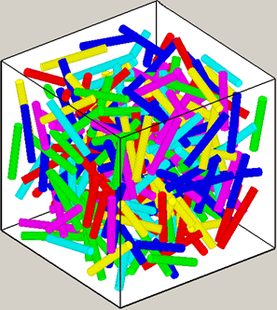
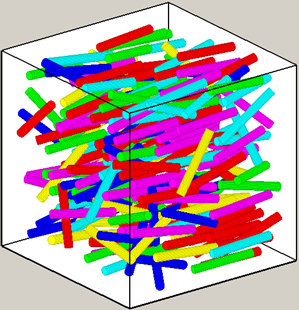 Obrázek 2: Generování vláknových struktur pro výpočtové modelování na základě teorie her – ukázka nahodilých směrů vláken (nalevo) a směrů vláken odpovídajících předem zadanému pravděpodobnostnímu rozdělení (napravo)
Obrázek 2: Generování vláknových struktur pro výpočtové modelování na základě teorie her – ukázka nahodilých směrů vláken (nalevo) a směrů vláken odpovídajících předem zadanému pravděpodobnostnímu rozdělení (napravo)Další možnosti využití přesných údajů o poloze drátků z tomografických snímků jsou diskutovány v [15]. Dosud nepublikovaný algoritmus softwarového generování polohy drátků ve směrech odpovídajících zadanému pravděpodobnostnímu rozdělení, navazující na výsledky [13], představuje východisko pro výpočtové modelování a simulaci nepřímých měření, zejména elektromagnetických, metodou Monte Carlo, případně dalšími metodami teorie her, s využitím standardních technik metody konečných prvků a objemů. Obr. 2 dokládá použitelnost tohoto přístupu i pro extrémně vysoký (hypotetický) objemový podíl drátků ve vzorku.
3. Metody založené na elektromagnetických měřeních
Vzhledem k nedostatečné informaci o a) z rentgenografických snímků a nákladnosti a omezenosti tomografického snímkování je účelné hledat alternativní, pokud možno nedestruktivní metody pro identifikaci a) – a nejlépe současně i b). Tyto metody jsou vesměs nepřímé, tedy vycházející z analogie s jinými fyzikálními procesy. Elektromagnetické metody, vhodné především pro kovové drátky, jsou založeny na rozdílné (relativní) magnetické permeabilitě, resp. dielektrické permitivitě, případně i dalších materiálových charakteristikách drátků a matrice v kompozitním materiálu. Aktuálnost vývoje takových metod, jejich rozšíření v posledních letech a možnost jejich podrobnější klasifikace dokumentuje [4].
Jistou nevýhodu předtavuje nutnost výpočtové homogenizace materiálových charakteristik, vedoucí k jejich jistým efektivním hodnotám, porovnávaným s naměřenými údaji. Obvyklé matematické teorie homogenizace, prezentované v [2], jmenovitě tzv. dvouškálová homogenizace, pracují teoreticky s deterministickými, přesně periodickými materiálovými strukturami, přičemž rozměry mikrostrukturálních objektů mají být natolik zanedbatelné, že je lze limitně zkoumat jako blížící se k nule. Zeslabení některého z uvedených předpokladů, zejména odstranění periodicity či připuštění stochastického charakteru materiálové struktury, je sice možné, ale vede k mimořádně komplikované matematické teorii konvergence na tzv. homogenizačních strukturách, diskutované v [12], od níž je k praktickým výpočtovým algoritmům dosud velmi daleko. I pro dvouškálovou konvergenci je třeba pro určení efektivních materiálových charakteristik, např. efektivní permitivity při studiu rozložení stacionárního magnetického pole, většin numericky ou řešit pomocný problém v podobě parciální diferenciální rovnice s periodickými okrajovými podmínkami; analytické výrazy jsou k dispozici jedině pro extrémně jednoduché (zpravidla nerealistické) případy, např. pro (předem předpokládaný) stejný směr veškerých drátků. Alternativně se proto v praxi často vychází ze zjednodušených předpokladů, zejména z různých variant teorie směsí – srov. [5].
3.1 Analýza stacionárního magnetického pole
Fyzikálně, matematicky i technicky jednodušší je analýza stacionárního magnetického pole, jejíž možnou praktickou realizaci, fungující na základě Hallova jevu, ukazuje obr. 1: permanentní magnet generuje magnetické pole, jehoiž zeslabení, měřené v jistých (vhodně volených) vzdálenostech od magnetu, vypovídá zprostředkovaně o a), méně již (neprovádí-li se experiment opakovaně v různých směrech) o b). Při představě o možné homogenizaci problému jde na makroskopické úrovni (přibližně) o řešení Laplacovy rovnice pro intenzitu magnetického pole, kde příslušná magnetická permeabilita vystupuje jen v okrajové podmínce; porovnání [17] s realističtější výpočtovou konfigurací včetně zahrnutí Hallovy sondy nicméně neukazuje významnou systémovou chybu takové idealizace.
V rámci této idealizace lze pro dostatečně nízký objemový podíl drátků (výrazně menší než na obr. 2, prakticky v souladu s [9] do 1 %) použít explicitní vzorec přizpůsobený z [5]
s μs odkazujícícm na (relativní) permeabilitu drátků (výrobci drátků zpravidla negarantovanou), s μc odkazujícím na známou (relativní) permeabilitu matrice (prakticky v našem případě většinou jednotkovou), přičemž μ je pak efektivní (relativní) permeabilita směsi; potřebné pomocné proměnné
obsahují tvarové parametry ϑ a ζ, jež lze vyjádřit (po delším výpočtu s limitním přechodem) jako
pro (přibližně) válcové drátky zjednodušené (kvůli hladkosti hranice) na protáhlé rotační elipsoidy, přičemž a a b jsou délka hlavní osy a (stejná) délka obou vedlejších os. Dodatečný netriviální problém nicméně představuje identifikace μ jako funkce ξ pro neznámou hodnotu μs na základě měření intenzity magnetického pole a numerické metody nejmenších čtverců, vycházející z [14]; podrobnější analýza je obsažena v [16]. Souvislost s reálnou kalibrační křivkou, odvozenou pro předem známé objemové podíly drátků, je zřejmá z [9], kde je rovněž dokumentována aplikace diskutované metody na drátkobetonové segmenty ostění tunelu, podrobené destruktivním zkouškám v Kloknerově ústavu ČVUT v Praze.
Obecně je nepominutelnou nevýhodou uvedeného postupu jeho částečná destruktivnost: k získání věrohodných (nikoliv jen předběžně informativních) výsledků, zejména o rozložení drátků hlouběji pod povrchem masívní konstrukce, je třeba v praxi provádět řadu vývrtů do hotové konstrukce (srov. obr. 1). V rámci analýzy stacionárního magnetického pole není tato nevýhoda dobře odstranitelná, neboť mimo polohu magnetů a Hallova senzoru nejsou pro případnou lepší organizaci experimentu k dispozici žádné další volitelné parametry.
3.2 Analýza nestacionárního elektromagnetického pole
Svůdným návodem k překonání kritizovaných nedostatků analýzy stacionárního elektromagnetického pole se zdá být přechod k analýze nestacionárního elektromagnetického pole. Mimo intenzitu magnetického pole H zde můžeme pracovat i s intenzitou elektrického pole E a s potřebnými materiálovými charakteristikami: dielektrickou permitivitou ε, elektrickou vodivostí σ a magnetickou permeabilitou μ (obecně maticové, zde pro jednoduchost výkladu uvažované jako skalární). Kompletní fyzikální a matematická analýza nicméně vede k počátečním a okrajovým úlohám pro soustavu Maxwellových parciálních diferenciálních rovnic, která dosud (vzhledem ke své výrazné nelinearitě) skrývá i různá teoretická úskalí a jejíž i přímé numerické řešení, nemluvě již o identifikačních problémech. Za řady zjednodušujících předpokladů lze nicméně (dosti dlouhým odvozením, provedeným v [15]) dospět k výsledným rovnicím
Obrázek 3: Ukázka přípravy transparentních epoxidových vzorků s garantovaným objemovým podílem a směrovým rozložením drátků (a) a hotový vzorek (b) s následným využitím experimentálního zařízení pracujícího s harmonickým elektromagnetickým polem, vyvíjeného ve spolupráci s Ústavem mikroelektroniky FEKT VUT v Brně (c)
Mimo standardní Laplacův operátor ještě horní tečky v těchto rovnicích naznačují derivace podle časové proměnné, které pro obecně nestacionární problém nelze ostranit. Pro speciální harmonické buzení lze nicméně tuto soustavu převést (opět způsobem naznačeným v [15]) do tvaru jediné formálně stacionární rovnice v komplexním oboru s volným parametrem budicí frekvence a s vhodnými okrajovými podmínkami.
Na uvedené myšlence je založena plně nedestruktivní elektromagnetická metoda testování a) i b). Detailní technický popis metody je dosud předmětem projednávaného návrhu na patentovou ochranu. Obr. 3 dokumentuje pratickou přípravu zkušebních vzorků a organizaci měření, prozatím v laboratorních podmínkách.
4. Predikce mechanických vlastností
Ve své podstatě geometrické charakteristiky a) a b) jsou sice podstatné pro predikci mechanických vlastností drátkobetonu, nicméně jeho krátkodobé i dlouhodobé vlastnosti ovlivňuje i řada dalších faktorů, např. soudržnost mezi výztuží a matricí či absence již zmiňované lokální koncentrace drátků. Ve shodě s [3] je třeba považovat za nejpodstatnější studium možného kvazikřehkého lomu drátkobetonu s cílem jeho vyloučení či aspoň maximálního omezení vhodným umístěním drátků (nebo dokonce i jejich promyšlenou orientací, i když zde se naráží na reálné technologické možnosti). Zachytit je třeba i tahová napětí, která vznikají v raných stádiích vývoje betonu v důsledku objemových změn, vyvolaných vybranými chemickými reakcemi.
Studium případných postkritických stavů (ve smyslu inicializace a šíření trhlin) představuje samostatný výzkumný problém, výpočtově zvládnutelný pomocí kohezních prvků pro modelování předem odhadnutelných trhlin, případně i vhodným rozšířením běžné metody konečných prvků (X-FEM čili „eXtended Finite Element Method“ apod.). Závažný problém pak ovšem (se zvýrazňováním nelineárního charakteru úlohy a uplatňováním nevratných fyzikálních dějů) představuje návrh a identifikace potřebných efektivních materiálových charakteristik.
Vztah mezi a), b) a dalšími měřitelnými charakteristikami na jedné straně a chováním zatížené konstrukce na bázi drátkobetonu na druhé straně představuje dodnes nevyřešený problém. Jeho řádné studium (s ohledem na přítomnost řady fyzikálních i chemických procesů, jež nelze zohlednit v relativně jednoduchém matematickém modelu) musí být nutně založeno na součinnosti experimentálních prací v různých typech laboratoří s vývojem původních nástrojů pro výpočtové simulace.
5. Závěr
V tomto příspěvku jsme se pokusili poukázat na význam problému identifikace struktury drátkobetonu pro jeho použití ve stavebních konstrukcích a prezentovat některé dostupné experimentální metody a relevantní výpočtové nástroje, reálně používané na FAST VUT v Brně. Podrobnosti o jejich praktických aplikacích lze většinou nalézt v odkazované literatuře.
S postupujícím studiem otevřených problémů v souvislosti se zkoušením drátkobetonu a predikcí jeho mechanických vlastností neubývá; tyto problémy nelze vyřešit odkazem na připravované technické normy [20], [21] a [22]. Příspěvek lze tak chápat i jako výzvu k diskusi a výzkumné spolupráci v nejbližší budoucnosti.
Poděkování
Tento příspěvek vznikl jako součást projektu LO1408 AdMaS UP – Advanced Materials, Structures and Technologies, podporovaného MŠMT ČR v rámci Národního programu udržitelnosti I.
Literatura
- BOULMEZAOUD, T.Z.; EL RHABI, M.: On time-harmonic Maxwell’s equations in Lipschitz and multiply-connected domains of R3. In: Monografías del Seminario Matemático García de Galdeano 27 (2003), p. 127–134.
- CIORANESCU, D.; DONATO, P.: An Introduction to Homogenization. Oxford University, 1999.
- CUNHA, V.M.C.F.; BARROS, J.A.O.; SENA-CRUZ, J.M.: An integrated approach for modelling the tensile behaviour of steel fibre reinforced self-compacting concrete. In: Cement and Concrete Research 41 (2011), p. 64–76.
- FAIFER, M.; FERRARA, L.; OTTOBONNI, R.; TOSCANI, S.: Low frequency electrical and magnetic methods for non-destructive analysis of fiber dispersion in fiber reinforced cementitious composites: an overview. In: Sensors 13 (2013), p. 1300–1318.
- GIORDANO, S.: Effective medium theory for dielectric ellipsoids. In: Journal of Electrostatics 58 (2003), pp. 59–76.
- HOBST, L.; ANTON, O.; VODIČKA, J.; ŠČUČKA, J.: Homogeneity detection of fibre-concrete structures by using radiographic technique. In: Nondestructive Testing of Materials and Structures 2012 – Proceedings of International Conference in Istanbul, p. 323–328. RILEM Bookseries 6, Springer, Berlin, 2013.
- HOBST, L.; BÍLEK, P.; ANTON, O.; ZIKMUND, T.: Stanovení přesné polohy drátků v kalibračních vzorcích drátkobetonu počítačovou tomografií. In: Zkoušení a jakost ve stavebnictví 2013 – sborník příspěvků konference v Brně, p. 33–42. VUT v Brně, 2013.
- HOBST, L.; BÍLEK, P.; LÁNÍK, J.; VODIČKA, J.: Předběžné měření koncentrace drátků v drátkonetonových segmentech ostění tunelu. In: Zkoušení a jakost ve stavebnictví 2014 – sborník příspěvků konference v Brně, p. 93–101. VUT v Brně, 2014.
- HOBST, L.; BÍLEK, P.; ANTON, O.; ZIKMUND, T.: Sledování anomálního rozmístění drátků v kalibračních vzorcích drátkobetonu počítačovou tomografií (CT). In: Sanace betonových konstrukcí – sborník přednášek XXIV. mezinárodního sympózia v Brně, p. 27–33. SSBK (Sdružení pro sanaci betonových konstrukcí), 2014.
- HOBST, L.; KOMÁRKOVÁ, T.; VALA, J.: Electromagnetic approach to nondestructive testing of fibre concrete. In: International Journal of Materials 2 (2015), p. 35–39.
- KÄRKKÄINEN, S.; VEDEL JENSEN, E.B.: Estimation of fibre orientation from digital images. In: Image Analysis and Stereology 20 (2001), p. 199–202.
- NGUETSENG, G.; SVANSTEDT, N.: ϭ-convergence. In: Banach Journal of Mathematical Analysis 5 (2011), pp. 101–135.
- POSPÍŠIL, T. On statistical description of random structures. In: Engineering Mechanics 17 (2010), p. 383–392.
- VALA, J.: Computational approaches to some inverse problems from engineering practice. In: PANM (Programs and Algorithms of Numerical Mathematics) – Proceedings of 17th Seminar in Dolní Maxov (2014), p. 215–230. Matematický ústav AV ČR v Praze, 2015.
- VALA, J.: Structure identification of metal fibre reinforced composites. In: Algoritmy 2016 – Proceedings of 20th Conference on Scientific Computing in Podbanské (Slovakia), p. 244–253. STU Bratislava, 2016.
- VALA, J.; HOBST, L.; KOZÁK, V.: Detection of metal fibres in cementitious composites based on signal and image processing approaches. In: WSEAS Transactions on Applied and Theoretical Mechanics 10 (2015), p. 39–46.
- VALA, J.; HORÁK, M.: Nondestructive identification of engineering properties of metal fibre composites. In: 10th ICNAAM (International Conference of Numerical Analysis and Applied Mathematics) in Kos (Greece) – Proceedings, p. 2208–2211. AIP (American Institute of Physics) Conference Proceedings 1479, 2012.
- WEIDEMANN, G.; STADIE, R.; HILLEMEIER, B.: Computer tomography study of fibre reinforced autoclaved aerated concrete. In: Materials Testing 50 (2008), p. 278–285.
- BS EN 14721: Test method for metallic fibre concrete – Measuring the fibre content in fresh and hardened concrete. BSI, 2005, 2007.
- ČSN P 732350: Vláknobeton – Specifikace, vlastnosti, výroba a shoda. Předběžná česká technická norma. ÚNMZ, 2015.
- ČSN P 732351: Vláknobeton – Zkoušení čerstvého vláknobetonu. Předběžná česká technická norma. ÚNMZ, 2015.
- ČSN P 732352: Vláknobeton – Zkoušení ztvrdlého vláknobetonu. Předběžná česká technická norma. ÚNMZ, 2015.
Posuzovaný příspěvek se zabývá především identifikací prostorového rozložení kovové disperzní výztuže v betonu resp. v tzv. „drátkobetonu“. Vlákny vyztužené betony procházejí vývojem již od roku 1965, kdy hlavním motivem pro jejich vývoj byla náhrada azbestových vláken, která jsou, jak se ukázalo, zejména ve vyšších koncentracích karcinogenní. Postupně se vyvinuly různé materiálové báze vláknobetonu (polypropylénová vlákna, skleněná vlákna, ocelová „vlákna“ – drátky). Zkoušky fyzikálně mechanických vlastností v posledních 50 letech prokázaly v případě vlákny vyztuženého betonu významný nárůst tzv. „rázové houževnatosti“, resp. vrubové pevnosti, tedy schopnosti odolávat šíření trhlin, zároveň se však ukázalo, že zejména při vyšších dávkách vláken může docházet i k poklesu mechanických vlastností,pokud vlákna negativně ovlivňují zpracovatelnost betonové směsi.
Praktické využití vláknobetonu ve stavebnictví je však stále velmi omezené. Polypropylénová vlákna se sice přidávají zejména do správkových malt pro sanace železobetonu s cílem minimalizovat vznik trhlin od tzv. hydratačního, resp. chemického smrštění, nízký modul pružnosti polypropylénu však vylučuje jejich využití jako účinného statického vyztužení. K tomuto účelu jsou okrajově používána skleněná vlákna, zejména však pak drátky, u nichž dominantní oblasti použití v současném stavebnictví je zhotovování interiérových podlahových desek zejména průmyslových podlah. Jejich vliv na fyzikálně mechanické vlastnosti betonu souvisí jak s jejich dávkou, která má v posledních 20 letech stále klesající tendenci, tak s jejich homogenizací.
Právě posuzovaný příspěvek se zaměřuje dominantně na možnosti charakterizace rozmístění drátkové výztuže v betonu. Jeho význam spočívá především v popisu limitujících podmínek, které tuto přesnější charakterizaci omezují. V současnosti je reálně k dispozici buď možnost stanovení obsahu drátku v čerstvé betonové směsi jejím rozplavením nebo separace drátků ze zatvrdlého betonu po provedení destruktivních zkoušek. Je bohužel skutečností, že obsahy drátků zjišťované většinou v omezeném počtu jádrových vývrtů, odebraných z podlahových konstrukcí, jsou vždy významně pod minimální úrovní, předepsanou projektem (25 až 30 kg/m3). Je to nepochybně ovlivněno tím, že homogenizace drátků v autodomíchávači je problematická a odporuje běžným zásadám. Autodomíchávač není míchací zařízení a současně samospádové míchání je pro homogenizaci drátků nevhodné. Bylo by proto velkou zásluhou, kdyby kromě pokusů o identifikaci míry rozptylu drátků v betonu byl definován minimální počet vývrtů, resp. objem betonu, který by byl pro prokázání obsahu drátků v zatvrdlém betonu dostatečně průkazný. Vláknová výztuž může nepochybně efektivně plnit specifické úkoly zejména v dynamicky namáhaných konstrukcích. Neměla by se však stát pouze formální substitucí standardně vyztuženého betonu.
Utilization of fibre concrete in building structures, supported by technical standards in preparation, stimulates the development of methods for nondestructive analysis of its structure, crucial for mechanical properties, as fracture resistance under tensile loads. The paper presents an overview of available methods, based i) on image processing and ii) on measurements of electromagnetic quantities.


