Srovnání MC 2010 a ČSN 73 2452 při zatřídění drátkobetonu do pevnostní třídy
Využití drátkobetonu při návrhu nosných drátkobetonových konstrukcí předpokládá, že vyrobený drátkobeton bude zatříděn do pevnostních tříd. Pro statický návrh jsou nezbytné uvedené pevnosti v pevnostní třídě: tlak, tah při vzniku trhlin a dohodnutém přetvoření při ohybové zkoušce trámců. V příspěvku bude ukázán postup, při stanovení pevnostní třídy drátkobetonu podle uvedených předpisů. Různé uspořádání zkušebního zařízení, rozdíly v rozpětí zkušebních trámců a jejich úpravy ovlivní postup při vyhodnocení uvedených tahových pevností včetně výsledných pevnostních tříd. Pevnosti v tlaku posuzovaného drátkobetonu je v souladu s hodnocením obyčejného betonu (válce/krychle). Uvedené pevnostní třídy, stanovené dvěma metodikami, ukazují rozdíl zatřídění jednoho typu drátkobetonu, v tomto případě při zvyšování pevnosti drátkobetonu po vzniku makrotrhliny způsobených vyšší hmotnostní koncentrací drátků.
1 Úvod
Cílem příspěvku je porovnat dva možné postupy při zatřídění jednoho typu drátkobetonu do pevnostní třídy (MC 2010 a ČSN 73 2452) na základě výsledků uskutečněných průkazních zkoušek v souladu s uvedenými dokumenty.
S ohledem na rozsah příspěvku a poukázání na odlišnost obou postupů je porovnání provedeno pouze pro oblast pevností v tahu drátkobetonu s pracovními diagramy využitelnými při návrhu drátkobetonvých konstrukcí na únosnost (MSÚ).
Pro oba uvedené pracovní diagramy:
- MC 2010 – Rigid plastic Model,
- ČSN 73 2452 – zjednodušený pracovní diagram,
bylo využito předem provedeného zatřídění vyrobeného drátkobetonu do pevnostní třídy podle pevnosti v tlaku. Pro výpočet tahových pevností tak bylo využito stejné pevnostní třídy drátkobetonu v tlaku FRC 50/60, prokázané zkouškami na válcích (MC 2010) a krychlích (ČSN 73 2452).
2 Charakteristiky drátkobetonu v tahu
2.1 Model Code 2010 (MC 2010)
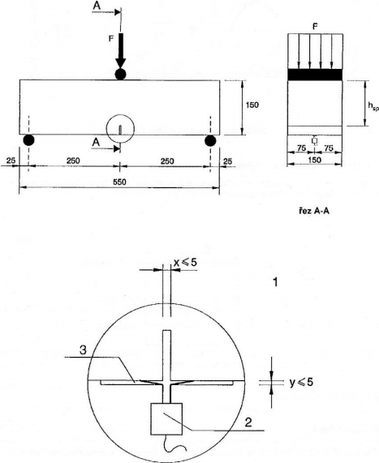
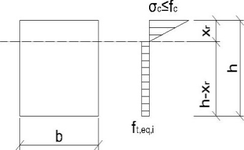
Vlastnosti ztvrdlého drátkobetonu v tahu se odvozují ze zkoušek trámců při tříbodovém uspořádání zkoušek ohybem na trámcích (Obr. 1) podle převzaté normy ČSN EN 14 651 + A1 (Obr. 2).
Obr. 1 Typické uspořádání při měření rozevření trhliny (CMOD)
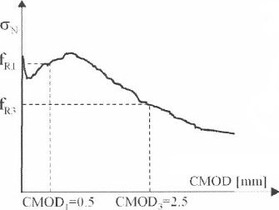
Obr. 2 Typické výsledky ohybové zkoušky
MC 2010 značí drátkobetony podle tzv. ekvivalentní (reziduální – zbytkové) pevnosti v tahu za ohybu jako napětí, které bylo zjištěno za předpokladu průřezu bez trhliny (lineární chování):
(1)
[MPa]
kde je
- fR,j
- [MPa] zbytková pevnost v tahu za ohybu odpovídající CMOD = CMODj nebo δ = δj,
- Fj
- [N] zatížení odpovídající CMOD = CMODj nebo δ = δj,
- l
- [mm] délka rozpětí,
- b
- [mm] šířka zkušebního tělesa,
- hsp
- [mm] vzdálenost mezi koncem zářezu a horní hranou zkušebního tělesa.
2.2 Vyčíslení tahových pevností podle MC 2010
Výchozím podkladem je diagram F–w (síla – šířka trhliny). Zaznamenané křivky charakterizující chování trámců namáhaných ohybem řízenou deformací reprezentují chování drátkobetonu ve zkoušených trámcích s možností odvození pevnosti v tahu za ohybu (ffc,Rj).
Pro zatřídění těchto pevností do pevnostní třídy je třeba stanovit výpočtem dvě křivky reprezentující jednotlivé zkušební záznamy, a to průměrné hodnoty (ffc,Rm) a charakteristické hodnoty (ffc,Rk) – viz Obr. 3.
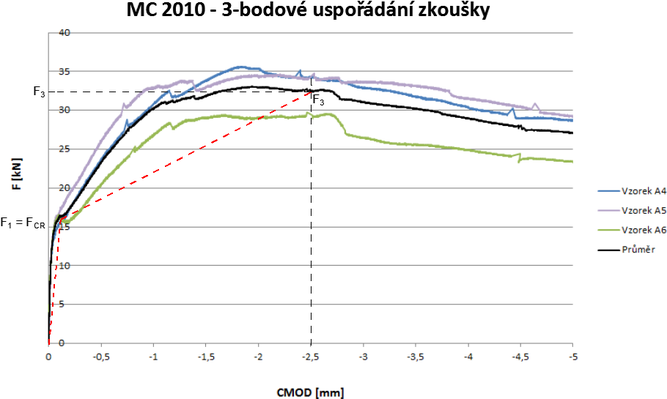
Obr. 3 Diagram F–w (síla – šířka trhliny) získaný ze zkoušky ohybem při 3bodovém uspořádání zatížení
Odvozené pevnosti v tahu za ohybu spolu s vytvořenými pracovními diagramy podle Obr. 3 platí pouze pro MSÚ.
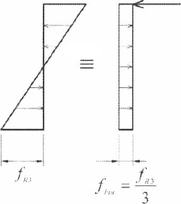
MC 2010 umožňuje pro návrh drátkobetonových konstrukcí podle MSÚ použít jeden ze dvou zjednodušených pracovních diagramů, které jsou založeny na velikosti šířky trhlin (CMOD 1-3). V případě tohoto posouzení je uveden pouze Rigid plastic model.
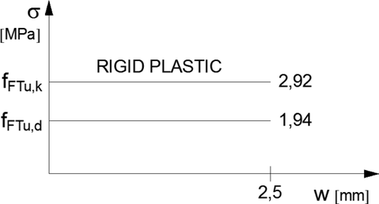
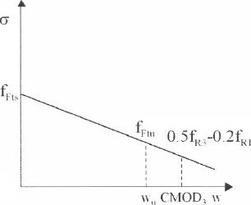
V případě přijetí tzv. pracovního diagramu „Rigid plastic“ se vychází z CMOD 3 (wu = 2,5 mm) a výpočtu napětí podle Obr. 4.
(2)
[MPa]
(3)
[MPa]
kde je
- γM
- – zvolený součinitel bezpečnosti.
Obr. 4 Zjednodušený model napětí přijatý pro výpočet maximální zbytkové pevnosti v tahu za ohybu
Obr. 5 Pracovní diagram „Rigid plastic“
2.3 TP FC 1-1 2007 (Technické podmínky pro zkoušení drátkobetonu a jejich hodnocení)
Vlastnosti ztvrdlého vláknobetonu v tahu se odvozují z tzv. diagramu odolnosti – závislosti síla – průhyb (F–δ). Ze zkoušek trámců ohybem řízenou deformací ∆δt (s = 0,2 mm/min) při čtyřbodovém uspořádání zatížení (Obr. 6) podle ČSN 73 2452 „Zkoušení ztvrdlého vláknobetonu“.
Uvedená norma je jednou ze tří norem:
- ČSN 73 2450 „Vlastnosti FRC – specifikace, vlastnosti, výroba a shoda“,
- ČSN 73 2451 „Zkoušení čerstvého vláknobetonu“,
- ČSN 73 2452 „Zkoušení ztvrdlého vláknobetonu“,
vypracovaných Katedrou betonových a zděných konstrukcí, FSv ČVUT v Praze a firmou Betotech za přispění členů 10.SK při NSK 36 – Betonové konstrukce.
Normy respektují základní pravidla zavedené evropské normy EC2 pro navrhování betonových konstrukcí, podle ČSN EN 1992-1-1.
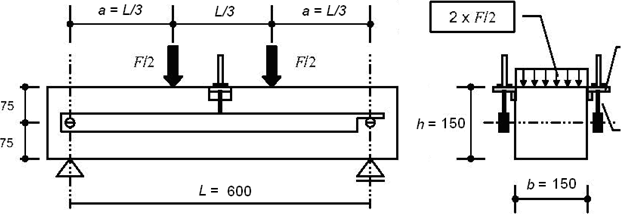
Obr. 6 Schéma uspořádání zkoušky ohybem při čtyřbodovém uspořádání zatížení
2.4 Vyčíslení tahových pevností podle ČSN 73 2452 (TP FC 1-1 2007))
Výchozím podkladem je tzv. diagram odolnosti (F–δ). Stejně jako v případě MC 2010 diagramu (F–w) musí být dílčí záznamy zkoušek zpracovány statisticky, tj. ze zaznamenaných křivek zkoušených trámců odvozeny křivky charakterizující průměrné a charakteristické hodnoty naměřených sil Fe,i,j připravených pro odečtení sil FEm a FEk ve zvolených průhybech trámců δti.
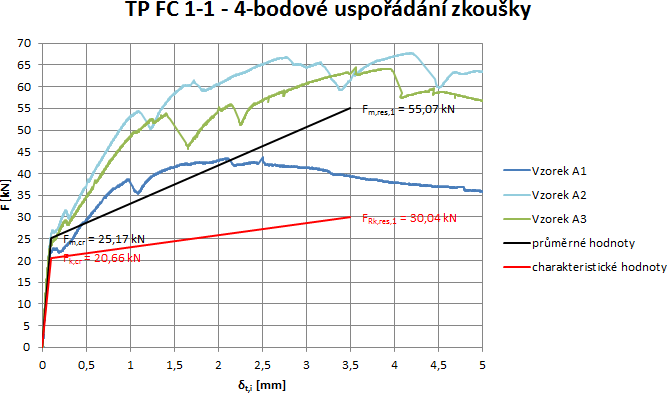
Obr. 7 Diagram odolnosti (síla – průhyb) získaný ze zkoušky ohybem při 4bodovém uspořádání zatížení
Odvození pevnosti drátkobetonu v tahu pro zjednodušený diagram využitelný při návrhu podle MSÚ je třeba vyčíslit pevnosti v tahu pro zvolené velikosti průhybu δi:
- δ0,15-0,3 ≈ odpovídá velikosti průhybu při vzniku makrotrhliny – kvazilineární chování průřezu,
- δ3,5 ≈ odpovídá průhybu při kterém lze zpravidla uvažovat plné zplastizování tažené i tlačené části průřezu.
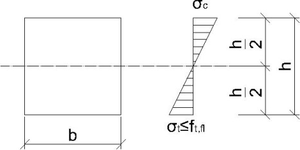
Pevnostní třída drátkobetonu je určena charakteristickými pevnostmi v tahu osovém. V případě vyčíslení těchto hodnot podle ČSN 73 2452 je třeba uvážit, že:
- U pevnosti v tahu při vzniku makrotrhliny provedené zkouškou trámců ohybem lze určit pouze pevnost v tahu za ohybu, kterou je nutné převést na pevnost v osovém tahu. V našem případě poděleným součinitelem γh,nom = 1,45, který respektuje tzv. „size effect“ zkoušený na trámcích výšky 150 mm.
- Pevnosti v tahu ve zvolených průhybech větších, než je průhyb, při kterém dochází ke vzniku makrotrhliny, lze již považovat vyčíslenou pevnost přímo za osovou pevnost v tahu, neboť tažená část průřezu je již zplastizována a závisí již pouze na únosnosti vláken, drátků procházejících trhlinou.
Z uvedeného tak vychází tahová pevnost za předpokladu, že FEk = FRk (Obr. 8).
Obr. 8 Napjatost průřezu normového trámce do vzniku makrotrhliny při kvazilineárně pružném chování
Obr. 9 Napjatost průřezu normového trámce po vzniku makrotrhliny při elasticko-plastickém chování
Vyčíslení pevnosti v tahu při vzniku makrotrhliny
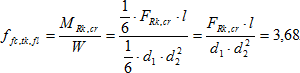(4)
[MPa]
Při uvážení:
d1 = d2 = 150 mm.
(5)
[MPa]
Vyčíslení pevnosti v tahu při dohodnutém mezním průhybu δt = 3,5 mm
Pevnost v tahu při dohodnutém mezním průhybu δt = 3,5 mm lze zpravidla uvážit, že obě části průřezu tažená i tlačená zplastizovaly, což znamená, že vyčíslenou tahovou pevnost lze považovat přímo za vyčíslenou tahovou pevnost v osovém tahu.
(6)
[MPa]
Pozn.: podle MC 2010 vychází 2,92 MPa, ale pro průhyb 2,5 mm.
3 Diskuse k vyčísleným charakteristikám
Vypočtené pevnosti drátkobetonu v tahu podle obou metodik jsou těžko porovnatelné při pohledu na jejich velikosti, zejména na kritéria stanovená pro jejich výpočet. Důvodem jsou též způsoby provedení zkoušek, úpravy zkušebních trámců a volené hranice, tj. jak šířky trhlin (MC 2010), tak i velikosti průhybu (ČSN 73 2452) z nichž se tahové pevnosti vyčíslují.
MC 2010 vychází z pevností určených CMOD 0,5, tj. při vzniku makrotrhliny, a neuvažuje tak vůbec pevnost, kterou je možné určit při vzniku makrotrhliny. Velikost pevnosti v tahu při rozevření trhliny w = 2,5 mm určuje jako 1/3 pevnosti stanovené v CMOD 3,5 za předpokladu pružného chování s přepočtem napětí, tj. převodu mezi napětím zjištěným za pružného chování a plně plastického chování drátkobetonového trámce.
ČSN 73 2452 naopak stanoví pevnost v tahu při vzniku makrotrhliny a pevnost při dosažení průhybu trámce δt = 3,5 mm podle uvedené normy při plně zplatizovaném průřezu.
4 Závěr
V příspěvku je ukázáno první srovnání MC 2010 a ČSN 73 2452 při zatřídění drátkobetonu do pevnostní třídy v tahu využitelné při návrhu drátkobetonových konstrukcí na mezní stav únosnosti.
Rozličné způsoby provádění průkazních zkoušek a jejich vyhodnocení vedou na rozdílné pevnosti drátkobetonu v tahu, jak je zřejmé při jejich porovnání.
Za zásadní rozdíly lze považovat:
- MC 2010 nepřihlíží k pevnosti v tahu při vzniku makrotrhliny a zjednodušený pracovní diagram uvažuje podle pevnosti v tahu prokázané u CMOD 2,5.
- Prokazování pevnosti v tahu při užití lineárního chování průřezu se nezcela slučuje se skutečnou představou napětí v průřezu při tvorbě trhlin.
- Metodiku zkoušení při tříbodovém uspořádání zatížení trámců s vytvořeným zářezem nezohledňuje důležitou charakteristiku vláknobetonu, tj. jejich homogenitu.
- ČSN 73 2452 plně respektuje při výpočtu tahových pevností napjatost ve zkušebních trámcích a zohledňuje homogenitu drátkobetonu namáháním střední části konstantním momentem.
- Pevnost při vzniku makrotrhliny považuje ČSN 73 2452 za důležitou při navrhování drátkobetonových konstrukcí bez možnosti připuštění trhlin, např. plně předpjaté drátkobetonové konstrukce.
- Zvolený průhyb trámků δt = 3,5 mm, tedy dle ČSN EN 14651 + A1 odpovídá přibližně rozevření trhliny wu = 4 mm lépe vyhovuje předpokladu plného zplastizování průřezu jak v tlačené, tak tažené oblasti, než zavedené rozevření trhliny w = 2,5 mm podle MC 2010.
Obě uvedené metodiky uvádí v originálech vztahy pro zpřesnění pracovních diagramů v oblasti mezi pružným a plastickým chováním průřezu, tj. respektují skutečnost, že dříve zplastizuje tažená část průřezu a v tlačené části průřezu je stále zachována linearita průběhu napětí.
5 Poděkování
Uvedený příspěvek byl zpracován za finanční podpory Technologické agentury České republiky (TAČR) TE1020168 a SGS15/036/OHK1/1T/11.
Literatura
- [1] TP FC 1-1 Technické podmínky 1: Vláknobeton – Část 1: Zkoušení vláknobetonu, vyhodnocení destruktivních zkoušek a stanovení charakteristického pracovního diagram vláknobetonu pro navrhování vláknobetonových konstrukcí; ČVUT v Praze, Fakulta stavební, Katedra betonových a zděných konstrukcí, Praha 2007;
- [2] ČSN EN 14651 + A1: Zkušební metoda betonu s kovovými vlákny – Měření pevnosti v tahu za ohybu (mez úměrnosti, zbytková pevnost); Český normaližační insitut, Listopad 2008;
- [3] Model Code 2010: Final draft Volume 1 + Volume 2; International Federation for Structural Concrete, March 2012;
Utilization of steel fibre reinforced concrete (SFRC) during the design of load-bearing structures presupposes that manufactured SFRC will be classified into the strength classes. For static design, these stated strength in the strength class are necessary: compression, tension when the macrocracks open and agreed limit deflection during the bending test on beams. The paper shows the procedure of determining the strength class of SFRC under such prescriptions. Different arrangement of the test equipment, differences in the ranges of test beams and their modifications affects the procedure for evaluation of tensile strength, including those resulting strength classes. Compressive strength of SFRC is considered in accordance with the evaluation of common (normal) concrete (cylinder/cube). These strength classes, calculated by two methodologies, show the difference in classification of one type of SFRC, in this case by increasing strength of SFRC after formation of the macrocrack caused by higher concentrate of fibres.
