Modelování podlahových dílců fasádních lešení

Hlavní výhodou dílcových fasádních lešení je jejich všestranná použitelnost bez nutnosti zvláštních úprav konstrukce. Tato výhoda se projeví zejména při montáži, která se tím výrazně urychlí a zpřesní. Pro běžná použití výrobce obvykle poskytuje montážní návod, který obsahuje veškeré údaje pro realizaci konstrukce lešení (kotevní rastr, zatěžovací třída apod.). Statický výpočet se provádí hlavně pro certifikaci systému lešení a pro komplikovanější provedení lešení, jako jsou nepravidelnosti sestavy, odskoky fasády, průjezdy, rozšíření podchodu podél objektu apod.

Statický návrh dílcových lešení patří mezi nejnáročnější procesy, hlavně kvůli výrazně nelineárnímu chování podlahových dílců, spojů apod. Pro návrh fasádních dílcových lešení se dnes používá norma ČSN EN 12 810-2 [1], kde je postup založen na kombinaci dvou rovinných modelů (tento postup byl již popsán v Lešenáři 13 [2]). Pro některé konstrukce (s komplikovanější dispozicí) je tento postup velmi těžko použitelný nebo časově velmi náročný a pro některé konfigurace není použitelný vůbec, proto se při praktickém navrhování téměř nepoužívá. Důsledkem je pak situace, kdy je atypické konfigurace lešení možné řešit jen nepřesně nebo nehospodárně. Tento problém by vyřešila možnost řešit tyto typy lešení lešení pomocí prostorových modelů. Jejich vytváření je však stále poměrně obtížné.

V průběhu doktorského studia, které autorka absolvovala na katedře ocelových a dřevěných konstrukcí fakulty stavební ČVUT v Praze, byl vytvořen model podlahového dílce, který zohledňuje nelineární chování lešení ve vodorovné rovině (rovině podlahy), a jako takový je použitelný do prostorového modelu fasádního rámového lešení.

Experimenty pro vývoj numerického modelu

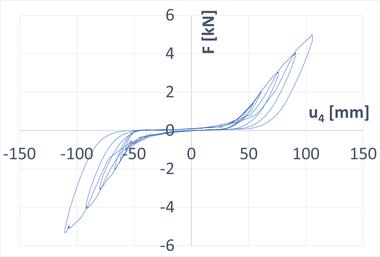
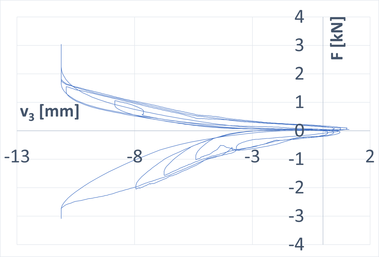
V rámci vývoje tohoto modelu byly provedeny experimenty na standardní základní sestavě lešení, která se skládala ze tří rámů lešení SPRINT 75. Byly provedeny zkoušky kolmo (obr. 1) a rovnoběžně s fasádou. Cílem těchto experimentů bylo co nejlépe popsat chování podlah lešení ve dvou vzájemně kolmých směrech (směr podélný a příčný) pro každou zkoušku. Standardní experimenty byly doplněny o další měřicí body, které zaznamenávaly posuny v kolmém směru na posuny předepsané normou [1].

Obr. 1: Fotografie ze zkoušky tuhosti podlahy lešení kolmo k fasádě

Výsledkem měření jsou potom grafy znázorňující závislosti posunů na působící síle. Na obr. 2 je zobrazen záznam měření posunů na prostředním sloupku pro zkoušku kolmo na fasádu.

Obr. 2: Záznam měření posunů u₄ (vlevo) a posunů v₃ (vpravo) na středním rámu

Naměřená dala byla dále upravována a vyhodnocována a převedena na střední hodnoty posunů v závislosti na působící síle. Pro vyhodnocení tuhostí podlahového systému lešení byla z těchto dat pomocí metody nejmenších čtverců odvozena matice tuhosti. Tato metoda je založena na principu minimalizace součtu reziduálních čtverců a používá se u soustav rovnic, kde je více neznámých než rovnic.

Pro určení tuhosti numerického modelu, byly obě zkoušky (kolmo a rovnoběžně s fasádou) simulovány pomocí rovinné příhradové konstrukce. V modelu se uvažují dva neznámé parametry, a to tuhosti diagonál k_D1 a k_D2.

Numerický model má tvar

(1)

kde je matice tuhosti závislá na dvou neznámých tuhostech diagonál, je vektor uzlových posunutí a vektor předepsaných uzlových sil. K určení tuhosti diagonál se použila metoda nejmenších čtverců, která minimalizovala funkci

(2)

Po úpravě a zjednodušení jsou zde uvedené výsledné rovnice (3) a (4), které představují soustavu dvou algebraických rovnic pro dvě neznámé k_D1 a k_D2 a mají tvar

(3)

(4)

kde a jsou uzlová posunutí a síly v i-tém odečtu, n je počet odečtů během zkoušky. Řešením těchto rovnic se získají odhady tuhostí diagonál v rovinném příhradovém modelu podlážky v jednom poli lešení.

Model podlahových dílců

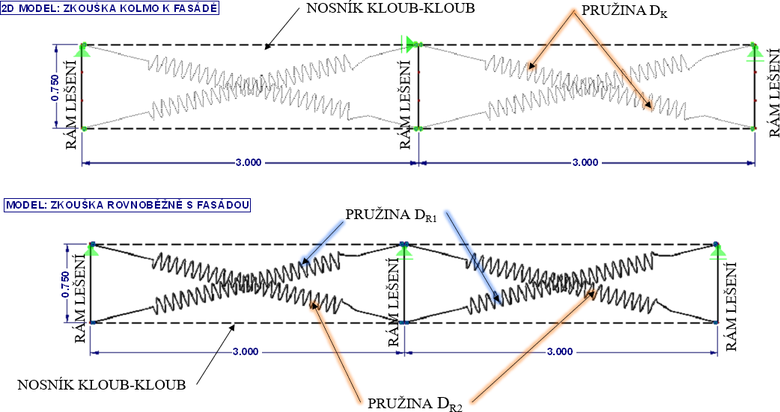
V prvním kroku byly nejprve vytvořeny rovinné modely pro každou provedenou zkoušku zvlášť (modely kolmo k fasádě a modely rovnoběžně s fasádou) (obr. 3). Modely byly vytvořeny v inženýrském softwaru RFEM 5 od společnosti Dlubal. Tyto prutové modely sestávají z dvou typů nosníků: nosník, který představuje rám systémového lešení a nosník typu kloub-kloub, který propojuje jednotlivé rámy v rovině podlahy. Mezi těmito nosníky v úrovni podlahy jsou umístěny pružiny, které svojí nadefinovanou tuhostí a vůlí simulují nelineární chování lešeňové sestavy v rovině podlahy. Zelené kloubové podpory představují podepření lešení v průběhu zkoušky tuhosti podlah. Model tvarem i rozměry odpovídá provedeným zkouškám.

Obr. 3: Půdorysné schéma 2D modelů

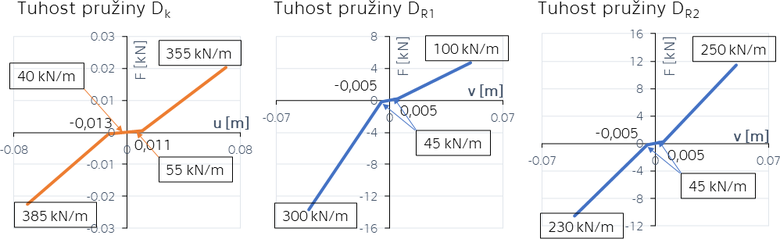
Modely byly následně validovány. Validace modelů spočívala v cílených úpravách průběhů nelineárních tuhostí v obou směrech tak, aby se výsledky výpočtů co nejvíce přiblížily experimentům. V rámci validace byla provedena linearizace jednotlivých částí pracovních diagramů modelů v obou směrech. Výsledné tuhosti pro oba modely jsou na obr. 4. Jak je patrné ze schémat rovinných modelů (obr. 3), pro rovinu ve směru kolmo na fasádu mají všechny pružiny stejné nastavení a tuhost je uvedena na obr. 4 vlevo – pružina D_K. Na obr. 4 uprostřed a vpravo jsou odvozené tuhosti pro rovinu rovnoběžně s fasádou, pružiny D_R1 a D_R2.

Obr. 4: Tuhosti pružin podlahového dílce

Po úspěšné validaci rovinných modelů byly tyto modely transformovány do jediného rovinného modelu. Oba systémy byly propojeny a okrajové podmínky nastaveny tak, aby pro jednotlivé směry zatěžování působila pouze příslušná část modelu. Na obr. 5 je prostorový model podlahového dílce s propojením rovin. Podlahový dílec se nachází v rovině x-y souřadného systému x-y-z.

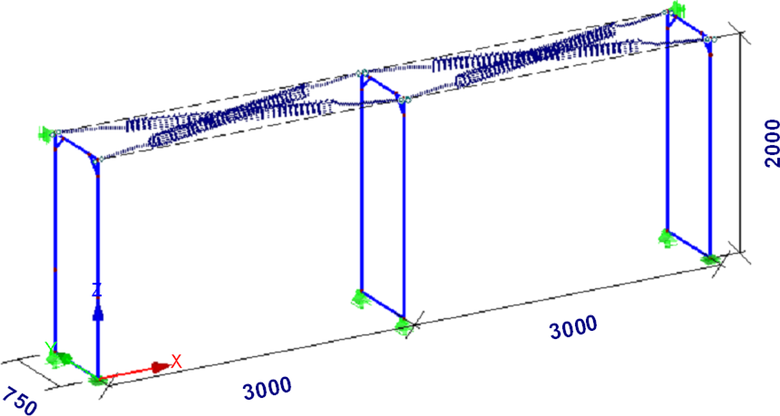
Obr. 5: Prostorový model lešeňové sestavy se třemi rámy

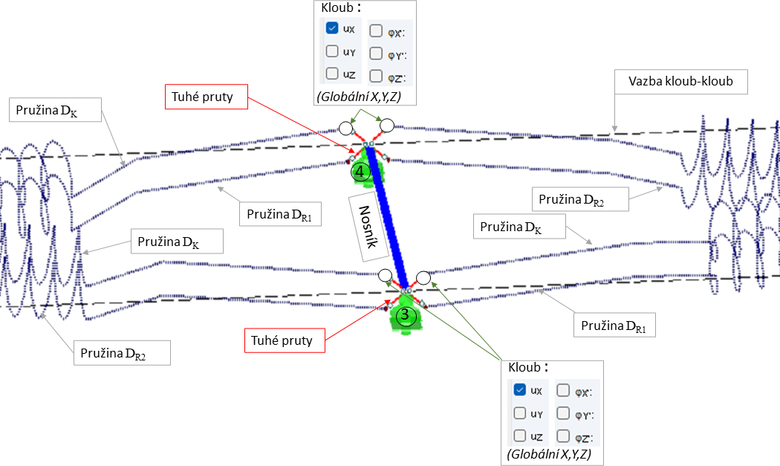
Na obr. 6 je detail připojení rovin podlahy se znázorněným nastavením okrajových podmínek pro roviny působící kolmo na fasádu a rovnoběžně s fasádou. Okrajové podmínky prutů jsou nastaveny pomocí kloubů na konci prutu. U každého kloubu jsou opět znázorněny odpovídající podporové podmínky. Čárkovaně je znázorněna vazba „kloub-kloub“. Jedná se o tuhé spojeni s kloubovým připojením na obou koncích prutu a propojuje podlahové roviny s rámy. Podlahové roviny jsou připojeny k nosníku pomocí „tuhého prutu“ (červená čárkovaná čára). Tento typ prutu se ve výpočtu svojí tuhostí přizpůsobí zbytku konstrukce. Pomocí kloubů na konci prutu jsou pro rovinu nastaveny příslušné okrajové podmínky.

Jak je z detailu patrné (obr. 6), rovina rovnoběžně s fasádou je připojena k nosníku (příčníku rámu) tuze pomocí „tuhého prutu“. Rovina pro směr kolmo k fasádě je rovněž připojena pomocí „tuhého prutu“, ten je na konci opatřen „vnitřním kloubem“. Kvůli zajištění numerické stability modelu musela být nastavena (minimální) tuhost kloubu na konci tuhého prutu.

Obr. 6: Detail připojení podlahového systému na střední nosník (příčník rámu)

Závěr

Výsledný model podlahy, který zohledňuje odlišné chování v obou vodorovných směrech, bude sloužit jako komponenta univerzálně použitelná v prostorovém prutovém modelu libovolné sestavy fasádního lešení. Metodika je použitelná i pro obdobné typy podlahových dílců. Vždy je ovšem nezbytné nejprve provést zkoušku na standardní základní sestavě lešení o dvou polích.

Oznámení

Prezentovaný výzkum je podporován mj. Technologickou agenturou České republiky, projektem TJ04000305. Autoři tuto podporu vysoce oceňují.

Literatura

1. ČSN EN 12 810-2 (73 8111): Fasádní dílcová lešení – Část 2: Zvláštní postupy při navrhování konstrukce. ČNI 2004.
2. Lešenář 13, ISSN 2464-5338; ČMKL 2017.