Nejistota výsledků měření při zkouškách
Článek stručně uvádí základní odbornou terminologii, chyby a výpočetní algoritmy odhadu nejistot typu A, typu B, kombinované a rozšířené nejistoty výsledků naměřených při zkouškách, zdůrazňuje nezbytnost, aby obsluha zkušebních zařízení a měřidel měla potřebné teoretické znalosti a management zkoušek plnil úkoly specifikované normou ČSN EN ISO/IEC 17025.
Úvod
Výsledky měření/zkušebních stanovení jsou závislé nejenom na vlastnostech předmětu zkoušek, ale též na množství jiných ovlivňujících faktorů. Proto se zkoušky mezinárodně standardizují, tj. sjednocují se konstrukce zkušebních zařízení, zkušební postupy, zkušební podmínky, způsob vyhodnocení a vyjádření naměřených hodnot, přepočet na standardní stav, meze opakovatelnosti a reprodukovatelnosti, verifikace přístroje, validace zkušebních metod atd.
Nedílnou součástí je odborná terminologie z oblasti matematické statistiky a pravděpodobnosti, přesnosti, pravdivosti, preciznosti zkušebních metod, postupy ověřování způsobilosti laboratoří, postupy stanovení a posouzení nejistot, zajišťování stability výsledků měření, postupy kalibrací, postupy validace metod a v neposlední řadě kvalita vzorkování.
Znalost nejistoty zkušebních výsledků měření má v současné době velkou důležitost jak pro zkušební laboratoře, tak pro zadavatele zkoušek – uživatele výsledků a výrobce materiálových výrobků. Nejistota výsledků je tak velmi důležitou mírou kvality výsledků zkoušek/měření a návazných interpretací výsledků. Před praktickou aplikací výsledků zkoušek/měření musí proto laboratoř a jejich uživatelé mít jasno, jak přesné tyto výsledky jsou. Analýza chyb musí být nedílnou součástí měření při zkouškách.
V plné míře to platí i pro obor stavebnictví kde se testují na stavebních materiálech/výrobcích např. rozměry, hustoty, pevnosti v tahu, tlaku, ohybu, meze pevnosti, přídržnosti, soudržnosti, moduly pevnosti, tvrdosti, konzistence, obsah vzduchu, obsah sušiny, mrazuvzdornost, nasákavost, absorpce vody, vodotěsnost, další fyzikální a mechanické vlastnosti podle platných zkušebních norem ČSN, ČSN EN, ČSN EN ISO, DIN, IEC, ČSN IEC, ANSI WTA, atd.
Pro potřebu čtenářů k podrobnějšímu seznámení je proto v Literatuře též uveden přehled dotčených mezinárodních norem ISO, IEC, EN a ČSN a předpisů EAL a EGOLF, které dotčenou problematiku řeší v dalších souvislostech.
1. Terminologie
Obsluha provádějící zkušební stanovení musí ovládat související odbornou terminologii, aby správně mj. interpretovala své výsledky. Mezi ty základní patří zejména [20 a 33]:
- chyba výsledku (error of result): rozdíl mezi výsledkem zkoušky a přijatou referenční hodnotou,
- přesnost (accuracy): těsnost shody mezi výsledkem zkoušky a přijatou referenční hodnotou,
- správnost/pravdivost (trueness): těsnost shody mezi průměrnou hodnotou získanou z velké řady výsledků zkoušek a přijatou referenční hodnotou,
- shodnost/precisnost (precision): těsnost shody mezi nezávislými výsledky zkoušek získanými za předem specifikovaných podmínek. Závisí pouze na rozdělení náhodných chyb. Vyjadřuje se směrodatnou odchylkou,
- strannost/vychýlení (bias): rozdíl mezi střední hodnotou výsledků zkoušek a přijatou referenční hodnotou. Je to celková systematická chyba v protikladu k náhodné chybě,
- opakovatelnost (repeatability): shodnost za podmínek opakovatelnosti,
- podmínky opakovatelnosti (repeatability conditions): podmínky za kterých se získají výsledky zkoušky stejnou metodou, na stejném zkušebním a měřicím zařízení, v téže laboratoři, stejnou obsluhou a běhen krátkého časového rozmezí,
- mez opakovatelnosti (repeatability limit, r): hodnota, o níž se předpokládá, že pod ní bude ležet nebo se jí rovnat absolutní hodnota rozdílu mezi dvěma výsledky zkoušek za podmínek opakovatelnosti, a to s pravděpodobností 95 %,
- reprodukovatelnost (reproducibility): shodnost za podmínek reprodukovatelnosti,
- podmínky reprodukovatelnosti (reproducibility conditions): podmínky za kterých se získají výsledky zkoušky stejnou metodou, na stejném zkušebním a měřicím zařízeních, ale v různých laboratořích, různými obsluhami a běhen delšího časového rozmezí,
- mez reprodukovatelnosti (reproducibility limit, R): hodnota, o níž se předpokládá, že pod ní bude ležet nebo se jí rovnat absolutní hodnota rozdílu mezi dvěma výsledky zkoušek za podmínek reprodukovatelnosti, a to s pravděpodobností 95 %,
- nejistota (uncertainty): číselný odhad přiřazený k výsledku zkoušky a charakterizující interval hodnot, o němž se tvrdí, že uvnitř něho leží správná hodnota.
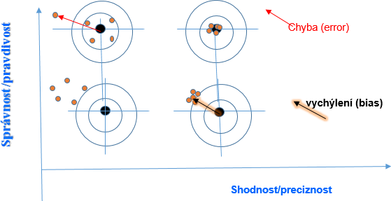
Uvedenou definici správnosti, shodnosti a přesnosti výsledků měření/zkoušky názorně zobrazuje obr. č. 1.
Poznámka: Referenční výsledek je uprostřed terče. Výsledek, na který ukazuje červená šipka, je zjevně chybný. Výsledky na druhém terči jsou správné, shodné a přesné, na třetím terči nesprávné a nepřesné, na čtvrtém terči vychýlené, ale shodné.
2. Chyby a nejistoty výsledků zkoušek
2.1 Chyby a jejich příčiny
Bylo zvykem vyhodnocovat u naměřených hodnot jejich chyby v absolutní nebo relativní formě. Podle místa vzniku je lze členit na instrumentální, metodické, teoretické a na chyby zpracování.
Podle příčin jsou tříděny na:
- náhodné: při opakovaném měření náhodně kolísají co do velikosti a znaménka, mají specifické rozdělení pravděpodobnosti a nelze je eliminovat. Výsledek měření z opakovaných měření za podmínek opakovatelnosti je odhadován výběrovým aritmetickým průměrem y̅, náhodnou odchylkou /chybou shodnosti) oi, rozptylem s2(yi) nebo směrodatnou odchylkou jednotlivého měření s (yi) a výběrového aritmetického průměru sy̅ :
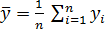 (1)
(1)
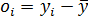 (2)
(2)
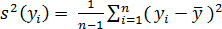 (3)
(3)
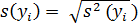 (4)
(4)
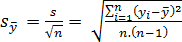 (5)
(5)
- systematické: mívají stejné znaménko a obvykle i stejnou hodnotu při opakovaném měření. Podrobněji se člení na: aditivní (v důsledku špatného nastavení nuly), multiplikativní (chyba např. v citlivosti) a hrubé.
- hrubé: chyby tzv. vybočující nebo odlehlé. Jejich příčinou je hrubá chyba, např. porucha na části zařízení nebo chyba obsluhy. Silně by znehodnotily výsledek, a proto musí být statisticky potvrzeny (hodnocení vybočených a odlehlých hodnot (Cochranův a Dean-Dixonův test) a dotčené výsledky měření následně vyloučeny z výsledného hodnocení.
2.2 Model měření a nejistoty výsledků
Postup odhadu nejistot schematicky znázorňuje obr. č. 2.
Vlastnímu vyhodnocení nejistoty výsledku měření/zkoušky musí předcházet znalost modelu měření. V řadě případů není zkušebně měřená/stanovovaná veličina Y měřená přímo, ale stanovuje se obecně z n různých vstupních veličin X1, X2, …, Xi, P, Q, R, …, které mohou mít funkční vztahy
V řadě případů je nejlepším odhadem Xi výběrový aritmetický průměr x̅i, vypočtený podle rovnice (1) z n naměřených hodnot xij (j = 1 až n) paralelním měřením. Měřené veličiny Xi jsou většinou náhodné veličiny s určitým rozdělením pravděpodobnosti odchylek (normálním, obdélníkovým, trojúhelníkovým, atd., viz tab. č. 1 a obr. č. 3 a č. 4 níže), charakterizovaných hustotou pravděpodobnosti f(x), distribuční funkcí F(x) a parametry, charakterizujícími rozptýlení tohoto rozdělení. Základní charakteristikou odhady polohy středu je výběrový aritmetický průměr a rozptýlení buď výběrový rozptyl, výběrová směrodatná odchylka, nebo výběrový variační koeficient či výběrové rozpětí. Nejistoty měření se obecně člení podle způsobu odhadu.
2.2.1 Nejistota typu A, uA
Odhaduje se statistickou analýzou z opakovaných měření za podmínek opakovatelnosti obvykle směrodatnou odchylkou výběrového průměru, např. uxi,A = sxi vypočtenou z rozptylu nebo rozpětí.
2.2.2 Nejistota typu B, uB
Postup odhadu lze stručně charakterizovat následujícími kroky:
- identifikací zdrojů: mezi systematické zdroje patří např.:
- nesprávné vzorkování,
- neznalost podmínek okolí,
- nepřesné odečty z přístrojů obsluhou,
- nízká rozlišitelnost stupnic měřicích přístrojů,
- nízká citlivost přístrojů,
- chyby ve výpočtech,
- kvantifikací nejistot od jednotlivých zdrojů, uxi
- kalibrace přístrojů dává znalost jejich kombinované nejistoty podle kalibračních listů,
- odhadnou se maximální rozpětí ΔZmax u dotčených veličin a u nich pravděpodobné rozdělení odchylek s následným odhadem uziB podle vzorce
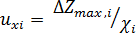 (6)
(6)
když χi se určí podle typu rozdělení dle tab. č. 1.
Při provádění měření a uvádění výsledků a jejich využívání musí dodavatel vzít v úvahu všechny závažné nejistoty v procesu měření včetně těch, k nimž přispívají individuální postupy pracovníků a vlivy okolního prostředí. Pro průběžné sledování nejistoty měření se doporučuje užívání statistických metod (ČSN ISO 9004 [59]).
Tab. č. 1 Vybrané charakteristiky rozdělení pravděpodobnosti Di prakticky používaných při odhadu nejistoty typu B Di f(Δz) = µ s χ kp = Obdélníkové = 1/2a pro µ − a < Δz ≤ µ + a
= 0 jinakµ a/ 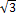
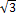
= 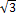 .p
.pTrojúhelníkové = (1/a2).(Δz − µ + a) pro µ − a < Δz ≤ µ
= (1/a2).(µ + a − Δz) pro µ < Δz ≤ µ + aµ a/ 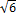
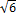
= 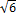 .(1 −
.(1 − 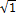 − p)
− p)Trojúhelníkové bimodální = 0 pro Δz ≤ µ − a
= (1/a2).(Δz − µ) pro µ − a < Δz ≤ µ
= (1/a2).(µ − Δz) pro µ < Δz ≤ µ + a
= 0 pro Δz > µ + aµ a/ 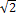
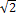
= 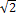 .p
.pGaussovo normální = 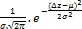
pro µ − a < Δz ≤ µ + aµ a/3 3 = 3p Vysvětlivka:
- f(Δz)
- – hustota pravděpodobnosti,
- µ
- – střední hodnota,
- χ
- – kritérium rozdělení jako poměr mezní odchylky ke směrodatné odchylce pro vybraný typ rozdělení,
- kp
- – koeficient rozšíření – číselný faktor, kterým se násobí kombinovaná standardní nejistota výsledku měření pro výpočet rozšířené nejistoty, tj. veličiny kvantifikující interval kolem výsledku měření, ve kterém se bude nacházet správná hodnota výsledku s příslušnou pravděpodobností (např. pro k = 2 u normálního rozdělení je to pravděpodobnost 95 %.)
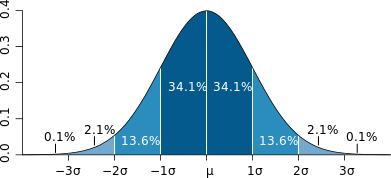
Směrodatná odchylka od střední hodnoty µ naměřených výsledků
Obr. 3 Příklad Gaussova (normálního) rozděleníZ grafu je patrno, že uvnitř směrodatných odchylek: ±1 leží 68,2 % výsledků, ±2 leží 95,4 % výsledků a ±3 leží 99,8 % výsledků.
- posouzením možné korelace mezi jednotlivými zdroji Zi a odhad jejich korelačních koeficientů riZ :
při přímém měření jedné veličiny lze po ověření předpokládat, že korelace mezi jednotlivými zdroji nejistoty typu B je zanedbatelná. Pokud vstupní veličiny x1, x2, …., xi nejsou nezávislé, tj. jsou korelovány, musí se výpočetně odhadnout jejich výběrová kovariance u (xi, xj), a příslušný výběrový korelační koeficient r (xi, xj) se musí odhadnout podle vzorců:
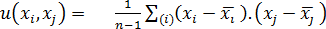 (7)
(7)
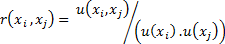 (8)
(8)
když xi a xj jsou nezávislé páry simultánního měření.
2.2.3 Standardní kombinovaná nejistota uc(y)
Kombinovaná standardní nejistota uc(y) se rovná druhé odmocnině kombinovaného rozptylu uc2 (y) ze součtu rozptylů vstupních veličin a případně všech kovariancí. Přicházejí v úvahu dvě možnosti:
- jsou-li vstupní veličiny nezávislé, má standardní kombinovaná nejistota tvar
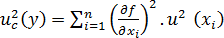 (9)
(9)
když veličina Y je vyjádřena vztahem (3) a každá standardní nejistota uxi je určena buď postupem A, nebo postupem B, - jsou-li vstupní veličiny korelovány, potom
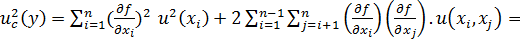 (10)
(10)
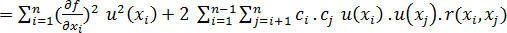
když u (xi, xj) je kovariance mezi xi a xj
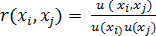 je korelační koeficient
(11)
je korelační koeficient
(11)
Platí další dvě pravidla pro slučování nejistot:
- pro funkční závislost aditivního charakteru typu y = k. (p + q + r +…), kde k je konstanta, lze odhadnout kombinovanou standardní nejistotu z rov. (12)
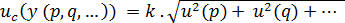 (12)
(12)
- pro funkční závislost multiplikativního charakteru, např. typu y = k. (p.q.r...) a kde k je opět konstanta, lze odhadnout kombinovanou standardní nejistotu z rov. (13)
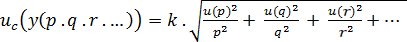 (13)
(13)
2.2.4 Rozšířená nejistota U
Výpočetní odhad spočívá ve vynásobení kombinované nejistoty uc (y) tzv. koeficientem pokrytí (rozšíření) k podle vzorce
když koeficient pokrytí k závisí na hladině pravděpodobnosti pokrytí p s konfidenční úrovní (1 − α). Konfidenční úrovni 95 % odpovídá k = 2 a úrovni 99 %, k = 3 pro normované normální rozdělení.
2.2.5 Relativní nejistota Ur
Pokud někdo upřednostňuje vyjádření nejistot v relativních hodnotách, lze jednoduše vyjádřit podle následujících vzorců:
- relativní citlivostní koeficient:
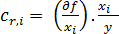 (15)
(15)
- relativní kombinovanou standardní nejistotu:
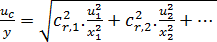 (16)
(16)
- relativní rozšířenou nejistotu:
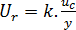 (17)
(17)
Závěr
Mezinárodně akceptované postupy stanovení nejistoty výsledků měření/zkoušek jsou v rámci ČR úspěšně realizovány a interpretovány v akreditovaných zkušebních a kalibračních laboratořích ustanovených a dozorovaných Českým institutem pro akreditaci. Nicméně i neakreditované zkušební a výzkumné laboratoře by měly aplikovat principy managementu, politiky jakosti, vedení záznamů z měření/zkoušek a vyhodnocování nejistot kvantitativních a kvalitativních výsledků atd. v souladu s ČSN EN ISO/IEC 17025 [10] a dalšími dotčenými normami.
Platné postupy odhadu nejistot včetně statistických metod řízení procesů musí aplikovat odborně erudovaní pracovníci. Je v zájmu managementu laboratoře, aby mj. kvalita měření/zkoušek byla systematicky plánována, organizována a kontrolována včetně kalibrací měřidel, validace interních zkušebních metod a pravidelné verifikace funkčnosti zkušebních zařízení a správnosti provádění normových zkušebních postupů interně nebo účastí v mezilaboratorních porovnávacích/kruhových zkouškách (MPZ/RRT).
Verifikace by neměla být omezována jenom k ověření aktualizovaných zkušebních norem (nová vydání, opravy, doplňky), ale též v průběhu jejich platnosti k prokázání, že zkušební zařízení a měřidla jsou funkční a že pověření pracovníci ke zkouškám správně realizují normový postup zkoušek s potřebnou přesností (accuracy), správností (trueness) a shodností (precision), což zahrnuje i nejistotu výsledků.
Literatura
I. Vybrané normy z oblasti nejistot měření a zkoušení
- ČSN P ISO/TS 21748:2005 Návod pro použití odhadů opakovatelnosti, reprodukovatelnosti a správnosti při odhadování nejistoty měření.
- Guide to the expression of uncertainty in measurement (GUM). Vydaly: BIPM / IEC / IFCC / ISO / IUPAC / IUPAP / OIML 1993, reedice 1995.
- ČSN ISO 21749 Measurement and uncertainty for metrological applications – Repeated measurements and nested experiments (Nejistoty měření v metrologických aplikacích – Opakovaná měření a hierarchické experimenty).
- NORDTEST TR 537: 2003 Handbook for calculation of measurement uncertainty in environmental laboratories (Příručka pro výpočet nejistot měření v laboratořích působících v oblasti životního prostředí).
- EAL 4/02 Expression of the uncertainty of measurement in calibration (Vyjadřování nejistot měření při kalibracích).
- EURACHEM/CITAC Quantifying uncertainty in analytical measurement (Číselné vyjadřování nejistot analytického měření).
- ČSN EN ISO 12999-1:2015 Akustika – Určování a používání nejistot měření ve stavební akustice – Část 1: Zvuková izolace.
- EAL – G23 Vyjadřování nejistot v kvantitativním zkoušení“: čl. 10 „Výsledek měření by měl být uveden spolu s přiřazenou rozšířenou nejistotou, odpovídající 95% intervalu spolehlivosti.
- EGOLF/TC4, document No. 55 Guidelines for interpretation of EN 45001 for fire test laboratories and for accreditators of fire test laboratories.
- ČSN EN ISO/IEC 17025 Posuzování shody – Všeobecné požadavky na způsobilost zkušebních a kalibračních laboratoří.
- Analýza systémů měření (MSA). Vydaly ASQC a AIAG, druhé vydání 1995 – český překlad ČSJ v roce 1999.
- Analýza systémů měření (MSA). Vydaly ASQC a AIAG, třetí vydání 2002 – český překlad ČSJ v roce 2003.
- Report of ISO/TC69/SC6/WG7/N377(May 1998) Relationship between ISO 5725 and ISO Guide to the Expression of Uncertainty in Measurement.
- Sborník ÚNMZ: Nejistoty měření, přesnost měření, správnost měření, uvádění nejistot měření a otázky spojené s prohlášením o shodě s technickými specifikacemi v legální metrologii (autor V. Ludvík), 2005.
- ČSN ISO 45001: 2018 Systémy managementu kvality a ochrany zdraví při práci – Požadavky s návodem použití.
- ČSN EN ISO 10012: 2003 Systémy managementu měření – Požadavky na procesy měření a měřicí vybavení.
II. Základní a terminologické normy
- ČSN 01 0115:1996 Mezinárodní slovník základních a všeobecných termínů v metrologii.
- VIM:1993:1996 Mezinárodní slovník základních a všeobecných termínů v metrologii. Vydaly: BIPM, IEC, IFCC, ISO, IUPAC, OIML). Byl převzat do ČSN 01 0115.
- ČSN ISO 3534-1:1994 Statistika – Slovník a značky. Část 1:Pravděpodobnost a obecné statistické termíny.
- ČSN ISO 3534-2:1994 Statistika – Slovník a značky. Část 2: Statistické řízení jakosti.
- ČSN ISO 3534-3:2001 Statistika – Slovník a značky. Část 1: Navrhování experimentů.
- ČSN EN ISO 9000:2001 Systémy managementu jakosti – Základy, zásady a slovník.
III. Normy z oblastí aplikované statistiky, statistické interpretace údajů, metod a výsledků měření
- ČSN ISO 2602:1993 Statistická interpretace výsledků a zkoušek – Odhad průměru – Konfidenční interval.
- ČSN ISO 2854:1994 Statistická interpretace údajů – Odhady a testy středních hodnot a rozptylů.
- ČSN ISO 3207:1993 Statistická interpretace údajů – Stanovení statistického tolerančního intervalu.
- ČSN ISO 3301:1993 Statistická interpretace údajů – Porovnání dvou průměrů v případě párových pozorování.
- ČSN ISO 5479:1998 Statistická interpretace údajů – Testy odchýlení od normálního rozdělení.
- ČSN ISO 10576-1:2004 Statistické metody – Směrnice pro hodnocení shody se specifikovanými požadavky – Část 1: Obecné principy.
- ČSN ISO 16269-7:2002 Statistický interpretace údajů – Část 7: Medián – Odhad a konfidenční intervaly.
- ČSN ISO 16269-8:2005 Statistická interpretace údajů – Část 8: Stanovení předpovědních intervalů.
- TNI 01 4109 – 1: 2011 Nejistota měření – Část 1: Úvod k vyjadřování nejistot měření (pokyn ISO/IEC 98-1).
- TNI 01 4109 – 3: 2011 Nejistota měření – Část 3: Postup pro vyjádření nejistoty měření (GUM 1995, pokyn ISO/IEC 98-3).
- TNI 01 4109 – 4: 2011 Nejistota měření – Část 4: Úloha nejistoty měření při posuzování shody.
IV. Normy z oblastí přesnosti metod, opakovatelnosti, reprodukovatelnosti, správnosti
- ČSN ISO 5725-1:1997 Přesnost (správnost a shodnost) metod a výsledků měření – Část 1: Obecné zásady a definice.
- ČSN ISO 5725-2:1997 Přesnost (správnost a shodnost) metod a výsledků měření – Část 2: Základní metoda pro stanovení opakovatelnosti a reprodukovatelnosti normalizované metody měření.
- ČSN ISO 5725-3:1997 Přesnost (správnost a shodnost) metod a výsledků měření – Část 3: Mezilehlé míry shodnosti normalizované metody měření.
- ČSN ISO 5725-4:1997 Přesnost (správnost a shodnost) metod a výsledků měření – Část 4: Základní metody pro stanovení správnosti normalizované metody měření.
- ČSN ISO 5725-5:1999 Přesnost (správnost a shodnost) metod a výsledků měření – Část 5: Alternativní metody pro stanovení shodnosti normalizované metody měření.
- ČSN ISO 5725-6:1997 Přesnost (správnost a shodnost) metod a výsledků měření – Část 6: Použití hodnot měr přesnosti v praxi.
V. Normy z oblastí detekční schopnosti a kalibrace
- ČSN ISO 11095:1997 Lineární kalibrace s použitím referenčních materiálů.
- ČSN ISO 11843-1:1998 Detekční schopnost – Část 1: Termíny a definice.
- ČSN ISO 11843-2:2001 Detekční schopnost – Část 2: Metodologie v případě lineární kalibrace.
- ČSN ISO 11843-3:2004 Detekční schopnost – Část 3: Metodologie pro stanovení kritické hodnoty odezvy bez použití dat z kalibrace.
- ČSN ISO 11843-4:2004 Detekční schopnost – Část 4: Metodologie pro porovnání minimální detekovatelné hodnoty s danou hodnotou.
VI. Normy z oblastí regulačních metod a kontroly stability výsledků zkoušek
- ČSN 01 0266:1987 Zvláštní typy statistické regulace – Metoda kumulovaných součtů.
- ČSN ISO 5725-6:1997 Přesnost (správnost a shodnost) metod a výsledků měření – Část 6: Použití měr přesnosti v praxi.
- ISO/TR 7871:1997 Diagramy pro metodu kumulovaných součtů – Návod k řízení jakosti a analýze pomocí metody CUSUM (technická zpráva ISO není přeložena do češtiny).
- ČSN ISO 7873:1995 Regulační diagramy pro aritmetický průměr s výstražnými mezemi.
- ČSN ISO 7966:1995 Přejímací regulační diagramy.
- ČSN ISO 8258:1994 Shewhartovy regulační diagramy.
VII. Normy z oblasti vzorkování hromadných materiálů
- ČSN ISO 10725:2002 Výběrové přejímací plány a postupy pro kontrolu hromadných materiálů.
- ČSN ISO 11648-1:2004 Statistická hlediska vzorkování hromadných materiálů – Část 1: Obecné principy
- ČSN ISO 11648-21:2003 Statistická hlediska vzorkování hromadných materiálů – Část 2: Vzorkování sypkých materiálů.
VIII. Související
- Zákon č. 22/1997 Sb., ze dne 24. ledna 1997 o technických požadavcích na výrobky a o změně a doplnění některých zákonů ve znění pozdějších předpisů.
- Nařízení vlády č. 163/2002 Sb., ze dne 6. března 2002, kterým se stanoví technické požadavky na vybrané stavební výrobky, ve znění pozdějších předpisů.
- Nařízení Evropského parlamentu a Rady (EU) č. 305/2011 ze dne 9. března 2011, kterým se stanoví harmonizované podmínky pro uvádění stavebních výrobků na trh, a kterým se zrušuje směrnice Rady 89/106/EHS, ve znění po opravě zveřejněné.
- MELOUN, M., MILITKÝ, J. Statistické zpracování experimentálních dat. Praha: PLUS, 1994.
- DVOŘÁK, O. Statistické posouzení kvantitativních jakostních parametrů stavebních výrobků při posuzování shody a certifikaci v oblasti požární ochrany. Časopis TZB-info, 30. 11. 2015.
- ČSN EN ISO 9004:2019 Management kvality – Kvalita organizace – Návod k dosažení udržitelného výsledku.
Článek se zabývá aktuální tématikou vyhodnocení nejistot pokusných dat, např. závěrů z chemických analýz nebo pevnostních měření stavebních materiálů. Autor vychází ze současného stavu problematiky a shrnuje definice nejistot typu A i B a výpočetní postupy pro ně za předpokladů různých modelů mezi přímo měřenými veličinami a hledanou veličinou (aditivní, multiplikativní). Uvádí rovněž definiční vztahy pro tři základní rozdělení pravděpodobnosti odchylek (normální, uniformní, trojúhelníkové). Pokud by čtenáři k vlastnímu využití nestačily informace v článku, může se snadno obrátit k uvedenému rozsáhlému seznamu literatury, převážně platných norem. Článek je vysoce aktuální a doporučuji jej k uveřejnění.
The article briefly introduces basic technical terminology, errors and computational algorithms for estimating uncertainty of type A, type B, combined and extended uncertainty of test results and that the test management performs the tasks specified in the standard ČSN EN ISO / IEC 17025.
![Obr. 2 Blokové schéma odhadu nejistoty měření podle GUM [2]](/docu/clanky/0199/019912o9.jpg)
![Obr. 4a Příklad pravoúhelného rozdělení pravděpodobnosti [2]](/docu/clanky/0199/019912o18.png)
![Obr. 4b Příklad trojúhelníkového rozdělení pravděpodobnosti [2]](/docu/clanky/0199/019912o20.png)