Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Stanovení svislých sil od zatížení dřevěné výškové budovy

Ing. Luděk Vejvara, Ph.D., Západočeská univerzita v Plzni, Katedra mechaniky

Recenzovaný

Velikost působícího zatížení na stěny vysokých dřevěných staveb lze podle stávajících norem sestavit dle platných kombinačních rovnic více způsoby. Existují tak rozdíly mezi výsledky. Vymezení vhodného postupu stanovení svislé síly od stavby v různých částech přípravy stavby a jeho porovnání s dalšími možnostmi je předmětem tohoto příspěvku.

1. Popis problému

Zatížení staveb obecně sestavujeme podle platných norem – eurokódů. Platí tak i u vysokých dřevěných staveb. K stanovení velikosti stálých používáme údaje o rozměrech a popisu konstrukcí z projektů a údaje o objemové hmotnosti z normy ČSN EN 1991-1-1. Proměnná zatížení na podlahách stanovujeme podle určení prostor ve stavbě podle ČSN EN 1991-1-1.

Kombinace stálých a proměnných zatížení stanovujeme podle normy ČSN EN 1990. Pro mezní stav únosnosti stanovujeme hodnoty zatížení pro následující stavy: EQU, STR a pro seismické a mimořádné návrhové situace. Pro mezní stavy použitelnosti určujeme hodnoty zatížení pro charakteristické, kvazistálé a časté kombinace zatížení. Podrobnými výpočty tak získáme v daném místě konstrukce řadu hodnot, které reprezentují mezní návrhové zatížení a také provozní nebo minimální účinky. Přitom jen pro mezní stav STR (ev. GEO) má statik k volbě nejméně 3 postupy podle platných rovnic s různými výsledky svislé síly v místě nejvíce zatíženého svislého prvku, což vede k různým profilů a řešením dřevěné konstrukce. Dále to má vliv i na návrh a velikost základů pro tuto konstrukci. Často je užívána nejjednodušší forma výpočtu podle rovnice STR/GEO 6.10 (viz další text). Toto řešení je sice nejbezpečnější, ale také s největší silou, tj. je nejkonzervativnější a nejméně ekonomické. Přináší méně práce než ostatní způsoby. Ale je třeba říci, že někdy je i tak počet rozvinutých kombinací ve výpočtech v programech velký. Přesto by volba pro stavbu ekonomického postupu návrhu měla být výhodná, a to zejména pro investora a při zpřesnění konstrukce v prováděcí dokumentaci.

2. Možná řešení k určení velikosti svislé síly

Pro sestavení působící svislé síly v mezním stavu únosnosti STR používáme rovnice uvedené v ČSN EN 1990. Základní rovnice má obecný tvar:

E_d = γ_Sd (γ_g,j G_k,j + γ_q,1 Q_k,1 + γ_q,i ψ_0,i Q_k,i)

Význam symbolů:

E_d: výsledná hodnota zatížení
γ_Sd: součinitel modelové nejistoty; pro většinu případů pro uvážení pokládáme součinitel γ_Sd = 1
γ_g,j: dílčí součinitel (j-tého) stálého zatížení
G_k,j: charakteristická hodnota (j-tého) stálého zatížení
γ_q,1: dílčí součinitel (prvního) proměnného zatížení
Q_k,1: charakteristická hodnota (prvního) proměnného zatížení
γ_q,i: dílčí součinitel (i-tého) stálého zatížení
ψ_0,i: součinitel pro kombinační hodnotu (i-tého) proměnného zatížení
Q_k,i: charakteristická hodnota (i-tého) stálého zatížení

Norma uvádí tři možnosti kombinační rovnice s různě nastavenými součiniteli zatížení. Pro výpočet můžeme volit první rovnici nebo jednu z dalších dvou, tu s nejnepříznivějšími účinky.

Návrhové hodnoty zatížení ( STR/GEO) podle ČSN EN 1990

Tab. 1 – Návrhové hodnoty zatížení (STR/GEO) podle ČSN EN 1990
Výraz	Stálé nepříznivé	Stálé příznivé	Proměnné hlavní	Proměnné vedlejší nejúčinnější	Proměnné vedlejší ostatní
6.10	1,35 ‧ `G`_k,j,sup	1,0 ‧ `G`_k,j,inf	1,5 ‧ `Q_k,j`	–	1,5 ‧ `ψ`_0,i ‧ `Q_k,i`
6.10a	1,35 ‧ `G`_k,j,sup	1,0 ‧ `G`_k,j,inf	–	1,5 ‧ `ψ`_0,1 ‧ `Q_k,i`	1,5 ‧ `ψ`_0,i ‧ `Q_k,i`
6.10b	1,35 ‧ 0,85 ‧ `G`_k,j,sup = 1,15 ‧ `G`_k,j,sup	1,0 ‧ `G`_k,j,inf	1,5 ‧ `Q_k,j`	–	1,5 ‧ `ψ`_0,i ‧ `Q_k,i`

3. Srovnání na referenční budově

Pro porovnání účinků byla vybrána referenční budova o výšce 6 podlaží, což v daných podmínkách českých měst odpovídá nejvyšší obvyklé zástavbě a časté nejvyšší možné zástavbě povolené v daném území a územními plány.

Referenční budova má 6 nadzemních podlaží, je řešena jako trojtrakt a základní modul nosných konstrukcí krajních traktů je 6 × 6 metrů. Střední trakt je zúžen na 1,5 metru pro chodbu. To odpovídá častému řešení u stěnových konstrukcí.

Budova je uvažována jako obytná, tzn. s užitným zatížením na podlaze kategorie A – obytné plochy a plochy pro domácí činnosti. Zde je obvyklá hodnota rovnoměrného užitného zatížení 1,5 kN/m². Bylo provedeno modelování pro jiné světlosti traktů a i pro vyšší hodnotu rovnoměrného užitného zatížení, a to do kategorie C1 – plochy pro shromažďování osob, konkrétně školy s hodnotou užitného zatížení 3,0 kN/m² a zároveň vyhovující pro kancelářské plochy kategorie B s hodnotou užitného zatížení 2,5 kN/m².

Výsledky porovnávají různý postup při sestavení síly v bodech sloupů modulu 6 × 6 metrů, pro vnější i vnitřní podporu. Dokumentují síly na úrovni pod stropem prvního podlaží pro návrh dřevěného sloupu od účinků svislého zatížení. Pro porovnání jsou uvedeny síly v daném místě při použití železobetonového montovaného skeletu a při úpravě na zděný stěnový systém, který je často používanou konstrukcí bytových domů. Zde se v místě dřevěného sloupu předpokládá zděný pilíř jako část obvodové nebo vnitřní nosné stěny.

Výsledky jsou patrné z tabulek pro obvodový a střední nosný prvek (sloup, pilíř). K výpočtům byl použit program autora příspěvku.

Tab. 2 – Porovnání velikosti svislé síly u obvodového nosného prvku
šestipodlažní budovy na úrovni pod stropem 2. podlaží
	Provedení	Kombinace zatížení [kN]
	Provedení	kvazistálá	častá	charakt.	6.10.	6.10a	6.10b	6.10b/6.10
1	skládaný strop a stěny z cihel	0	0	0	1255	1222	1097	0,87
2	montovaný žb.skelet				1172
3	dřevěný skelet a stěny	356	383	438	610	585	549	0,90
	poměr 2 ku 3				0,52
	poměr 1 ku 3				0,49	0,48	0,50

Tab. 3 – Porovnání velikosti svislé síly u vnitřního nosného prvku
šestipodlažní budovy na úrovni pod stropem 2. podlaží
	Provedení	Kombinace zatížení [kN]
	Provedení	kvazistálá	častá	charakt.	6.10.	6.10a	6.10b	6.10b/6.10
1	skládaný strop a stěny z cihel	0	0	0	1448	1408	1313	0,91
2	montovaný žb.skelet				1440
3	dřevěný skelet a stěny	356	457	524	730	699	671	0,92
	poměr 2 ku 3				0,50
	poměr 1 ku 3				0,50	0,50	0,51

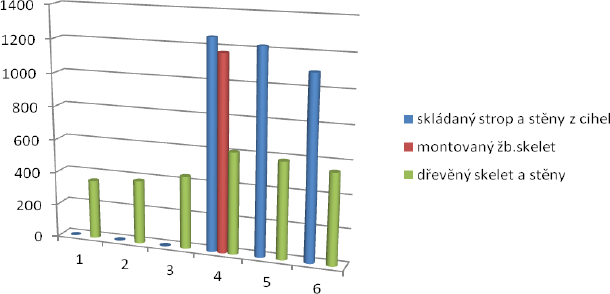
Graf 1 – Výsledky porovnání účinků zatížení na nosný prvek 1. podlaží, síly jsou v kN

Popis:
1 – kvazistálé zatížení
2 – častá kombinace zatížení
3 – charakteristické kombinace
4 – návrhová mezní kombinace zatížení podle rovnice 6.10
5 – návrhová kombinace podle rovnice 6.10a
6 – návrhová kombinace podle rovnice 6.10b

V příspěvku je uveden pouze výběr – část z provedených modelů a výpočtů dřevných konstrukcí variant referenční budovy.

Pro danou referenční budovu představuje skutečné téměř trvalé zatížení dané kvazistálou kombinací zatížení 64,8 % návrhové hodnoty zatížení na svislé konstrukce a pro častou kombinaci činí podíl 69,7 %, a to vůči postupu z rovnice 6.10b.

4. Závěr

Z provedené analýzy byly sestaveny následující závěry a doporučení:

4.1 Výpočet svislé síly

Pro kombinaci návrhového mezního zatížení sestavnou pro svislé síly na sloupy a pilíře ev. stěny vnějších i vnitřních stěn doporučuji použít vhodný postup s příznivým ekonomickým a technickým dopadem na návrh svislého prvku. Konkrétně jde použití rovnice 6.10b podle ČSN EN 1990. Úspora se pohybuje kolem 8 až 10 %, přesněji je stanovena ve výpočtech.

4.2 Provozní zatížení

Z provedených výpočtů vyplývá, že vybrané budovy je hodnota provozního zatížení přibližně pod 70 % návrhové hodnoty mezního zatížení svislé konstrukce stanovené podle doporučeného postupu. Při porovnání s mezní hodnotou (podle rovnice 6.10) bude rozdíl ještě vyšší (63 %). Je tudíž k diskuzi, jak je uvedený postup podle eurokódu konzervativní.

4.3 Nižší síla na základy

Užití dřevěných nosných konstrukcí pro šestipodlažní budovu dává více jak poloviční zatížení na základy při porovnání s budovou zděnou nebo s konstrukcí ze železobetonového skeletu. Tento výsledek lze očekávat u podobných dřevěných vysokých staveb. Pro zatížení základů (mezní stav GEO) platí i zjištění uvedená v bodě 4.2.

4.4 Účinky větru

Při návrhu nosného systému a základů nutno mimo svislé síly uvažovat s účinky větru na budovu. Konstrukci je třeba navrhnout s diagonálním ztužením ve dvou svislých směrech s pokud možno symetrickým rozdělení v půdorysu stavby. Dalším řešením je vložení ztužujících stěn nebo monolitického jádra.

4.5 Doporučení k podrobnosti výpočtu dřevěných konstrukcí

Pro návrhy a výpočty na úrovni prvotních návrhů konstrukcí a dokumentace po stavební povolení doporučuji provést volbu mezi konzervativnější metodou s rovnicí 6.10 a rovnicemi 6.10a a 6.10b. Použití rovnice 6.10 s vyššími výsledky v prvotnější fázi návrhu konstrukce může pokrýt i doplňky a změny, které mohou přijít v dalším stupni dokumentace. Pro definitivní návrhy a prováděcí a výrobní dokumentaci navrhuji užívat rovnici 6.10b s příznivějšími výsledky výpočtu zatížení včetně nižších účinků na základy.

Literatura a podklady

Normy zmíněné v textu – ČSN EN 1990, 1991-1-1 a původní ČSN 73 00 35

English Synopsis

Determination of vertical forces from load of a wooden high-rise building

The magnitude of the load on the walls of tall wooden constructions can be assembled according to the existing standards according to the valid combination equations in several ways. There are differences between the results. Determining the appropriate procedure for determining vertical strength from construction in different parts of building preparation and comparing it with other options is the subject of this paper.