Stabilita jednostranně opláštěných stěnových panelů pro dřevostavby
V současné době se navrhování stěnových panelů s výztuhami s průřezem ve tvaru I a oboustranným opláštěním provádí na základě výsledků zkoušek a zjednodušeného analytického výpočtu. V případě jednostranně opláštěných panelů ale nejsou mechanismy chování ani způsob porušení stále dostatečně prozkoumány. Hlavním cílem článku je proto popsat chování výše zmíněného systému, vytvořit spolehlivý model a zpracovat parametrickou studii s využitím experimentální a numerické analýzy. Výsledky práce bude možné využít pro efektivnější využití subtilních sloupkových systémů dřevostaveb.
Úvod
S nástupem moderních technologií v oblasti opracovávání dřeva je možné v lehkém skeletu dřevostaveb kromě klasických průřezů využít i prvky složené z různých materiálů a z několika částí. Jedná se o dřevěný lepený kompozitní prvek s průřezem ve tvaru I tvořený stojinou z desky na bázi dřeva zapuštěné do pásnic z rostlého nebo lepeného lamelového dřeva. Použití těchto prvků jako výztužných žeber ve stěnových a stropních panelech má oproti klasickým sloupkům a nosníkům obdélníkového tvaru hned několik výhod: úsporu materiálu, vysokou únosnost, nižší hmotnost umožňující snadnější manipulaci, jednodušší realizaci otvorů pro instalace, eliminaci tepelných mostů ve skladbě konstrukce a také výbornou tvarovou a rozměrovou stabilitu.
![Obr. 1a: Prvky s průřezem ve tvaru I podle [1]. Fig. 1a: Elements with I-shaped cross section by [1]](/docu/clanky/0184/018479o1.jpg)
Obr. 1: Prvky s průřezem ve tvaru I (vlevo) podle [1], redukce tepelného mostu (vpravo)
Fig. 1: Elements with I-shaped cross section (on the left) by [1], reduction of thermal bridge (on the right)
Na obr. 1 jsou vidět prvky s průřezem ve tvaru I s různými výškami průřezu a je znázorněno omezení tepelného mostu v místě I-sloupku.
Cíle výzkumu
V současné době se navrhování stěnových panelů s výztuhami s průřezem ve tvaru I a oboustranným opláštěním provádí na základě výsledků zkoušek a zjednodušeného analytického výpočtu. V případě jednostranně opláštěných panelů ale nejsou mechanismus chování ani způsob porušení stále dostatečně prozkoumány. Hlavním cílem této práce je proto popsat chování výše zmíněného systému, vytvořit spolehlivý model a zpracovat parametrickou studii s využitím experimentální a numerické analýzy. Předpokládá se, že výsledky práce bude možné využít pro efektivnější využití subtilních sloupkových systémů dřevostaveb. Výstupem práce bude návrhový model a dimenzační tabulky pro jednostranně opláštěné sloupkové systémy s výztužným žebrem tvořeným I-sloupkem.
Experimenty
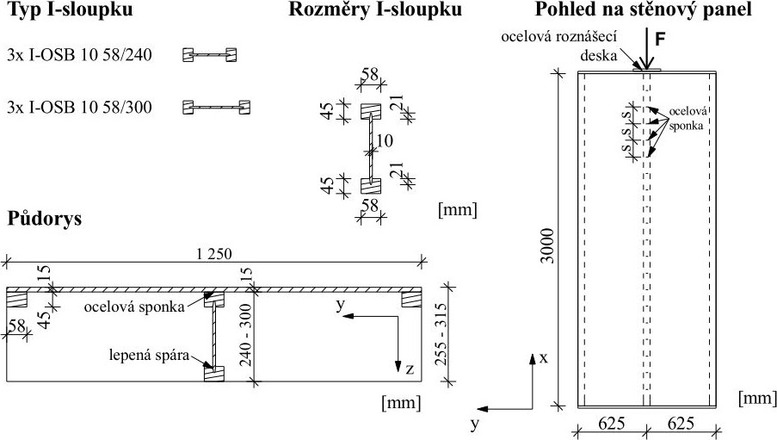
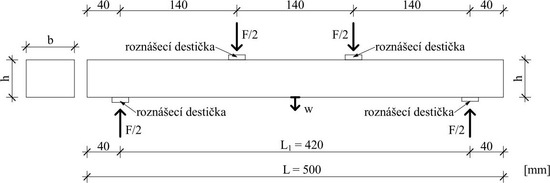
V rámci experimentální části práce byly navrženy a provedeny statické zkoušky na stěnových panelech reálných rozměrů s výztuhou tvořenou dřevěným lepeným kompozitním prvkem s průřezem ve tvaru I a jednostranným opláštěním. Uspořádání experimentu a rozměry jednotlivých komponent i celého vzorku jsou znázorněny na obr. 2.
Obr. 2: Uspořádání zkoušky stěnového panelu
Fig. 2: Test set up of wall panel
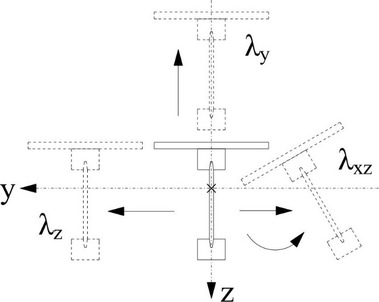
Před návrhem statických zatěžovacích zkoušek byl proveden analytický výpočet pro několik způsobů možného vybočení průřezu stěnového panelu dle [2] a [3], obr. 3 a byl vytvořen prostorový numerický model pro předpověď chování, únosnosti a způsobu porušení stěnového panelu.
Při výběru rozměrů nosného I-sloupku stěnového panelu bylo mimo jiné také přihlédnuto k aktuálním požadavkům na tepelně technické vlastnosti obvodových stěn, především na dosažení hodnot součinitele prostupu tepla U [W/m2K] celé stěny odpovídající normovým hodnotám pro nízkoenergetické a pasivní domy dle [4]. Jelikož nosný I-sloupek tvoří celistvý prvek, vznikají v konstrukci systémové tepelné mosty. Přerušení těchto tepelných mostů se v současné době nejčastěji provádí aplikací vnějšího zateplovacího systému. Na základě vypočtených hodnot součinitele prostupu tepla byly zvoleny I-sloupky s výškou průřezu 240 mm a 300 mm.
Obr. 3: Způsob vybočení průřezu stěnového panelu při analytickém výpočtu (vlevo), deskostěnový model pro numerickou analýzu (vpravo)
Fig. 3: Buckling modes for analytical calculation (on the left), 2D-elements model for numerical calculation (on the right)
Připravený stěnový panel byl postaven do prostoru zkušební brány pod zatěžovací válec se siloměrem, který bude zatěžovat stěnový panel přes ocelovou roznášecí desku. Pro dosažení co nejreálnějších podmínek během zkoušky byl stěnový panel na krajích stabilizován proti posunu pomocí upínacích textilních popruhů, obr. 4.
Obr. 4: Stěnový panel umístěný pod zatěžovacím válcem: způsob uchycení (vlevo), deformovaná konstrukce (vpravo)
Fig. 4: Wall panel placed to the test area: type of anchoring (on the left), deformed structure (on the right)
Před provedením experimentu byly změřeny imperfekce volné pásnice. Na základě imperfekcí byl odhadnut směr vybočení volné pásnice.
Na konstrukci byly osazeny potenciometrické snímače dráhy, které měřily vodorovné posuny na volné pásnici I-sloupku v rovině stěny v pěti bodech po výšce I-sloupku a vodorovné posuny hranolů na krajích OSB desky z roviny stěny ve třech bodech po výšce hranolů.
Zatěžování stěnového panelu bylo řízeno deformací, neboli posunem zatěžovacího válce rychlostí 2 mm/min. Při průběhu experimentu se stěnový panel deformoval dle předpokladů numerického 3D modelu. I-sloupky během experimentu vždy vybočily ve směru naměřené imperfekce.
Obr. 5: Závislost síla-deformace
Fig. 5: Load-deflection curve
Opláštění z OSB desky bylo k pásnici I-sloupku připojeno sponkami v roztečích 100, 150 a 200 mm. Při postupném zatěžování stěnového panelu se zpočátku vždy začal mírně natáčet I-sloupek, z držené pásnice se začaly vytahovat sponky a začala vznikat mezera mezi opláštěním a připojenou pásnicí. Volná pásnice začala v oblasti poloviny výšky mírně vybočovat v rovině stěnového panelu.
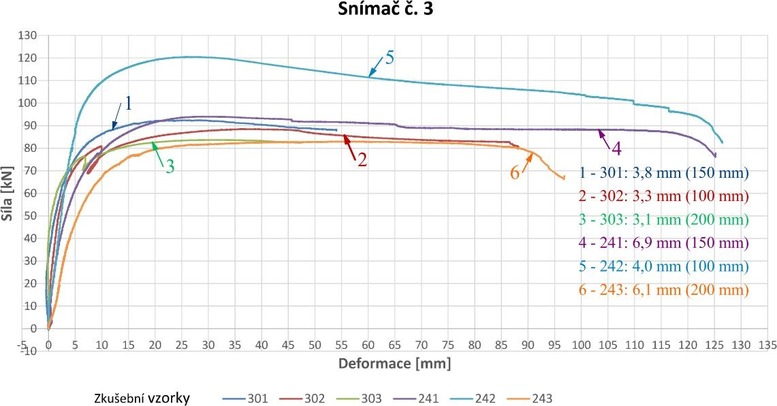
Kolaps konstrukce a pokles působící síly byly v případě velkých roztečí sponek zpravidla způsobeny vytažením a protažením ocelových sponek a I-sloupek vybočil v rovině stěny. V případě menších roztečí sponek sponky drženou pásnici udržely a kolaps konstrukce byl způsoben porušením a vybočením volné pásnice v rovině stěnového panelu. Maximální síla u I-sloupku s výškou průřezu 300 mm byla dosažena v rozmezí 330 až 400 vteřin, u I-sloupku s výškou průřezu 240 mm v rozmezí 410 až 465 vteřin. Závislost působící síly na vodorovném posunu volné pásnice v polovině výšky I-sloupku (snímač č. 3) je na obr. 5.
Průběh křivek je závislý na počátečních imperfekcích, ale také na rozteči sponek, které spojují opláštění z OSB desky s pásnicí I-sloupku. V pravé části obr. 5 jsou uvedeny naměřené počáteční imperfekce a vzdálenosti sponek u jednotlivých vzorků.
Materiálové zkoušky
V průběhu zkoušek vzpěrné únosnosti stěnových panelů byla zjištěna vlhkost dřeva pomocí elektrického odporového vlhkoměru T510 se zarážecí elektrodou TS 070, (obr. 6 vlevo), na několika místech stěnového panelu. Průměrná hodnota vlhkosti byla 7,4 %.
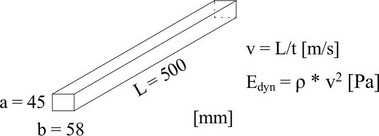
Obr. 6: Elektrický odporový vlhkoměr (vlevo), přístroj Fakopp (uprostřed nahoře), přístroj Sylvatest (vpravo nahoře), vzorky pro materiálové zkoušky (uprostřed dole), výpočet dynamického modulu pružnosti (vpravo dole)
Fig. 6: Absolute moisture meter (on the left), Fakopp device (in the middle top), Sylvatest device (on the right top), specimens for material tests (in the middle bottom), calculation of the dynamic modulus of elasticity (on the right bottom)
Po provedení zkoušek byly části stěnových panelů rozřezány na menší vzorky pro určení mechanických vlastností dřeva a OSB desek, (obr. 6 dole). Vzorky byly přeměřeny, zváženy a následně byla stanovena jejich hustota ρ. Průměrná hodnota hustoty dřeva je 425 kg/m3 a průměrná hodnota hustoty OSB desky je 610 kg/m3.
U dřeva byl zjišťován modul pružnosti pomocí dynamických zkoušek metodou rázové vlny pomocí přístroje Fakopp a ultrazvukovou metodou pomocí přístroje Sylvatest, (obr. 6 uprostřed nahoře a vpravo nahoře). Výsledkem měření byl čas průchodu akustického signálu t (rázové a ultrazvukové vlny) dřevěným vzorkem. Z tohoto času byla určena rychlost průchodu vlny v a následně dynamický modul pružnosti Edyn, Obr. 6 vpravo dole. Průměrná hodnota dynamického modulu pružnosti z přístroje Fakopp je 15817 MPa a z přístroje Sylvatest 14135 MPa. Měření oběma metodami probíhalo mezi čely jednotlivých vzorků.
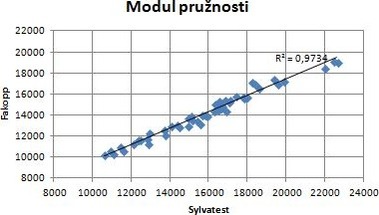
Obr. 7: Porovnání výsledků dynamických modulů pružnosti
Fig. 7: Comparison of the results of dynamic modulus of elasticity
Porovnání výsledků pro metodu rázové vlny a ultrazvukovou metodu je znázorněno na obr. 7. Koeficient korelace R mezi těmito metodami vychází 0,987. Mírou korelace mezi dynamickým modulem pružnosti měřeného přístroji Fakopp a Sylvatest se zabýval ve své práci také například Pošta [5]. Došel k hodnotě R = 0,94, při které přikládal sondy obou přístrojů na horní povrch pod úhlem 45°. Lze tedy říci, že měřením při kterém se sondy přiloží na čela jednotlivých vzorků je dosaženo minimálně stejné nebo i vyšší míry korelace než u sond přiložených na povrch vzorku.
Na stejných vzorcích byl modul pružnosti zjišťován také statickými destruktivními zkouškami pomocí čtyřbodové ohybové zkoušky na zatěžovacím stroji MTS, schéma zkoušky je znázorněno na obr. 8. Průměrná hodnota statického modulu pružnosti je 10635 MPa.
Obr. 8: Schéma čtyřbodové zatěžovací zkoušky
Fig. 8: Schema of a four-point bending test
Pro vyhodnocení přesnosti jednotlivých metod pro zjištění modulu pružnosti je určena korelace mezi moduly pružnosti zjištěnými z dynamických a statických zkoušek. Z výsledků je patrná dobrá korelace mezi metodami. Koeficienty korelace jsou sepsány v tab. 1.
| Koeficient korelace | Dynamický modul pružnosti | ||
|---|---|---|---|
| EDYN,F | EDYN,S | ||
| Statický modul pružnosti | ESTAT,C | 0,90 | 0,91 |
Získané koeficienty korelace lze porovnat s údaji z obdobných měření od jiných autorů: Pošta [5] došel ke korelaci 0,80 a např. Dolejš [6] došel ke korelaci 0,87.
Ze stejné zkoušky, která byla provedena pro zjištění statického modulu pružnosti, se získá také pevnost v ohybu fm: zde s průměrnou hodnotou 50,2 MPa. Obdobným způsobem byly zjištěny mechanické vlastnosti pro OSB desky: průměrná hodnota modulu pružnosti ve směru vláken je 8280 MPa a kolmo na vlákna 2596 MPa, průměrná hodnota pevnosti v ohybu ve směru vláken je 26,5 MPa a kolmo na vlákna 12,6 MPa.
Dále byly provedeny zkoušky pro zjištění únosnosti ocelových sponek. Byl použit typ ocelové sponky stejného typu, který byl použit při experimentech na stěnových panelech reálných rozměrů. Pro sestavení vzorků byly použity dřevěné hranoly a OSB deska vyříznuté ze zkušebních vzorků stěnových panelů. Byly sestaveny vzorky a provedena zkouška v tlaku pro zjištění únosnosti ocelových sponek ve střihu. Vzorky, umístění ve zkušebním stroji a deformovaný vzorek jsou vidět na obr. 9.
Obr. 9: Vzorky pro zkoušku sponkového spoje (vlevo), umístění v zatěžovacím stroji (uprostřed), deformovaný vzorek (vpravo)
Fig. 9: The samples for test (on the left), placement in the MTS loader (in the middle) deformed sample (on the right)
Zjištěné mechanické vlastnosti dřeva a OSB desky a hodnoty únosnosti sponkového spoje budou použity pro validaci numerického modelu.
Závěr
Po provedení série zkušebních vzorků pro stanovení vzpěrné únosnosti panelů se ukázala dobrá shoda mezi experimentem a numerickým modelem. Stěnový panel se porušil předpokládaným způsobem. Maximální síla působící na stěnový panel zjištěná při experimentu byla v průměru o cca 40 % vyšší než předpokládaná únosnost vypočtená podle předběžného analytického výpočtu. Na základě výsledků zkoušek lze také konstatovat, že I-sloupek s výškou průřezu 240 mm má vyšší únosnost než I-sloupek s výškou průřezu 300 mm, který je již více náchylný na ztrátu stability vybočením volné pásnice.
Literatura
- http://www.archiexpo.com/prod/metsaewood/product-60821-147364.html – online, viděno 5. června 2015
- ČSN EN 1995-1-1: (73 1701) Eurokód 5: Navrhování dřevěných konstrukcí – Část 1-1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby. ČNI, prosinec 2006
- ČSN EN 1999-1-1: (73 1501) Eurokód 9: Navrhování hliníkových konstrukcí – Část 1-1: Obecná pravidla pro konstrukce. Praha: ČNI, únor 2009
- ČSN 73 0540-2: Tepelná ochrana budov – Část 2: Požadavky. Praha: Centrum technické normalizace na Fakultě stavební ČVUT v Praze, říjen 2011
- POŠTA, Jan. Využití radiometrie při nedestruktivním zkoušení dřevěných prvků in-situ. Praha: ČVUT 2015. Disertační práce. České vysoké učení technické v Praze, Fakulta stavební, Katedra ocelových a dřevěných konstrukcí.
- DOLEJŠ, Jakub. Využití nedestruktivních metod k vyšetřování mechanických vlastností dřeva. Praha: ČVUT 1997. Disertační práce. České vysoké učení technické v Praze, Fakulta stavební, Katedra ocelových a dřevěných konstrukcí.
The subject of this paper is an experimental and numerical analysis of the stability of the wall panels with one-side board sheating. The reinforcement of the panel is provided by means of glued timber composite I-shaped element consisting of a web made of a wood-based desk embedded into flanges of solid timber. The mechanism of the behaviour of these panels, mode of the failure and reliable procedure to determine the buckling load-bearing capacity not been fully explored so far. The main aim of this project is to create reliable numerical model using experiments and parametric study for optimized design. Outcome of the work is a design model and dimension tables for one-side board sheating wall panels of light timber structures with a rib in the form of an I-stud.
