Dřevobetonový strop vystavený požáru
Předmětem tohoto příspěvku je numerická analýza chování dřevobetonové kompozitní stropní konstrukce, tvořené vláknobetonovou deskou a dřevěnými nosníky z lepeného lamelového dřeva. Hlavním cílem je posoudit možnost využití vláknobetonové desky, která spolupůsobí s dřevěnými nosníky a pomocí modelů v programu Ansys vyšetřit její chování v zatížené stropní konstrukci. Přesnost numerické analýzy dřevobetonových konstrukcí plně závisí na použitých materiálových modelech, proto jsou provedené materiálové modely ověřeny na základě experimentálních výsledků.
Úvod
Analýza skutečného chování konstrukčního prvku nebo konstrukčního systému může být provedena buď pomocí experimentů, nebo za použití numerického modelování. Mnohdy nákladné experimenty mohou z části nahradit numerické modely, avšak nutnou podmínkou je zavedení přesných materiálových modelů, které s dostatečnou přesností aproximují reálné vlastnosti a dále zavedení jen nejnutnějších zjednodušujících předpokladů, které nebudou mít vliv na výsledky numerických simulací a jejich shodu s reálným chováním konstrukce. Vždy je však třeba verifikovat výsledky numerické analýzy s experimentem, nebo naopak kalibrovat parametry numerického modelu podle provedených experimentů. Numerické modely tak lze výhodně využít k pravděpodobnostním a spolehlivostním.
Zkouška stropní konstrukce
V rámci experimentálního programu byla vyrobena dřevobetonová deska o rozměru 3,0 × 4,5 m pro zkoušku za zvýšené teploty. Deska o tloušťce 60 mm byla vybetonována na dřevěný rám z lepeného lamelového dřeva GL24h průřezu 200/240 mm s dvěma dřevěnými stropnicemi průřezu 120/160 mm. Beton byl vyztužen 70 kg/m3 drátky typu HE 75/50 Arcelor, pevnosti 1200 MPa a dosáhl při materiálových zkouškách za běžné teploty pevnosti v tlaku 52,3 MPa a pevnosti v příčném tahu 5,8 MPa. Spřažení bylo zajištěno TCC šrouby průměru 7,3 mm a délky 150 mm ve dvou řadách pod úhlem 45° s roztečí 100 mm v podélném směru a 40 mm v příčném směru. Zkouška dřevobetonové stropní konstrukce proběhla v požární zkušebně PAVUS ve Veselí nad Lužnicí. Za zvýšené teploty bylo zatížení desky vyvozeno 2 břemeny o rozměrech 0,3 × 0,3 × 1,8 m a teplotou plynu podle nominální normové teplotní křivky. Zkušební vzorek byl navržen na požární odolnost R60.
Model stropní konstrukce
1. Diskretizace
Za účelem termo-mechanické analýzy konstrukce byl vytvořen 3D model pomocí metody konečných prvků, viz Obr. 1-1. Model dřevobetonové stropní konstrukce s rozptýlenou výztuží se skládá z vláknobetonové desky a dřevěných nosníků. Tyto části byly diskretizovány SOLID prvky s ohledem na skutečnou geometrii konstrukce. Diskretizace pomocí SOLID prvků byla vybrána kvůli lepšímu znázornění víceosého stavu napětí a přesné modelaci teplotního gradientu napříč tloušťce vláknobetonové desky.
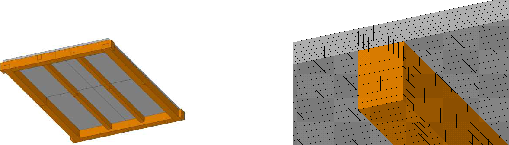
Obr. 1-1: Model spřažené dřevobetonové stropní konstrukce s rozptýlenou výztuží
Předkládané simulace jsou velmi časově náročné díky materiálovým a geometrickým nelinearitám způsobeným hlavně odhoříváním dřeva, teplotní degradací a změkčení SFRC. Proto byla na základě podmínek symetrie sestavena pouze část modelu a byly zkoušeny různé způsoby síťování, aby byla nalezena nejlepší kompromis mezi rychlostí a přesností. Konečný model se skládal ze 43 909 elementů a 53 360 bodů.
Pro numerickou analýzu stropní konstrukce bylo chování spřahovacích prvků z numerického modelu nahrazeno ideálně pružno-plastickým chováním ve smyku a v tahu.
2. Teplotní analýza
Přestup tepla v konstrukci byl uvažován jako transientní nelineární problém se zahrnutím integrace podle Newmarka, viz Eurokód 2-1-2. Jako okrajové podmínky byly na straně požáru uvažovány radiace a konvekce na základě teplot naměřených v peci a na odvrácené straně konstantní teplota 12 °C. Materiálové hodnoty pro beton a pro dřevo byly převzaty z Eurokódu 2-1-2 a Eurokódu 5-1-2. Výsledky těchto hodnot byly porovnány s výsledky podle Kodura (Kodur, 1998). Pro konvekci byl použit koeficient teplotní roztažnosti na straně požáru 35 W.m−2.K−1 a na odvrácené straně 30 W.m−2.K−1. Koeficient emisivity a radiace byl použit 0.9.
3. Vstupní data
1.1. Materiálový model pro dřevo
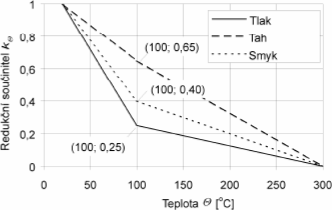
Pro simulaci chování dřevobetonového vzorku byl pro dřevěnou část použit isotropní materiál s plasticitou. Data byla převzata z ČSN EN 1194 pro lepené lamelové dřevo GL24h (modul pružnosti rovnoběžně s vlákny 11 600 MPa, modul pružnosti kolmo na vlákna 390 MPa, modul pružnosti ve smyku 720 MPa a pevnost v tahu rovnoběžně s vlákny 16.5 MPa). Zuhelnatění dřeva bylo uvažováno jako redukce modulu pružnosti a tahové pevnosti díky změnám teploty, viz Obr. 1-2. Křivky tohoto chování byly získány z Eurokódu 5. Je obtížné popsat přesně závislost anisotropického kritéria plasticity na teplotě, proto bylo použito isotropní kritérium plasticity, které omezuje pouze pevnost v tahu rovnoběžně s vlákny. Koeficient teplotní roztažnosti je menší než pro SFRC, proto nehraje tak důležitou roli. Teplotní závislost také není tak významná díky rychlé teplotní degradaci a zuhelnatění dřeva, proto byla použita pouze konstantní hodnota teplotní závislosti 4.5E-6 °C−1.
1.2. Materiálový model pro SFRC
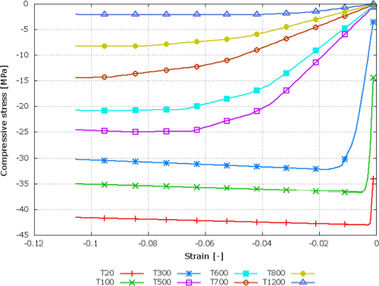
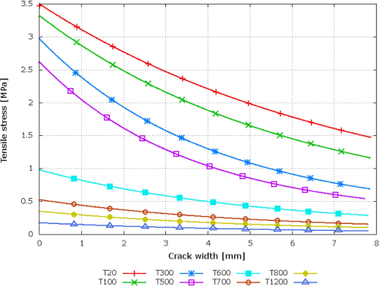
Pro kalibraci materiálových modelů byly provedeny laboratorní zkoušky za běžné a zvýšené teploty. Jako nejvhodnější pro modelaci SFRC za zvýšených teplot byl použit Microplane model dostupný v ANSYS FE-kódu. Tento model je vhodný pro modelování s poškozením díky rozsáhlému zatížení a teplotní degradaci. Vstupní data materiálového modelu pro Microplane model byly kalibrovány na měřeních získaných z čtyřbodových zkoušek za běžné teploty a zvýšené teploty a ze zkoušek vláknobetonových krychlí a trámců. Kalibrovaná křivka závislosti síly a napěti v tlaku a křivka tloušťky trhlin v tahu pro různé teploty jsou ukázány na Obr. 1-3.
Velmi důležitou roli v termo-mechanické analýze hraje teplotní roztažnost. Pro SFRC byla převzata teplotní roztažnost pro silikátové betony z Eurokódu 3.
1.3. Materiálový model spřažení
Pro kalibraci smykového spojení byl vytvořen model, kde jsou šrouby rozetřeny pomocí speciálního kontaktu, který může přenášet smykové zatížení s definovanou silou, jak ukazuje Obr. 1-4. Smyková síla musí být kalibrována na maximální zatížení díky selhání nebo zatlačení šroubů. Model byl zatěžován předepsaným posunem a měřila se síla. Materiálové vlastnosti obou modelů byly kalibrovány na změřené křivky závislosti síly na posunu. Výsledky získané z modelů byly porovnány s naměřenými, jak ukazuje Obr. 1-5. Představené numerické analýzy zlepšují použitelnost obou materiálů v mechanických simulacích stropní konstrukce vystavené požáru.
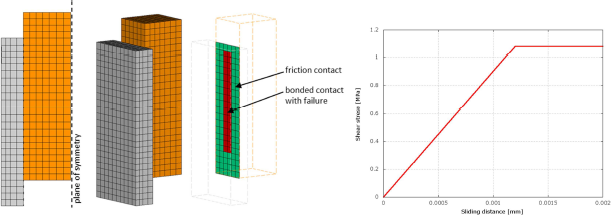
Obr. 1-4: Numerický model protlačovací zkoušky s rozetřeným modelování spřahovacích prvků (vlevo), graf závislosti síly a posunu pro rozetřené modelování spřahovacích prvjů (vpravo)
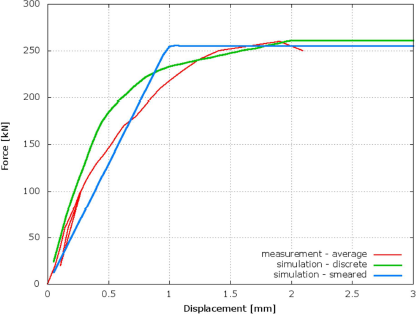
Obr. 1-5: Numerický model dřevobetonového vzorku a experimentálně získaná křivka závislosti síly na posunu pro první sérii ST-1
Závěr
Výstupem řešení je ověřený numerický model stropní konstrukce, který lze dále modifikovat pro další experimenty podobného typu a pro určení požární odolnosti zkoušených typů dřevobetonových stropních konstrukcí.
Poděkování
Příspěvek vznikl za podpory projektu Grantové agentury České republiky č. P105/10/2159 a za podpory Evropské unie, projektu OP VaVpI č. CZ.1.05/2.1.00/03.0091 – Univerzitní centrum energeticky efektivních budov.
Literatura
- [1] Kuklíková, A. 2004. Kompozitní dřevobetonové konstrukce. ČVUT v Praze, Disertační práce. Praha.
- [2] Petřík, V., Philipp, N., Křístek, V., Půlpán, M. 2011. Full-scale testy kompozitních konstrukcí FRC-dřevo a UHPFRC-dřevo. 18. konference Betonářské dny, Sekce: Mosty 2: 337–342. Praha.
- [3] Kodur, V. K. R & Lie, T. T. 1996 Thermal and mechanical properties of steel-fibrereinforced concrete at elevated temperatures. Can. J. Civ. Eng. 23: 511–517.
- [4] Dias, A. M. P. G., Van de Kuilen, J. W., Lopes, S., Cruz, H., 2007. A non-linear 3D FEM model to simulate timber-concrete joints. Advances in Engineering Software 38:522–530.
- [5] Šlapka, P. 2011. Numerická simulace chování spřažených dřevovláknobetonových konstrukčních prvků. ČVUT v Praze, Diploma thesis. Praha.
- [6] Holschmacher, K., Klotz, S., Weise, D. 2002. Application of steel fibre reinforced concrete for timber-concrete composite constructions. Lacer No. 7.2002: 161–170.
This paper presents a numerical analysis of the mechanical behaviour of timber-concrete composite floors in fire, which consists of steel fibre reinforced concrete board and glue-laminated timber beams. The main aim of this model is to assess the using of steel fibre reinforced concrete board, which work together with glue-laminated timber beams and due to the models in Ansys programme investigate its behaviour in loaded construction. Accuracy of numerical analysis of this structure fully depends on material models used in the analysis. Therefore the implemented material models must be verified on the basis of experimental results. All this modeling was done using a commercial programme Ansys 14.