Rozšířená metoda pro řešení 3D oblastí diskontinuit v oblasti betonových konstrukcí

1. Úvod

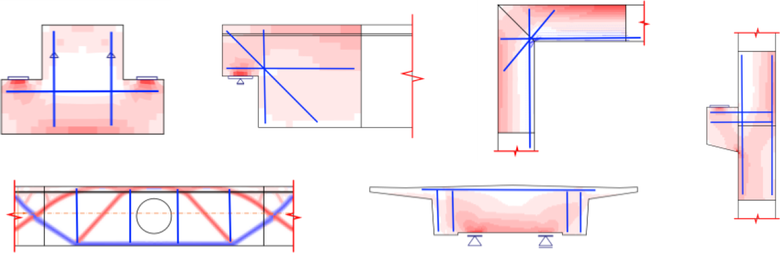
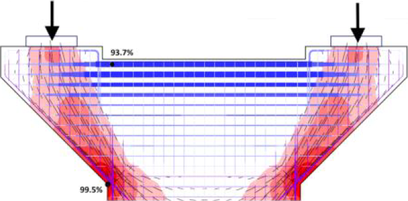
Většina stavebních inženýrů, zabývajících se betonovými konstrukcemi, se během své projekční praxe setká s návrhem oblastí diskontinuit (D-oblastí), viz Obr. 1, tedy oblastí, kde neplatí Bernoulli-Navierova hypotéza o zachování rovinnosti průřezu. Jedná se o oblasti, ve kterých působí soustředěné zatížení, dochází k náhlé změně průřezu, rámové rohy, krátké konzoly apod. V mostním stavitelství jsou to pak např. hlavy pilířů, nadpodporové příčníky, deviátory atd. Při návrhu má inženýr několik možností, jak tyto oblasti posoudit a navrhnout jejich dostatečné vyztužení. Jedním ze způsobu je řešení pomocí příhradové analogie (dále SaT), která je uvedena v aktuálně platných návrhových normách. Použití metody SaT však vyžaduje poměrně značné zkušenosti s tvorbou správného příhradového modelu. Dalším způsobem může být použití softwaru určeného pro řešení 2D/3D prostorových úloh, který usnadňuje návrh a pomáhá pochopit chování konstrukce v nespojitých oblastech.

Obr. 1: Příklady oblastí diskontinuit

Jednou z takových aplikací je Detail společnosti IDEA StatiCa, jejíž výpočet rovinných úloh je založen na metodě kompatibilních polí napjatosti (CSFM), která byl vyvinuta ve spolupráci s univerzitou ETH v Zurichu a která je nyní nově rozšířena do třetí dimenze pro postihnutí prostorového chování konstrukce. Nespornou výhodou této metody oproti obecné metodě konečných prvků je zapracování normových předpokladů a požadavků a přímé posouzení nejen D-oblastí.

2. Compatible stress field method (CSFM)

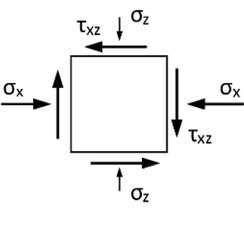
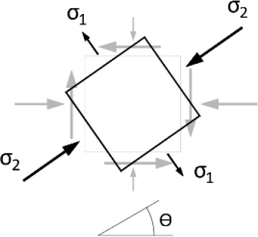
Princip CSFM lze vysvětlit na napjatosti základního rovinného elementu železobetonové konstrukce. Na obr. 2a je napjatost elementu, jak ji známe ze všech učebnic pružnosti a pevnosti, získaná například lineární, pružnou analýzou pomocí metody konečných prvků (MKP). Na element působí horizontální příčný tlak σ_x , vertikální příčný tlak σ_z a smykové napětí τ_xz . Z těchto napětí lze stanovit tzv. hlavní napětí a jejich sklon θ (Obr. 2b). Element je pak namáhán hlavním tahovým napětím σ₁ a hlavním tlakovým napětím σ₂, smykové napětí je nulové.

a)

b)

c)

Obr. 2: Princip CSFM: a) lineární, pružné napětí rovinného elementu; b) hlavní napětí; c) napětí při řešení pomocí CSFM

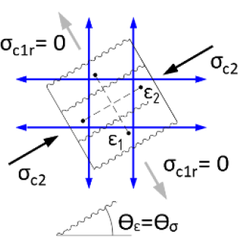
Na obr. 2c je pak zobrazena napjatost stejného elementu analyzovaného pomocí CSFM. Ve směru hlavních tlakových napětí σ₂ působí tlačený beton a vznikne tlakové pole s napětím σ_c2. V případě tahových napětí se vychází ze základního a bezpečného předpokladu norem, že beton v tahu nepůsobí, proto příčná hlavní tahová napětí σ₁ beton nepřenese a kolmo na jejich směr vznikne trhlina. Pro přenos tahových napětí tedy musí být součástí modelu výztuž, která veškeré tahy přenese (naznačena modře na obr. 2c).

Analýza pomocí CSFM je založena na metodě konečných prvků. Beton je modelovaný pomocí 2D stěnového elementu a výztuž pomocí 1D prutových prvků. Analýza se neprovádí v jednom kroku, jedná se o nelineární úlohu. Zatížení se během výpočtu aplikuje po přírůstcích a řešení nelineárního systému rovnic se hledá pomocí Newton-Raphsonovy metody. Fiktivní rozetřené trhliny (ε₁ je průměrná hodnota) se „tvoří“ kolmo na směr hlavních tlaků, který se může během nelineárního výpočtu měnit, jak se element od jednotlivých přírůstků zatížení „postupně potrhává“.

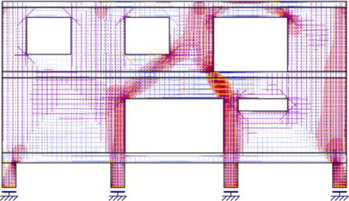
Provede-li se tato analýza napjatosti pomocí CSFM spojitě po celé řešené 2D oblasti, je výsledkem spojité tlakové pole a tlaková a tahová napětí ve výztuži. Zjednodušená grafická reprezentace CSFM napěťového pole např. pro stěnu s otvory nebo zhlaví pilíře je uvedena na Obr. 3.

CSFM používá běžné materiálové modely pro jednoosou napjatost (pracovní diagramy), které jsou definované v návrhových normách. Zohledňuje v nich jak tlakové změkčení betonu porušeného trhlinami od příčného tahu (tzv. compression softening), tak účinek taženého betonu mezi trhlinami na velikost napětí ve výztuži (tension stiffening).

Pro posouzení mezních stavů únosnosti se používá standardní normový formát spolehlivosti – metoda dílčích součinitelů spolehlivosti. A nespornou výhodou analýzy pomocí CSFM je rovněž schopnost posoudit mezní stavy použitelnosti: průhyby, omezení napětí a zejména šířku trhlin.

a)

b)

Obr. 3: Vykreslení napěťového pole: a) zhlaví pilíře; b) stěna s otvory

3. Rozšíření do třetí dimenze – 3D CSFM

3.1 Hlavní princip a základní předpoklady

V předchozí kapitole byl pro úplnost představen princip běžně používané metody CSFM. Cílem příspěvku je však představit její rozšíření do třetí dimenze – 3D CSFM, která již pracuje s trojosou napjatostí v betonu.

Metoda nadále bere v úvahu hlavní napětí v tlaku v betonu a napětí ve výztuži v místě trhliny; zanedbává přitom tahovou pevnost betonu, s výjimkou jejího ztužujícího účinku na výztuž (tahové ztužení je zahrnuto v pracovním diagramu výztuže). Z toho důvodu je důležité říci, že uvedená metoda není vhodná pro analýzu prostého nebo slabě vyztuženého betonu. A to právě z důvodu vyloučení betonu v tahu a kvůli tomu vznikajících trhlin, které musí být zachyceny výztuží. Chybějící výztuž může vést k zavádějícím deformacím a divergenci modelu.

a)

b)

c)

d)

e)

f)

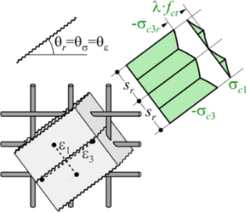
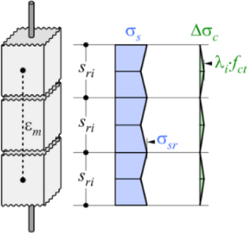
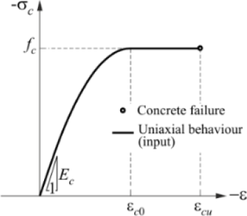
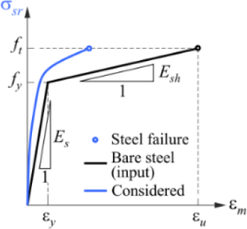
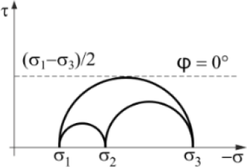
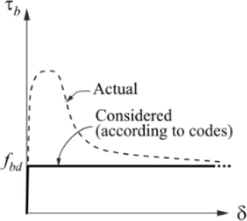
Obr. 4: Základní předpoklady 3D CSFM: a) hlavní napětí v betonu, b) napětí ve směrech výztuže, c) pracovní diagram betonu ve smyslu maximálních napětí, d) pracovní diagram výztuže ve smyslu napětí v trhlinách a průměrných poměrných přetvoření, e) Mohrovy kružnice pro beton, f) vztah napětí v soudržnosti a pokluzu pro posudky kotevních délek

Na rozdíl od 2D CSFM, kde pro materiálový model betonu stačí standardní jednoosý parabolicko-rektangulární pracovní diagram, tak u prostorové úlohy je nutno zohlednit vliv 3D napjatosti betonu na jeho pevnost. Chování betonu při prostorové napjatosti je v 3D CSFM popsáno pomocí Mohr-Coulombovy teorie plasticity, která bude podrobněji rozebrána v následující kapitole. Betonářská výztuž je popsána bilineárním pracovním diagramem definovaným normou, viz Obr. 4d, se zohledněním již zmíněného tahového ztužení, viz Obr. 4b.

Soudržnost mezi výztuží a betonem je do modelu zavedena uvažováním zjednodušeného tuho-plastického vztahu dle Obr. 4f, přičemž f_bd je návrhová hodnota mezního napětí v soudržnosti specifikovaná normou pro dané podmínky soudržnosti. Zohledněny jsou i případné koncové úpravy výztuže (háky, apod.). Kotvy jsou modelovány obdobně jako betonářská výztuž. Přenos vodorovných sil z kotveného prvku do betonu je možné realizovat přímo kotvami, kontaktní plochou nebo smykovou zarážkou.

3.2 Mohr-Coulombova teorie plasticity v 3D CSFM

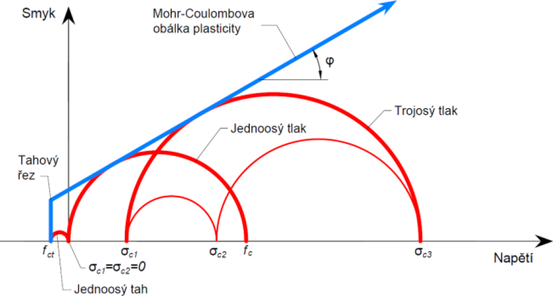
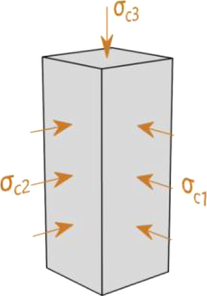
Nejvýznamnějším rozdílem 3D CSFM oproti stávající metodě CSFM je zavedení Mohr-Coulombovy teorie plasticity zohledňující trojosou napjatost v betonu. Mohr-Coulombova teorie je stavebním inženýrům známá především z oblasti geomechaniky, nicméně se jedná o matematický model, který se hodí i k popisu kvazi-křehkých materiálů jako např. betonu jakožto soudržného materiálu s vnitřním třením, který se pohybuje kolem cca 35–40˚.

V obecném tvaru lze pro daný úhel vnitřního tření betonu, vykreslit Mohrovy kružnice pro beton do známého obrázku (viz Obr. 5 vlevo). Modrá přímka představuje tzv. obálku plasticity a vymezuje oblast plasticky přípustných kombinací normálového a smykového napětí. Pokud leží celá Mohrova kružnice uvnitř přípustné oblasti, je materiál v pružném stavu.

a)

b)

Obr. 5: a) Mohr-Coloumbovy kružnice pro beton, b) trojosá napjatost

Lze si povšimnout, že s rostoucím hlavním napětím σ_c3 roste i maximální možný rozdíl mezi hodnotami σ_c3 a σ_c1, který definujeme jako ekvivalentní napětí σ_c,eq , tedy

Tento rozdíl vyjadřuje průměr Mohrovy kružnice a nazývá se deviátorem napětí.

Ekvivalentní hlavní napětí σc,eq vyjadřuje účinné jednoosé napětí pro obecný stav trojosé napjatosti.

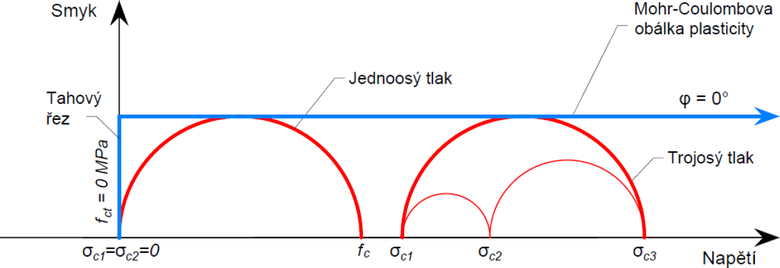
V metodě 3D CSFM je pro popis chování betonu uvažován úhel vnitřního tření φ = 0°. Tento předpoklad leží na bezpečné straně a představuje výrazné zjednodušení výpočtu při zachování dostatečně přesného modelu. Praktickým důsledkem zavedení nulového úhlu vnitřního tření je, že maximální možný rozdíl mezi σ_c3 a σ_c1 zůstává konstantní pro libovolnou hodnotu σ_c3 (viz Obr. 6) a hodnota σ_c,eq může být tedy přímo porovnávána s jednoosou únosností betonu v tlaku definovanou normami, nezávisle na velikosti σ_c3.

Obr. 6: Mohr-Coloumbovy kružnice pro beton použité v 3D CSFM

4. Praktické aplikace

Jedná se o nově vyvinutou metodu a v současné době se nacházíme v procesu její postupné verifikace, která je prováděna ve spolupráci s týmem prof. Kaufmana pod hlavičkou univerzity ETH v Zurichu.

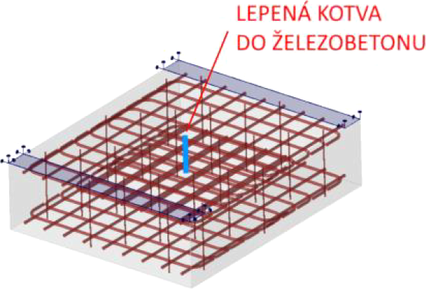
Jednou z pilotních verifikací metody 3D CSFM je výpočet kotev lepených v železobetonu, který je porovnáván s experimentem, s výpočtem v softwaru pro numerické simulace chování materiálů ABAQUS a také s posouzením podle návrhových norem, viz Obr. 7. Více se o výsledcích verifikace můžete dočíst zde [3]. Další provedenou verifikací je ověření trojosé napjatosti pro ovinutý a neovinutý beton, více např. zde [4], [5].

a)

b)

Obr. 7: Praktická aplikace 3D CSFM – kotvy lepené do betonu: a) model experimentu, b) model kotvení blízko okraje

Protože je metoda 3D CSFM obecná, není v principu nutné omezovat se pouze na návrh a posouzení kotvení. Lze například modelovat pilotové založení nebo zhlaví pilíře a další aplikace. Pro tento typ D-oblastí však zatím nebyla metoda plně verifikována.

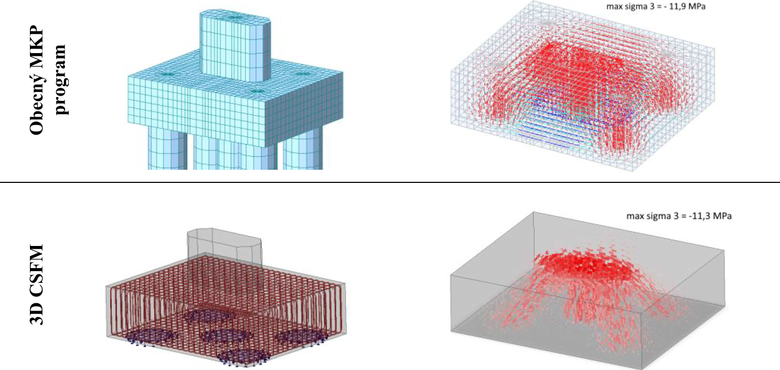
Na následujících obrázcích je zobrazen tok hlavních napětí v základu pro pilotové založení stanovené na prostorovém modelu v obecném MKP softwaru (izotropní materiál betonu, bez výztuže, lineární výpočet) s napětím stanoveným pomocí metody 3D CSFM (beton v tahu nepůsobí, výztuž, MNA). Hlava pilíře zde zatížena pouze tlakovou silou. V případě obecné MKP jsou v průběhu hlavních napětí patrná tahová napětí v betonu, která v modelu při použití metody 3D CSFM chybí (beton v tahu nepůsobí) a jsou zachycena výztuží. Dosažené hodnoty max. hlavních tlaků jsou v obou modelech srovnatelné.

Obecně však nelze očekávat přesnou shodu těchto dvou modelů, které jsou založeny na zcela rozdílných předpokladech.

Obr. 8: Pilotové založení

5. Závěr

Cílem příspěvku bylo čtenáře seznámit s novou rozšířenou metodou 3D CSFM a ukázat možnosti jejího praktického využití v praxi. Každého inženýra, zabývajícího se betonovými konstrukcemi, snad zaujal potenciál, který metoda nabízí. Potenciál, který spočívá především v usnadnění návrhu a posouzení velmi často diskutovaných D-oblastí, jejichž analýza není vždy jednoznačná a použití metody 3D CSFM pomůže rozptýlit pochybnosti a nabídnout projektantovi klidnější spánek.

Literatura

1. IDEA StatiCa Detail – Structural Design of Concrete 3D Discontinuities (BETA). IDEA StatiCa Support Center, 2024.
   https://www.ideastatica.com/support-center/idea-statica-detail-structural-design-of-concrete-3d-discontinuities-beta
2. KALÁB, P.: Navrhování D-oblastí v mostních konstrukcích pomocí CSFM. Silnice a železnice 01/2024
3. IDEA StatiCa Detail – Pullout behavior of cast-in-place anchors with different embedment depths. IDEA StatiCa Support Center, 2024.
   https://www.ideastatica.com/support-center/pullout-behavior-of-cast-in-place-anchors-with-different-embedment-depths
4. IDEA StatiCa Detail– Tri-axial stress – the active confinement effect. IDEA StatiCa Support Center, 2024.
   https://www.ideastatica.com/support-center/tri-axial-stress-the-active-confinement-effect
5. IDEA StatiCa Detail– Columns subjected to high compressive loading – Passive confinement effect. IDEA StatiCa Support Center, 2024.
   https://www.ideastatica.com/support-center/columns-subjected-to-high-compressive-loading-passive-confinement-effect