Vliv kotvení trubkového fasádního lešení na únosnost sloupku
Fasádní lešení patří mezi nejpoužívanější dočasné stavební konstrukce. Správné provedení kotvení patří k nejvýznamnějším krokům zajišťujícím bezpečné užívání lešení. Chybné provedení je zároveň častou příčinou poruch či havárií fasádního lešení. Článek popisuje vliv kotvení trubkového fasádního lešení na únosnost sloupku.
1. Úvod
Správně provedené kotvení fasádního lešení plní tři základní funkce:
- zajišťuje stabilitu lešení proti překlopení,
- přenáší vodorovné síly do přilehlého objektu,
- vymezuje vzpěrné délky sloupků.
V inženýrské praxi se bohužel poměrně často objevují neodborně smontované konstrukce, kdy je zejména třetí výše uvedená funkce kotvení podceněna. Lze se například setkat s názorem, že pokud nehrozí překlopení lešení (třeba opřením v horní úrovni), je lešení bezpečné. To je ovšem hrubé neporozumění funkci kotvení. V následujícím textu bude stručně zopakován obecný princip stanovení únosnosti sloupku a souvislost této únosnosti s rozmístěním kotev.
1.1 Stabilita ideálního prutu
Zejména u ocelových konstrukcí jsou velmi časté případy, kdy je tlačený konstrukční prvek štíhlý a při působení normálové síly se neporušuje prostým tlakem. Na jednoduchém příkladu bude demonstrováno, k jakému mechanismu porušení zde dochází.
Ideální svislý prut o délce L je kloubově uložený na obou koncích a zatížený osovou silou N (Obr. 1a). Ideálním prutem se rozumí prut nenarušený nepřesnostmi (imperfekcemi) geometrickými ani materiálovými. Pro zjednodušení lze předpokládat, že průřez je symetrický k oběma těžišťovým osám.
Předpokládejme, že síla N, která působí na prut, se postupně zvyšuje. Pokud je síla N < Ncr, prut je stabilní, což znamená, že při působení dočasného malého vodorovného impulzu sice může dojít k vychýlení prutu (Obr. 1b), ale po odeznění impulzu se prut vrátí do své původní polohy (Obr. 1c). Sílu Ncr označujeme jako kritickou sílu. V okamžiku, kdy síla N = Ncr (Obr. 1d) je prut v tzv. indiferentní rovnováze. Pokud nyní přestane působit vodorovný impulz, prut zůstává ve vychýlené poloze a při dalším zvýšení síly se stává nestabilním a dochází k jeho kolapsu. Hodnota kritické (Eulerovy) síly je pro ideální prut obecně
kde je
- Lcr
- tzv. kritická, neboli vzpěrná délka.
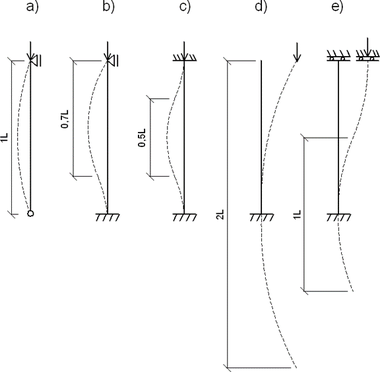
Správné stanovení vzpěrné délky patří mezi důležitý krok při určování vzpěrné únosnosti prutu. Vzpěrná délka závisí na uložení konců prutu, tzv. okrajových podmínkách. Základní případy jsou znázorněny na Obr. 2. Vzpěrnou délku je možné si představit jako vzdálenost dvou bodů (inflexních bodů sinusové půlvlny ohybové čáry po vybočení), kde příčným impulzem vybočený prut mění orientaci křivosti, neboli „kde se začíná ohýbat na druhou stranu“. K nalezení takového bodu je někdy potřeba průhybovou křivku prodloužit i mimo oblast původního prutu.
Na zřeteli je třeba mít skutečnost, že zatímco u krátkých prutů, u nichž se hovoří o namáhání prostým tlakem, dochází obvykle k porušení tlakovou silou, v případě vzpěrného tlaku se štíhlý prut ohýbá a k porušení dochází ztrátou stability a jeho přelomením.
K vybočení může dojít obecně v libovolném směru, zpravidla ve směru největší štíhlosti (viz dále), navíc může dojít ke ztrátě stability zkroucením (u nesymetrických průřezů, což se trubek netýká). Ve většině případů postačí posouzení stability ke dvěma těžišťovým osám. Vzpěrná délka může být (a u fasádních lešení je to běžné) pro vybočení kolmo ke každé ose jiná.
1.2 Štíhlost
Pro další výpočty se zavede bezrozměrná veličina „štíhlost“. Vyjádří se podle vztahu (2), resp. (3). U stabilitních výpočtů je nezbytné popisovat příslušné veličiny a charakteristiky správnými indexy.
kde je
- Lcr,y
- vzpěrná délka pro vybočení kolmo k ose y
- iy
- poloměr setrvačnosti k ose y.
Podobně
Kritickou sílu je potom možné vyjádřit s využitím štíhlosti vztahem:
kde je
- E
- modul pružnosti materiálu sloupku,
- I
- moment setrvačnosti průřezu a
- A
- průřezová plocha.
1.3 Vzpěrná únosnost skutečného celistvého prutu podle ČSN EN 1993-1-1 [3]
V části 1.1 a 1.2 byl popsán postup stanovení kritické síly pro ideální prut. Ideální prut je ovšem záležitostí čistě teoretickou. Skutečný prut vykazuje řadu počátečních odchylek a nedokonalostí (imperfekcí), které mají nepříznivý vliv na jeho vzpěrnou únosnost. Imperfekce mohou být geometrické (zakřivení, excentricita síly, nepřesnosti ve tvaru průřezu), strukturální (vlastní pnutí, odchylky pracovního diagramu) a konstrukční (zejména zabudování prutu v konstrukci – nedokonalé kloubové či tuhé připojení).
Protože vyčíslení všech těchto imperfekcí je prakticky nereálné, současné návrhové postupy (evropské normy) používají pro skutečný prut souhrnnou imperfekci ve smyslu geometrického zakřivení. Její velikost závisí zejména na tvaru průřezu a způsobu výroby prvku a prakticky se zavádí do tzv. křivek vzpěrné pevnosti. Trubky patří obecně mezi „příznivé“ průřezy, jejichž imperfekce jsou nízké.
To, že se jedná o vzpěrný tlak a nikoliv o tlak prostý, nám jednoduše určí stanovení poměrné štíhlosti:
kde je
- λ
- štíhlost prutu, viz (2) a (3),
- fy
- mez kluzu oceli.
Pokud tedy je poměrná štíhlost větší než 0,2, jedná se o vzpěrný tlak.
Tlačený prut se posuzuje podle podmínky
kde je
- NEd
- návrhová hodnota tlakové síly,
- Nb,Rd
- návrhová vzpěrná únosnost tlačeného prutu.
Vzpěrná únosnost je tedy odolnost prutu proti vybočení. Aby byla splněna podmínka únosnosti, musí být tato hodnota menší nebo rovna návrhové tlakové síle. Návrhová vzpěrná únosnost tlačeného prutu se určí z výrazu:
kde je
- χ
- součinitel vzpěrnosti (nejmenší z možných),
- γM₁
- dílčí součinitel spolehlivosti materiálu, podle Eurokódu 3 doporučená hodnota γM₁ = 1,0.
Hodnoty součinitele vzpěrnosti jsou ve formě vzpěrnostních křivek uvedeny v [3]. Pro osový tlak v prutu se hodnota součinitele vzpěrnosti pro odpovídající poměrnou štíhlost určí z příslušné křivky vzpěrné pevnosti. Zjednodušeně lze stanovit součinitel vzpěrnosti pomocí poměrné štíhlosti:
a následně z příslušných tabulek v závislosti na průřezu, materiálu, směru vybočení odečíst χy , χz.
2. Vzpěrná délka v závislosti na kotvení
Z předchozího popisu tedy vyplývá, že únosnost sloupku lešení (skutečného prutu) závisí na:
- průřezu sloupku,
- materiálu sloupku,
- vzpěrné délce.
První dva faktory konstruktér – lešenář zpravidla neovlivní (jsou dány typem použitého lešení), vzpěrná délka je potom pro výslednou únosnost sloupku naprosto zásadní. Význam kotvení pro stanovení únosnosti sloupku je dobře patrný z výpočetního postupu pro trubková lešení [2]. Ve statickém výpočtu se má uvažovat vzpěrná délka pro vybočení kolmo k fasádě podle kotevního rastru.
- kotvení ob jedno vodorovné ztužení (obr. 3a):
Lcr = 0,8L (10)
- kotvení v každém vodorovném ztužení (obr. 3b):
Lcr = L (11)
Za ztužení se přitom považují spojité podélníky v kombinaci s příčníky.
Únosnosti lešenářských trubek z oceli S235 pro různé vzpěrné délky udává následující tabulka.
| Vzpěrná délka Lcr [m] | Štíhlost λ | Součinitel vzpěrnosti χ | Návrhová únosnost NRd [kN] |
|---|---|---|---|
| 1,0 | 63 | 0,863 | 84,84 |
| 1,1 | 69 | 0,832 | 81,77 |
| 1,2 | 75 | 0,796 | 78,27 |
| 1,3 | 81 | 0,756 | 74,33 |
| 1,4 | 88 | 0,713 | 70,04 |
| 1,5 | 94 | 0,667 | 65,52 |
| 1,6 | 100 | 0,620 | 60,95 |
| 1,7 | 106 | 0,575 | 56,47 |
| 1,8 | 113 | 0,531 | 52,20 |
| 1,9 | 119 | 0,491 | 48,21 |
| 2,0 | 125 | 0,453 | 44,54 |
| 2,1 | 131 | 0,419 | 41,18 |
| 2,2 | 138 | 0,388 | 38,12 |
| 2,3 | 144 | 0,360 | 35,35 |
| 2,4 | 150 | 0,334 | 32,84 |
| 2,5 | 156 | 0,311 | 30,57 |
| 2,6 | 163 | 0,290 | 28,50 |
| 2,7 | 160 | 0,271 | 26,63 |
| 2,8 | 175 | 0,254 | 24,93 |
| 2,9 | 181 | 0,238 | 23,38 |
| 3,0 | 188 | 0,224 | 21,97 |
| 3,1 | 194 | 0,210 | 20,68 |
| 3,2 | 200 | 0,198 | 19,49 |
| 3,3 | 206 | 0,187 | 18,40 |
| 3,4 | 213 | 0,177 | 17,40 |
| 3,5 | 219 | 0,168 | 16,48 |
| 3,6 | 225 | 0,159 | 15,62 |
| 3,7 | 231 | 0,151 | 14,83 |
| 3,8 | 238 | 0,144 | 14,10 |
| 3,9 | 244 | 0,137 | 13,42 |
| 4,0 | 250 | 0,130 | 12,79 |
Pro kotvení po 2,0 m vychází únosnost 44,54 kN, pro kotvení ve dvojnásobné vzdálenosti 4,0 m vychází únosnost (pro Lcr = 0,8L = 3,2 m) 19,49 kN, tedy méně než poloviční.
U systémových lešení je výpočet výrazně komplikovanější, ovšem principy zde platí stejné: větší svislá vzdálenost kotev znamená nižší únosnost sloupku.
3. Analýza trubkového fasádního lešení
Jak bylo uvedeno v předchozí kapitole, při ručních výpočtech je uvažována vzpěrná délka sloupků podle typu kotvení hodnotou dle rovnic (10, 11). Odpovídají tyto hodnoty skutečnému chování konstrukce?
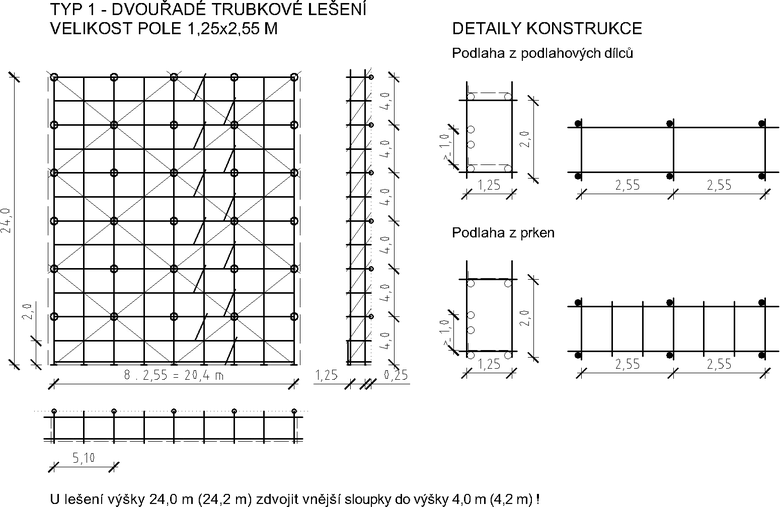
Cílem numerických výpočtů v [1] bylo ověřit platnost stávajících tradičních postupů. Pro tento účel byly vytvořeny sofistikovanější modely lešení hned v několika variantách. Bylo použito lešení z oceli S235JRG2, typ lešení 1 – dvouřadé trubkové lešení o velikosti polí 1,25 m × 2,55 m s celkovou výškou 24,0 m (obr. 4).
Výsledkem mělo být doporučení pro snadný a zároveň dostatečně výstižný výpočet. Pro výpočty byly požity softwary Nemetschek Scia Engineer 2012.0, Microsoft Office 2010 a metodika podle lešenářských i ocelářských norem.
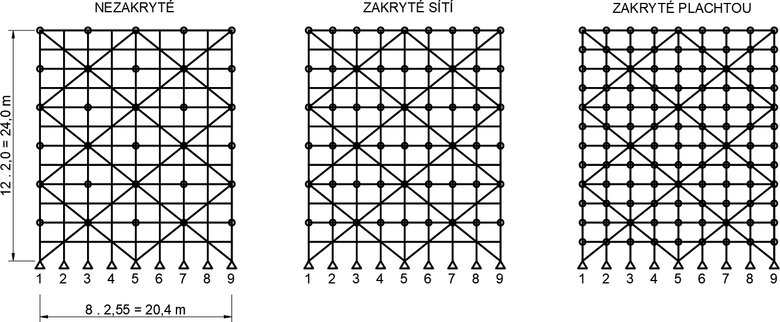
Jak již bylo zmíněno, kotvení zajišťuje jak globální stabilitu fasádního lešení, brání jeho překlopení, tak definuje vzpěrné délky sloupků. Kotevní rastr mimo jiné významně ovlivňuje fakt, zda se jedná o nezakryté lešení nebo lešení zakryté plachtou či sítí, jak si lze všimnout na obrázku č. 5. Obrázek zároveň znázorňuje použitý kotevní rastr v simulacích fasádního trubkového lešení.
Kotevní rastr pro nezakryté lešení je doporučen normou [2]. Ovšem kotevní rastr zakrytého lešení nepředepisuje norma, ten je dán spíše historickými zkušenostmi (dříve se ovšem zakrytí sítí či plachtou téměř nepoužívalo). Ačkoliv neexistuje předpis pro kotvení zakrytého lešení, vžila se v naší zemi jednoduchá pravidla. Při zakrytí sítí se počet kotev (oproti nezakrytému) zdvojnásobí – kotví se každá řada ve svislých vzdálenostech po 4 m) a při zakrytí plachtou se zčtyřnásobí – kotví se každý styčník.
3.1 Numerické modely
Modely byly rozděleny do několika variant numerických simulací. Výpočty byly provedeny na lešeních zakrytých sítí a plachtou a na lešením nezakrytém. U jednotlivých variant byl vždy posuzován kloubový, tuhý nebo pružný model s centrickými nebo excentrickými styčníky.
Modely byly tvořeny výhradně prutovými prvky. Sloupky, podélníky a prvky zábradlí byly modelovány jako spojité. Nastavovací spojky včetně jejich hmotnosti nebyly uvažovány. Jejich vliv je zanedbatelný nebo může být dokonce i příznivý.
Hlavní body numerických simulací:
- provedení lineárního výpočtu modelu bez imperfekcí,
- provedení stabilitního výpočtu,
- vyhodnocení výstižnosti vlastních stabilitních tvarů,
- vyhodnocení součinitele kritického zatížení α,
- stanovení celkové imperfekce,
- provedení geometricky nelineární analýzy konstrukce s imperfekcemi,
- posouzení průřezů,
- porovnání výsledků a další vyhodnocení.
3.2 Numerické modely nezakrytého lešení
Nezakryté lešení je namáháno nejmenší vodorovnou silou, proto byl použit kotevní rastr s nejmenším počtem kotev (obr. 5 vlevo). Všechny prvky byly doplněny o podpory zabraňující otáčení kolem podélné osy.
Postupně byly analyzovány tyto varianty:
- Kloubový model s centrickými styčníky
- Tuhý model s centrickými styčníky
- Tuhý model s excentrickými styčníky
- Pružný model s centrickými styčníky
- Pružný model s excentrickými styčníky
3.2.1 Kloubový model s centrickými styčníky
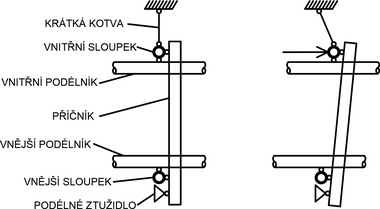
Prostorová tuhost trubkového nezakrytého lešení je zajištěna příhradovým ztužidlem na vnějším líci, příčnými ztužidly na bocích soustavy a spolupůsobením příčníků a podélníků se sloupky. Podle některých studií nelze upínacího účinku hákových spojek využít, protože je tuhost přípoje zanedbatelná. Pokud je upínací účinek spojek zanedbatelný, pak lze ovšem všechny spoje s hákovými spojkami považovat za kloubové. V případě standardního použití trubkového fasádního lešení je tím výrazně omezena tuhost lešení v rovinách podlah. Čím je tedy tuhost konstrukce v rovině podlah zajištěna? Na obr. 6 je vidět chování takovéhoto modelu při působení silového impulsu v oblastní vnitřního sloupku. Vodorovnému posunu sloupku, díky kloubovým přípojům příčníku není ničím bráněno a vzniká staticky přeurčitá konstrukce, tedy mechanismus.
To, že se jedná u tohoto modelu o mechanismus, bylo potvrzeno při stabilitní analýze (LBA). Analýza prokázala poměrně stabilní chování vnější řady sloupků (která byla ztužena podélným ztužidlem). Naproti tomu řada sloupků u fasády byla ve směru rovnoběžném s fasádou výrazně deformována, což ovšem neodpovídá praxi. Proto použití výhradně kloubového modelu není doporučeno.
3.2.2 Tuhý model
Na druhou stranu dalším extrémem se jevilo uvažovat přípoje podélníků, příčníků i kotev na sloupky jako ohybově tuhé. Bylo zřejmé, že se jednalo o limitní řešení a že skutečné chování konstrukce je někde mezi kloubovým a tuhým modelem. Byly porovnávány tuhé modely s centrickými a excentrickými styčníky.
Excentricita styčníků respektovala přesnou polohu trubek a jejich připojení pomocí hákových spojek.
Vzpěrná délka sloupku tuhého modelu vyšla dle předpokladů menší než vzpěrná délka uvažovaná normou [2]. Délka sloupků byla L = 4 000 mm.
3.2.3 Pružný model
Pružný model zohledňoval tuhosti přípojů na základě laboratorních zkoušek hodnotou c = 0,0063 MN/rad [1]. Nejpokročilejším modelem nezakrytého lešení byl pružný model s uvažovanou excentricitou styčníků.
Vzpěrná délka sloupku s pružnými centrickými styčníky vyšla nepatrně vyšší než vzpěrná délka uvažovaná normou [2]: Lcr = 0,835L pro L = 4 000 mm.
Výsledky modelování pružných modelů byly nejbližší zažité praxi s tím, že rozdíl mezi centrickým modelem a výrazně pracnějším excentrickým modelem není zásadní. U těchto modelů je ještě potřeba vždy prověřit, zda v místě styčníku nedochází k přemáhání hákových spojek v kroucení. Na základě výsledků [1] může být únosnost spojky v kroucení hodnotou 0,136 kNm.
3.3 Numerické modely zakrytého lešení
Kotevní rastr pro zakryté lešení sítí a plachtou je na obr. 5 uprostřed a vpravo.
3.3.1 Pružný model s excentrickými styčníky zakrytý sítí
Z provedených analýz bylo patrné, že sloupky lešení zakrytého sítí jsou významně namáhány ohybovým momentem a namáhání vzpěrným tlakem hraje pak při posouzení konstrukce menší roli než u nezakrytých konstrukcí. Vzpěrná délka při posouzení konstrukce odpovídala 0,832L . Namáhání od větru ovšem bylo takového rozsahu, že konstrukce zakryté sítí nevyhověly. Příčiny přemáhání sloupku ohybem mohou být následující:
- Zatížení větrem na zasíťované lešení podle Eurokódu je velmi konzervativní.
- Kotvení sloupku po 4 m je nedostatečné.
Tyto možné příčiny byly podrobeny další analýze na modelu, kde bylo kotvení ponecháno po 4 m výšky, ale rastr měl vystřídané rozmístění kotev. Tím byla zvýšena tuhost sloupků pomocí spolupůsobení mezilehlých pater kotvených u sousedních sloupků. Došlo ke snížení ohybového namáhání o 20 %, a tedy k mírnému zlepšení, ale sloupek opět nevyhověl. Vzpěrná délka se ale výrazně snížila, na 0,606L.
Lze tedy konstatovat, že zásadním problémem je stanovení velikost působícího zatížení od větru. Všeobecně je odbornou veřejností zatížení větrem podle základní lešenářské normy [4] považováno za příliš konzervativní.
3.3.2 Pružný model s excentrickými styčníky zakrytý plachtou
Tento model se od modelu zakrytého sítí lišil kotevním rastrem, který byl nejhustší. Vodorovné kotvení bylo provedeno v každém styčníku, viz obr. 5 vpravo. Výpočet probíhal ve všech fázích bez obtíží. Vzpěrná délka v tomto případě vyšla 0,954L.
4. Závěr
Mezi základní funkce kotvení fasádního lešení patří kromě přenosu sil do fasády a zajištění konstrukce proti překlopení také vymezení vzpěrné délky sloupku. Vzpěrná délka je potom základním faktorem přímo ovlivňujícím vzpěrnou únosnost sloupku.
Sloupek ve všech případech bezpečně vyhověl, kromě kloubového modelu. Z tohoto pohledu se jeví tradiční postup jako konzervativní, přestože uvažuje vzpěrnostní křivku „a“, zatímco podle ocelářské normy [3] se pro svařované trubky má používat křivka „c“. I vzpěrné délky odvozené ze stabilitních výpočtů vesměs potvrdily tradiční postup, kde se vzpěrná délka má uvažovat 0,8L.
Pro modelování trubkového lešení se ukázal kloubový model jako nefunkční a rovněž model s tuhými klouby nelze doporučit. Dochází zde k výraznému odklonu od skutečného chování konstrukce. Modely s pružnými styčníky doporučit lze, přičemž rozdíl mezi centrickým modelem a výrazně pracnějším excentrickým modelem není zásadní.
5. Poděkování
Související výzkum byl spolufinancován projektem SGS18/119/OHK1/2T/11. Autor tuto podporu vysoce oceňuje.
6. Normy a literatura
- Dolejš, J.; Prostorové spolupůsobení prvků a dílců fasádního lešení, Praha: ČVUT, Fakulta stavební, Katedra ocelových a dřevěných konstrukcí, Habilitační práce, 2012.
- ČSN 73 8107 Trubková lešení, ČNI 2005.
- ČSN EN 1993-1-1 Eurokód 3: Navrhování ocelových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. ÚNMZ 2011.
- ČSN EN 12811-1 (73 8123) Dočasné stavební konstrukce – Část 1: Pracovní lešení – Požadavky na provedení a obecný návrh, ČNI 2004.
In this paper the influence of anchoring on the load-bearing capacity of the façade scaffolding standard is described. Proper execution of anchoring belongs to the most important steps to ensure the safety of the use of scaffolding. It is also one of the most common cause of façade scaffolding failures and accidents in practice. The paper compares original approaches of anchoring design according to scaffolding standards and advanced numerical analysis. The research was carried out on uncovered scaffolding and on a scaffolding with sheetinh or netting. The buckling lengths derived from stability calculations generally confirmed the traditional procedure where the buckling length should be considered as 0.8L. Models with elastic joints correspond most to the real behavior of the structure. According to the results of numerical simulations, the behavior of a covered scaffold does not match either the net covered or the sail covered. The standard is loaded mainly by a bending caused by an extreme wind acting perpendicular to the façade with respect to the anchor grid.
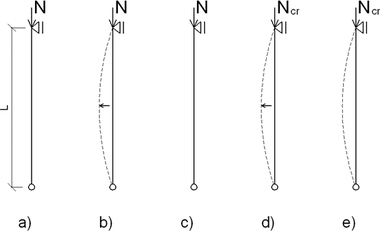
![Obr. 3 – Stanovení vzpěrné délky sloupku podle ČSN 73 8107 [2]](/docu/clanky/0199/019977o15.png)