Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

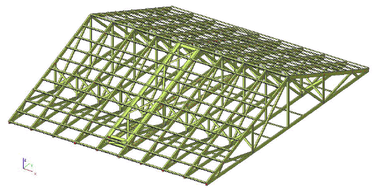
Význam ztužení při návrhu a realizaci vazníkových konstrukcí

25.6.2012

doc. Ing. Petr Kuklík, CSc., Ing. Aleš Tajbr, ČVUT v Praze, Stavební fakulta

Recenzovaný

Dřevěné vazníky jsou hojně navrhovány na zastřešení rodinných domů i průmyslových a prodejních objektů. Předností technologie využívající ke spojování jednotlivých dřevěných prvků styčníkovou desku s prolisovanými trny je vysoká pevnost a tuhost připojení, která dovoluje bezpečný návrh těchto subtilních konstrukcí na zajímavá rozpětí. Vazníky jsou navrhovány ve specializovaných programech jako rovinné konstrukce zatížené výhradně ve své rovině. Vodorovné zatížení, které působí kolmo na rovinu vazníků, musí být přeneseno systémem ztužidel do podpor.

Úvod

Návrh systému ztužení

Zajištění dostatečné prostorové tuhosti rovinných příhradových konstrukcí je nezbytnou a zásadní podmínkou spolehlivosti každé příhradové konstrukce. Právě proto musíme konstrukce s dřevěnými vazníky s kovovými deskami s prolisovanými trny vhodně vyztužit. Funkci ztužidel můžeme obecně shrnout do následujících tří bodů [1]:

Zajištění dostatečné prostorové tuhosti konstrukce a přenosu vodorovných zatížení.
Zajištění tvaru a polohy konstrukce.
Zajištění stability tlačených prvků i celé konstrukce.

V závislosti na době instalace ztužujících prvků do konstrukce rozeznáváme ztužení montážní, které slouží především k zajištění polohy, svislostí a roztečí vazníků při montáži, a trvalé, které plní tři výše uvedené body po celou dobu životnosti konstrukce.

Často se v praxi setkáváme s projekty, kde systém ztužení a zavětrování konstrukce není navržen vůbec a jeho návrh a realizace jsou ponechány na firmě vyrábějící nebo montující vazníky. Bohužel právě ztužení představuje celosvětově největší problém dřevěných konstrukcí s deskami s prolisovanými trny. Z části je to způsobeno nedostatečnou informovaností odborné i laické veřejnosti (investorů), snahou výrobních firem o snížení nákladů a absencí technologické předpisu popisující správný návrh a realizaci ztužujícího systému vazníkové konstrukce.

Pro soustavu několika rovnoběžných vazníků je klíčové příčné ztužidlo (někdy označováno jako ztužidlové pole nebo tuhá dvojice), které dodává potřebnou tuhost spojovacím prvkům kolmým na vazníky (např. střešní latě na horním pásu a rošt pro sádrokarton na spodním pásu). To potvrdily i experimenty v měřítku 1:1 na konstrukci 22 sedlových vazníků zaměřené na zjištění příspěvku jednotlivých prvků zavětrování do tuhosti celé vazníkové konstrukce, které ve Velké Británii provedl Bainbridge se svým týmem [2]. V Jihoafrické republice se intenzivním výzkumem příčných ztužidel zabývá dvojice vědců Burdzik a Dekker, kteří v návaznosti na několik havárií vazníkových konstrukcí v důsledku absence ztužení definují nová pravidla pro vyztužení střešní roviny pomocí lisovaných ztužidel [3].

Typickým prvkem ztužidlového pole (příčného vyztužení konstrukce) je lisované ztužidlo horního pásu, které je navrhováno jako prostě podepřený příhradový nosník na rozvinutou délku horních pásů vazníků. Nosník může být zatížen jak účinky větru (např. vítr působící na štít nebo třecí složka podélného větru), tak účinky stabilizačního zatížení, které se vypočítá podle vztahu:

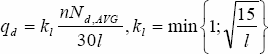
kde

q_d: – návrhová hodnota rovnoměrného stabilizačního zatížení ztužidla [kN/m],
k_l: – součinitel zohledňující kvalitu výroby a montáže,
n: – počet ztužovaných vazníků,
N_d,AVG: – průměrná návrhová síla v horních pásech ztužovaných vazníků [kN],
l: – rozvinutá délka ztužidlového pole [m].

Průhyb ztužidla je limitován 1/700 jeho rozpětí pro účinky pouze stabilizačního zatížení nebo 1/500 rozpětí pro společné účinky větru a stabilizačního zatížení [4]. Toto omezení vodorovné deformace ztužidla představuje skrytý požadavek na jeho minimální tuhost – viz odvození vztahu pro výpočet stabilizačního zatížení [5].

Zatěžovací zkoušky ztužidlových polí

Katedra Ocelových a dřevěných konstrukcí, Stavební fakulta ČVUT v Praze se ve spolupráci se společností Vazníky D.N.K. s.r.o. provedla v roce 2009 zatěžovací zkoušky třech různých typů ztužidlových polí (ZP1, ZP2 a ZP3) s cílem analyzovat jejich chování při působení vodorovného zatížení [6]. Délka vazníků byla délka 11 m (rozpětí 10 m, přesah 0,5 m na každé straně), sklon 22°, tloušťka 50 mm a osová vzdálenost 1,0 m. Ztužidlo horního pásu bylo navrženo na stabilizační zatížení vyvozené 10 vazníky; pásy byly tvořeny profily 50/120 mm, diagonály 50/80 mm.

Obr. 1 – Zatěžovací zkouška ZP1 – maximální zatížení 1320 kg

ZP1 bylo realizováno s lisovanými ztužidly v rovině horního i dolního pásu a lisovaným nadpodporovým ztužidlem, která byla k vazníkům průběžně připojena hřebíky 4/120 mm. Ve vrcholu byla ztužidla spojena ocelovou páskou, aby byl zajištěn přenos tahových sil. Kotvení konstrukce bylo posíleno v souladu se standardními detaily používanými společností Vazníky D.N.K. s.r.o. V případě ZP2 byla lisovaná ztužidla nahrazena zkříženými prkny 32/100 mm (tzv. Ondřejskými kříži) v příslušných rovinách. Konstrukce ZP3 byla navržena jako kombinace ZP1 a ZP2 – ztužidlo horního pásu bylo lisované a ztužidlo spodního pásu bylo vybité z Ondřejských křížů.

Obr. 2 – Posílené kotvení a spojení ztužidel ve vrcholu – ZP1

Jednotlivé testované konstrukce byly smontovány, ukotveny a poté zatěžovány v bodech A, B a C vodorovnou silou známé velikosti. Během zkoušky byla průběžně měřena vodorovná deformace a to jak ve vrcholu vazníku (bod B) tak v místě styčníku horního pásu a svislic (body A a C). Všechny tři konstrukce byly v posledním kroku ponechány pod zatížením do druhého dne, tedy minimálně 15 hodin, za účelem zjištění vlivu dotvarování.

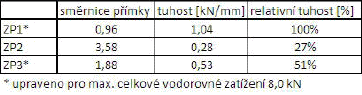
Tabulka 1 – Porovnání relativních tuhostí ZP1, ZP2 a ZP3

Výsledky všech tří zatěžovacích zkoušek jsou shrnuty v následujícím grafu, ve kterém jsou navíc zobrazeny limitní deformace ztužidla – vodorovné přímky odpovídající 1/500 a 1/700 délky ztužidla střešní roviny. Čára ZH-TRUSS popisuje chování modelu ztužidla roviny horního pásu, které bylo navrženo pro ZP1 v programu TRUSS 2D a které bylo zatíženo stejným způsobem jako testované konstrukce. Svislá přímka, která přísluší hodnotě 9,5 kN, vyjadřuje velikost náhradního rovnoměrného zatížení na ztužidlo spočtenou dle ČSN EN 1995-1-1 [4] pro 10 vazníků V1 (0,89 kN/m) a vynásobenou délkou ztužidla horního pásu. Z grafu je patrné, že ZP1 vykazuje nejvyšší tuhost a chová se nejvíce lineárně ze všech tří typů testovaných ztužidlových polí. Pouze ZP1 se přibližuje požadavku normy na limitní průhyb l / 700 pro tuto hodnotu zatížení. V tabulce č. 1 jsou uvedeny směrnice proložených přímek pro bod B všech tří typů ztužidlových polí. Pro ZP1 a ZP3 byly hodnoty upraveny pro data pouze do hodnoty celkového vodorovného zatížení 8,0 kN, aby bylo srovnání s tuhostí ZP2 objektivní.

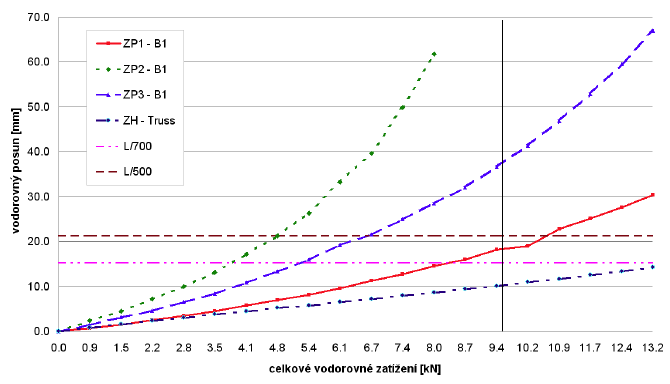
Obr. 3 – Graf závislosti deformace ve vrcholu (bod B) na vodorovném zatížení pro ZP1, ZP2 a ZP3

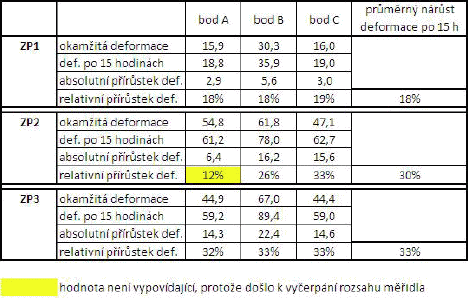
Tabulka 2 – Nárůst vodorovné deformace konstrukce po 15 hodinách v zatíženém stavu

Posledním měřením, které bylo u každé testované konstrukce provedeno před odtížením, byl odečet deformace druhý den ráno, tedy po 15 hodinách od vnesení posledního zatížení. Naměřené hodnoty a výsledky z nich plynoucí jsou uvedeny v tabulce č. 2 a je z nich zřejmé, že ZP1 vykazuje téměř dvakrát nižší procentuální nárůst deformace zatížené konstrukce v čase než zbylé dvě testované konstrukce.

Numerický model konstrukce

Pro konstrukce ZP1 a ZP2 byl vytvořen prostorový počítačový model konstrukce v programu Scia Engineer, který laskavě zapůjčila firma SCIA CZ s.r.o. Cílem úlohy je získání relativně přesné představy o chování obou konstrukcí, porovnání vypočtených a naměřených výsledků a analýza příčiny případných odchylek. Základní geometrický podklad pro model vazníku byl převzat z prutového statického schématu vazníku z programu TRUSS. Jednotlivým prutům byly přiřazeny příslušné průřezy a zároveň i materiálové vlastnosti dřeva. Veškeré prvky jsou modelovány jako vetknuté ve své rovině a kloubově uložené v rovině kolmé. Horní a dolní pásy jsou modelovány jako průběžné, bez ohledu na polohu styčníku nastavení. Vazník je podepřen prostě – tedy kloub, posuvný kloub se zabráněním deformace z roviny. Osová vzdálenost vazníků je 1,0 m, stejně jako v zatěžovací zkoušce. Obě konstrukce jsou stejnoměrně bodově zatíženy v místě styku svislic a horních pásů na jednom z vazníků. Přírůstek zatížení je 0,5 kN v každém kroku a v každém zatěžovacím místě.

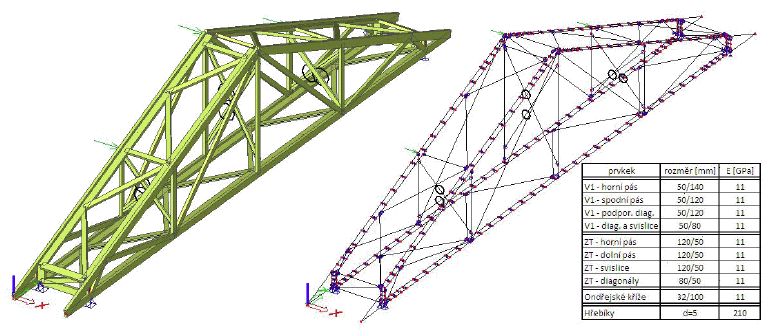
Obr. 4 – Model konstrukce ZP1 v programu Scia Engineer

V případě ZP1 jsou mezi dva sousedící vazníky vložena ztužidla horních a dolních pásů a nadpodporová ztužidla. Spojení jednotlivých typů ztužidel je provedeno prostřednictvím společného prvku – například horního pásu nadpodporového ztužidla a krajní svislice ztužidla horního pásu. Pásové prvky ztužidel jsou připojeny k vazníku pouze hřebíky průměru 5 mm. Žádné jiné spojení mezi vazníkem a ztužidly nebylo modelováno.

Hřebíky jsou uvažovány jako oboustranně vetknuté pruty, s pružným posuvem na konci připojeném k vazníku ve směru osy y a z lokálního souřadného systému dílce. Pružné uložení simuluje prokluz spoje, který byl vypočítán podle vztahu:

K_ser = ρ_m^1,5d ^0,8 / 30 = 420^1,5 . 5^0,8 / 30 = 1040 [N/mm]

Ondřejské kříže jsou vymodelovány z profilu 32/100 mm a je použit speciální typ prvku, který umožňuje pouze přenos osových sil. Na obou koncích jsou prvky Ondřejských křížů připojeny k vazníku kloubově a pružným kontaktem s tuhostí ve směru lokální osy x, která odpovídá 2 ks hřebíků 3,55/90 mm a simuluje prokluz hřebíkového spoje pod zatížením:

2 . K_ser = 2 . ρ_m^1,5d ^0,8 / 30 = 2 . 420^1,5 . 3,55^0,8 / 30 = 2 . 790,5 = 1581 [N/mm]

V modelu jsou zohledněny excentricity připojení prvků zavětrování k vazníku – bylo uvažováno s minimální excentricitou 200 mm. Před samotným výpočtem bylo nastaveno zjemnění standardně generované sítě na 10 prvků na každý prut. Lineární výpočet je proveden na základě metody konečných prvků.

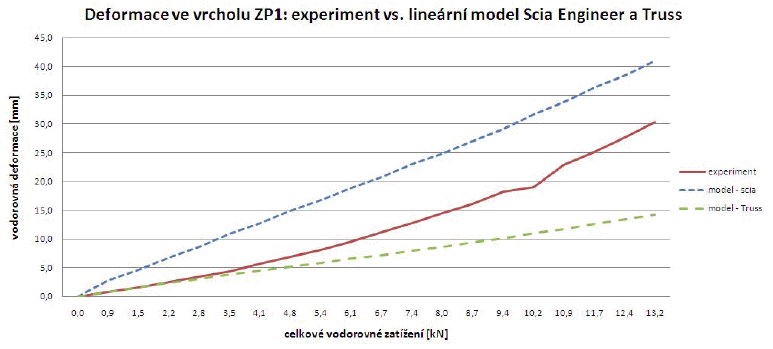
Obr. 5 – Srovnávací graf závislosti vodorovné deformace ve vrcholu ZP1 pro experimentální data a lineární modely v programech Scia Engineer a Truss

Konfrontací chování prostorového modelu v programu Scia Engineer s výsledky experimentu se zejména pro nižší hodnoty zatížení ukazuje, že jeho tuhost je výrazně nižší. To může být zčásti způsobeno tím, že v modelu není uvažován jakýkoliv přenos sil třením mezi pásy ztužidel a vazníků, které bezpochyby hraje určitou úlohu. Tento rozdíl v tuhosti je postupně redukován. V závěrečné části grafu lze pozorovat, že obě čáry jsou rovnoběžné. Čára „model-Truss“ kopíruje experimentální křivku velmi dobře zejména v počátečních krocích experimentu, kdy se vzorek chová lineárně.

V případě ZP2 jsou dva sousední vazníky spojeny Ondřejskými kříži 32/100 mm a dlouhými podélnými výztuhami 30/50 mm v rovině horního a dolního pásu. Tyto prvky jsou modelovány stejným způsobem jako Ondřejské kříže v modelu ZP1 – tedy přenos pouze osových sil, kloubové uložení a lineárně pružné chování hřebíkového přípoje ve směru osy prutu Ondřejského kříže. Posun každého hřebíkového spoje je limitován hodnotou 2 mm. Po dosažení této hodnoty se již nezvyšuje přenášené zatížení. Je použit bilineární pracovní diagram hřebíkového spoje. Tento typ přípoje lze v programu Scia Engineer použít pouze ve spojení s nelineárním typem výpočtu, pro který byla využita Timoschenkova metoda.

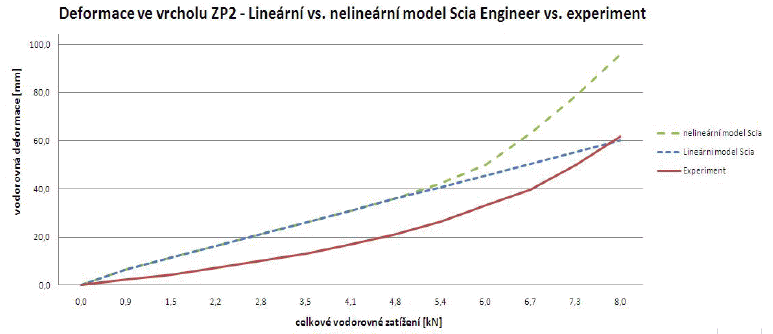
Obr. 6 – Srovnávací graf závislosti vodorovné deformace ve vrcholu ZP2 pro experimentální data a lineární a nelineární model v programu Scia Engineer

Na obrázku č. 6 jsou uvedeny výsledky jak pro lineární, tak pro nelineární výpočet. Obě větve se od sebe oddělí při celkovém zatížení cca 5 kN, kdy je dosažen maximální dovolený posun v některém z hřebíkových přípojů. Podobně jako v případě ZP1 je i zde podhodnocena počáteční tuhost soustavy. Lineární model protne experimentální křivku téměř přesně v okamžiku přerušení zatěžovací zkoušky. To sice nevypovídá příliš o kvalitě modelu, ale jasně to ukazuje na nelineární chování testované konstrukce. Nelineární model překvapivě dobře popisuje chování zkoušeného vzorku v závěrečných krocích zkoušky, obzvlášť pokud bychom vzali do úvahy hodnoty naměřené v posledním kroku druhý den ráno (ve vrcholu ZP2 to bylo 78,0 mm).

Obr. 7 – Model sedlové střechy se ZP1

Pro dokonalejší představu o chování ztužidlového pole v reálné konstrukci byl vytvořen numerický model sedlové střechy v programu Scia Engineer – viz obrázek č. 7. Konstrukce je variantně modelována s lisovaným ztužidlovým polem (ZP1) a se ztužidlovým polem s Ondřejskými kříži (ZP2). Cílem vypracování modelů obou variant je vzájemné porovnání jejich chování. Vazníky jsou modelovány včetně vodorovné imperfekce horního a spodního pásu kolmo na rovinu vazníku ve tvaru kruhové úseče s maximální hodnotou l / 300. U všech vazníků je počáteční výchylka orientována na jednu stranu – ve směru globální osy X.

V modelu není uvažováno s možnou odchylkou vazníku od svislice, která se ale v praxi poměrně často vyskytuje.

Podobně jako v předchozích modelech samostatných ztužidlových polí jsou vazníky zavětrovány Ondřejskými kříži, které jsou excentricky připojeny k vazníkům dvěma hřebíky. Tomuto kloubovému přípoji je opět přiřazen bilineární pracovní diagram a jeho deformace je omezena maximální hodnotou 2 mm. V modelu se dále objevují střešní latě profilu 30/50 mm, které jsou kloubově a excentricky připojeny k horním pásům vazníků. Ve spoji je uvažováno pouze s jedním hřebíkem – tuhost tohoto spoje je poloviční než tuhost přípoje Ondřejského kříže. V základním modelu bylo uvažováno s osovou vzdáleností latí 60 cm, poté byla vytvořena i varianta s laťováním po 30 cm. Na konstrukci působí pouze svislé liniové zatížení, které je aplikováno přímo na horní pásy vazníků. Zatížení je krokově zvyšováno po 0,25 kN/m až do chvíle, kdy se dojde k porušení některého z prvků nebo přípojů. Průběžně je sledována vodorovná výchylka (ve směru globální osy X) celé konstrukce, především horních pásů krajního vazníku, kde se objevují největší vodorovné deformace. Pro obě konstrukce je použit nelineární výpočet, který v programu Scia Engineer uvažuje uživatelsky definované limitní deformace přípojů a jejich pružno-plastické chování. Pochopitelně tento typ výpočtu respektuje teorii druhého řádu a byla pro něj zvolena iterativní Newton-Raphsonova metoda.

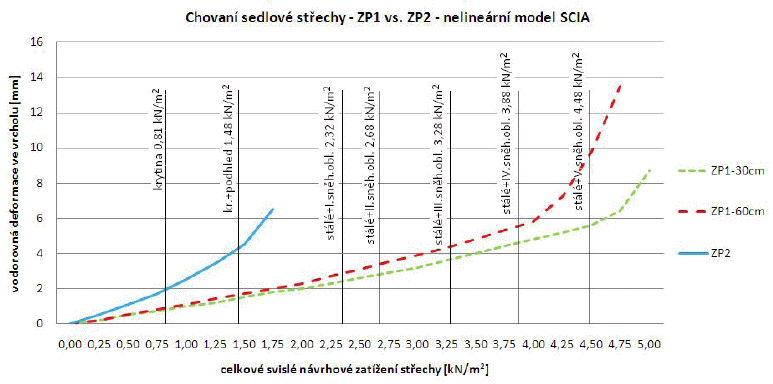
Obr. 8 – Vodorovná deformace sedlové střechy se ZP1 resp. ZP2 v závislosti na svislém zatížení

Z grafu na obrázku č. 8 je zřejmé, že vodorovná tuhost konstrukce modelované sedlové střechy se ZP1 je vyšší, přenesené zatížení je také vyšší a vodorovné deformace této konstrukce kolmo na rovinu vazníků jsou pro srovnatelné úrovně zatížení nižší než u konstrukce se ZP2. Zde se naplno projevuje pružno-plastické chování hřebíkového přípoje Ondřejských křížů ve střešní rovině, kde velmi brzo dojde k vyčerpání kapacity tohoto spoje – deformace roste a již se nezvyšuje přenášené zatížení. Oproti tomu se konstrukce s lisovaným ztužidlem chová víceméně lineárně až do úrovně zatížení 4,0 kN/m². Nepatrně vyšší vodorovnou tuhost vykazuje konstrukce se ZP1 a laťováním po 30 cm. Pro ilustraci jsou v grafu vyznačeny úrovně návrhového zatížení odpovídající zatížení krytinou, podhledem a sněhem ve sněhových oblastech dle ČSN EN 1991-1-3. Maximální hodnota vodorovné deformace ztužidla dle ČN EN 1995-1-1 je 15,2 mm (l / 700). Této hodnoty nedosáhla ani jedna z modelovaných konstrukcí.

Numerické modelování konstrukce samostatných ztužidlových polí i celých konstrukcí sedlových střech potvrdilo výsledky, které byly dosaženy v experimentální části. Konkrétně bylo ověřeno, že ztužidlové pole s lisovanými ztužidly (ZP1) má vyšší vodorovnou tuhost než ztužidlové pole s Ondřejskými kříži (ZP2). V modelu sedlové střechy se tento fakt projeví vyšší vodorovnou tuhostí celé konstrukce a vyšším přeneseným zatížením.

Závěr

Výsledky experimentální i numerické části zkoušky jasně dokazují, že lisovaná ztužidla výrazným způsobem přispívají k celkové tuhosti střešních konstrukcí z dřevěných vazníků s kovovými deskami s prolisovanými trny. Používání těchto ztužidel v kombinaci s dalšími ztužujícími prvky a vhodnými detaily by mělo být standardizováno, zakotveno v příslušných technických předpisech a vyžadováno při realizacích.

Poděkování

Tento příspěvek byl vytvořen za podpory projektu výzkumu a vývoje ČVUT v Praze MSM 6840770005 „Udržitelná výstavba“ a ve spolupráci s firmou Vazníky D.N.K. s.r.o.

Literatura

[1] KUKLÍK, P., TAJBR, A., VODOLAN M.: Prostorová tuhost dřevěných střešních konstrukcí s kovovými deskami s prolisovanými trny. Sborník semináře Dřevostavby 2007. VOŠ a SPŠ Volyně. 2007
[2] BAINBRIDGE R.J. et al. Stability bracing for non-domestic timber trussed rafter roofs. The Structural Engineer Volume 76/ No. 17. 1998
[3] BURDZIK W.M.G., DEKKER N.W.: Comparison between bracing requirements using various codes and a proposed new set of bracing criteria. Journal of South African Institution of Civil Engineering, 42(1): str. 11–15. Jihoafrická republika. 2000
[4] ČSN EN 1995-1-1 – Eurokód 5: Navrhování dřevěných konstrukcí, ČNI, Praha, 2006
[5] KOŽELOUH B.: Dřevěné konstrukce podle Eurokódu 5: STEP 1. KODR. Zlín. 1998
[6] KUKLÍK P., TAJBR A.: Vodorovná tuhost ztužidlových polí lehkých dřevěných střešních konstrukcí s kovovými deskami s prolisovanými trny. Sborník přednášek z odborného semináře Dřevostavby. VOŠ a SPŠ Volyně. 2009

English Synopsis

The importance of reinforcement in the design and implementation of truss structures

Timber trusses with punched metal plate fasteners are designed as plane structures loaded only in their plane. Actions applied perpendicularly to the truss plane must be transferred by engineered bracing system. Correct design of the bracing system is considered to be one of the essential conditions providing required reliability of the whole roof structure. The CTU in Prague, Faculty of Civil Engineering, Department of Steel and Timber Structures in cooperation with company Vazníky D.N.K. s.r.o. have performed load tests of three different types of engineered bracing truss structures. The aim of the tests was to describe behaviour of the specimen under horizontal load. Numerical model of two common types of bracing frames and a model of a whole roof consisting of 10 timber trusses was made to verify the results obtained from the experiment.