Statistické posouzení kvantitativních jakostních parametrů stavebních výrobků při posuzování shody a certifikaci v oblasti požární ochrany
Článek navrhuje statistické postupy pro vyhodnocení zkušebně stanovených kvantitativních jakostních parametrů stavebních výrobků k objektivizaci rozhodnutí při posuzování shody/certifikaci v oblasti požární ochrany. Postup lze využít i pro jiné typy výrobků a při výzkumu/vývoji nových materiálových výrobků.
Úvod
Na český trh stavebních výrobků se vztahují mj. zákon č. 22/1997 Sb., [1] a nařízení vlády (NV) č. 163/2002 Sb. [2]. NV ukládá povinnost též posoudit tzv „stanovené výrobky“. Výrobce je povinen prokázat jejich shodu s příslušnými předmětovými normami. Postup přináší ochranu spotřebitele z hlediska ochrany zdraví, požární bezpečnosti, hygieny, úspory energie a ochrany životního prostředí.
Příl. 2 nařízení vlády uvádí následující hlavní skupiny stanovených výrobků k posuzování shody:
- Stavební výrobky pro betonové a železobetonové části staveb,
- Stavební výrobky pro zděné stavby
- Stavební výrobky ze dřeva a dřevěné konstrukce
- Stavební výrobky pro kovové konstrukce
- Ochranné, tepelně izolační materiály a výrobky, hydroizolační materiály, střešní krytiny a lepidla
- Stavební výrobky ze skla
- Stavební výrobky pro kanalizační systémy a rozvody kapalin a plynů
- Stavební výrobky pro otvorové výplně
- Zvláštní materiály, výrobky, konstrukce a zařízení
- Technická zařízení staveb
- Stavební výrobky pro vnitřní a vnější povrchové úpravy stěn, stropů, podlah
- Stavební výrobky pro hygienická zařízení a ostatní speciální výrobky.
Na evropský trh stavebních výrobků se vztahuje též nařízení Evropského parlamentu a Rady (EU) č. 305/2011 (CPR) [3]. Povinnost posouzení podle tohoto nařízení nastává v případě, že jsou na výrobky stanoveny požadavky v harmonizovaných českých (evropských) technických normách a/nebo evropských technických posouzeních (ETA). Po splnění stanovených požadavků jsou výrobci oprávněni označovat své výrobky značkou CE (CCZ je českou značkou shody).
Významným nástrojem k objektivnímu rozhodnutí, zda výrobek splňuje/nesplňuje stanovené jakostní kvantitativní parametry je statistické posouzení jejich hodnot zkušebně stanovených podle předepsaných zkušebních norem.
1. Statistické posouzení kvantitativních výsledků zkušebních stanovení
Kvalitu materiálových stavebních výrobků lze charakterizovat zkouškou jakostní vlastnosti např. M, která má u kvalitního výrobku určitou hodnotu např. M0. Pokud při ověřování vlastnosti M při certifikaci/posuzování shody byla u dodaného vzorku výrobku zjištěna hodnota M = M0 ± U, je potvrzena jeho kvalita a certifikát mu může být udělen. U je přípustná tolerance výsledku.
V opačném případě, pokud je M < M0 − Δ, nebo když M > M0 + Δ, a Δ je > U, nepotvrdila se jeho jakost a certifikát mu udělen být nemůže.
Zkušební normovaná metoda obvykle vyžaduje měření vlastnosti výrobku M opakovaně nkrát s konkrétními číselnými výsledky X1, X2, …, Xn.
Výsledky Xi (i = 1,2,…, n) nejsou rovny M, ale mají hodnoty Xi = M + ui, kde ui jsou jednotlivé nejistoty měření. Předpokládáme, že naměřené výsledky byly/jsou statisticky posouzeny na odlehlost a vybočenost a že odlehlé hodnoty byly / jsou vyloučeny [5]. Pokud jsou tyto nejistoty navzájem nezávislé a mají normální rozdělení se střední hodnotou Θ a s rozptylem σ2, respektive směrodatnou odchylkou σ, potom lze použít k hodnocení výsledků zkoušek následující postup:
určí se tzv. interval spolehlivosti (konfidenční interval) pro hodnotu M tak, aby platilo:
P (M̅ ≥ M) ≐ 1 − α /2, tj. P (M̅ < M) ≐ α /2,
potom P (M̲̲ ≤ M ≤ M̅) ≐ 1 − α,
Pravděpodobnost, že interval nebude obsahovat skutečnou hodnotu, je přibližně α.
Číslo (1 − α), zvolené podle závažnosti následků omylů (zpravidla 0,90 nebo 0,95 či 0,99), je tzv. koeficient spolehlivosti (konfidenční koeficient). Jeho doplněk do 1 rovný α je tzv. riziko omylu.
Za daných předpokladů (normalita rozdělení chyb) má interval spolehlivosti tvar
− μ1 − α /2 
, M̅ = + μ1 − α /2 ,
kde je výběrový aritmetický průměr výsledků
= 
(x1 + x2 + … + xn)
a μ1 − α /2 je tzv. kvantil standardního normálního rozdělení, definovaný vztahem
Pro nejběžnější hodnoty α (0,1 nebo 0,05 či 0,01) jsou velikosti těchto kvantil uvedeny v následující tabulce [6]
| α | 1 − α /2 | M1 − α /2 |
|---|---|---|
| 0,01 | 0,995 | 2,576 |
| 0,05 | 0,975 | 1,960 |
| 0,1 | 0,950 | 1,645 |
| 0,2 | 0,900 | 1,282 |
Rozhodování o způsobilosti výrobku k danému účelu/shodě by mohlo být následující:
-
M̅ > MH = M0 + Δ,tj. není vyloučena možnost, že M > MH, proto výrobek nesplňuje kvalitativní kritérium a nelze ho schválit,
-
M̲̲ < MD = M0 − Δ,
tj. není vyloučena možnost M < MD. Opět výrobek nesplňuje kritérium kvality a nelze ho schválit,
-
MD < M̲̲ < M̅ < MH
znamená s vysokou pravděpodobností, že je M mezi přípustnými hodnotami MD a MH, a proto lze výrobek schválit.
Stupeň ochrany před možným omylem lze vyjádřit takto:
- je-li ve skutečnosti M > MH = M0 + Δ, potom s vysokou předem zvolenou pravděpodobností 1 − α /2 bude M > MH a pokud je M̅ > MH , výrobek je s vysokou pravděpodobností potřebné neschválit,
- pokud je M < MD = M0 − Δ, potom s pravděpodobností 1 − α /2 bude M̲̲ < MD a výrobek je nutno též neschválit,
- je-li ve skutečnosti M ≐ M0 (M se rovná správné hodnotě M0), potom s vysokou pravděpodobností 1 − α bude MD < M̲̲ < M0 < M̅ < MH a výrobek lze schválit (zdůvodněné správné rozhodnutí).
Nepříjemná/nerozhodná situace může nastat, když interval spolehlivosti (M̲̲, M̅) obsahuje jak hodnotu M0, tak i některou z hodnot MD, MH. V tom případě nelze vyloučit ani možnost M = M0 (správná hodnota), ani M < MD (M má příliš nízkou hodnotu), případně M > MH (M má příliš vysokou hodnotu). Této situaci se lze vyhnout, když se zvolí počet měření n tak, aby délka intervalu spolehlivosti d = M̲̲ − M̅ byla menší než číslice Δ, tj. když se položí
}
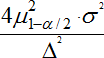Jednoduchým výpočtem se lze přesvědčit, že v tomto případě není možné, aby interval (M̲̲, M̅) obsahoval správnou hodnotu M0 a zároveň některou již z nepřijatelných hodnot MD či MH.
Pokud však hodnota σ, charakterizující variabilitu výsledků chyb měření, nebude známa, musí se odhadnout z výsledků měření x1, x2, …, xn podle vzorce
,
kde = 
Interval spolehlivosti potom je
− tn − 1,α /2 . 
M̅ =
+ tn − 1,α /2 .
kde tn – 1,α /2 je tzv. 100 α /2 procentní kritická hodnota Studentova t-rozdělení s (n − 1) stupni volnosti [6]. Délka intervalu spolehlivosti
(M̅ − M̲̲) = 2 tn − 1,α /2 . samozřejmě není známa. Je závislá na hodnotě s, která bude zjištěna měřením/zkouškou. Nelze tudíž zjistit potřebný počet opakovaných měření n.
Východiskem z této situace je následující dvoustupňový postup pro určení intervalu spolehlivosti předem dané délky:
1. uskuteční se n1 opakovaných měření sledované veličiny X a následně se vypočítají základní statistické ukazatele výsledku:
výběrový aritmetický průměr
1 = 
(x1 + x2 + … + xn1)
a výběrová směrodatná odchylka
,
2. vypočte se délka intervalu spolehlivosti při těchto hodnotách
Je-li d1 ≤ Δ, postupuje se stejně jako v případě, kdy je známa σ s hodnotou s1 na místo σ.
3. Jestliže v 2. kroku vyjde d1 > Δ, provede se dalších n2 měření xn1+1, xn1+2,…,xn1+ Xn1+n2 a vypočte se nový aritmetický průměr
= 
(x1 + x2 + … + xn1 + xn1+1 + xn1+n2),
je výběrový aritmetický průměr všech n = n1 + n2 měření.
Interval spolehlivosti (M̲̲, M̅) se určí jako
− Δ, M̅ = + Δ,
Počet dodatečných potřebných měření n2 se určí tak, aby bylo 
. 
.
Závěr
O tomto století se předpovídá, že bude „Stoletím kvality“. Zlepšení kvality výrobků vyžaduje správné, přesné a nestranné zkoušení podle mezinárodně uznávaných zkušebních metod a vhodné využití statistických metod při hodnocení naměřených výsledků. V plné míře to platí mj. pro posuzování shody/certifikaci výrobků a při výzkumu a vývoji nových materiálových výrobků.
Résumé
It is predicted about the current century that it will be “The century of quality”. Without question the products΄ quality improvement demands not only the correct, accurate and fair testing according to the respected international test methods, but also the statistical methods used properly during the assessment of measured results. It is valid fully for the products conformity assessment/certification, and in the research and development of new material products.
Literatura
- [1] Zákon č. 22/1997 Sb., ze dne 24. ledna 1997 o technických požadavcích na výrobky a o změně a doplnění některých zákonů ve znění pozdějších předpisů.
- [2] Nařízení vlády č. 163/2002 Sb., ze dne 6. března 2002, kterým se stanoví technické požadavky na vybrané stavební výrobky, ve znění pozdějších předpisů.
- [3] Nařízení Evropského parlamentu a Rady (EU) č. 305/2011 ze dne 9. března 2011, kterým se stanoví harmonizované podmínky pro uvádění stavebních výrobků na trh, a kterým se zrušuje směrnice Rady 89/106/EHS, ve znění po opravě zveřejněné.
- [4] MELOUN, M., MILITKÝ, J. Statistické zpracování experimentálních dat. Praha: PLUS, 1994.
- [5] DVOŘÁK, O. Využití statistiky v požárním zkušebnictví. Sborník UCEEB ČVUT Praha. Buštěhrad: UCEEB, 2015.
- [6] JANKO, J. Statistické tabulky. Praha: Nakladatelství ČAV, 1958.
This paper proposes statistical methods for evaluation quantitative performance determinated by tests of building products for objective decision during conformity assessment / certification in a fire protection field. The procedure is applicable for other types of products, and research / development of new material products.
