Vliv stínění na výpočet pasivních solárních zisků
Parametrické studie a citlivostní analýzy, aplikované na výpočet potřeby tepla na vytápění, ukazují, že se pasivní solární zisky u dobře zateplených budov projevují jako velmi významný, ale zároveň poměrně nevyzpytatelný a obtížně definovatelný zdroj. Jde o hodnotu proměnlivou a do značné míry nespolehlivou.
1. Úvod
Parametrické studie a citlivostní analýzy (6), aplikované na výpočet potřeby tepla na vytápění, ukazují, že se pasivní solární zisky u dobře zateplených budov projevují jako velmi významný, ale zároveň poměrně nevyzpytatelný a obtížně definovatelný zdroj. Jde o hodnotu proměnlivou a do značné míry nespolehlivou.
Běžně používaný postup výpočtu podle (2) přiřazuje průsvitné konstrukci v měsíčním kroku po celý rok stejnou výslednou hodnotu korekčního činitele stínění a celkové propustnosti slunečního záření. Je otázkou, do jaké míry je toto zjednodušení vhodné pro nízkoenergetické a pasivní domy. Příspěvek se zabývá srovnáním normového a podrobnějšího způsobu výpočtu pasivních solárních zisků v situacích zastínění běžnými stavebními konstrukcemi a okolními překážkami a jejich následného vlivu na potřebu tepla na vytápění.
2. Výpočet podle ISO 13790
Standardy používané k výpočtu potřeby tepla na vytápění (2), (3) přistupují k výpočtu solárních zisků v měsíčním kroku podle stejného předpisu.
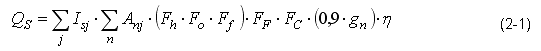
Isj - je celkové množství glob. slunečního záření na povrch n o orientaci j
Anj - je plocha otvoru hodnocené průsvitné konstrukce (okna) n o orientaci j
Fh, Fo, Ff - jsou dílčí činitele stínění horizontem, markýzou, bočními žebry
FF - je korekční činitel rámu
FC - je korekční činitel clonění
g0 - je celková propustnost slunečního záření v kolmém směru
η - využitelnost tepelných zisků
Korekční činitelé stínicích konstrukcí (Fh, Fo, Ff) jsou získávány interpolací z tabelovaných hodnot v závislosti na dané zeměpisné výšce lokality a úhlu svíraném spojnicí stínicí hrany překážky a středu okna s rovinou okna (viz (2) příloha G). Vzájemným vynásobením členů F v rovnici (2-1) lze získat výsledný korekční činitel stínění, jehož hodnota zůstává podle normového výpočetního postupu pro všechny měsíce v roce stejná. Celková propustnost slunečního záření je pro celý rok a všechny orientace dána také jedinou hodnotou, a to go sníženou na 90%.
3. Modelový výpočet
3.1. Cíle
Cílem výpočtu je podrobné vyhodnocení zastínění zadaného kolektoru (zasklení) běžnými stavebními konstrukcemi (ostění, markýza, představené svislé clony, atd.). Předmětem přesnějšího výpočtu jsou veličiny z (2-1), které se v průběhu roku vlivem způsobu výpočtu stínění mění:
- celková propustnost slunečního záření g
- celkový korekční činitel stínění F (nahrazující součin členů Fx v rovnici 2-1)
3.2. Metodika
Pro výpočet byl zvolen numericko-analytický přístup. Numerická část spočívá v rozdělení plochy kolektoru na malé jednotkové plochy reprezentované bodem v jejich těžišti. Analytický přístup je uplatněn při modelování překážek. Pro každý bod je pak prováděn výpočet individuálně.
Základními vstupními daty je globální sluneční záření dopadající na vodorovnou rovinu Io [W/m2]. Byla použita data ze softwaru Meteonorm 6.0 (4) pro průměrný rok za období 1981-1990, lokalita Praha. Podle Perezova modelu (1) je záření přepočítáváno na požadovaný sklon a orientaci. Celkové dopadající záření je pro plochu kolektoru (okna) zapsáno pomocí intenzit přímé, difúzní a sumy odražených složek záření. Se složkami slunečního záření je pracováno odděleně. Před jejich opětovnou syntézou pro daný sklon a orientaci je v každém časovém kroku, s ohledem na pozici Slunce a zadané stínicí překážky, vyčíslen příslušný korekční činitel stínění nebo pohledový faktor, jímž je daná složka vynásobena. Výpočet je prováděn v hodinovém kroku. Výsledný korekční činitel stínění F a celková tepelná propustnost záření g pro zvolené období je vždy hodnota vážená přes intenzity dopadajícího záření.
4. Porovnání sledovaných veličin
4.1. Celková propustnost solárního záření - g
Aby bylo možno zjistit, jak sluneční energie ovlivní vnitřní prostředí, je potřeba se zabývat jejím prostupem zasklením. Hodnota g je závislá na úhlu dopadu záření, což normový výpočet znesnadňuje, proto je nahrazen paušální hodnotou 0,9 go. Tvar křivky úhlové závislosti je určován především počtem okenních tabulí a povrchovou úpravou skel. Hodnota g je počítána podle (5) v každém kroku odděleně pro všechny složky záření. V následujících výpočtech bylo uvažováno trojsklo s go=0,5 a nízkoemisivní vrstvou.
Provedené parametrické studie různých případů zastínění ukázaly, že měsíční hodnoty celkové propustnosti slunečního záření jsou výrazně závislé na orientaci posuzovaného svislého okna. Charakteristické průběhy hodnot g v procentuálním úbytku z g0 (normálová hodnota) jsou naznačeny v grafu 1.
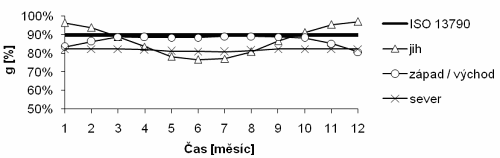
Graf. 1 Procentuální úbytek hodnoty celkové propustnosti slunečního záření pro různé orientace
Ukazuje se, že měsíční hodnoty celkové propustnosti solárního záření zasklením se v průběhu roku pohybují v intervalu 77% -96% z normálové propustnosti g0. Jižní orientace v zimních měsících norma podhodnocuje, západní a východní orientace lehce přeceňuje. Letní období je z pohledu potřeby tepla na vytápění irelevantní hodnotit.
4.2. Korekční činitel stínění
Pro porovnání korekčních činitelů stínění zjištěných normovým postupem a přesnějším výpočtem byly záměrně vybrány zcela jednoduché situace, na nichž jsou dobře pozorovatelné charakteristické odlišnosti. Dále je poukázáno jen na největší zjištěné odchylky. Výpočet byl proveden pro okno rozměrů 1000 x 1000 mm. Šířka rámu je záměrně uvažovaná jako nulová, aby neovlivňovala důsledky zvolených stínicích překážek. Vyložení markýzy a bočních žeber je určeno úhlem α podle postupu v (2).
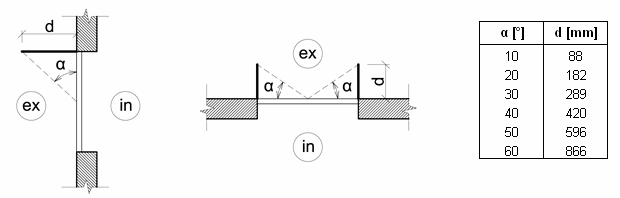
Obr. 1, 2 Schéma zadání stínicích překážek; markýza a boční žebra
Tab. 1 Délka vyložení markýzy pro zadané okno (1000x1000mm) - přepočet α na délku překážky d
1) Markýza - jižní orientace
Norma v zimních měsících udává pro jižně orientované okno s markýzou nižší korekční činitel stínění (připisuje markýze větší stínicí úlohu). Trend se zvýrazňuje s větším vyložením markýzy a zkracováním bočních přesahů. Křivky se značkou čtverce v grafu 2 a 3 ukazují průběhy F pro případ, kdy je šířka markýzy rovna šířce okna.
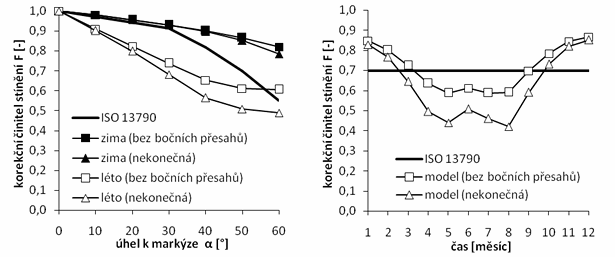
Graf. 2 Korekční činitele stínění pro normový a modelový výpočet v závislosti na vyložení markýzy
Graf. 3 Měsíční hodnoty korekčních činitelů stínění pro vyložení markýzy pod úlem α =50°
2) Boční žebra - západní orientace
Norma v tomto případě stínicí potenciál žeber značně podceňuje. Rozdíly se zvětšují s délkou žeber a jsou výraznější v zimním období, kdy jižní žebro výrazně stíní polední slunce, které navíc zapadá už na JZ. Severní žebro nestíní přímou složku, ale ubírá část difúzního záření.
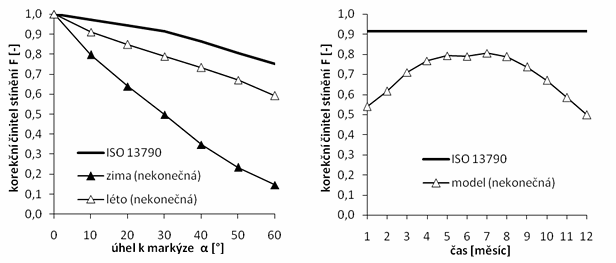
Graf. 7 Korekční činitele stínění pro normový a modelový výpočet v závislosti na vyložení markýzy
Graf. 8 Měsíční hodnoty korekčních činitelů stínění pro stínicí hranu žebra pod úlem α =30°
5. Energetické důsledky
Provedené výpočty ukázaly v některých příkladech značné odlišnosti v průbězích korekčních činitelů stínění. Celková propustnost slunečního záření vykazuje v průběhu roku větší shodu. Výslednou hodnotu solárních zisků v jednotlivých měsících ovšem určují podle rovnice (2-1) i další parametry (plocha okna a hodnota slunečního záření a jeho využitelnost), které relativní srovnání pomocí korekčních činitelů stínění převádějí do absolutních hodnot solárních zisků. Velké odlišnosti v korekčních činitelích např. v prosinci nebo při západní orientaci nemusejí být po vynásobení nízkou hodnotou záření v celoroční bilanci rozhodující, nebo naopak malý rozdíl po vynásobení větší intenzitou (např. jižní orientace v dubnu) na významu nabude. Měsíční rozdíly a jejich celoroční sumu pro prezentované případy uvádění grafy 10 a 11. Kladné ΔQs značí, že norma zisky nadhodnocuje, záporné ΔQs znamená opak.
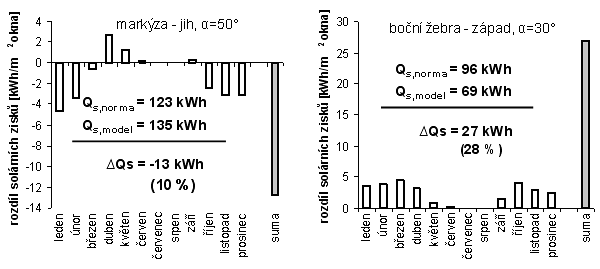
Graf. 10 resp. 11 Rozdíl měsíčních hodnot solárních zisků vypočtených normovým vs. přesnějším
modelovým postupem pro situace 1) markýza - jih resp. 2) boční žebra - západ. Ve výpočtech je
zohledněna využitelnost tepelných zisků (průměrné výpočtové hodnoty pro pasivní RD).
Zůstává otázkou, jak se rozdíl ve vypočtených solárních ziscích ΔQs, projeví v potřebě tepla na vytápění Qh. Vyjdeme-li z klasického zápisu (5-1), lze podíl ΔQs na Qh vyjádřit pomocí koeficientu k podle (5-2).
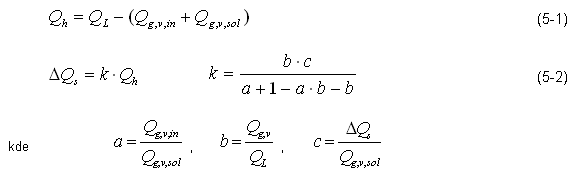
ΔQs - je rozdíl solárních zisků vzniklý metodou výpočtu
Qh - je potřeba tepla na vytápění objektu
Qg,v,in - jsou využitelné vnitřní tepelné zisky
Qg,v,sol - jsou využitelné solární zisky (podle normy)
Qg,v - jsou využitelné tepelné zisky (vnitřní + solární)
QL - je tepelná ztráta objektu (za hodnocené období, v kWh)
S rostoucím koeficientem k roste podíl nepřesnosti výpočtu solárních zisků na potřebě tepla na vytápění. Jednoduchá parametrická analýza ukazuje, že koeficient k roste, když:
- klesá a (klesá podíl vnitřních zisků vůči solárním)
- roste b (roste podíl zisků vůči tepelné ztrátě)
- roste c (roste rozdíl ve výpočtu zisků vůči hodnotě solárních zisků)
Vzhledem ke skutečnosti, že parametr c je prakticky nezávislý na kvalitě domu (Qh), je ověřen předpoklad, že u objektů s nízkou potřebou tepla na vytápění, kde významnou roli hrají solární zisky, a ve větší míře se uplatňují stínicí prvky, hraje nepřesnost výpočtu solárních zisků největší roli.
6. Závěr
Provedené výpočty ukázaly, že i při extrémních zadáních založených na prezentovaných příkladech (okna pouze na jih s markýzou, okna pouze na západ s žebry) pro objekty s potřebou tepla 15-20 kWh/m2.rok, ovlivňuje nepřesnost výpočtu pasivních solárních zisků výslednou potřebu tepla na vytápění do 10 %. Je potřeba si ovšem uvědomit, že ΔQs roste s výraznějším zastíněním, čímž se ovšem snižuje i poměr pasivních solárních zisků vůči tepelné ztrátě, a dále skutečnost, že pro různé situace se mění velikost i znaménko ΔQs. Pro mnohé případy se odchylky na jednom okně nebo v rámci objektu na různých oknech vzájemně kompenzují. Lze závěrem konstatovat, že pro většinu nízkoenergetických a pasivních bytových staveb je vliv přesnějšího výpočtu korekčních činitelů stínění pro zjištění potřeby tepla na vytápění, v řádu +/- 2-3% z Qh. Se zvyšující se měrnou potřebou tepla na vytápění tento vliv klesá. Výraznější rozdíl lze očekávat u objektů s opakujícím se stínicím schématem při stejné orientaci a velkých plochách okenních otvorů. Rozdíl také vzroste se zvyšující se intenzitou dopadajícího slunečního záření.
Indicie k uplatnění přesnějšího výpočtu vedou k budovám s velkými prosklenými plochami na fasádách (např. administrativní budovy a nemocnice). U takovýchto objektů bude ovšem hlavní potenciál přesnějšího výpočtu svázán spíše s vyhodnocením komfortu vnitřního prostředí a zabráněním přehřívání interiéru.
7. Literatura
1) DUFFIE, J.A. - BECKMAN, A. Solar Engineering of Thermal Processes. 2.vyd. New York: John Wiley & Sons, 1991, IISBN 0-471-51056-4
2) ISO 13790 (2008). Energy performance of buildings - Calculation of energy use for space heating and cooling
3) ČSN EN 832 (2000). Tepelné chování budov - Výpočet potřeby energie na vytápění - obytné budovy
4) METEONORM version 6.0, Global Meteorological Database, (2007)
5) KARLSSON, J., ROOS, A. Modelling the angular behaviour of the total solar energy transmittance of windows, Solar Energy, 2000, Volume 83, s. 321 329
6) ANTONÍN, J., KOPECKÝ, P. Tepelná bilance pasivních a nízkoenergetických rodinných domů: parametrická studie, Sborník Pasivní domy 2009
1 Výpočet korekčních činitelů stínění je ovlivněn hlavně profilem slunečního záření během roku. Lokalita a absolutní hodnoty záření nejsou, pokud nejsou mezi lokalitami významné podnebné rozdíly, rozhodující.
A commonly used procedure of calculation by (2) assigns to a transparent structure the same output value of a correction factor and total throughput screening of solar radiation on a monthly basis for the whole year. The question is to what extent this simplification is appropriate for low- energy and passive houses. The paper deals with a comparison between a nominal and detailed methods of calculating passive solar gains in situations of normal shading with normal structures and surrounding barriers, and their subsequent impact on the need for heating. The calculations have showed that even in extreme cases based on the presented examples (windows only on the Southern porch, windows just to the west with grills) for buildings with heat requirements of 15-20 kWh/m2.year, the precision of the calculations of passive solar gains are affected resulting on a higher demand for heating of up to 10%.