Faktory ovlivňující vnitřní povrchovou teplotu a kondenzaci na povrchu konstrukcí – Díl 1.
Chování skutečné konstrukce se v určitých případech odlišuje od konstrukce modelované ve výpočtovém programu. Článek pojednává o faktorech, které můžou ovlivnit vlastnosti konstrukce tak, že mají vliv na povrchovou teplotu konstrukce. Jedná se zejména o působení vlhkosti uvnitř materiálu a vzdušné vlhkosti.
1. Úvod
V současnosti se vzhledem k utěsňování obálky budovy setkáváme často s povrchovou kondenzací příp. růstem plísní na povrchu konstrukcí. Ve většině případů se dá najít problém v nesprávném užívání vnitřních prostor, ale jsou zde další, možná ne tak významné faktory, které můžou mít vliv na chování konstrukce. Projektant by při návrhu konstrukce měl uvážit také faktory, které norma neuvažuje, ale můžou ovlivnit správnou funkci konstrukce.
2. Základní pojmy
Jako první bych měl obeznámit člověka neznalého problematiky s nejdůležitějšími základními pojmy a jevy. Tyto jevy jsou v současnosti velmi aktuální a vyskytují se v mnoha článcích. Přesto si je zde dovolím pro úplnost uvést.
Vnitřní povrchová teplota konstrukce θsi vyjadřuje, jakou teplotu má povrch konstrukce za určitých okrajových podmínek. Teplota na povrchu konstrukce má výrazný vliv na vznik kondenzace příp. růst plísní na jejím povrchu. Protože se povrchová teplota konstrukce mění vzhledem k posuzovanému místu, je důležité, aby při návrhu obvodových konstrukcí bylo posouzeno nejkritičtější místo objektu (jedná se zejména o kouty styku více konstrukcí, jejich vzájemné napojení, nebo nestandardně řešené detaily). Pro toto místo dle ČSN 73 0540-2 (2011) [2] musí být dodržena podmínka:
kde
- fRsi
- – teplotní faktor vnitřního povrchu [-]
- fRsi,N
- – požadovaná hodnota nejnižšího teplotního faktoru vnitřního povrchu [-]
Při výpočtech se vyjadřuje vnitřní povrchová teplota θsi také v poměrném tvaru jako teplotní faktor vnitřního povrchu fRsi [-], nebo jako poměrný teplotní rozdíl vnitřního povrchu ξRsi:
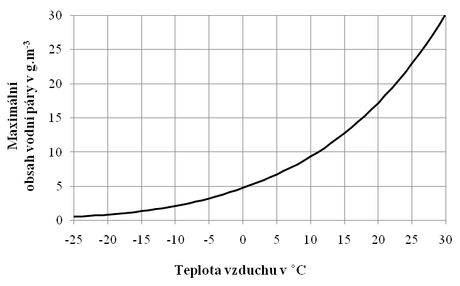
Obr. 2.1 Graf závislosti obsahu vodní páry na teplotě vzduchu
Dalším důležitým pojmem je teplota rosného bodu vzduchu. Teplota rosného bodu je teplota, při které je vzduch maximálně nasycen vodní párou. Vzduch může za dané teploty obsahovat pouze určité množství vodní páry, přičemž se stoupající teplotou může obsahovat víc vodní páry v jednotce objemu, aniž by docházelo k jejímu zkapalnění. To je důvod, proč vůbec teplota rosného bodu vzduchu existuje.
V případě poklesu teploty pod hodnotu teploty rosného bodu vzduchu dochází ke kondenzaci přebytečné vlhkosti. Pro pochopení se dá proces zjednodušit a znázornit následujícím obrázkem.
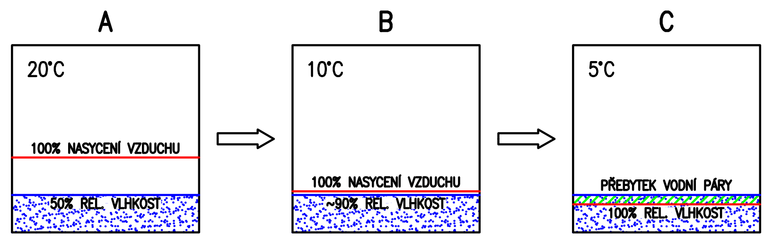
Obr. 2.2 Průběh změn teploty vzduchu vedoucí ke vzniku kondenzace vodních par
Na obr. 2.2 (A) je vidět že vzduch o teplotě 20 ˚C má určitou hranici maximálního obsahu vodních par. Tato hranice je označena červeně jako 100% nasycení vzduchu. V případě, že je ve vzduchu polovina objemu vodních par, které může vzduch o dané teplotě maximálně obsahovat, relativní vlhkost vzduchu dosahuje 50 % (hranice označena modrou čárou). Relativní vlhkost vzduchu v procentech je tedy pouhým poměrem mezi skutečným obsahem vodních par a maximálním obsahem vodních par ve vzduchu pro jeho určitou teplotu.
Když se teplota snižuje (např. na teplotu 10 ˚C), obsah vodní páry zůstává stejný, jak je vidět na obr. 2.2 (B). Změní se však hodnota maximálního nasycení vodními parami, protože chladnější vzduch dokáže udržet pouze menší množství vodních par (posun červené čáry směrem dolů). Relativní vlhkost se proto jako poměr zvýší. Tady lze vidět, že při uvedeném poklesu z 20 ˚C na teplotu 10 ˚C zůstává obsah vodní páry stejný, ale relativní vlhkost se jako poměr zvýší na přibližně 90 %.
Při poklesu teploty pod hodnotu rosného bodu, nastává situace, kdy hranice maximálního nasycení vodní párou poklesne pod skutečné nasycení vzduchu vodní parou (obr. 2.2 (C)). Relativní vlhkost ale nemůže být větší než 100 %, proto vlhkost zůstane na této hranici a přebytečná vlhkost (označena zeleně) zkondenzuje.
3. Problémy spojené se zvýšenou vlhkostí
Problémy jako zvýšená vlhkost případně růst plísní na povrchu konstrukcí se vyskytují zejména v oblastech kritických detailů, kde je povrchová teplota konstrukce výrazně nižší než v souvislých plochách. Jedná se zejména o kouty a rohy, případně přechody různých druhů konstrukcí.
Tím, že je teplota povrchu nižší, než teplota interiéru dochází k jevu popsanému v předchozí kapitole. Ve stručnosti se vzduch v blízkosti povrchu konstrukce ochlazuje a tím zvyšuje svojí relativní vlhkost. V případě, že relativní vlhkost dosahuje hranice 100 %, tak při dalším poklesu teploty dochází ke kondenzaci na povrchu, kde je teplota pod hodnotou teploty rosného bodu. Důsledkem tohoto jevu jsou vlhkostní mapy vzniklé na povrchu konstrukcí, které můžou mít v dlouhodobém hledisku nepříznivé dopady.
Ke vzniku plísní na povrchu konstrukcí, nemusí docházet pouze po vzniku vlhkých oblastí. Plísním stačí zvýšená vlhkost vzduchu, pohybující se nad hodnotou 80 %. V současnosti se konstrukce podle norem posuzují právě na tuto hodnotu, čímž se při splnění daných parametrů vnitřního prostředí zamezuje uvedenému růstu plísní a zároveň kondenzace na povrchu konstrukcí.
4. Vlivy, které můžou způsobit růst plísní příp. povrchovou kondenzaci
Konstrukce v některých případech neodpovídají ve skutečnosti modelu, za pomoci kterého byla konstrukce navržena. Jako příklad uvádím měření, kde povrchová teplota koutu byla důvodem k povrchové kondenzaci vodních par. Rozdíl reálného chování konstrukce a modelu byl výrazný. Výsledky měření a řešení 2D teplotního pole koutu konstrukcí jsou uvedena v následující tabulce. Obě konstrukce při posouzení vyhovovaly požadavkům normy na nejnižší vnitřní povrchovou teplotu.
| θai [˚C] | θsi [˚C] 2D teplotní pole θe = −8 ˚C | θsi [˚C] termogramy θe = −8 ˚C | Δθsi [˚C] | |
|---|---|---|---|---|
| Kout, skladba S1 (Porotherm 44 P+D) | 22 | 16,8 | 11,4 | 5,4 |
| Kout, skladba S2 (Železobet. věnec) | 22 | 15,6 | 8,6 | 7,0 |
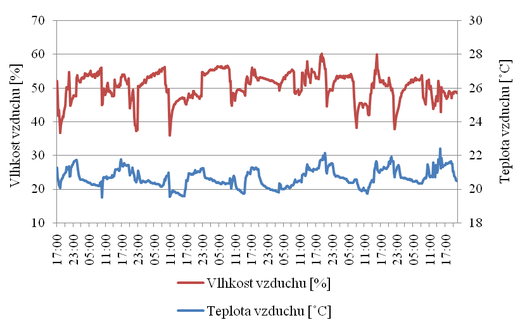
Obr. 4.1 Ukázka změn tepelně vlhkostních parametrů v průběhu několika dnů v reálné pobytové místnosti
Povrchová kondenzace a růst plísní jsou často způsobeny nesprávným užíváním vnitřních prostor. Je to způsobeno zejména používáním mnohem vzduchotěsnějších výrobků (zejména oken), která svojí těsností neumožňují přirozenou infiltraci vzduchu. Proto je nemožné neřízeným větráním dodržovat parametry vnitřního prostředí přirozeným způsobem na konstantních hodnotách nebo hodnotách velmi blízkých těm, na které byla konstrukce navržena. V reálném prostředí dochází k výrazným výchylkám v teplotách a vlhkostech, kterou by však měla pokrýt bezpečnostní přirážka normy. Někdy tomu tak není a tehdy může docházet k povrchové kondenzaci vlivem nesprávného užívání vnitřních prostor.
Další možností je lišící se povrchová teplota konstrukce od navrhovaného stavu. Skutečná vnitřní povrchová teplota konstrukcí se v některých případech může lišit od teploty, která byla modelována ve výpočtových programech. Je zde několik faktorů, které nejsou v současnosti při posuzování konstrukcí uvažovány a můžou mít vliv na povrchovou teplotu konstrukce. K výraznějšímu rozdílu může docházet zejména jejich kombinací. Rozdíl v teplotách reálné a modelované konstrukce může být tedy způsoben např.:
- rozdílným nebo nepřesným skutečným provedením konstrukcí (změna materiálu nebo jeho tloušťky, skrytý tepelný most apod.),
- vlivem změny tepelné vodivosti způsobené zvýšenou vlhkostí materiálu,
- hromaděním kondenzátu uvnitř konstrukce,
- jiné vnější vlivy jako nevhodně řešená tepelná vazba apod.,
- kombinací vlivů, kdy jeden je důsledkem dalšího.
V dalších částech se budu zabývat zhodnocením vlivu některých faktorů na povrchovou teplotu konstrukce příp. povrchovou kondenzaci. Jedná se o zhodnocení vlivu vlhkosti materiálu na povrchovou teplotu, rozdíly v oblastech kondenzace uvnitř konstrukce u dutinových tvarovek při různém pojetí idealizace modelu a vlivem parametrů vnitřního prostředí na vznik kondenzačních oblastí.
5. Zhodnocení vlivu vlhkosti materiálu na povrchovou teplotu
Způsobů, kterými se může do konstrukce dostat voda je několik. Mezi nejvýznamnější patří mimo jiné kondenzace při difúzi vodních par, vzlínání vlhkosti a navlhání konstrukce povrchovou kondenzací.
Pokud ke kondenzaci vodních par dochází, jedná se ve většině případů o kondenzaci v zimním období. Kondenzát se však ve správně navržené konstrukci v průběhu několika let nehromadí, protože se v letním období nahromaděná vlhkost odpaří.
Vlhkost uvnitř konstrukce však může zhoršovat izolační vlastnosti materiálu. Z uvedeného plyne, že ke zhoršování izolačních vlastností může docházet v zimním období, kdy se vlivem zhoršených izolačních parametrů mohou vyskytnout problémy, které se s materiálem bez vlhkosti nemusí objevit.
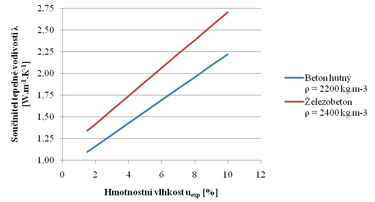
Závislost hmotnostní vlhkosti a součinitele tepelné vodivosti lze vyjádřit pomocí ČSN 73 0540-3 [3]. Jako vstupní hodnoty pro výpočet skutečné tepelné vodivosti je potřeba znát hodnoty charakteristické a okamžité hmotnostní vlhkosti, vlhkostní součinitel materiálu a charakteristickou hodnotu součinitele tepelné vodivosti. Výpočet nelze jednoduše provést pro materiály, kde může vznikat několik způsobů šíření a hromadění vlhkosti. V následujících grafech jsou uvedeny příklady závislosti pro vybrané druhy homogenních izolačních a konstrukčních materiálů.
Z uvedených grafů (obr. 5.1 a obr. 5.2) je zřejmé, že vlhkost materiálu může mít výrazně nepříznivý vliv na hodnotu součinitele tepelné vodivosti.
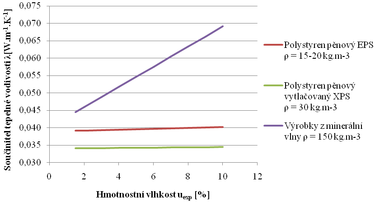
Obr. 5.1 Závislost součinitele tepelné vodivosti na hmotnostní vlhkosti vybraných izolačních materiálů
5.1. Geometrie a vstupní data modelu
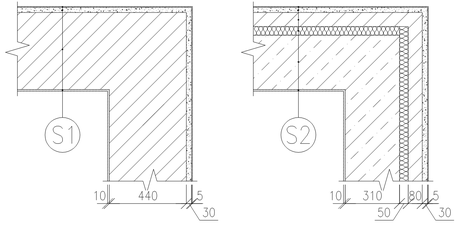
Obr. 5.3 Vybrané skladby konstrukcí
Pro zhodnocení vlivu vlhkosti na povrchovou teplotu bude pro zjednodušení uvažováno zdivo z dutinových cihelných bloků Therm jako idealizovaný materiál. V druhém případě se jedná o železobetonový věnec, který je zateplen a opatřen věncovkou. V obou případech bude výpočet proveden pro kout styku konstrukcí.
Hmotnostní vlhkost zdiva a betonu bude uvažována pouze v nejmasivnější vrstvě konstrukce a bude konstantní v celé jeho tloušťce. U věnce bude zanedbán vliv vlhkosti v zateplení vzhledem k výrazně podobným izolačním vlastnostem v uvažovaných hodnotách hmotnostních vlhkostí. Uváděná vlhkost může být do konstrukce dodávána kondenzací uvnitř konstrukce, povrchovou kondenzací příp. hromaděním v průběhu let při nedokonale navržené konstrukci.
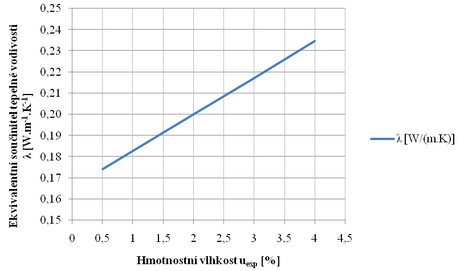
Obr. 5.4 Závislost ekvivalentního součinitele tepelné vodivosti na hmotnostní vlhkosti pro pálené zdící prvky 44 P+D; ložná spára – malta MVC 011 – 4× přerušené maltování podle ([4];kap.13.3.2)
Hodnota ekvivalentního součinitele prostupu tepla bude určena vzhledem ke komplexnosti šíření tepla v dutinových materiálech podle ([4];kap.13.3.2). Ze skladeb, které byly dlouhodobě experimentálně sledovány, byla vybrána skladba nejvíce podobná zkoumané skladbě. Jedná se o pálený zdící prvek 44 P+D; (245/440/238); ložná spára – malta MVC 011 – 4× přerušené maltování; oba povrchy opatřeny omítkou MVC 072 v tl. 10–15 mm s objemovou hmotností 865 kg/m3. Výsledky byly statisticky vyhodnoceny metodou regresní analýzy ekvivalentního součinitele tepelné vodivosti v závislosti na vlhkosti. Výsledky jsou uvedeny pro zdivo bez omítek.
Za předpokladu lineárního chování závislosti mimo oblast grafu bude hodnota pro hmotnostní vlhkost mimo hranice grafu dopočtena.
| uexp [%] | 0,5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| λu [W.m−1.K−1] | 0,17 | 0,18 | 0,20 | 0,21 | 0,23 | 0,25 | 0,26 | 0,28 | 0,30 | 0,32 | 0,33 |
Pro železobeton byla hodnota součinitele tepelné vodivosti stanovena podle vztahu a hodnot dle ČSN 73 0540-3 [3].
| uexp [%] | 1,5 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| λu [W.m−1.K−1] | 1,34 | 1,42 | 1,58 | 1,74 | 1,90 | 2,06 | 2,22 | 2,39 | 2,55 | 2,71 |
| Vrstva | d [m] | λu [W.m−1.K−1] | μ [-] | ρ [kg.m−3] |
|---|---|---|---|---|
| Vápenocementová omítka | 0,005 | 0,8 | 14 | 1450 |
| Tepelněizolační omítka | 0,03 | 0,13 | 8 | 400 |
| Keramické zdivo Therm 44 P+D | 0,44 | - | 7 | 800 |
| Vápenocementová omítka | 0,01 | 0,8 | 14 | 1450 |
| Vrstva | d [m] | λu [W.m−1.K−1] | μ [-] | ρ [kg.m−3] |
|---|---|---|---|---|
| Vápenocementová omítka | 0,005 | 0,8 | 14 | 1450 |
| Tepelněizolační omítka | 0,03 | 0,13 | 8 | 400 |
| Keramické věncovky | 0,08 | 0,3 | 7 | 800 |
| Pěnový polystyren EPS 70F | 0,05 | 0,044 | 21 | 15 |
| Železobetonový věnec | 0,31 | - | 29 | 2400 |
| Vápenocementová omítka | 0,01 | 0,8 | 14 | 1450 |
5.2. Řešení a výsledky dvourozměrného stacionárního pole teplot
Výchozí okrajové podmínky byly voleny následovně:
| teplota vnitřního vzduchu | θai = 20 ˚C |
| teplota venkovního vzduchu | θe = −15 ˚C |
| odpor při přestupu tepla na vnitřní straně konstrukce | Rsi = 0,25 m2.K.W−1 |
| odpor při přestupu tepla na vnější straně konstrukce | Rse = 0,04 m2.K.W−1 |
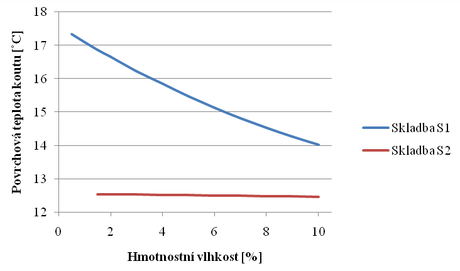
Obr. 5.5 Závislost povrchové teploty na hmotnostní vlhkosti obsažené v nejhmotnější vrstvě konstrukce
Pole teplot bylo řešeno v programu Area 2009 firmy Svoboda software.
Generování sítě bylo provedeno automaticky v grafickém editoru s maximálním počtem neznámých 5000. Síť byla v případě detailu železobetonového věnce kvůli nízkému rozdílu mezi variantami pro zpřesnění zhuštěna v blízkosti vnitřního povrchu v rozhraní číselného vstupu dat v programu Area.
Výsledky řešení jsou kvůli komplexnosti šíření vlhkosti v konstrukcích a značná zjednodušení pouze orientační a u každé konstrukce se můžou projevit v jiné míře.
5.3. Závěr
Výpočet a vlhkostní chování konstrukce bylo značně zjednodušeno a hmotnostní vlhkost se může v různých konstrukcích objevovat v různé míře. Rozložení vlhkosti v konstrukci často není rovnoměrné, a proto jsou uvedené výsledky pouze orientační.
Rozdíl povrchových teplot u zděné konstrukce s vlivem zvýšené vlhkosti materiálu mění docela výrazně podle obsažené vlhkosti.
U konstrukce železobetonového věnce se hodnota povrchové teploty mění velmi mírně. Zde však přebírá největší teplotní rozdíl zateplení polystyrenem. Vliv zvýšené vlhkosti v polystyrenu v uvedených mezích hmotnostní vlhkosti nebyl uvažován.
Jako příklad zde mohu uvést reálné měření, ve kterém byla naměřena hmotnostní vlhkost materiálu v oblasti koutu uvedených skladeb kolem 9 %. Vlhkost byla měřena povrchovou sondou, která umožňuje měření do hloubky přibližně 30 mm. Hmotnostní vlhkost zdiva a betonu bude uvažována průměrnou hodnotou z provedeného povrchového měření experimentálního objektu tj. uexp = 9 % a bude konstantní v celé jeho tloušťce. Aby byla hodnota v celé tloušťce konstantní, je předpokládáno, že hmotnostní vlhkost je uvnitř konstrukce z části tvořena také kondenzaci při difuzi vodních par. V následující tabulce je vidět rozdíl povrchových teplot koutů při charakteristických vlhkostech materiálu a při uvažované vlhkosti v nejhmotnější vrstvě konstrukce.
| θai [˚C] | Δθsi [˚C] | θe [˚C] | ΔfRsi [-] | Rsi [m2.K.W−1] | Rse [m2.K.W−1] | |
|---|---|---|---|---|---|---|
| Kout, skladba (Therm 44 P+D) | 20 | 2,73 | −15 | 0,078 | 0,25 | 0,04 |
| 22 | 2,89 | |||||
| 24 | 3,04 | |||||
| Kout, skladba (Železobet. věnec) | 20 | 0,07 | 0,002 | |||
| 22 | 0,07 | |||||
| 24 | 0,08 |
V další části článku porovnáme kondenzační oblasti detailu při modelovaní ve výpočtovém programu u idealizovaného detailu a detailu modelovaného podle skutečného materiálového složení a uvedeme příklady tepelně vlhkostního chování reálných vnitřních prostor.
6. Poděkování
Tento článek vznikl za podpory projektu specifického výzkumu FAST-S-11-64/1435 na Fakultě stavební VUT v Brně.
7. Použitá literatura
- [1] PAPRANEC, Michal. Vliv parametrů vnitřního prostředí na vznik kondenzačních oblastí. Brno, 2011. 77 s., Diplomová práce. Vysoké učení technické v Brně, Fakulta stavební, Ústav pozemního stavitelství.
- [2] ČSN 73 0540-2. Tepellná ochrana budov: Část 2: Požadavky. Praha: Český normalizační institut, 2011. 53 s.
- [3] ČSN 73 0540-3. Tepelná ochrana budov: Část 3: Návrhové hodnoty veličin. Praha: Český normalizační institut, 2005. 95 s.
- [4] Cihlářský lexikon [online]. Česká republika, leden 2007 [cit. 2011-11-29]. Dostupné z WWW:
http://www.cscm.cz/lexikon/lexikonkpl.pdf. - [5] ČSN EN ISO 13788 (73 0544). Tepelně vlhkostní chování stavebních dílců a stavebních prvků: Vnitřní povrchová teplota pro vyloučení kritické povrchové vlhkosti a kondenzace uvnitř konstrukce – Výpočtové metody. Praha: Český normalizační institut, 2002. 38 s.
The behaviour of real structures in some cases differs from the structure modeled in computational program. Article deals with the influences that can affect the characteristics of the structure, so that they affect the surface temperature of the structure. In particular, the moisture inside the material and air humidity.