K prostupu tepla reflexními tepelnými izolacemi
Na trhu s tepelně izolačními materiály lze koupit mimo obvyklé izolační výrobky i tzv. reflexní tepelné izolace. Může se například jednat o kombinaci plastové fólie s uzavřenými vzduchovými polštářky s několika vrstvami pokovené fólie. Prodejci reflexních izolací často tvrdí, že součinitel tepelné vodivosti reflexní tepelné izolace dosahuje hodnot nižších než 0,01 W/(m‧K). Jeden prodejce sděluje tuto skutečnost spotřebiteli jinou formou: tři centimetry reflexní tepelné izolace se vyrovnají dvaceti centimetrům minerální vlny. Jsou ale takové vlastnosti vůbec fyzikálně možné?
Úvod
Tepelněizolační materiály jsou soustavou velmi malých pórů a skeletu. V materiálu dochází ke třem mechanismům přenosu tepla: k vedení, proudění a sálání. Vedení probíhá v pevné fázi. Vedení a proudění probíhá v pórech tepelné izolace, v kterých je uzavřený nějaký plyn, nejčastěji vzduch. Molekuly plynu se pohybují a tím přenášejí teplo. Přenos tepla sáláním je přenos energie mezi dvěma tělesy o různé teplotě šířením elektromagnetických vln. V rámci tepelné izolace jde o dlouhovlnné záření z jedné stěny póru na stěnu druhou.
V inženýrské praxi se přenos tepla přes tepelnou izolaci modeluje jako vedení tepla. Schopnost materiálu zabraňovat přenosu tepla je charakterizována hodnotou součinitele tepelné vodivosti. Ten lze změřit jednoduchými metodami založenými na vytvoření ustáleného teplotního rozdílu. Součinitel tepelné vodivosti jakéhokoliv materiálu závisí na teplotě, vlhkosti a objemové hmotnosti.
Výpočet součinitele tepelné vodivosti reflexní tepelné izolace
Teorie
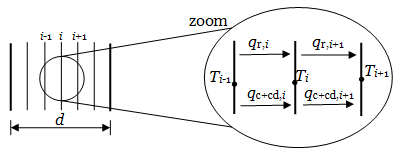
Obrázek 1:
Vlevo – reflexní tepelná izolace tvořená několika rovnoběžnými fóliemi.
Vpravo – přenos tepla ve dvou uzavřených vzduchových dutinách.
Pro účely výpočtu součinitele tepelné vodivosti si lze reflexní tepelnou izolaci zjednodušeně představit jako soustavu několika rovnoběžných fólií řazených za sebou (obrázek 1, vlevo). Oba povrchy fólie mají nízkou emisivitu. Mezi jednotlivými fóliemi jsou vytvořeny tenké uzavřené vzduchové vrstvy.
Schéma na obrázku 1, vpravo zobrazuje dva paralelní tepelné toky. První z nich představuje proudění a vedení ve vrstvě vzduchu mezi fóliemi (index c+cd). Druhý z nich představuje sálání z jednoho povrchu na povrch druhý (index r).
Tepelná bilance i-tého uzlu:
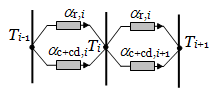
Obrázek 2: Grafické schéma modelu přenosu tepla ve dvou uzavřených vzduchových dutinách (analogie s elektrickým obvodem).
Hustotu tepelného toku lze vyjádřit jako součin součinitele přestupu tepla a rozdílu teplot (viz obrázek 2):
kde αc+cd je součinitel přestupu tepla vedením a prouděním, αr je součinitel přestupu tepla sáláním. V předchozí rovnici se zjednodušeně předpokládá, že fólie jsou tak tenké, že je možné je nahradit jedinou teplotou.
Součinitel přestupu tepla vedením a prouděním ve vzduchové dutině se vypočítá z:
kde λa je tepelná vodivost klidného vzduchu (0,024 W/(m‧K) pro 10 °C), D je tloušťka vzduchové vrstvy (m) a Nu je Nusseltovo číslo, které vyjadřuje poměr mezi tepelným tokem vyvolaným prouděním a tepelným tokem bez vlivu proudění (pouze vedení). Vztahy pro Nu je možné nalézt v literatuře pro definované geometrické konfigurace a omezující podmínky platnosti. Nicméně pokud je vrstva vzduchu dostatečně tenká (< 2 cm), tak proudění vzduchu je nízké a Nusseltovo číslo se blíží jedné, viz [1].
Sálání mezi dvěma velikými rovnoběžnými plochami představuje základní geometrický případ, který popisuje jakákoliv kniha o přenosu tepla. Pro hustotu tepelného toku sáláním mezi dvěma velikými rovnoběžnými plochami platí:
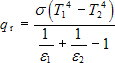 (4)
(4)
kde σ je Stefanova-Boltzmanova konstanta (5,67∙10−8 W/(m2‧K4)), ε1 je emisivita první plochy, ε2 je emisivita druhé plochy, T1 je absolutní teplota první plochy a T2 je absolutní teplota druhé plochy. Z rovnice (4) vyplývá, že emisivita obou povrchů hraje významnou roli. Rovnici (4) je možné zapsat i ve tvaru:
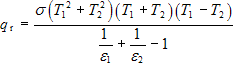 (5)
(5)
Součinitel přestupu tepla sáláním tedy je:
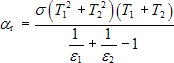 (6)
(6)
Z rovnice (6) je zřejmé, že součinitel přestupu tepla sáláním je nelineárně závislý na hodnotách absolutních teplot obou ploch. Pro blízké hodnoty obou teplot lze vztah (6) přibližně zapsat jako:
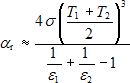 (7)
(7)
Pro účely inženýrských výpočtů obvykle stačí odhadnout hodnotu průměrné absolutní teploty (T1 + T2)/2 a tedy počítat s konstantní hodnotou součinitele přestupu tepla sáláním. Pro případ tepelné izolace můžeme odhadnout, že střední teplota leží někde mezi 20 °C a −15 °C (293 + 258)/2 = 276 K. Dosadíme-li tuto hodnotu do vztahu (7), tak dostaneme následující hodnoty, viz tabulku 1.
| (T1 + T2)/2 [K] | αr [W/(m2K)] | ||
|---|---|---|---|
| ε1 = ε2 = 0,9 | ε1 = 0,9 ε2 = 0,05 | ε1 = ε2 = 0,05 | |
| 276 | 3,89 | 0,236 | 0,122 |
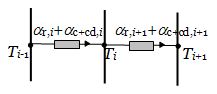
Obrázek 3: Ekvivalentní model přenosu tepla ve dvou uzavřených vzduchových dutinách.
Dvě vodivosti řazené paralelně (αc+cd a αr) můžeme sečíst do jediné hodnoty (αc+cd + αr), což je na první pohled zřejmé z algebraické úpravy rovnice (2). Graficky je tato úprava zobrazena na obrázku 3.
Výsledný tepelný odpor celé vrstvy tepelné izolace je daný součtem dílčích tepelných odporů jednotlivých vrstev:
kde N je celkový počet vrstev mezi fóliemi a Ri je tepelný odpor i-té vrstvy:
Součinitel tepelné vodivosti reflexní izolace λ [W/(m‧K)] se posléze dopočte ze vzorce:
kde d je tloušťka tepelné izolace.
Příklad
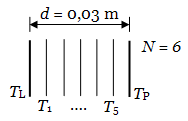
Obrázek 4: Sedm rovnoběžných pokovených fólií.
Vypočítejme tepelný odpor tepelné izolace vytvořené ze sedmi rovnoběžných fólií. Mezi jednotlivými fóliemi je vzduchová mezera 5 mm. Celková tloušťka tepelné izolace tedy je 3 cm. Emisivita obou povrchů fólie je ε = 0,05. Teplota fólie na levé straně je TL = 20 °C (293 K). Teplota fólie na pravé straně je TP = −15 °C (258 K). Součinitel tepelné vodivosti klidného vzduchu se předpokládá konstantní hodnotou 0,024 W/(m‧K).
Výsledky výpočtu shrnuje tabulka 2.
| Veličina | Označení | Hodnota | Rovnice |
|---|---|---|---|
| Součinitel přestupu tepla vedením a prouděním | αc+cd | 4,8 W/(m2K) | (3) |
| Součinitel přestupu tepla sáláním | αr | 0,12 W/(m2K) | (7) |
| Celkový tepelný odpor reflexní tepelné izolace | R | 1,22 m2K/W | (8) |
| Součinitel tepelné vodivosti reflexní tepelné izolace | λ | 0,0246 W/(m‧K) | (10) |
V předchozím výpočtu byl součinitel přestupu tepla sáláním uvažován konstantní hodnotou (lineární model). Zbývá proto zkontrolovat, zda toto zjednodušení nevede k příliš velké chybě. Výpočet byl proto provedený i pro proměnlivou hodnotu součinitele přestupu tepla sáláním (nelineární model), vypočítávanou podle rovnice (6) z hodnot absolutních teplot na rozhraních jednotlivých vzduchových vrstev.
Z porovnání výsledků jednotlivých modelů (viz tabulku 3) je zřejmé, že výpočet s konstantní hodnotou součinitele přestupu tepla sáláním je přiměřené zjednodušení. Z výsledků je dále zřejmé, že použití fólií s nízkou emisivitou značně omezuje přenos tepla sáláním. Přenos tepla vedením a prouděním vzduchu v mezeře mezi fóliemi v daném případě tvoří přibližně 98 % z celkového tepelného toku. Je proto logické, že výsledný součinitel tepelné vodivosti se blíží součiniteli tepelné vodivosti samotného vzduchu (viz tabulku 2).
| Veličina | Označení | Vrstva | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| Lineární model | Součinitel přestupu tepla sáláním | αr | 0,122 | 0,122 | 0,122 | 0,122 | 0,122 | 0,122 |
| Hustota tepelného toku sáláním | qr | 0,711 | 0,711 | 0,711 | 0,711 | 0,711 | 0,711 | |
| Hustota tepelného toku vedením a prouděním | qc+cd | 28,0 | 28,0 | 28,0 | 28,0 | 28,0 | 28,0 | |
| Nelineární model | Součinitel přestupu tepla sáláním | αr | 0,142 | 0,134 | 0,126 | 0,118 | 0,111 | 0,104 |
| Hustota tepelného toku sáláním | qr | 0,826 | 0,779 | 0,733 | 0,689 | 0,647 | 0,606 | |
| Hustota tepelného toku vedením a prouděním | qc+cd | 27,89 | 27,93 | 27,98 | 28,02 | 28,07 | 28,11 | |
Výpočet součinitele prostupu tepla stěny s reflexní tepelnou izolací
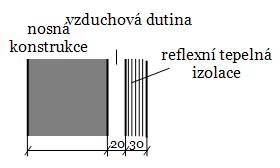
Obrázek 5: Zateplení konstrukce reflexní tepelnou izolací s uzavřenou vzduchovou dutinou.
Pro zateplení obvodového pláště budov se doporučuje vytvořit uzavřenou vzduchovou dutinu mezi nosnou konstrukcí stěny a reflexní tepelnou izolací. Příklad takové skladby je zobrazen na obrázku 5.
Dodatečná vzduchová dutina zvyšuje tepelný odpor souvrství. Jedná se o dutinu, kdy na jedné straně je povrch s vysokou emisivitou (povrch zdiva) a na druhé povrch s nízkou emisivitou (reflexní tepelná izolace). Součinitel přestupu tepla sáláním v takové dutině je přibližně 0,24 W/(m2K), viz tabulku 1. Pokud i v této dutině zanedbáme přídavný vliv proudění (což nemusí být vždy korektní), tak součinitel přestupu tepla prouděním a vedením přes dutinu o tloušťce 2 cm je 0,024 W/(m‧K)/0,02 m = 1,2 W/(m2K). Celkový tepelný odpor vzduchové dutiny je: 1/(0,24 + 1,2) = 0,69 m2K/W. V praxi je velmi těžké vytvořit dokonale uzavřenou tenkou vzduchovou dutinu. Pokud by vliv proudění nebyl zanedbatelný, tak by výsledný tepelný odpor vzduchové dutiny byl nižší.
Celkový tepelný odpor vzduchové dutiny a reflexní tepelné izolace je: 0,69 + 1,22 = 1,91 m2K/W. Dva centimetry uzavřené vzduchové dutiny a tři centimetry reflexní tepelné izolace tedy přibližně v takovém případě odpovídají osmi centimetrům minerální vlny se součinitelem tepelné vodivosti 0,04 W/(m‧K).
Podle normy [2] je požadovaná hodnota součinitele prostupu tepla pro vnější stěnu rovna 0,3 W/(m2K), což odpovídá tepelnému odporu 3,33 m2K/W. I při započtení tepelného odporu nosné konstrukce a odporů při přestupu tepla na vnitřní a vnější straně stěny pravděpodobně nedojde ke splnění požadované hodnoty součinitele prostupu tepla, natož hodnot výrazně nižších.
Závěr
Norma [3] uvádí postupy pro využití stávajících normalizovaných zkušebních metod ke stanovení deklarovaných tepelných vlastností izolačních výrobků s reflexním nebo nízkoemisním povrchem. Zodpovědný výrobce reflexní tepelné izolace by ji měl nechat otestovat v souladu s postupy uvedenými v [3].
Z fyzikálního rozboru provedeného v tomto článku vyplývá, že reflexní tepelná izolace se vzduchem uzavřeným mezi fóliemi nemůže dosahovat lepších hodnot, než je součinitel tepelné vodivosti samotného vzduchu (≈ 0,024 W/(m‧K)). K dosažení stejné tepelněizolační kvality je tedy potřeba přibližně o třetinu nižší tloušťka reflexní tepelné izolace než u běžné tepelné izolace.
Pro další zlepšení by bylo potřeba trvale uzavřít do dutiny mezi fóliemi plyn, který dosahuje nižšího součinitele tepelné vodivosti než vzduch. Ještě lepší by bylo vytvořit vakuum. Na trhu již existují vakuové tepelné izolace, viz [4], jejichž součinitel tepelné vodivosti se pohybuje pod 0,008 W/(m‧K).
Literatura
- [1] Hagentoft, C., E., Introduction to Building Physics, Studentliterattur, 2001.
- [2] ČSN 730540-2 Tepelná ochrana budov – Část 2: Požadavky, UNMZ, říjen 2011.
- [3] ČSN EN 16012 Tepelné izolace budov – Reflexní izolační výrobky – Stanovení deklarovaných tepelných vlastností, UNMZ, srpen 2012.
- [4] http://www.ecbcs.org/annexes/annex39.htm
Today, besides standard insulation products reflective thermal insulations can be purchased on the market. This may for example be a combination of closed air layers with several layers of metallized foil. Dealers of reflective insulation often claim that the thermal conductivity of reflective insulation reaches values lower than 0,01 W/(m‧K). One dealer introduces this fact to consumers in another form: three centimeters of reflective insulation are equal to twenty centimeters of mineral wool. However, are such properties physically possible?