Porovnání simulací konstrukcí s vysokou tepelněakumulační schopností

Úvod

V době, kdy se stále častěji v praxi setkáváme s používáním softwarů umožňujících modelování a hodnocení vnitřního prostředí budov či konstrukcí, je nasnadě zaměřit se na přesnější výpočty zahrnující dynamické simulace. Ty jsou vhodné jak pro přesnější zachycení energetických náročností stavebních objektů, tak pro přesnější rozložení teplotních polí obvodových konstrukcí za dynamicky se měnících okrajových podmínek.

Většina výpočtů opírajících se v současnosti o normativní postupy pro posouzení vnitřních povrchových teplot (kritického teplotního faktoru vnitřního povrchu) vychází z předpokladu ustáleného teplotního stavu [1]. Tento předpoklad je důležitý pro zjednodušení výpočtu, tak aby bylo možné výsledky získat za pomocí základních znalostí a bez nutnosti použití výpočetní techniky. Tato zjednodušení dávají bezpečný odhad chování navrhované konstrukce. Pokud ale požadujeme přesné informace o tom, jak se v závislosti na čase a změnách okrajových podmínek mění rozložení teplot v konstrukci, je nutné přistoupit k podrobnější analýze, která již použití výpočetního softwaru vyžaduje.

Protože jsme se v minulosti zaměřili na chování balkónových konstrukcí, provedeme porovnání stacionárních a nestacionárních jevů právě na těchto modelech. Vhodnost porovnání těchto konstrukcí spočívá především v jejich materiálovém složení. Protože jsou tyto konstrukce většinou z železobetonu a jsou tak velmi hmotné, je možné předpokládat, že v průběhu času bude vlivem vysoké tepelně akumulační schopnosti docházet k značnému zpoždění změn vnitřních povrchových teplot vlivem měnících se venkovních okrajových podmínek [2]. U jiných konstrukcí, např. na bázi dřeva, které se v současnosti velmi rozšiřují, je možné současná zjednodušení i nadále provádět z důvodu nižších tepelně akumulačních schopností.

Velikost akumulovaného citelného tepla nejčastěji používanými stavebními materiály závisí na jejich hmotnosti, měrné tepelné kapacitě a rozdílu teplot, při kterém dochází k akumulaci. Rychlost akumulace a vybíjení tepla je pak závislá zejména na součiniteli tepelné vodivosti tepelně akumulačního materiálu. Podstatné také je, zda je stavební materiál nebo konstrukce v přímém kontaktu s interiérem místnosti, nebo zda je mezi ní a interiérem překážka, např. ve formě nábytku nebo jiného vybavení.

Teplo však lze akumulovat také při změnách skupenství prostřednictvím tzv. PCMs (Phase Change Materials). Tyto materiály využívají pro akumulaci latentní teplo vratných skupenských změn. Aplikace PCMs zvýší tepelně akumulační kapacitu pro pasivní solární vytápění a umožní zapojení chlazení nočním větráním a časový posun pro použití strojního chlazení [3]. Mezi nejznámější způsoby integrace PCMs ve stavebních konstrukcích lze uvést následující principy:

• impregnace stavebních materiálů;
• mikro kapsle rozptýlené ve stavebním materiálu nebo prvku;
• makro zapouzdření;
• tvarově stabilizované PCMs.

Tepelně akumulační vlastnosti PCMs tedy výrazně ovlivňují i simulace stacionárního i nestacionárního teplotního pole.

Materiál a metodika

Ze základních fyzikálních dějů a vlastností konstrukcí je zřejmé, že akumulace tepla je výrazným činitelem při ovlivňování závislostí mezi povrchovými teplotami chladné a teplé strany konstrukce. Porovnání bylo rozděleno na tři hlavní části. První z nich je porovnání výpočtového modelu s reálným měřením prováděným na modelu v laboratořích na FAST VUT v Brně. Druhým tématem je vyhodnocení reálných měření prováděných na objektu na ulici Čeňka Růžičky v Brně. Ve třetím pak bylo využito naměřených klimatických dat a byly provedeny počítačové simulace. Jelikož měření na reálném modelu sloužila z velké části pro ověření možností převedení reálného modelu do počítačového prostředí, bylo důležité zjistit, jaké je při této transformaci možné očekávat rozdíly oproti reálné situaci.

Pro námi použité simulace byl použit software ANSYS Workbench 12.1. [4]. Výpočty byly porovnány s reálnými naměřenými hodnotami a s klimatickými daty z vlastních měření na reálném objektu a s daty z Lesnické Mendlovy univerzity.

Model, na kterém byla porovnání provedena, vycházel ze standardních požadavků stavební tepelné techniky na součinitel prostupu tepla a lineární činitel prostupu tepla. Jednalo se o jednovrstvé zdivo z keramických tvarovek a ISO-nosník Bronze MQ 8/8. Vytápění v prostorech vytvářející vnitřní okrajovou podmínku pro simulace na našem modelu bylo řešeno otopnými tělesy s uvažovanou přirozenou konvekcí přilehlého vzduchu. Z těchto předpokladů pak vycházely hodnoty tepelného odporu na přestupu tepla na obou stranách měřené konstrukce.

Výsledky

Porovnání výpočtů s reálným modelem konstrukce pro laboratorní měření

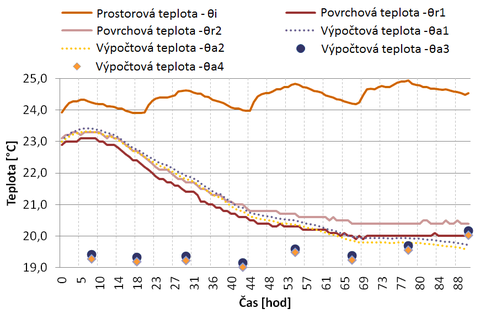
Obr. 1 – Zobrazení sledovaných teplot na „teplém“ povrchu konstrukce

Na obr. 1 je možné pozorovat reálně naměřená data na modelu (křivka značená plnou čarou), výsledky výpočtů z nestacionárního modelování povrchových teplot v programu ANSYS Workbench 12.1 [4] (křivka značená tečkovanou čárou) a výsledky výpočtu stacionárního modelování značeného jednotlivými body.

Z porovnání naměřených a simulovaných hodnot je možné vysledovat, jak je nutné k výpočtovému modelu přistupovat. Je zřejmé, že stacionární výpočet je s reálným měřením možné porovnávat až po dokončení akumulace tepla konstrukcí. K tomu v našem případě dochází po cca 4 až 5 dnech. V případě nestacionárního výpočtu je křivka z modelování velmi podobná hodnotám naměřeným a v případě delšího časového úseku by došlo k přiblížení křivek na rozdíl několika desetin °C, což je dáno ve větší míře přesností měřicího vybavení.

Vysvětlivky ke křivkám uvedeným v grafu na obr. 1

Prostorová teplota – θi

– teplota vzduchu na „teplé“ straně modelu při prováděném měření

Povrchová teplota – θr2

– reálná změřená povrchová teplota na horní straně balkónové desky

Povrchová teplota – θr3

– reálná změřená povrchová teplota na dolní straně balkónové desky

Výpočtová teplota – θa1

– simulace povrchové teploty na horní straně balkónové desky v programu ANSYS

Výpočtová teplota – θa2

– simulace povrchové teploty na dolní straně balkónové desky v programu ANSYS

Výpočtová teplota – θa3

– ustálená teplota na horní straně balkónové desky v konkrétním čase v programu ANSYS

Výpočtová teplota – θa4

– ustálená teplota na dolní straně balkónové desky v konkrétním čase v programu ANSYS

Celkově se simulace prováděné programem ANSYS ukázaly jako velmi přesné řešení porovnatelné s hodnotami naměřenými na reálném modelu. Pokud bychom byli schopni zaznamenávat velké množství dat ovlivňujících povrchové teploty na měřené konstrukcí, bylo by sladění výpočtového a reálného modelu velmi přesné.

Nejvýraznější nepřesností se v současnosti jeví nesnadné určení tepelných odporů při přestupu tepla, které mají na hodnotu povrchové teploty velmi velký vliv [5]. Z tohoto důvodu je nutné používat takové vybavení a především zařízení, které dokáže simulovat ustálené proudění po povrchu konstrukce a zabezpečit stabilní okrajové podmínky po celou dobu měření [6]. Následné vyhodnocení v příslušném programovém vybavení je sice složitější (velké množství dat, která je nutné pro jednotlivé časové úseky zadat) nicméně získané výsledky jsou výrazně přesnější [7].

Vyhodnocení reálného měření objektu na ulici Čeňka Růžičky v Brně

Obr. 2 – Termogram fasády měřeného objektu


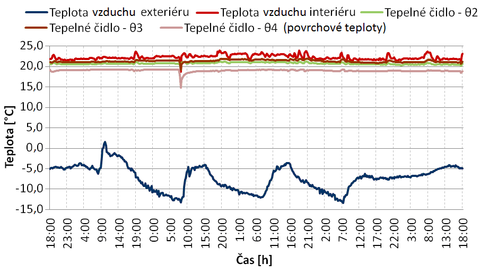
Obr. 3 – Průběh teplot (vzduchu a povrchových teplot) při měření interiérových teplot objektu Čeňka Růžičky. Tepelná čidla θ2-θ4 měřila povrchové teploty ve vybraných místech (vnitřní kout, nadpraží dveří apod.)

Ve druhém porovnání se budeme zabývat reálným měřením na reálném objektu. Pomocí termokamery (metoda infračervené termografie) jsme provedli analýzu zděného objektu na ulici Čeňka Růžičky v Brně. Na objektu bylo pozorováno větší množství tepelných mostů, především v místech arkýřů a v ploše tepelné izolace. Na obr. 2 je patrné místo napojení balkónové desky a arkýřové předsazené konstrukce. V místě styku těchto konstrukcí je pak výrazně vyšší povrchová teplota vlivem zvýšeného tepelného toku.

Při podrobném zpracování naměřených dat ze 14denního měření byl vybrán průběh teplot s nejvyšším teplotním rozdílem ΔT = 35 °C. Na grafu (obr. 3) je výběr z měření zachycujícího průběh teplot ve vybraném časovém období, kdy venkovní teplota dosahovala nejnižších hodnot. Jedná se o cca 3denní časové údobí s periodicky se opakujícími výkyvy v exteriérové teplotě.

Dále je z obr. 3 patrné kolísání vnitřních teplot v závislosti na pohybu osob a způsobu užívání místnosti. K ovlivnění vnitřní povrchové teploty dochází převážně právě provozem v interiéru. Výrazné výkyvy venkovních teplot se na průběh vnitřní povrchové teploty v podstatě neprojevují. V případě, kdy by bylo možné vnitřní provoz omezit na relativně stálé prostředí, by zcela jistě bylo možné pozorovat dopad změn venkovního klimatu. Při běžném užívání stavby je však rozhodujícím faktorem vnitřní teplota vzduchu a její výkyvy.

Výsledné měření také ukázalo, že i při návrhových podmínkách odpovídajících klimatické oblasti Brna je dobře osazený nosník zcela vyhovující a přesahuje požadovanou kritickou teplotu vnitřního povrchu o více jak 4 °C [1]. V tomto případě tomuto výsledku napomáhá i fakt, že je celý objekt z vnější strany obvodové stěny zateplen, povrchové teploty jsou pak obecně vyšší i v kritických detailech (koutech) a vlivem tepelné akumulace dochází k omezení nežádoucích teplotních výkyvů na vnitřním povrchu celé konstrukce.

Porovnání výpočtů s klimatickými daty

V posledním porovnání se budeme zabývat výsledky počítačové simulace s využitím reálně naměřených klimatických dat. Protože jsou veškeré normativní požadavky vztahovány vždy ke konkrétní hodnotě, zajímalo nás, jaké jsou rozdíly mezi teorií (normovými hodnotami) a skutečností. Vybrali jsme proto taková klimatická data, kde se extrémní vnější teplota pohybovala kolem normových okrajových podmínek. Byla pak nasimulována situace nestacionárního teplotního děje, dle těchto klimatických dat, a tyto hodnoty byly porovnány s výsledkem z modelování stacionárního teplotního pole.

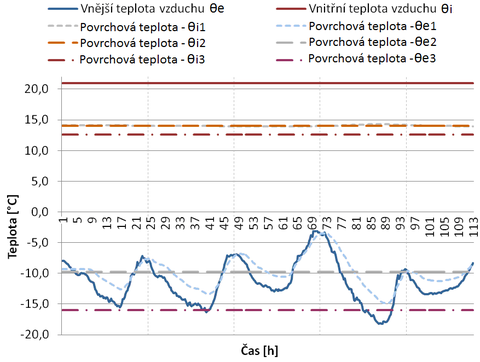
Obr. 4 – Zobrazení sledovaných teplot nestacionárního modelu na „teplém“ a „chladném“ povrchu konstrukce


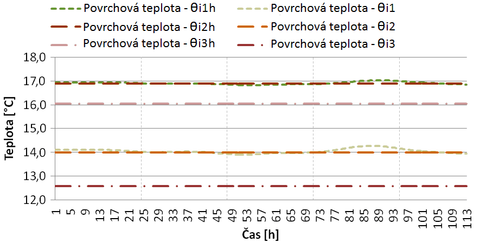
Obr. 5 – Zobrazení sledovaných teplot z nestacionárního modelu na „teplém“ povrchu konstrukce

Na obrázku obr. 4 jsou zobrazeny vybrané hodnoty pro teplou a chladnou stranu modelované konstrukce. Jednotlivé křivky simulují ustálené nebo neustálené vedení tepla (popis viz legenda). Abychom mohli sledovat, jaký vliv má rozdílný přístup na povrchové teploty, především na interiérové tj. teplé straně, musíme se podívat na následující podrobnější graf na obr. 5.

Z tohoto grafu jasně vyplývají následující zjištění. Pokud na základě naměřených venkovních hodnot použijeme hranici extrému jako podklad pro nastavení okrajové podmínky na ochlazované straně, v našem případě −18,0 °C (čerchovaná čára s jednou tečkou), dostaneme teploty neodpovídající předpokladu. Pokud z venkovních hodnot stanovíme průměrnou hodnotu (čárkovaná čára delší) okrajové exteriérové podmínky, jsou výsledky v podstatě srovnatelné s výsledky získanými z přesného nestacionárního modelování (čárkovaná čára kratší). Tato průměrná teplota je ale o celých 6,5 °C nižší než nejnižší naměřená teplota v daném období. Výsledky získané na základě výpočtu průměrné teploty dokonce ukazují o něco málo méně příznivé hodnoty, jedná se tak o výpočet orientovaný na stranu bezpečnou (avšak v přiměřené míře).

Dalším neméně zajímavým zjištěním je výkyv, k jakému dochází při změně vnitřní povrchové teploty s ohledem na proměnnost venkovní teploty. V případě největšího venkovního rozdílu, který činí cca 16 °C, došlo k výkyvu na vnitřním povrchu o pouhých několik desetin K. Toto zjištění jednoznačně potvrzuje předchozí závěry. Ovlivnění vnitřních povrchových teplot s ohledem na venkovní podmínky je velmi zanedbatelné a dochází k němu v našem případě se značným zpožděním.

Vysvětlivky ke křivkám uvedeným v grafu na obr. 4 a 5

Vnější teplota vzduchu – θe

– teplota vzduchu na „chladné“ straně modelu z reálných klimatických dat

Vnitřní teplota vzduchu – θi

– návrhová teplota vnitřního vzduchu dle ČSN 730540-2 [1]

Povrchová teplota – θi1

– simulace vnitřní povrchové teploty na dolní straně konstrukce balkónové desky v programu ANSYS dle reálných klimatických dat

Povrchová teplota – θi1h

– simulace vnitřní povrchové teploty na horní straně konstrukce balkónové desky v programu ANSYS dle reálných klimatických dat

Povrchová teplota – θe1

– simulace vnější povrchové teploty na dolní straně konstrukce balkónové desky v programu ANSYS dle reálných klimatických dat

Povrchová teplota – θi2

– simulace vnitřní povrchové teploty na dolní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −11,4 °C

Povrchová teplota – θi2h

– simulace vnitřní povrchové teploty na horní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −11,4 °C

Povrchová teplota – θe2

– simulace vnější povrchové teploty na dolní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −11,4 °C

Povrchová teplota – θi3

– simulace vnitřní povrchové teploty na dolní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −18,0 °C

Povrchová teplota – θi3h

– simulace vnitřní povrchové teploty na horní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −18,0 °C

Povrchová teplota – θe3

– simulace vnější povrchové teploty na dolní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −18,0 °C

Diskuse

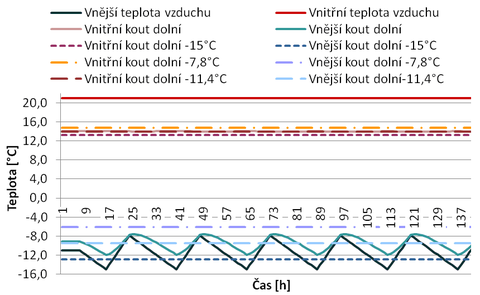
Obr. 6 – Zobrazení sledovaných teplot z nestacionárního idealizovaného modelu

Z našich výsledků se jako zajímavý jeví pohled na požadavky současných normativních předpisů. Na základě databáze venkovních teplot z Lesnické Mendlovy univerzity byl vybrán průběh teplot tak, aby co nejlépe a co nejextrémněji simuloval venkovní prostředí (obr. 6). Mezi sledovanými roky 2007 až 2011 bylo ze získaných dat možno použít pouze cca 10 dnů s teplotou pod −15 °C. Tato teplota je přitom návrhová teplota vnějšího vzduchu pro zimní období v oblasti Brna dle ČSN 730540-3:2005. Na základě provedeného porovnání je možné říci, že v našem případě vnitřní povrchová teplota stanovená na základě stacionárního stavu pro tuto okrajovou podmínku (čárkovaná čára kratší) bude srovnatelná s reálnými hodnotami povrchové teploty odpovídající návrhové hodnotě venkovního vzduchu kolem −20 °C. Nebo můžeme také říci, že v případě, kdy je návrhová teplota vnějšího vzduchu −15 °C, dosáhneme stacionárním výpočtem stejné vnitřní povrchové teploty pro okrajovou podmínku −11 °C (čárkovaná čára delší).

Je zřejmé, že normativní předpisy jsou pro masivní konstrukce orientovány významně na stranu bezpečnosti. Pokud jsme provedli zidealizování vnějších návrhových podmínek patrných z obr. 6 na stále stejně se opakující křivku vnější teploty, získali jsme hodnoty podporující naše závěry.

Vysvětlivky ke křivkám uvedeným v grafu na obr. 6

Vnější teplota vzduchu

– teplota vzduchu na „chladné“ straně modelu z idealizovaných klimatických dat

Vnitřní teplota vzduchu

– návrhová teplota vnitřního vzduchu dle ČSN 730540-2 [1]

Vnitřní kout dolní

– simulace vnitřní povrchové teploty na dolní straně konstrukce balkónové desky v programu ANSYS dle idealizovaných klimatických dat

Vnější kout dolní

– simulace vnější povrchové teploty na dolní straně konstrukce balkónové desky v programu ANSYS dle idealizovaných klimatických dat

Vnitřní kout dolní −15,0 °C

– simulace vnitřní povrchové teploty na dolní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −15,0 °C

Vnější kout dolní −15,0 °C

– simulace vnitřní povrchové teploty na horní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −15,0 °C

Vnitřní kout dolní −7,8 °C

– simulace vnitřní povrchové teploty na dolní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −7,8 °C

Vnější kout dolní −7,8 °C

– simulace vnitřní povrchové teploty na horní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −7,8 °C

Vnitřní kout dolní −11,4 °C

– simulace vnitřní povrchové teploty na dolní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −11,4 °C

Vnější kout dolní −11,4 °C

– simulace vnitřní povrchové teploty na horní straně balkónové desky v programu ANSYS pro ustálenou teplotu venkovního vzduchu −11,4 °C

Podrobnější modelování nestacionárního teplotního pole je časově náročné. Ve své podstatě sice přináší přesnější výstupy [8], ale v porovnání s přístupem prezentovaným v řadě norem zabývajících se výpočtovými postupy při ustáleném teplotním stavu se jedná o výsledky méně bezpečné. Pro praktické použití je třeba vždy uvažovat s odlišností mezi návrhem a provedením stavební konstrukce v reálných stavebních podmínkách. Proto je vhodné stavební konstrukce z hlediska teplotního faktoru vnitřního povrchu navrhovat vždy s dostatečnou rezervou.

Závěr

Na základě provedených nestacionárních simulací a měření lze konstatovat, že u masivních konstrukcí s vysokou tepelně akumulační kapacitou je průběh vnitřní povrchové teploty výrazně odlišný od situace, kdy provádíme modelování podle normativních stacionárních okrajových podmínek. V našem případě tedy konzervativní a zjednodušený přístup vycházející ze stacionárních okrajových podmínek uvedených např. v ČSN 73 0540-3:2005 je prováděn s dostatečnou rezervou, zejména v případě posuzování teplotního faktoru vnitřního povrchu. U materiálů s možností akumulace tepla při změnách skupenství bude tento rozdíl ještě výraznější.

Poděkování

Příspěvek vznikl s pomocí grantového projektu GAČR P104/12/1838 „Využití akumulace latentního tepla materiály s fázovou změnou pro snížení spotřeby primární energie v budovách“ a s finanční pomocí EU „OP Výzkum a vývoj pro inovace“, projekt reg.č. CZ.1.05/2.1.00/03.0097, v rámci činnosti regionálního Centra AdMaS „Pokročilé stavební materiály, konstrukce a technologie“.

Literatura

• [1] ČSN 73 0540-1, 2, 3, 4:2005, 2007, 2011 Tepelná ochrana budov včetně pozdějších změn a dodatků. Praha: Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, 2011. 44 p.
• [2] ŘEHÁNEK, J. Tepelná akumulace budov. Vydalo Informační centrum České komory autorizovaných inženýrů a techniků činných ve výstavby. Praha, 2002. 280 s.
• [3] ZHANG, Yinping; ZHOU, Guobing; LIN, Kunping; ZHANG, Qunli; DI, Hongfa. Application of latent heat thermal energy stoarge in buildings: State-of-the-art and outlook. Building and Environment, June 2007, vol. 42, no. 6, pp. 2197–2209. ISSN 0360-1323.
• [4] ANSYS Workbench 2.0 Framework, Version 12.1.0. © 2009 SAS IP, Inc.
• [5] ŘEHÁNEK, J. Přestup tepla na vnitřních a na vnějších površích stavebních konstrukcí. Výzkumný ústav pozemních staveb, vedoucí pracoviště vědeckotechnického rozvoje s meziodvětvovou působností. Praha, 1981. 45 s.
• [6] ČSN EN ISO 8990:1998 (73 0557) Tepelná izolace – Stanovení vlastností prostupu tapla v ustáleném stavu – Kalibrovaná a chráněná teplá skříň. Praha: Vydavatelství Český normalizační institut. 1998. 24 p.
• [7] BAGOŇA, M.; LOPUŠNIAK, M.; VERTAĽ, M. Posúdenie vybraných stavebných konštrukcií v stacionárnych aj nestacionárnych teplotných okrajových podmienkach. 121–122. Zborník prednášok z 16. medzinárodnej konferencie Tepelná ochrana budov 2011 – Aktuálne tepelnotechnické požiadavky a trendy, Thermal protection of buildings 2011. Vydání první 2011. BB Print, s.r.o. ISBN 978-80-970595-4-5.
• [8] MARTIN, K.; ERKOREKA, A.; FLORES, I.; ODRIOZOLA, M.; SALA, J. M. Problems in the calculation of thermal bridges in dynamic conditions. Energy and Buildings 43 (2011) 529–535. ISSN: 0378-7788.