Stanovení nosné a dělicí funkce lehkých skeletů dřevostaveb za požáru
Chování dřeva za požáru je velmi dobře předvídatelný jev. Pomocí zjednodušených výpočetním metod lze stanovit nosnou a dělicí funkci konstrukcí. U tyčových nosných prvků se jedná o parametr R (únosnost a stabilita), u plošných – svislých nebo vodorovných konstrukcí jde o mezní kritéria R, E, I (nosnost, celistvost, izolace). V mnoha případech je velmi obtížné a dle Eurokódu 5 (1–2) téměř nemožné stanovit čas počátku zuhelnatění dřevěného prvku pod protipožární ochranou a čas porušení protipožární ochrany.
1 Úvod
Kromě stanovení nosné funkce (parametr R), lze podle Eurokódu 5 (část 1–2) u stěn a stropů stanovit i jejich dělicí funkci (parametr R a I). Pomocí Eurokódu 5 (1–2) je možné tyto výpočty provádět zjednodušeně. K dispozici je celá řada výpočetních programů založených na metodě konečných prvků a pomocí nich lze stanovit hloubku zuhelnatění, rozvoj a rozdělení teploty uvnitř konstrukčních prvků (model tepelné odezvy) a vyšetřit konstrukční chování konstrukce nebo její libovolné části (model konstrukční odezvy).
Při posuzování dřevěných konstrukcí vystavených účinkům požáru je třeba vzít v úvahu to, že rychlost zuhelnatění je v případě chráněného prvku rozdílná, než v případě nechráněného. Pokud protipožární ochranné obložení odpadne, například následkem ztráty přilnavosti nebo selháním uchycení, rychlost zuhelnatění chráněného prvku bude vyšší než rychlost zuhelnatění nechráněného prvku. Pokud protipožární ochranné obložení zůstává přichycené k dřevěnému prvku, rychlost zuhelnatění bude ovlivněna izolačním účinkem protipožárního ochranného obložení.
2 Stanovení nosné funkce lehkých skeletů za požáru
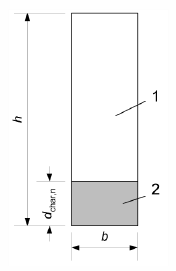
Obrázek 1 Nominální zbytkový průřez prvku dřevěného rámu chráněného izolací v dutině (ČSN EN 1995-1-2)
Legenda
- Nominální zbytkový průřez
- Nominální vrstva zuhelnatění
Pro stanovení nosné funkce stropních nosníků a sloupků stěn v sestavách, jejichž dutiny jsou zcela vyplněny izolací, slouží Příloha C (ČSN EN 1995-1-2). Podle obr. 1 se má určit nominální zbytkový průřez, kde nominální hloubka zuhelnatění je dána vztahem:
kde
- dchar, n
- – nominální návrhová hloubka zuhelnatění, která zahrnuje účinek zaoblení rohů;
- βn
- – nominální návrhová rychlost zuhelnatění, jejíž rozsah zahrnuje účinek zaoblení rohů;
- t
- – doba vystavení účinkům požáru.
A nominální rychlost zuhelnatění je určena podle následujících vztahů:
nebo
| b [mm] | ks |
|---|---|
| 38 | 1,4 |
| 45 | 1,3 |
| 60 | 1,1 |
kde
- βn
- – nominální návrhová rychlost zuhelnatění;
- ks
- – součinitel průřezu (viz tabulka 1);
- k2
- – součinitel izolace;
- k3
- – součinitel dodatečné ochrany;
- kn
- – součinitel převádějící nepravidelný zbytkový průřez na nominální obdélníkový průřez (= 1,5);
- tch
- – čas počátku zuhelnatění prvku dřevěného rámu;
- tf
- – čas porušení obvodového pláště.
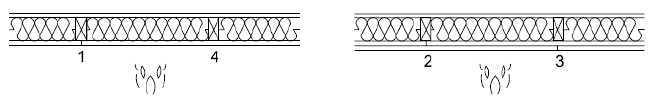
Obrázek 2 Uspořádání spojů v sádrokartonových deskách s jednou a dvěma vrstvami (ČSN EN 1995-1-2)
Součinitel izolace se pro obvodové pláště ze sádrokartonové desky typu F nebo kombinace typu F a typu A s typem F jako vnější vrstvou se může určit takto:
- v místech, kde je obvodový plášť beze spoje (obr. 2 – 4) nebo pro uspořádání podle obr. 2 – 2:
- pro uspořádání spoje dle obr. 2 – 1 a 3:
kde
- hp
- – celková tloušťka všech vrstev desky [mm]
Součinitel dodatečné ochrany se, za předpokladu, že izolace dutiny je provedena z rohoží z minerálních vláken a zůstane v poloze po poškození obložení, vypočítat takto:
kde
- tf
- – čas porušení obložení [min]
V případech, kdy je provedena izolace dutiny ze skelného vlákna, se má předpokládat, že porušení prvku nastane v čase tf.
Příloha D, ČSN EN 1995–1–2 popisuje zuhelnatění prvků v sestavách stěn a stropů s prázdnými dutinami.
3 Analýza dělicí funkce stěnových a stropních sestav dle ČSN EN 1995-1-2
Pro analýzu dělicí funkce stěnových a stropních sestav slouží příloha E. Předpokládá se, že požadavky na celistvost (E) jsou splněny, pokud jsou splněny požadavky na izolaci (I) a desky zůstávají připojeny k dřevěnému rámu na straně nevystavené požáru.
Pro dělicí prvky se má ověřit, že čas potřebný pro dosažení vzrůstů teploty na straně nevystavené požáru tinst je menší nebo roven požadované době požární odolnosti pro dělicí funkci sestavy treq.
Kritérium izolace I je splněno, pokud průměrný vzestup teplot na celém požáru nevystaveném povrchu je omezen na 140 K a maximální vzestup teploty v kterémkoliv bodě povrchu nebude větší než 180 K.
Hodnota tinst se má vypočítat jako součet příspěvků jednotlivých vrstev použitých v konstrukci:
kde
- tinst,0,i
- – základní izolační hodnota vrstvy i [min]
- kpos
- – součinitel polohy;
- kj
- – součinitel spoje.
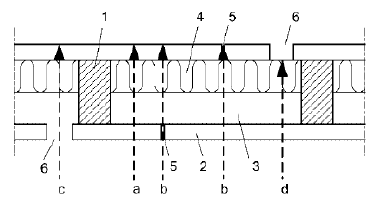
- Prvek dřevěného rámu
- Deska
- Prázdná dutina
- Izolace dutiny
- Spoj desky nekrytý latí, sloupkem nebo stropnicí
- Poloha instalací
a-d Dráha sdílení tepla
Spoj nemá vliv na dělicí užitné vlastnosti, jestliže je kryt latí nebo konstrukčním prvkem, které zabraňují přístupu horkých plynů do konstrukce. Možné způsoby drah sdílení tepla je patrný z obr. 3.
4 Zpřesněné výpočetní metody
Zpřesněné výpočetní metody mohou být použity pro:
- stanovení hloubky zuhelnatění;
- rozvoj a rozdělení teploty uvnitř konstrukčních prvků (model tepelné odezvy);
- vyšetřování konstrukčního chování konstrukce nebo její libovolné části (model konstrukční odezvy).
Přestup tepla konstrukcí se počítá pomocí tepelně závislých koeficientů podle ČSN EN 1991-1-2. Tepelná zatížení jsou dána čistým tepelným tokem h‧net [W/m2] dopadajícím na povrch prvku. Na plochách, které jsou vystaveny účinku požáru, se má tento čistý tepelný tok stanovit se zahrnutím přenosu tepla prouděním a sáláním takto:
kde
- h‧net,c
- – složka čistého konvekčního tepelného toku daná vztahem (4.2)
- h‧net,r
- – složka čistého sálavého tepelného toku daná vztahem (4.3)
kde
- αc = 25
- – součinitel přestupu tepla prouděním, na odvrácené straně dělicího prvku αc = 4 [W/m2K];
- Θg
- – teplota plynů v blízkosti prvku vystaveného účinkům požáru [°C];
- Θm
- – povrchová teplota prvku [°C].
kde
- φ = 1,0
- – polohový faktor;
- εm = 0,8
- – povrchová emisivita prvku;
- εf = 1,0
- – emisivita požáru;
- σ = 5,67‧10−8
- – Stephan-Boltzmannova konstanta [W/m2K4];
- Θr
- – účinná teplota sálání prostředí požáru [°C];
- Θm
- – povrchová teplota prvku [°C].
4.1 Nestacionární vedení tepla
Výpočet teplotních polí vychází z Fourierovy parciální diferenciální rovnice nestacionárního vedení tepla, kterou lze vyjádřit diferenčním tvarem:
a) Pro vedení tepla v jednom směru:
b) Pro vedení tepla ve dvou směrech:
kde
- ΔT
- – přírůstek teploty [°C];
- Δt
- – přírůstek času [s];
- Δx
- – tloušťka vrstvy ve směru osy x [m];
- Δy
- – tloušťka vrstvy ve směru osy y [m];
- a
- – součinitel teplotní vodivosti [m2.s−1].
Součinitel teplotní vodivosti a lze vyjádřit vztahem:
kde
- λ
- – součinitel tepelné vodivosti [W.m−1K−1];
- c
- – měrné teplo [J.kg−1.K−1];
- ρ
- – objemová hmotnost [kg.m−3].
Podmínky správnosti početního řešení je znalost přestupu tepla a tepelně technických parametrů materiálů izolujících a vyplňujících dřevěný rám. Tyto parametry jsou s teplotou proměnné, proto je potřeba znát jejich hodnoty v závislosti na teplotě (Karpaš, 1984).
5 Závěr
Chování dřeva za požáru je velmi dobře předvídatelný jev. Pomocí zjednodušených výpočetním metod lze stanovit nosnou a dělicí funkci konstrukcí. U tyčových nosných prvků se jedná o parametr R (únosnost a stabilita), u plošných – svislých nebo vodorovných konstrukcí jde o mezní kritéria R, E, I (nosnost, celistvost, izolace). V mnoha případech je velmi obtížné a dle Eurokódu 5 (1–2) téměř nemožné stanovit čas počátku zuhelnatění dřevěného prvku pod protipožární ochranou a čas porušení protipožární ochrany. V této oblasti jsou stále určité nedostatky a je nezbytné provádět požární zkoušky, aby se zvýšila míra poznání a bylo možné dále rozvíjet a zpřesňovat výpočetní metody.
Poděkování
Tento příspěvek byl zpracován za podpory projektu SGS ČVUT, SGS11/108/OHK1/2T/11 „Požární odolnost vícepodlažních budov na bázi dřeva“.
Odkazy
- [1] ČSN EN 1991-1-2 Zatížení konstrukcí, část 1–2: Zatížení konstrukcí vystavených účinkům požáru. ČNI Praha, 2006
- [2] ČSN EN 1995-1-2 Eurokód 5: Navrhování dřevěných konstrukcí – Část 1–2: Obecná pravidla – Navrhování konstrukcí na účinky požáru. ČSNI, Praha 2006
- [3] Karpaš, J. Směrnice pro výpočet požární odolnosti ocelových konstrukcí, Výzkumný ústav pozemních staveb, Praha, 1984
The fire behavior of wood is very predictable phenomenon. Using the simplified computational methods it can be determined the bearing and separating function of structures. The bar-shaped load-bearing elements is a parameter R (resistance and stability) for PCB - vertical and horizontal structures for the threshold criteria R, E, I, (capacity, integrity, insulation). In many cases it is very difficult and according to Eurocode 5 (1-2) almost impossible to determine the start time charring timber under fire protection and fire protection violation time.