Problémy při stanovení prostupu tepla zeminou
Součinitel prostupu tepla konstrukcemi přilehlými k zemině počítaný přibližnými metodami podle ČSN EN ISO 13370 je odlišně definovaný proti definicím v dalších normách, např. v ČSN EN ISO 6946, přitom s ohledem na stavební praxi nejsou přibližné výpočty uvedené v ČSN EN ISO 13370 příliš výstižné.
Úvod
Výpočty přenosu tepla zeminou podle ČSN EN ISO 13370 [1] a ČSN EN ISO 10211 [2] jsou výjimečné. Vybočují nejen specifickým předmětem zájmu, ale i zcela odlišnou filosofií výpočtového stanovení fyzikálních veličin. Po bližším ohledání je zřejmé, že je to bohužel v rozporu s platnými definicemi i v rozporu s reálnými fyzikálními ději. Pokusíme se přiblížit důvody pro toto tvrzení.
Součinitel prostupu tepla U konstrukcí přilehlých k zemině
Součinitel prostupu tepla U je obecně v terminologii [3] definován jako ustálený tepelný tok jednotkou plochy konstrukce pro jednotkový teplotní spád přilehlých prostředí, tedy v případě zeminy s teplotou ϴg:
V ČSN EN ISO 13370 [1] je však veličina užívající shodnou značku U a shodně nazývaná „součinitel prostupu tepla“ definovaná odlišně – jako ustálený tepelný tok jednotkou plochy konstrukce pro základní teplotní spád (tj. teplotní rozdíl mezi vnitřním prostředím ϴi a venkovním prostředím ϴe), který se ale u konstrukcí přilehlých k zemině liší od skutečného teplotního spádu přilehlých prostředí. Označíme-li si pro rozlišení tento součinitel prostupu tepla podle normy [1] U13370, pak platí:
Lze předpokládat, že tento nesystémový přístup byl zvolen účelově v představě určitého zjednodušení (a vypuštění nejisté okrajové podmínky – teploty v zemině) při výpočtech měrných toků tepla zeminou. V konečném důsledku je však tento přístup spíše zdrojem komplikací a zmatků.
První komplikací je skutečná velikost nově definovaného součinitele prostupu tepla U13370, kterou lze vyjádřit vztahem:
Teplotní redukční činitel bg pro prostup tepla zeminou (takto je definovaný v ČSN 73 0540-4 [6], příl. H. 2) plně odpovídá definici této veličiny pro jiné případy prostupu tepla do jiného prostředí než je venkovní vzduch podle tepelně technické ČSN EN ISO 13789 [4], nebo podle topenářské ČSN EN 12831 [5]. Z toho je zřejmé, že požadavek pro hodnoty U13370 stanovené podle [1] musí být nutně redukován teplotním redukčním činitelem bg pro prostup tepla zeminou a bude tedy zdánlivě přísnější, než požadavek na součinitel prostupu tepla podle korektní definice v ČSN EN ISO 6946 [7] a v [3]. Pokud se používají obě veličiny (a neexistuje racionální důvod pro vyloučení tradičního hodnocení s fyzikálně správnou definicí součinitele prostupu tepla), pak se nutně musí rozlišit i dva různé požadavky.
Druhou komplikací jsou obtíže při vzájemném porovnávání výsledků hodnocení lineárních tepelných vazeb detailů stěn a podlah přilehlých k zemině získaných řešením teplotních polí. Srovnání výsledků různých hodnotitelů zkreslují přípustné odlišnosti v zadávaném geometrickém modelu s extrémními rozměry, které jsou zřejmě volené pro potlačení vlivu nevhodné adiabatické podmínky na jeho spodní hranici.
Adiabatická podmínka na spodní hranici výpočtového modelu
Adiabatickou podmínku (hranici) si můžeme představit jako hranici, přes kterou nedochází k výměně tepla – tepelný tok přes tuto hranici je nulový. Ve výpočtu tepelných toků v zemině podle [2], je adiabatická podmínka daná spodní hranicí výpočtového modelu. To znamená, že v tomto modelu veškerý tepelný tok přes konstrukce v kontaktu se zeminou, prochází zeminou do venkovního prostředí. Ve skutečnosti ale část tepla zůstává v zemině a pouze část tepelného toku přes suterénní stěny, v oblasti základů nebo přes okraje základové desky, se dostává do venkovního prostředí.
Pokud tedy [1] a [2] vyžadují uplatnění této adiabatické podmínky v různých, často nesmyslně velkých hloubkách pod budovou, pak záměrně (či z neznalosti) deformují fyzikální děj a vnáší do výsledku hodnocení zbytečnou systémovou chybu, která nutně zkresluje naši představu o tepelně-energetickém chování budovy. V grafickém znázornění se tato chyba projevuje izotermami kolmými na spodní hranici a zápornými teplotami i ve velkých hloubkách pod povrchem. Izotermy by ale měly být převážně rovnoběžné s touto hranicí, stejně jako u modelu pro výpočet povrchových teplot podle [2], kdy se zadává okrajová podmínka s průměrnou roční venkovní teplotou 3 m pod úrovní terénu.
Je pochopitelné, že volba velkých vzdáleností u modelu pro výpočet tepelného toku je vedena snahou o potlačení této chyby. To však má za následek další rozpor se skutečností – nereálné uvažování vlastností zeminy ve větších hloubkách. Je to dáno tím, že výškový profil skladby hornin je výrazně proměnlivý, stejně tak jako jejich zvodnění. Tepelné chování zeminy ve větších hloubkách je velkou neznámou a obvykle je uvažováno zcela nereálně.
Víme přitom, že v určité nepříliš proměnné hloubce zeminy lze předpokládat teplotu ve výši průměrné roční venkovní teploty. Určitě by proto bylo správnější uvažovat spodní hranici modelu v této hloubce a to zadáním průměrné roční venkovní teploty na této hranici (podle [2] pro výpočet povrchových teplot je tato hranice v hloubce nejméně 3 m pod povrchem).
Vzdálenost hranic výpočtového modelu
Vzdálenost vnější boční hranice modelu pro výpočet tepelného toku podle [2] je vázána na šířku podlahy (2,5 × šířka podlahy). Vezmeme-li průměrný RD s šířkou podlahy 10 m, vychází vzdálenost vnější boční hranice (roviny řezu) 12,5 m, což může být méně, než vzdálenost k sousednímu domu, který také ovlivňuje teplotní pole v zemině. U řadových domů je to extrémně špatně. V těchto případech by hranice měla být v pomyslné ose symetrie mezi sousedními domy.
Stejně tak je problémem velká vzdálenost hranic (bočních, ale i hranice spodní) v případě hodnocení tepelných toků u výrobních hal, kdy se šířka haly pohybuje řádově v desítkách, někdy i stovkách metrů. Vzdálenost hranic výpočtového modelu pak vychází taková, že ji není možné vůbec zadat do výpočetního programu.
Lineární činitele prostupu tepla
Princip výpočtu lineárního činitele prostupu tepla Ψ spočívá v porovnání tepelné propustnosti ideálních výseků příslušných částí konstrukcí s propustností celého detailu (tedy vč. tepelné vazby), stanovené podrobným výpočtem 2D nebo 3D teplotního pole. Postup je definovaný v [2], která se ale u konstrukcí přilehlých k zemině odkazuje na [1].
Prvním problémem v tomto případě je použití součinitele prostupu tepla konstrukce Ug, který se stanovuje podle [1] vč. vlivu přilehlé zeminy. Díky tomu se nehodnotí vliv materiálové či tvarové nedokonalosti řešení tepelné vazby (charakterizované Ψ), ale spíš odchylka přibližných vzorců od podrobnějšího řešení teplotního pole. Lineární vazba podle [2] je tak charakterizována vč. určitého (neznámého) podílu vlivu zeminy a nevyjadřuje již (anebo velmi vzdáleně) konstrukční kvalitu či nekvalitu, dokonalost či nedokonalost samotného řešení konstrukčního detailu. Tím také nemůže být vodítkem pro vhodné konstrukční úpravy.
Dalším problémem je aplikovatelnost výpočtové metody podle [2] pouze na jednoduché příklady podlah na zemině. U složitějších detailů (viz obrázek) je nutno zavádět do výpočtu různé další předpoklady a zjednodušení, které si navíc musí řešitel (projektant) často sám vymýšlet a vnitřně obhájit. Tím jsou ale zase vnášeny do výpočtu další a další chyby, které konečný výsledek ještě více znevěrohodňují.
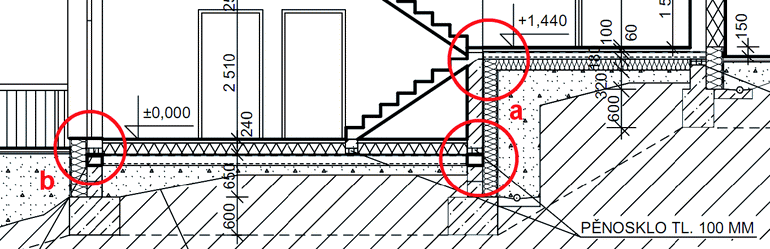
Příklady složitějších detailů pro hodnocení tepelných vazeb: a) částečné podsklepení, b) francouzské okno na základové desce
Tepelná ztráta konstrukcí přilehlou k zemině
Tepelná ztráta (tepelný tok) přes konstrukci se obecně stanoví podle vztahu:
Pokud se uvažuje jednotkový teplotní spád přilehlých prostředí, označuje se tato tepelná ztráta jako „měrná“ – HT (pokud na konstrukci působí jiný teplotní spád než základní, zohlední se v HT tzv. teplotním redukčním činitelem b).
Pro výpočet tepelné ztráty konstrukcí přilehlou k zemině lze použít některý ze tří postupů, uvedených v platných technických normách:
Podle ČSN 73 0540-4 [6], příl. H 2
Problémem tohoto postupu je nejistá teplota v zemině ϴg, která se zadává do výpočtu teplotního redukčního činitele b.
Podle ČSN EN 12831 [5]
Problémem tohoto postupu je ekvivalentní součinitel prostupu tepla s vlivem zeminy Uequiv, stanovený pro různé typologie podlah – tento je uveden pouze pro určité hodnoty samotného součinitele prostupu tepla U konstrukce (podlahy nebo stěny) přilehlé k zemině a pouze pro její určité hloubky pod povrchem terénu. Pro ostatní hodnoty U a jiné hloubky pod povrchem, se dá získat Uequiv jedině interpolací nebo pomocí některého výpočetního programu.
Další otázkou zůstává stanovení Uequiv pro stěny a podlahy při různých hloubkách pod úrovní terénu – např. při částečném podsklepení. Tepelné toky přes suterénní stěnu a výše položenou podlahu se vzájemně ovlivňují – ve výpočtu Uequiv obou konstrukcí se však s tímto vzájemným ovlivňováním neuvažuje.
Podle ČSN EN ISO 13370 [1]
se všemi problémy uvedenými v předchozích kapitolách.
V následující tabulce jsou uvedeny tepelné ztráty stanovené výše uvedenými postupy (vč. modelování 2D teplotního pole) přes podlahovou základovou desku pasivního domu. Součinitel prostupu tepla samotné podlahy (bez vlivu zeminy): U = 0,12 W/(m2·K).
| Metodika | Tepelná ztráta Q [W] | Měrná tepelná ztráta HT [W/K] |
| model 2D teplotního pole podle ČSN EN ISO 10211 | tepelná propustnost L2D: 0,457 W/(m·K) | 5,20 |
| ČSN 73 0540-4 | --- | 4,38 |
| ČSN EN 12831 | 150 | 4,27 |
| ČSN EN ISO 13370 | --- | 9,07 |
| ČSN 06 0210 | 153 * | --- |
* v tomto případě se neuvažoval „zabudovaný“ součinitel prostupu tepla s vlivem zeminy podle ČSN 73 0540-4/1994
Pokud vezmeme za základ hodnotu HT, stanovenou relativně nejpřesnějším postupem (na základě 2D modelu teplotního pole v zemině pod podlahou podle [2]), lze konstatovat, že tepelné ztráty stanovené zjednodušenými postupy se příliš neliší (a to ani v případě už tolikrát odepsané [8]). Zajímavá je poměrně vysoká hodnota HT, stanovená dle [1] – v tomto konkrétním případě se zřejmě negativně projevuje „překombinovaný“ zjednodušený výpočet.
Je však nutno zdůraznit, že tyto výsledky platí jen a pouze pro tuto danou konkrétní podlahu – pro jiné typy podlah (s jiným tepelným odporem nebo jinak umístěnou) mohou být výsledky a jejich interpretace odlišné.
Závěr
Příspěvek poukazuje na úskalí při výpočtu prostupu tepla konstrukcemi přilehlými k zemině podle evropské normy [1], citované také v [2]. Tyto výpočtové metody nezahrnují některé (složitější) praktické případy, a přestože jsou v [1] označeny jako „zjednodušené“, běžný uživatel (projektant) bez patřičného programového vybavení a zaškolení si s nimi neporadí. Navíc tyto převzaté metody pracují s „nestandardními“ fyzikálními předpoklady a postupy, což může vést k nesprávným výsledkům, se všemi z toho vyplývajícími možnými důsledky. Cílem příspěvku je vyvolat diskuzi o nutnosti úprav či oprav uvedených normových metod a vhodnosti znovuzavedení alternativní metody výpočtu v ČSN 73 0540-4.
Literatura
- [1] ČSN EN ISO 13370 (73 0559) Tepelné chování budov – Přenos tepla zeminou – Výpočtové metody
- [2] ČSN EN ISO 10211 (73 0551) Tepelné mosty ve stavebních konstrukcích – Přenos tepla zeminou – Výpočtové metody
- [3] ČSN 73 0540-1 Tepelná ochrana budov – Část 1: Terminologie
- [4] ČSN EN ISO 13789 (73 0565) Tepelné chování budov – Měrná ztráta prostupem tepla – Výpočtová metoda
- [5] ČSN EN 12831 (06 0206) Tepelné soustavy v budovách – Výpočet tepelného výkonu
- [6] ČSN 73 0540-4 Tepelná ochrana budov – Část 4: Výpočtové metody
- [7] ČSN EN ISO 6946 Stavební prvky a stavební konstrukce – Tepelný odpor a součinitel prostupu tepla – Výpočtová metoda
- [8] ČSN 06 0210 Výpočet tepelných ztrát budov při ústředním vytápění
1 Ing. Vladan Panovec, VŠB-TU Ostrava, FAST, Ludvíka Podéště 1875/17, 708 33 Ostrava, vladan.panovec@vsb.cz
2 Ing. Jiří Šála, CSc. – MODI, Nitranská 19, 130 00 Praha 3-Vinohrady, salamodi@volny.cz
Calculations of heat transfer through soil according to ISO 13370 [1] and EN ISO 10211 [2] are rare. They stands out not only for the specific subject of interest, but also for a completely different philosophy of the calculation for determining the physical quantities. It is clear that this is unfortunately in conflict with the definitions and in conflict with real physical phenomenons. We try to approach the reasons for this assertion.