Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Roh zasklívací jednotky – metodika pro odhad `f`_Rsi v rohu zasklení

1.6.2015

Ing. Roman Jirák, Ph.D., Decoen v.o.s.

Recenzovaný

Povrchová teplota jako jeden z nejsledovanějších parametrů otvorových výplní a lehkých obvodových plášťů nejen v České republice posuzuje konstrukce z pohledu rizika kondenzace vodních par, resp. z pohledu jejich zdravotní a hygienické závadnosti či nezávadnosti vzhledem k prostředí, do kterých jsou zabudovávány. Jejím smyslem je určení, zdali daná konstrukce je vhodná pro konkrétní okrajové podmínky nebo je nutné zvolit konstrukci odlišnou.

Předkládaný článek si klade za cíl vyvinout jednoduchou použitelnou metodiku pro stanovení resp. odhad teplotního faktoru v nejkritičtějším místě okenních konstrukcí, kterou je zasklívací spára. Minulý článek ukázal zjednodušenou metodiku pro stanovení f_Rsi na charakteristickém průřezu rámu. Protože však nejkritičtější místo se vyskytuje v rohu zasklívací jednotky, bylo nutné vyvinout metodiku pro odhad teplotního faktoru v tomto místě.

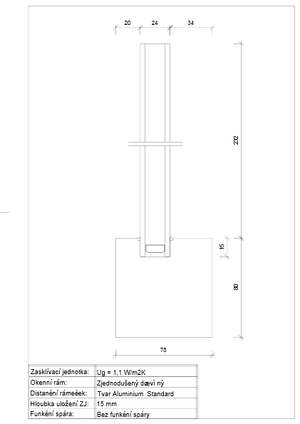
Obrázek č. 1 Zjednodušená konstrukce použitá pro výpočty

Nejvhodnější způsob, jak určit teplotní faktor i v nejkritičtější oblasti, je odvození závislosti mezi teplotními faktory v zasklívací spáře uprostřed vlysu (charakteristický průřez) a v rohu zasklení. Jsou známé tři majoritní faktory ovlivňující povrchovou teplotu v oblasti zasklívací spáry na charakteristickém průřezu rámu. Lze bez pochyby předpokládat, že i tyto faktory budou majoritně ovlivňovat vztah mezi analyzovanými povrchovými teplotami. Jejich kombinace by však znamenala skupinu téměř tří stovek výpočtů, které nejen díky časové náročnosti třírozměrných simulací nelze provést. Je tedy nutné nalézt proměnnou, která by s určitou přesností tyto faktory nahrazovala. Jestliže druhem distančního rámečku, hloubkou uložení zasklívací jednotky a změnou druhu materiálu okenního rámu je ovlivňována povrchová teplota, musí jimi být ovlivňována i míra přídavného tepelného toku způsobená napojením zasklívací jednotky a okenního rámu. Pro charakteristiku tohoto přídavného tepelného toku je již dávno známá veličina, a tou je lineární součinitel prostupu tepla zasklívací spáry ψ [W/mK]. V nadcházejících třírozměrných výpočtech místo kombinace předešlých tří faktorů byly použity různé hodnoty lineárního součinitele prostupu tepla. Díky již zmíněné složitosti třírozměrných výpočtů byl použit zjednodušený model zobrazený na obrázku č. 1.

Byl vymodelován zjednodušený dřevěný okenní rám (měkké dřevo – λ = 0,13 W/mK) o tloušťce 78 mm s užitím anizotropických vlastností dřeva se zasklívací jednotkou o součiniteli prostupu tepla U_g = 1,1 W/m²K a hloubkou uložení 15 mm. Byl namodelován tvar distančního rámečku Aluminium Space Bar Bentable kvůli svým relativně velkým rozměrům a možnosti přesného síťování. Pro jednotlivé výpočty byla měněna tepelná vodivost distančních rámečků tak, aby reprezentovala určitou hodnotu lineárního součinitele prostupu tepla zasklívací spáry.

Zjednodušení modelu vycházela především ze dvou hlavních příčin. Pro zjištění závislosti bylo nutné provést několik výpočtů, a to pro složitý model, jaký okenní konstrukce bezpochyby představuje, není možné především díky časové a hardwarové náročnosti výpočtů. Dále pak není známá ekvivalentní tepelná vodivost vzduchových dutin ve třetím směru a jejich nesprávné zadání by mohlo výrazně zkreslovat výsledky.

Prvním krokem zkoumání závislosti povrchových teplot bylo vypočtení tepelné vodivosti těla distančního rámečku pro zvolené hodnoty lineárních součinitelů prostupu tepla. Výpočty lineárních součinitelů prostupu tepla byly provedeny v programu Flixo dle platných ČSN EN ISO 10077-2. Hodnoty těchto přídavných tepelných toků byly zvoleny v rozmezí 0,03–0,08 W/mK. Tabulka č. 1 uvádí tepelné vodivosti těla distančního rámečku a pro ně vypočtené hodnoty lineárního součinitele prostupu tepla zasklívací spáry.

Tabulka č. 1 Tepelná vodivost těla distančního rámečku a lineární součinitel prostupu tepla zasklívací spáry
`λ` [W/mK]	`ψ` [W/mK]
72	0,08
14	0,07
5,55	0,06
2,15	0,05
0,355	0,04
0,0012	0,03

Zavedení lineárního součinitele prostupu tepla jako hodnoty nahrazující vliv majoritních faktorů ovlivňujících povrchovou teplotu v oblasti zasklívací spáry je velmi praktické, protože pro danou kombinaci distančního rámečku a okenního rámu je tento součinitel dobře znám a každý výrobce jej uvádí. Samozřejmě jeho použití při stanovení hodnoty teplotního faktoru by bylo značně nepřesné, ale lze předpokládat, že pro stanovení vztahu mezi touto hodnotou v rohu zasklívací jednotky a na charakteristickém průřezu rámu je dostačující.

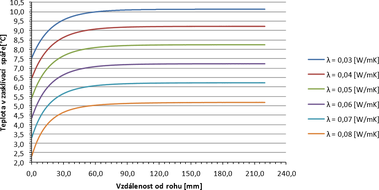
Graf č. 1 Průběh povrchových teplot v oblasti zasklívací spáry v závislosti na vzdálenosti od rohu zasklení

Bylo provedeno šest výpočtů ve třírozměrném teplotním poli pro tepelné vodivosti distančního rámečku zobrazené v předcházející tabulce č. 1. Výsledné teploty jsou zobrazeny v grafu č. 1, kde na ose x je vynesena vzdálenost od rohu zasklení a na ose y vypočtená teplota v oblasti zasklívací spáry. Je patrné, že chování povrchových teplot má shodný průběh nezávisle na lineárním součiniteli prostupu tepla zasklívací spáry. Ve směru od rohu zasklení se teplota v oblasti zasklívací spáry prudce zvyšuje a ve vyšších vzdálenostech od rohu se postupně vyrovnává. Teploty v rohu zasklené a teplota na konci křivky (na charakteristickém průřezu rámu) vykazují mezi sebou určitou závislost. Zda se tento poměr mění a jakým způsobem v závislosti na lineárním součiniteli prostupu tepla, nelze z grafu č. 1 vypozorovat.

Stejně jako v předešlých částech článku je i pro určení vztahu povrchových teplot vhodné použít vyjádření pomocí teplotního faktoru vnitřního povrchu. Jen takto je možné zajistit poměr, který bude závislý pouze na geometrii a charakteristice konstrukce (v tomto případě na lineárním součiniteli prostupu tepla), a nikoliv na okrajových podmínkách. V následující tabulce č. 2 jsou pro všechny výpočty uvedeny hodnoty povrchových teplot a k nim vypočtené teplotní faktory v rohu zasklení f_Rsi,min a na charakteristickém průřezu rámu f_Rsi,max. V posledním sloupci je v procentech vyjádřen jejich zkoumaný vzájemný vztah.

Tabulka č. 2 Procentuální závislost teplotního faktoru na charakteristickém průřezu rámu a rohu zasklení
`λ` [W/mK]	`ψ` [W/mK]	`ϑ`_si,min [°C]	`f`_Rsi,min [–]	`ϑ`_si,max [°C]	`f`_Rsi,max [–]	(`f`_Rsi,min / `f`_Rsi,max) . 100 [%]
72	0,08	2,32	0,481	5,17	0,560	85,89
14	0,07	3,33	0,509	6,23	0,590	86,35
5,55	0,06	4,37	0,538	7,24	0,618	87,07
2,15	0,05	5,42	0,567	8,24	0,645	87,89
0,355	0,04	6,50	0,597	9,21	0,673	88,78
0,0012	0,03	7,54	0,626	10,12	0,698	89,74

Je patrné, že se snižujícím se lineárním součinitelem prostupu tepla zasklívací spáry se procento pomalu zvyšuje. Jinými slovy, čím menší tepelný most distanční rámeček tvoří nebo čím více je zastíněn pomocí okenního rámu, tím více se přibližuje povrchová teplota, resp. hodnota teplotního faktoru v rohu zasklení k hodnotě na charakteristickém průřezu. Z těchto dat lze vyvinout novou rovnici, určující vztah mezi teplotním faktorem vnitřního povrchu v zasklívací spáře v rohu zasklení a na charakteristickém průřezu rámu a zároveň zavádějící nový činitel.

f_Rsi-C = γ_ψ ‧ f_Rsi

kde platí:

f_Rsi: … teplotní faktor v zasklívací spáře na charakteristickém průřezu rámu [–]
f_Rsi-C: … teplotní faktor v zasklívací spáře v rohu zasklení [–]
γ_ψ: … korekční činitel rohu zasklívací spáry [–]

Nově zavedený korekční činitel rohu zasklívací spáry γ_ψ je bezrozměrné číslo určující vztah mezi teplotními faktory v zasklívací spáře v rohu a na charakteristickém průřezu rámu pro daný lineární součinitel prostupu tepla zasklívací spáry ψ. Korekční činitel stanovuje následující rovnice, která ručuje jeho závislost na lineárním součiniteli prostupu tepla.

γ_ψ = 98,739ψ³ ‧ 10,662ψ² ‧ 0,555ψ ‧ 0,921

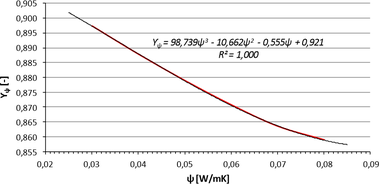
Graf č. 2 Závislost korekčního činitele rohu zasklení na lineárním součiniteli prostupu tepla zasklívací spáry

Rovnice vychází z křivky zobrazené v následujícím grafu č. 2, který byl vynesen na základě výsledků třírozměrných výpočtů. Křivkou byla proložena, pro stanovení nejpravděpodobnější závislosti, polynomická spojnice trendu třetího řádu. Pro spojnici byla dále stanovena rovnice regrese, která udává výše popsanou závislost mezi lineárním součinitelem prostupu tepla zasklívací spáry a korekčním činitelem rohu zasklení. Koeficient spolehlivosti R uvedený v grafu pod rovnicí dosahuje hodnoty 1, což reprezentuje naprostou matematickou přesnost popisu rovnice křivky.

Validace výpočtu

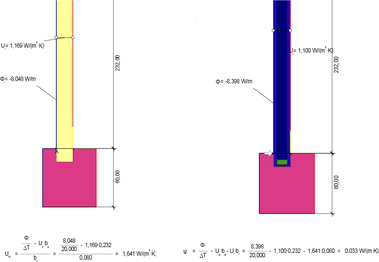
Obrázek č. 2 Výpočet lineárního součinitele prostupu tepla

Aby bylo možné stanovenou rovnici a korekční součinitel rohu rámu považovat za věrohodné, používat je pro odhady teplotních faktorů v rohu zasklívací spáry okenních konstrukcí a do určité míry jimi nahradit obtížné a složité třírozměrné výpočty, které v běžné praxi nelze provádět, je nutné provést validaci těchto vztahů. Pro validaci byl použit předcházející model konstrukce zobrazený na obrázku č. 1, u kterého byla změněna hloubka uložení zasklívací jednotky na 18 mm, tepelná vodivost rámu na 0,18 W/m²K (tvrdé dřevo) a byly vybrány tři náhodné tepelné vodivosti těla distančního rámečku. Pro každý z modelů byl vypočten příslušný lineární součinitel prostupu tepla zasklívací spáry ve dvourozměrném teplotním poli v programu Flixo dle ČSN EN ISO 10077-2. Informace o modelech a výsledky výpočtů shrnuje následující tabulka č. 3. Příklad prvního výpočtu lineárního součinitele prostupu tepla je zobrazen na obrázku č. 2.

Obrázek č. 3 Výsledky příkladu validace č. 1

Tabulka č. 3 Vstupní parametry validace
č.	Tepelná vodivost `λ` [W/mK]		Hloubka uložení `x` [mm]	`ψ` [W/mK]
č.	Distanční rámeček	Okenní rám	Hloubka uložení `x` [mm]	`ψ` [W/mK]
1	0,8	0,18	18	0,033
2	5	0,18	18	0,047
3	50	0,18	18	0,066

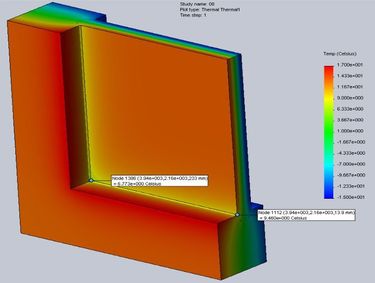
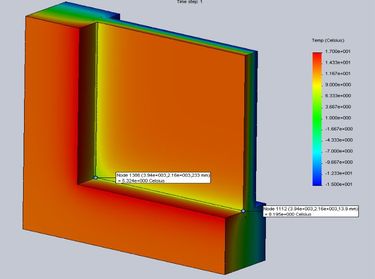
Dále byly pro tyto tři příklady vymodelovány třírozměrné modely rohu rámu, u kterých byly vypočteny vnitřní povrchové teploty v rohu i na charakteristickém průřezu rámu v zasklívací spáře. Grafické výstupy jsou zobrazeny na následujících obrázcích č. 3–5, kde jsou v patřičných místech vyneseny vypočtené povrchové teploty.

Obrázek č. 4 Výsledky příkladu validace č. 2

Obrázek č. 5 výsledky příkladu validace č. 3

S použitím nově odvozené rovnice pro korekční činitel rohu zasklívací spáry γ_ψ byly vypočteny jeho hodnoty.

Příklad č. 1:

γ_ψ = 98,74ψ³ ‧ 10,66ψ² ‧ 0,56ψ ‧ 0,92
γ_ψ = 98,74 ‧ 0,033³ ‧ 10,66 ‧ 0,033² ‧ 0,56 ‧ 0,033 ‧ 0,92
γ_ψ = 0,8935

Příklad č. 2:

γ_ψ = 98,74ψ³ ‧ 10,66ψ² ‧ 0,56ψ ‧ 0,92
γ_ψ = 98,74 ‧ 0,047³ ‧ 10,66 ‧ 0,047² ‧ 0,56 ‧ 0,047 ‧ 0,92
γ_ψ = 0,8804

Příklad č. 3:

γ_ψ = 98,74ψ³ ‧ 10,66ψ² ‧ 0,56ψ ‧ 0,92
γ_ψ = 98,74 ‧ 0,066³ ‧ 10,66 ‧ 0,066² ‧ 0,56 ‧ 0,066 ‧ 0,92
γ_ψ = 0,8650

Výsledky výpočtů ve třírozměrném teplotním poli a výsledky výpočtů z nově zavedené rovnice byly porovnány v následující tabulce č. 4, kde je v přední části uvedeno číslo příkladu, tepelná vodivost těla distančního rámečku a jím tvořený lineární součinitel prostupu tepla zasklívací spáry.

Tabulka č. 4 Výsledky validace odhadu `f`_Rsi-c (porovnání výpočtů 3D a vyvinuté metodiky)
č.	`λ` [W/mK]	`ψ` [W/mK]	Výpočet ve 3D				`γ_ψ` [–]	`f` Rsi-C [–]	Δ `f`_Rsi [–]	Δ `ϑ`_si [°C]
č.	`λ` [W/mK]	`ψ` [W/mK]	`ϑ`_si,min [°C]	`f`_Rsi,min [–]	`ϑ`_si,max [°C]	`f`_Rsi,max [–]	`γ_ψ` [–]	`f` Rsi-C [–]	Δ `f`_Rsi [–]	Δ `ϑ`_si [°C]
1	0,8	0,033	6,773	0,6048	9,460	0,6794	0,8935	0,6071	0,0023	0,081
2	5	0,047	5,324	0,5646	8,195	0,6443	0,8804	0,5672	0,0027	0,096
3	50	0,066	3,485	0,5135	6,475	0,5965	0,8650	0,5160	0,0025	0,091

Výsledkem validace je skutečnost, že u všech tří případů nepřekročila odchylka teplotního faktoru 0,003, resp. povrchové teploty 0,1 °C. V důsledku této malé nepřesnosti, zvláště vezmeme-li v úvahu počet faktorů majících na povrchovou teplotu vliv nebo problematiku přestupových odporů, lze tuto rovnici a korekční činitel rohu zasklívací spáry γ_ψ použít pro teoretický odhad povrchové teploty, resp. teplotního faktoru vnitřního povrchu v rohu zasklívací spáry, a nahradit jím do určité míry složité trojrozměrné výpočty. Je však nutné si uvědomit, že se jedná pouze o matematickoteoretické výpočty, které se v řadě případů mohou od reálných situací lišit.

Závěr

Obrázek č. 6 Ukázka internetová aplikace dostupní na www.decoen.cz/frsi

Článek předkládá nově vyvinutou metodiku pro odhad teplotního faktoru vnitřního povrchu v oblasti zasklívací spáry konkrétně v rohu zasklívací jednotky jako v nejrizikovějším místě vzniku kondenzace vodních par. Metodika je směřována především pro projektanty, stavebníky, developery, výrobce otvorových výplní a v neposlední řadě investory, jako pomoc při volbě konstrukce na základě jednoduchých vstupů. Neslouží pro ověřování požadavku (v současné době doporučení) určeného ČSN 73 0540-2. Byla zároveň vytvořena internetová aplikace volně dostupná na www.decoen.cz/frsi. Ukázka viz obr. č. 6.
Dále:

byl zaveden korekční činitel rohu zasklívací spáry γ_ψ [–] jako bezrozměrné číslo určující závislost mezi teplotním faktorem vnitřního povrchu v zasklívací spáře na charakteristickém průřezu rámu a v rohu zasklívací jednotky;
byla odvozena rovnice pro stanovení korekčního činitele rohu zasklívací spáry v závislosti na lineárním součiniteli prostupu tepla zasklívací spáry jako veličina charakterizující velikost přídavného tepelného toku tvořeného napojením zasklívací jednotky a okenního rámu;

γ_ψ = 98,739ψ³ ‧ 10,662ψ² ‧ 0,555ψ ‧ 0,921
byl stanoven nový vztah teplotního faktoru vnitřního povrchu v zasklívací spáře mezi charakteristickým průřezem rámu a rohem zasklívací jednotky.
f_Rsi-C = γ_ψ ‧ f_Rsi

Ing. Roman Jirák, Ph.D. (*1982) je soudním znalcem v oboru stavebnictví se specializací na otvorové výplně a tepelnou techniku lehkých obvodových plášťů. Absolvoval doktorské studium na ČVUT Fakultě stavební v Praze. Dva roky pracoval jako tepelný technik ve společnosti Skanska v závodě lehkých obvodových plášťů. Poté strávil čtvrt roku na pracovní stáži v IFT Rosenheim v Německu, kde se soustředil na simulaci transportu tepla skrz LOP a otvorové výplně. V současné době řídí společnost DECOEN v.o.s. zaměřující se na tepelnou techniku a na snižování energetické náročnosti budov.

Zdroje

[1] R. JIRÁK, Současné otvorové výplně na českém a evropském trhu II – Nejkritičtější místa z pohledu kondenzace vodních par na vnitřním povrchu, Materiály pro stavbu 3/2013, str. 21–25.
[2] R. JIRÁK, Současné otvorové výplně na českém a evropském trhu VI – Metodika pro odhad teplotního faktoru vnitřního povrchu v oblasti zasklívací spáry, Materiály pro stavbu 6/2013, str. 48–51.

English Synopsis

The methodology for estimation of the thermal factor at the inner surface in the corner of glazing

The surface temperature as one of the most watched parametres of the opening panes and light enveopes not only in the Czech Republic is being assessed in a view of risk of water vapour condensation, or more precisely in a view of their health and a hygyenic flaws and ecologically sound environment where inbuilt. The mening is determination if the structure is suitable for the marginal conditions or whether is necessary to choose another structure.