Analytický model pro stanovení únosnosti a chování kolmého lípnutého tesařského spoje
V tomto příspěvku jsou prezentovány výpočetní modely pro stanovení chování tradičního tesařského lípnutého spoje pomocí analytických vztahů. Základem uváděných výpočetních postupů je metoda komponent, která se běžně využívá při výpočtu ocelových přípojů. Metoda komponent spočívá v rozložení celého spoje na jednotlivé komponenty, které jsou definovány tuhostí dílčích částí spoje. Analytické řešení zahrnuje poklesový efekt dřevní hmoty v blízkosti tlakového zatížení. Výsledky analytického výpočtu jsou srovnávány s experimentálními výstupy. V textu je také popsán normový návrhový postup výpočtu zatížení dřevěného prvku směrem kolmo k vláknům dřeva podle platné evropské normy Eurokód 5 pro názornost a další srovnání.
1. Úvod
Kolmé lípnutí je jedním ze základních příčných tesařských spojů. Lípnutý spoj přenáší tlakové zatížení z končícího konstrukčního prvku do průběžného prvku přes kontaktní plochu obou spojovaných prvků. Obvykle je tento spoj zajišťován proti vybočení tesařskou skobou. Vzhledem k ortotropii dřeva je mezi jeho materiálovými vlastnostmi ve směru rovnoběžně s vlákny a kolmo na vlákna značný rozdíl. Modul pružnosti i únosnost dřeva kolmo k vláknům je nižší než ve směru rovnoběžně s vlákny. Právě díky tomu dochází při tlakovém zatížení horního čela končícího prvku k deformacím průběžného prvku.
2. Experiment
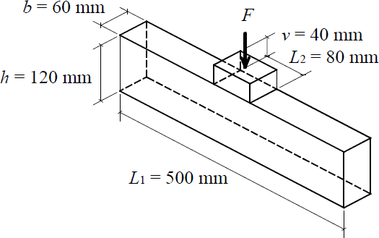
Experimentálnímu testu byla podrobena sada pěti vzorků s délkou vodorovných prvků 500 mm. Geometrické parametry spoje jsou patrné z obrázku 1. Vlhkost všech dřevěných částí byla naměřena mezi 11,2 a 13,1 %. Experiment probíhal při teplotě vzduchu 20,5 °C a byl řízen svislým posunem s rychlostí 1,5 mm/min.
3. Normativní postup
Níže uvedený výpočetní postup podle normy EC5 (ČSN EN 1995–1–1, 2006) stanovuje únosnost dřevěného prvku vystaveného namáhání tlakem kolmo k vláknům. Normový výpočet nezahrnuje velikost deformace, a proto není možné určit závislost působící síly na posunu resp. závislost napětí na poměrném přetvoření. Tato závislost může být vstupem pro přesnější model celé konstrukce, např. dřevěného krovu.
kde je
- σc,90,d
- návrhové napětí v tlaku kolmo k vláknům v účinné kontaktní ploše;
- Fc,90,d
- návrhové zatížení v tlaku kolmo k vláknům;
- Aef
- účinná kontaktní plocha v tlaku kolmo k vláknům;
- fc,90,d
- návrhová pevnost v tlaku kolmo k vláknům, pro konstrukční dřeviny třídy C24 (nejběžnější třída v České republice) podle ČSN EN 338 (2016) – charakteristická hodnota – fc,90,k = 2,5 MPa;
- kc,90
- součinitel zohledňující uspořádání zatížení, možnost štěpení a stupeň deformace v tlaku.
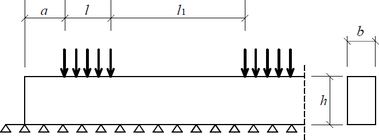
Účinná kontaktní plocha kolmo k vláknům Aef se má stanovit s uvážením účinné kontaktní délky rovnoběžně s vlákny, kde skutečná kontaktní délka l se na každé straně zvětší o 30 mm, avšak ne více než a, l nebo l1/2, viz obrázek 2.
Hodnota kc,90 se má uvažovat 1,0, pokud se nepoužije postup podle následujícího odstavce.
Pro prvky na průběžných podpěrách, za předpokladu, že l1 ≥ 2h, viz obrázek 2, se má hodnota kc,90 uvažovat:
kde h je výška prvku a l je kontaktní délka.
4. Poklesový efekt
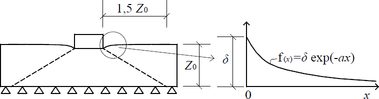
Při stlačování průběžného dřevěného prvku kolmo k jeho vláknům dochází k efektu, který se v mechanice zemin nazývá poklesová kotlina. Tímto jevem se v souvislosti s dřevěnými konstrukcemi zabývali japonští vědci (Kitamori a kol., 2009). Na základě experimentálního výzkumu stanovili logaritmickou funkci f(x), rovnice (3), aproximující poklesovou křivku a odpovídající koeficient a, rovnice (5), který závisí na výšce stlačovaného prvku Z0, jeho uložení a způsobu namáhání. Podílem plochy pod křivkou A(x) ku dráze stlačení δ je možné vypočítat účinnou délku poklesového efektu Lef – rovnice (6). Obrázek 3 zobrazuje důležité parametry pro analytický výpočet včetně vzdálenosti tlakově ovlivněné oblasti a funkci popisující poklesovou křivku.
5. Analytický model
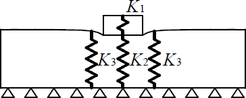
Analytický model spočívá v rozložení jednotlivých částí spoje na dílčí komponenty. Tyto komponenty jsou nahrazeny pružinami a popsány odpovídajícími tuhostmi. Důležitou roli v tomto modelu hraje výše popisovaný poklesový efekt, který zvyšuje celkovou tuhost průběžného prvku.
Tuhosti dílčích komponent jsou definovány následujícími vztahy (geometrické parametry odpovídají obrázku 1):
Průměrné moduly pružnosti pro konstrukční dřeviny třídy C24 podle ČSN EN 338 (2016):
Celková tuhost spoje zohledňující paralelní působení tuhostí K2 a K3 a sériové působení těchto dvou tuhostí s tuhostí K1:
Maximální tlakové zatížení s uvážením normových hodnot návrhové pevnosti v tlaku kolmo k vláknům dřeva fc,90,d a součinitele zohledňující uspořádání zatížení, možnost štěpení a stupeň deformace v tlaku kc,90:
6. Porovnání výsledků
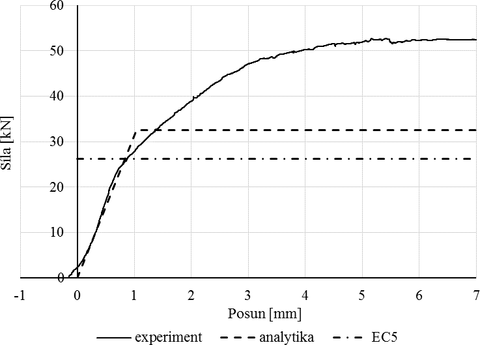
Obrázek 5 zobrazuje křivku průměrných experimentálně zjištěných závislostí síly na posunu, vypočtenou křivku analytickým modelem podle kapitoly 5 a únosnost podle normy EC5 podle kapitoly 3. Ve výpočtech jsou uvažovány charakteristické hodnoty pevností v tlaku kolmo k vláknům dřeva fc,90,k a součinitel kc,90 roven hodnotě 1,25. Skutečná kontaktní délka v případě výpočtu podle EC5 byla na každé straně zvětšena o 30 mm. Výpočet návrhové hodnoty pevnosti v tlaku kolmo k vláknům dřeva fc,90,d zahrnuje součinitel spolehlivost materiálu γM a modifikační součinitel kmod. Modifikační součinitel závisí na použitém konstrukčním materiálu, třídě provozu a délce trvání zatížení.
7. Závěr
V příspěvku je uvedena metodika pro zjištění statického chování a stanovení únosnosti tradičního kolmého lípnutého spoje. Výsledky navrhovaného analytického výpočtu se velmi dobře shodují s experimentální závislostí síly na posunu v její elastické oblasti. Kontaktní délka a tedy i únosnost stanovená analytickým výpočtem je vyšší nežli celková kontaktní délka a únosnost podle normy. Skutečná únosnost spoje z experimentu je vyšší nežli únosnosti vypočtené. Tento fakt je ovlivněn velikostí charakteristické hodnoty pevnosti fc,90,k, která je ve skutečnosti vyšší. Norma uvažuje pouze pevnost pružné oblasti. Model s nelineárním, např. bilineárním, chováním pružin a tlakovou únosností dřeva v plastické části pracovního diagramu materiálové zkoušky by mohl ještě lépe vystihovat skutečné chování spoje.
Přínos do běžné praxe
Spojování nosných prvků hraje významnou roli v návrhu stavebních konstrukcí. Stejně je tomu tak i v případě dřevostaveb. Tuhost spojů má podstatný vliv na průběhy vnitřních sil v konstrukci. Výpočetní statické modely dřevěných konstrukcí s uvážením tuhostí spojů se více přibližují jejich reálnému chování oproti zjednodušeným modelům s kloubovým uložením. Jednoduché analytické vztahy pro stanovení chování a únosnosti spojů jsou stěžejní pro práci projektantů a statiků. Tento článek nabízí příklad návrhového postupu tradičního tesařského kolmého lípnutí. Kolmé lípnutí je nejjednodušším tesařským příčným spojením. Jeho aplikace je vhodná např. pro základové prahy hrázděných budov nebo těžkých dřevěných skeletů. Tento spoj je často prováděn v kombinaci s čepem.
Poděkování
Tato práce vznikla za finanční podpory MŠMT v rámci programu NPU I č. LO1605 – Univerzitní centrum energeticky efektivních budov – Fáze udržitelnosti.
Literatura
- ČSN EN 1995-1-1: Eurokód 5: Navrhování dřevěných konstrukcí – Část 1-1: Obecná pravidla – Společná pravidla a pravidla pro pozemní stavby + Změna A1 + Změna A2. (2006) Český normalizační institut, Praha.
- ČSN EN 338: Konstrukční dřevo – Třídy pevnosti. (2016) Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, Praha.
- Kitamori, A.; Mori, T.; Kataoka, Y. and Komatsu, K. (2009) Effect of Additional Length on Partial Compression Perpendicular to the Grain of Wood. J. Struct. Constr. Eng., 74, 642, pp. 1477–1485.
Autoři článku určili únosnost spoje - kolmé lípnutí jednak pomocí vztahů uvedených v současnosti platné evropské normě pro navrhování dřevěných konstrukcí (ČSN EN 1995-1-1), jednak pomocí inovativního analytického způsobu výpočtu. Tento inovativní způsob spočívá v aplikaci metody komponent, známé z návrhu spojů ocelových konstrukcí. Autoři tuto metodu úspěšně aplikovali na výpočet únosnosti klasického tesařského spoje. Na základě provedených praktických laboratorních testů tesařského spoje autoři prokázali správnost svého postupu a dobrou shodu navrhovaného teoretického řešení metodou komponent s výsledky laboratorních testů. Příspěvek je užitečný i pro projekční praxi, výsledky jsou použitelné.
Computing models for structural behaviour and determination of traditional timber butt joints using analytical relations are presented in this paper. A component method is a base of the computing technique introduced herein. This method is usually used for steel joints design. The component method is based on dividing a joint into individual components. These are defined by partial joint component stiffness. An analytical solution includes a subsidence effect of wooden material in a close proximity of compressive loading. Analytical computation results are compared with the experimental outputs. A design procedure according to Eurocode 5 for a load capacity determination of perpendicularly loaded structural element is stated in the paper.