Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Tepelně technické posouzení detailů kruhových staveb

9.6.2014

Ing. František Vlach

Recenzovaný

Tento článek se pokusí věcně a prakticky poukázat na vliv jednosměrného zakřivení při výpočtech 2D teplotních polí stavebních detailů za účelem výpočtu lineárních činitelů prostupu tepla. Úvodní část se věnuje typologii a příklady staveb s organickým tvaroslovím. Dále jsou uvedeny teoretické předpoklady a analýza výpočtu lineárních činitelů prostupu tepla. Na výsledných závislostech lze vypozorovat poloměry, při nichž se vliv zakřivení technicky významně projeví.

Úvod

Současné stavebnictví je orientováno na stavby s nízkou energetickou náročností. Kromě aplikace obecných návrhových principů energeticky úsporné architektury je kladen důraz na použití přesných návrhových výpočetních postupů. Jedná se především o metodiky určení energetické náročnosti objektu jako celku. Významnými parametry vstupujícími do tohoto výpočtu jsou charakteristiky obálky budovy. Pro jejich stanovení jsou používány již vypracované metodiky.

V tomto článku je demonstrován vliv zvolených souřadnic výpočtu lineárního činitele prostupu tepla. Výpočet tohoto parametru je obvykle založen na řešení 2D teplotního pole pomocí počítačových simulací FEM. V projekční praxi rozšířené výpočetní nástroje ovšem obvykle pracují pouze v kartézském souřadnicovém systému. Pro řešení konstrukčních částí staveb jedenkrát zakřivených je potřebné řešit úlohu v geometrii uplatňující cylindrické souřadnice. Na obrázku 1 je uveden vysvětlující demonstrativní snímek stavby, u kterých je daný problém možné řešit.

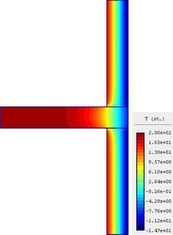
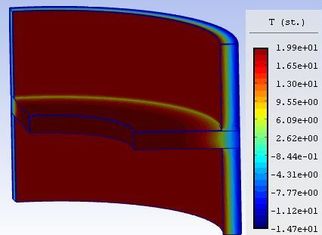
Obrázek 1: Termografický snímek stavby se zakřivenou konstrukční částí obálky budovy s viditelnou tepelnou vazbou v tomto místě. [1]

Příklady staveb se zakřivenou fasádou

Je zřejmé, že řada čtenářů bude namítat, že se tento druh plošných konstrukcí nevyskytuje v hojné míře. Proto věnujme úvodní část textu příkladům typologicky předmětných staveb.

S organickými tvary u staveb se ve skutečnosti setkáváme poměrně často, aniž bychom si to výrazně uvědomovali. A nemusí jít jen o ojedinělé architektonické experimenty. Obzvláště stávající stavební fond vzniklý v první polovině 20. století je velmi hojně doplňován o části fasád kruhově zakřivených. Vedle těchto individuálních projektů funkcionalismu jsou naše města plná těchto objektu doslova na každém rohu. Právě řešení nároží uličních front často uvažuje se zakřivením obálky budovy.

Po provedené individuální analýze stavebního fondu vybraných lokalit ČR z mapových podkladů je zřejmé, že obdobných staveb se vyskytuje nad očekávání velké množství. Jde především o stavby s kruhovým tvarem stěn či střechy. Při přípravě tohoto článku byly zaznamenány stavby s poloměry zakřivení stěn do 300 m. Zakřivení stěn zdola není omezeno a z hlediska četnosti výskytu je mnohem častější. Vyskytují se stavby jak konkávního, tak i konvexního tvaru zakřivené plochy.

S ohledem na četný výskyt budov s jedenkrát zakřiveným rozměrem obvodového pláště je vhodné, aby byla stanovena míra přesnosti při zanedbání křivočarosti řešeného detailu.

Uvedené příklady s obrazovým doprovodem jsou z různých lokalit města Brna a snaží se reprezentovat stavby objemné a s velkými poloměry či četnými lineárními vazbami zakřivených detailů. Co do tvarosloví jednotlivých stavebních typů jsou obdobné příklady dostupné v řadě dalších obcí. Pro ilustraci jsou doplněny snímky aplikace umožňující náhled do katastrálních map s vyznačením orientačních poloměrů apod.

Obrázek 2: Polyfunkční objekt Sfinx v Brně obsahuje jak konvexní, tak konkávní tvary. Obdobný příklad lze nalézt v Ostravě v podobě stavby Atria Slezská. Na tomto snímku je patrné, že nejen půdorysné zakřivení v rámci obvodových stěn, nýbrž válcové střechy jsou rovněž předmětem smyslu tohoto článku. Výskyt válcových stěn je rovněž hojný. [1]

Obrázek 3: Takzvaný „brněnský rohlík“ na snímku z katastrální mapy [2] a z jeho konkávně zakřivené fasády [1]. Obdobně řešené jsou z kruhového Vaňkova náměstí z dílny architekta Jindřicha Kumpošta nebo objekty při ulici Jubilejní v Ostravě, objekt při ulici Pod klaudiánkou v Praze a řada dalších.

Obrázek 4: V oboru velkých moderních staveb uveďme novou scénu Městského divadla v Brně, výškovou budovu M Paláce, a různá sportoviště či víceúčelové haly typu haly Rondo či O₂ arény v Praze. Tyto velkorozponové haly uvádíme pro jednoznačnou demonstraci a představu o poloměrech a zakřiveních, se kterými se můžeme u nás setkat. [2]

Obrázek 5: Pasivní kruhový dům v Rapoticích [1]

Mohli bychom uvést řadu dalších příkladů s obrazovým doprovodem, avšak toto není hlavním předmětem článku. Vhodným nástrojem pro získání dalších příkladů je pro aktivního čtenáře, z internetu dostupná, letecká mapa. Na příklady narazíme nejen u nás, ale u všech našich sousedů, v Rusku i USA.

Předmětem našeho zájmu jsou však především stavby, které se snaží minimalizovat tepelné ztráty obálkou budovy. Jako jeden příklad za mnohé uveďme pasivní kruhový dům v Rapoticích na obrázku 5. Další stavbou tohoto druhu je například mediálně známý Dům stromů.

Výpočet

Předmětem článku je stanovení lineárního činitele prostupu tepla u detailu stavební konstrukce. Lineární činitel prostupu tepla charakterizuje tepelně technické vlastnosti dvourozměrných tepelných mostů a vazeb. Vyjadřuje množství tepla ve W, které prochází při jednotkovém teplotním rozdílu jednotkovou délkou tepelného mostu. Obecně se stanoví vztahem:

(1)

Při řešení úlohy, která je předmětem tohoto článku, bylo provedeno srovnání výpočtu modelu v kartézském a cylindrickém systému. Pro tento účel byly zvoleny jednoduché tepelné vazby uložení stropu na stěně ve dvou variantách skladeb. Tento výpočet byl proveden pro konvexní i konkávní případ.

Teplotní pole je obecně popsáno diferenciální rovnici:

(2)

V případě osově symetrického uspořádání řešeného konstrukčního prvku platí přepis Fourierovy diferenciální rovnice vedení tepla v cylindrických souřadnicích:

, (3)

kde je

r: – poloměr zakřivení.

Aby bylo možno řešit úlohu 2D teplotního pole osově symetrického uspořádání, musí být použit software, který v příslušných souřadnicích umí pracovat. Dvojdimenzionální řešení teplotního pole předpokládá volbu řezu typické skladby detailu a tento je lineárně aplikován na 1 m délky. V případě zakřivení po kružnici je poměr vnějších a vnitřních ploch, kterými do detailu vstupuje a vystupuje teplo, odlišný. Samo zakřivení tedy způsobuje deformaci teplotního pole oproti navazujícím plošným rovinným stěnám.

Zvolený příklad obecně simuluje uložení homogenní stropní desky na obvodovém zdivu v různém smyslu zakřivení. Podstatné informace ukazuje obrázek 6.

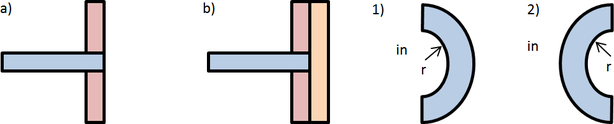
Obrázek 6: Geometrie řešeného detailu: a) jednovrstvé zdivo, b) dvouvrstvé zdivo s řešeným tepelným mostem, 1) konkávní půdorysné uspořádání, 2) konvexní půdorysné uspořádání, r poloměr.

Poloměr r je pro daný účel v jednotlivých krocích a případech výpočtu volen v kroku:
1;2;3;4;5;8;10;15;20;25;30;35;40;45;50;55;60;65;70;75;80;100;150;200;250;300;350;400;450;500;600;1000 m. Podmínky a přesnost výpočtu jsou v souladu s ISO 10211.

Obvyklá přesnost vypočtených hodnot lineárního činitele prostupu tepla je udávána na tři desetinná místa. V tomto článku je hodnocení vztaženo na přesnost udaných hodnot o řád vyšší.

Diskuze výsledků

Výsledky analýzy ukazují vliv zvoleného souřadného systému na hodnotu lineárního činitele prostupu tepla. Na základě získaných výsledků byly pro jednotlivé řešené případy sestaveny závislosti, ze kterých je zřejmý vliv poloměru na výsledek.

Obrázek 7: Teplotní pole řešeného detailu v řezu a při respektování rotačního systému.

Graf na obrázku 8 ukazuje závislost lineárního činitele prostupu tepla na poloměru zakřivení v konvexní a konkávní variantě neizolovaného detailu. S rostoucím poloměrem zakřivení se hodnota blíží výsledku, který lze získat standardním řešením. Významných rozdílů je dosaženo při poloměrech do r = 100 m.

Graf na obrázku 9 ukazuje závislost lineárního činitele prostupu tepla na poloměru zakřivení v konvexní a konkávní variantě izolovaného detailu. I v případě menšího vlivu tepelné vazby je zakřivení detailu významné do poloměru r = 100 m.

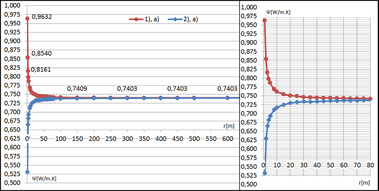
Obrázek 8: Závislost lineárního činitele prostupu tepla na poloměru zakřivení v konvexní a konkávní variantě neizolovaného detailu.

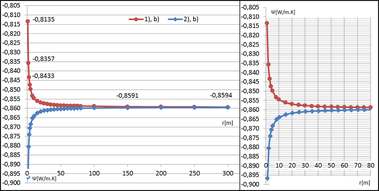
Obrázek 9: Závislost lineárního činitele prostupu tepla na poloměru zakřivení v konvexní a konkávní variantě izolovaného detailu.

Oba případy ukazují, že maximální odchylka při zanedbání křivosti řešeného detailu se může pohybovat ve významném řádu. Konkrétně pro případ a) byl získán rozdíl Δ = 0,21 a pro případ b) Δ = 0,05.

Závěr

Řešení lineárních činitelů prostupu tepla je v projekční praxi významnou úlohou, která má vliv na přesnost dalších výpočtů. Stavby s kruhovými tvary jsou v současnosti rozšířené. Používané poloměry zakřivení nejčastěji nabývají hodnot do 100 m. Uvedenou analýzou byl prokázán vliv na výslednou hodnotu lineárního činitele prostupu tepla právě při zakřivení v těchto poloměrech. Přínosem tohoto článku pro praxi je informace o míře možné odchylky od přesného řešení, bude-li použito výpočtu v kartézských souřadnicích.

Očekávaný efekt se projevuje více u nižších poloměrů, což vede k závěru, že obzvláště u objektů s velkou délkou tepelné vazby nebo u částí objektů s významným zakřivením je dobré tuto tvarovou skutečnost zohlednit. Ovšem vždy jen v případě, když chceme deklarovat výpočet za použití přesných hodnot lineárních činitelů prostupu tepla. V případě použití tabulkových paušálních přirážek to není předmětné.

Zakřivení stěnových ploch je i otázkou řešení výpočtu součinitele prostupu tepla. Tento postup je znám a běžně se užívá pro výpočty potrubních vedení rozvodů chladu či tepla.

Vedle jednosměrně zakřivených detailů lze hovořit o kulových plochách a tedy sférických souřadnicích. Jejich výskyt je však ojedinělý.

Poděkování

Tento příspěvek vznikl za podpory projektu FAST-J-14-2322 na Fakultě stavební VUT v Brně.

Literatura

[1] Archiv společnosti Gades solution s.r.o. a Tee-pee.cz
[2] Nahlížení do katastru nemovitostí. ČESKÝ ÚŘAD ZEMĚMĚŘICKÝ A KATASTRÁLNÍ. Nahlížení do katastru nemovitostí [online]. [cit. 2014-03-29]. Dostupné z: http://nahlizenidokn.cuzk.cz/
[3] Karban, P., Mach, F., Kůs, P., Pánek, D., Doležel, I.: Numerical solution of coupled problems using code Agros2D, Computing, 2013, Volume 95, Issue 1 Supplement, 381–408.
[4] Vaverka, J.: Stavební tepelná technika a energetika budov. Brno: VUTIUM, 2006. 642 s.
[5] ČSN EN ISO 10211-2 (73 0551). Tepelné mosty ve stavebních konstrukcích – Tepelné toky a povrchové teploty – Podrobné výpočty, Praha: Český normalizační institut, 2009.
[6] ČSN 3 0540–4. Tepelná ochrana budov. Část 4: Výpočtové metody, Praha: Český normalizační institut, 2007

English Synopsis

Thermal protection of curved building detail

This paper deals with the determination of linear thermal transmittance for buildings with rounded shapes. Introduction deals with typlogy and examples of the buildings containing organic shape. Subsequently is described the theory of determination of linear thermal transmittance. It provides information applicable for buildings assessment in engineering practice.