Činitel jasu a činitel odrazu světla ve výpočtech denního osvětlení
Při výpočtech denního osvětlení budov se vlastnosti stínících překážek vyjadřují buď pomocí činitele jasu nebo pomocí činitele odrazu světla. Článek informuje o vztahu mezi těmito dvěma činiteli a nabízí program JAFAS 2024 k výpočtu průměrného činitele jasu v jednoduché urbanistické situaci.
1. Přesnost výpočtů denního osvětlení
Obloha se považuje za plošný zdroj světla se sluncem jako zdrojem téměř bodovým. Intenzita denního světla i rozložení jasu na obloze se během dne i roku mění. Tyto změny probíhají v závislosti na počasí naprosto nepravidelně a nahodile s dynamikou, která neumožňuje ani přibližnou předpověď stavu tohoto zdroje v nejbližších minutách. Jedinou naší jistotou je střídání dne a noci. Aby bylo možné alespoň něco stálého hodnotit, byla jako kritérium zavedena poměrná veličina – činitel denní osvětlenosti D [%]. Jedná se o poměr osvětlenosti E [lx] v hodnoceném místě k současné osvětlenosti EH [lx] nestíněné vodorovné roviny osvětlené celou oblohou.
(1)
I tento činitel by byl pod skutečnou oblohou neuchopitelně proměnlivý v čase. Proto hodnocení probíhá při stavu zatažené oblohy v zimě s modelovým rozložením jasu L [cd.m−2] podle vztahu
kde Lm [cd.m−2] je průměrný jas oblohy a q [–] je činitel gradovaného jasu oblohy. Pro mezinárodní standard zatažené oblohy CIE 1:3, který předpokládají naše a evropské technické normy [1] [2], se hodnota tohoto činitele stanoví v závislosti na výškovém úhlu γ [°] nad obzorem podle vztahu
(3)
Zatažená obloha je v zimním období z hlediska množství světla nejméně příznivou možnou situací. Posouzení vychází z logického předpokladu, že pokud je dostatek denního světla při této nejméně příznivé obloze, pak bude dost světla i při jakékoli obloze jiné. Je nutno poznamenat, že tato úvaha je správná jen pro množství světla. Kvalita osvětlení je často nejvíce zhoršena při jiných stavech oblohy, zejména při přímém slunečním světle. Osvětlenost nestíněné vodorovné roviny se stanoví integrací.
(4)
Nestálost oblohy jako zdroje světla je příčinou relativně nízké přesnosti in situ měření činitele denní osvětlenosti. V porovnání s deklarovanou přesností výpočtů, které se provozují na počítačích, je přesnost měření řádově nižší. Tato skutečnost a velká závislost měření na počasí jsou příčinou toho, proč se ve stavební praxi úroveň denního osvětlení prokazuje téměř výhradně výpočtem, zatímco měření se provádí spíše výjimečně. Nutno ale poznamenat, že i tak málo přesným měřením je možno dostatečně spolehlivě odhalit velké, a tedy na zdraví a pohodu lidí skutečně negativně působící, nedostatky. Měření dostatečně přesné pro účely výzkumu a pro testování softwarů lze provádět jen v laboratorních podmínkách na modelu pod umělou oblohou.
2. Geometrické vlastnosti stínících překážek
Výpočtem denního osvětlení se ověřuje správnost rozměrů budov, proporcí místností, velikost oken a dostatečnost vzájemných odstupů mezi budovami. Proto nelze rozměry a odstupy stínících překážek při posuzování zjednodušovat nebo jinak měnit. Není to ani třeba. Rozměry budovy jsou zpravidla dobře známy z projektové dokumentace a rozměry jejího okolí z geodetického zaměření. Údaje jsou dostatečně přesné a lze je považovat za neměnné a trvající až do budoucí přestavby domu, kdy ale bude nutno znovu vypracovat projekt s novým posouzením denního osvětlení rekonstruovaného domu i domů novou stavbou stíněných.
3. Světelně technické vlastnosti stínících překážek
Rozměr není jedinou vlastností stínící překážky. Důležité jsou i její světelně technické vlastnosti. Činitel odrazu světla ρ [–] závisí na barevném odstínu povrchu stínící překážky a má vliv na její jas L [cd.m−2] podle vztahu
(5)
kde E [lx] je osvětlenost daného místa. Osvětlenost je způsobena nejen světlem oblohy, ale i světlem odraženým od ostatních objektů v dané urbanistické situaci a světlem odraženým od terénu. Výpočtem na PC je možné vzájemnou světelnou interakci mezi oblohou, budovami a terénem přibližně modelovat. Přibližně proto, že přesnost výpočtu závisí na velikosti a počtu dílčích ploch, na které jsou stínící překážky a terén pro výpočet rozděleny. S jejich vzrůstajícím počtem narůstá čas zpracování výpočtu a počet těchto ploch je také limitován kapacitou procesoru počítače.
Obr. 1: Barevné řešení domů v roce 2001 a po rekonstrukci v roce 2017
Obr. 2: Jas průčelí ovlivněný architektonickými prvky fasády
Činitel odrazu světla ρ [–] ale vůbec není nic stálého. Navíc je bohužel tato veličina někdy do výpočtů světelných interakcí dosazována spekulativně v hodnotách, které neodpovídají realitě. Barva průčelí budov se v čase mění důsledkem působení atmosférických vlivů a vlivem zaprášení. Zcela změnit se může novým nátěrem – viz obrázek 1. Při realizaci nového nátěru úřady zpravidla nevyžadují nové světelně technické posouzení.
Jas průčelí je pod římsami a balkóny snížen stíněním a v závislosti na reliéfu fasády podléhá změnám i při jednotné barvě nátěru – viz obr. 2. Na obrázku lze rovněž pozorovat, že odstín barvy oken, a tedy i jejich činitel odrazu světla ρ [–], je ovlivněn odrazem oblohy v těchto oknech a má proto z každého směru pohledu jinou hodnotu. Okna nemusí být vždy černá, jak se dosud při výpočtech předpokládalo.
4. Jednoznačnost výpočtů denního osvětlení
Zatímco rozměry stínících překážek lze vždy přesně ověřit, jejich světelně technické vlastnosti jsou v čase proměnné a jejich přesné stanovení je vždy obtížné a často nejisté. To je vodou na mlýn odpůrcům správních rozhodnutí a stěžovatelům, kterým taková nejistota poskytuje argumenty pro zpochybnění světelně technických výpočtů a tím i celého posouzení novostavby. Vzájemné stínění je totiž častým námětem sporů, které jsou řešeny stavebními úřady a soudy. Při absenci jednoznačného způsobu stanovení činitelů odrazu světla stínících překážek je nalezení spravedlnosti při takových sporech obtížné. České technické normy tomuto problému čelily tím, že předepsaly pro všechny stínící překážky a pro terén jednotnou hodnotu činitele jasu k = 0,1. Znamená to, že jas L [cd.m−2] stínící překážky nebo terénu se rovná jedné desetině průměrného jasu Lm [cd.m−2] oblohy.
(6)
Výhodou tohoto způsobu byla možnost kontroly výsledku mimo počítač některou z tradičních grafických metod. V naší republice se nejvíce používala Daniljukova metoda [3] nebo Kittlerovy protraktory [4]. Přizpůsobení výpočtu k jasu stínících překážek se provádělo pouhým násobením hodnotou k = 0,1. Jasová interakce mezi objekty, kterou předpokládá evropská norma [2], vnesla do výpočtu komplikaci, kterou grafickopočetní metody už nezvládnou. Dnes se výpočty činitele denní osvětlenosti provádějí téměř výhradně pomocí specializovaných softwarů na osobních počítačích a na grafickopočetní metody si už málo kdo vzpomene. Jsou však dosud jediným prostředkem srozumitelné kontroly výsledku výpočtu na PC. Taková kontrola bude vždy potřebná, protože algoritmy jsou známy jen autorům softwaru a vstupní hodnoty použité ve výpočtu zná často jen operátor.
Evropská norma [2] s činitelem jasu nepracuje, ale předpokládá výpočet světelné interakce mezi objekty a terénem v zadané urbanistické situaci. Do takového výpočtu se zadávají činitelé odrazu světla ρ [–] stínících překážek a terénu. Pro terén norma [2] stanovuje průměrnou hodnotu ρt = 0,2 a pro stínící překážky (venkovní stěny) připouští hodnoty v rozmezí 0,2 až 0,4. Česká normalizace [5] se zatím kloní k jednoznačné hodnotě ρp = 0,3. Jedná se o průměrnou hodnotu včetně oken, obkladů, oplechování a dalších fasádních prvků. Důsledné používání hodnot ρt = 0,2 a ρp = 0,3 ve výpočtech zajistí potřebnou jednoznačnost a nezpochybnitelnost posouzení denního světla. Uživatelům grafických pomůcek a starších verzí programů WAL a SVĚTLO+ lze doporučit používání činitele jasu k = 0,1 podle dosavadních zvyklostí. Chyba takového postupu nemusí být velká v případech, kdy významnou roli hraje oblohová složka činitele denní osvětlenosti. Přímé světlo z oblohy není ovlivněno jasem terénu ani stínících překážek a často řádově dominuje nad světlem odraženým.
5. Použití vztahů fotometrie
Ke kontrole výpočtů provedených počítačem někdy postačí základní vztahy fotometrie. S využitím vztahů (4) a (5) lze stanovit závislost mezi činitelem jasu k [–] a činitelem denní osvětlenosti d [–]. Pro činitel denní osvětlenosti, který je vyjádřený jako desetinné číslo (tedy nikoli v %), je použito označení s malým písmenem d [–].
Ze vztahu (7) vyplývá, pro činitel jasu nestíněné vodorovné roviny
Pro svislou rovinu osvětlenou jen světlem oblohy CIE 1:3 platí
,
(9)
zatímco při osvětlení jen oblohou s konstantním jasem by měla svislá rovina činitel jasu
6. Program JAFAS
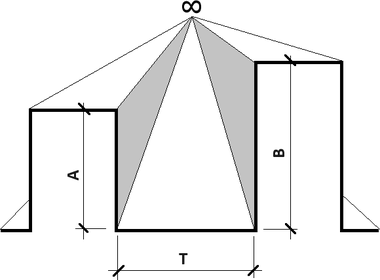
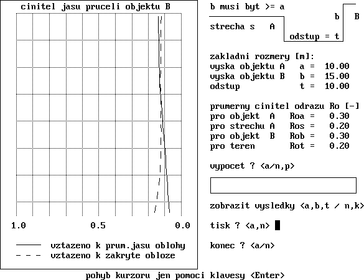
V devadesátých letech minulého století autor tohoto článku sestavil ve vývojovém prostředí Power Basic program JAFAS, kterým bylo možné formou grafu stanovit průběh hodnot činitele jasu po výšce fasády v urbanistické situaci, která byla tvořena dvěma proti sobě stojícími dlouhými řadami domů („nekonečná“ ulice) – viz obrázek 3. Ukázka výstupu programu JAFAS je na obrázku 4. Tento program pracoval v operačním systému DOS a není proto na dnešních počítačích běžně použitelný.
Obr. 3: „Nekonečná“ ulice
Obr. 4: Ukázka výstupu z programu JAFAS
Obr. 5: Ukázka programu JAFAS 2024
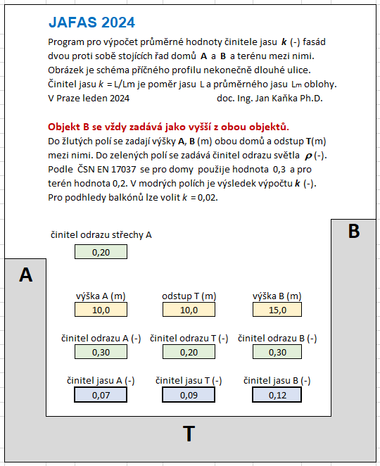
Aktuálně autor tohoto článku nabízí program JAFAS 2024, který využívá radiační metodu výpočtu a pracuje v prostředí Excel. Jedná se opět o urbanistickou situaci tvořenou „nekonečnou“ ulicí. Zadává se výška A a B [m] proti sobě stojících objektů a odstup T [m] mezi nimi v rozsahu hodnot od 0,1 do 100 m a hodnoty činitelů odrazu světla ρ [–] obou fasád, terénu a ploché střechy jednoho z objektů v rozsahu hodnot 0,01 až 0,99. Výsledkem výpočtu jsou průměrné hodnoty činitele jasu k [–] obou fasád a terénu mezi objekty. Nejpřesnější výsledek výpočtu činitele denní osvětlenosti poskytují specializované softwary. Program JAFAS 2024 nemůže tuto přesnost nahradit, ale poskytuje grafickému řešení větší míru přesnosti v porovnání s použitím jen hodnoty k = 0,1. Výsledek bude většinou na straně bezpečnosti posouzení, neboť se posuzuje „nekonečná“ ulice, zatímco v reálných urbanistických situacích jsou objekty konečné. Tak lze doufat, že činitel jasu bude oproti výsledku výpočtu reálně navýšen světlem, které přichází po stranách objektů. Ukázka výstupu je na obrázku 5. Program lze zdarma zkopírovat na adrese www.svetloplus.cz/?p=news.
Literatura
- ČSN 730580-1 Denní osvětlení budov – základní požadavky (2007)
- ČSN EN 17037 Denní osvětlení budov (2018)
- KAŇKA, J. Inovovaný způsob použití Daniljukovy metody, Světlo, 2011, (14)4, 44-46
- KITTLER, R. – KITTLEROVÁ, L. Návrh a hodnotenie denného osvetlenia, Bratislava: Alfa, 1975
- ČSN 730582 Denní osvětlení budov – doplňující požadavky (v návrhu)
When calculating the daylighting of buildings, the properties of shading obstacles are expressed either by means of a brightness factor or by means of a light reflection factor. The article reports on the relationship between these two factors and offers the JAFAS 2024 program to calculate the brightness factor in a simple urban situation.
