Vybrané grafické metody zjišťování činitele denní osvětlenosti (2. část)
Článek se zabývá popisem vybraných graficko-početních metod sloužících ke stanovení množství denního světla. Je vysvětlen princip odvození těchto metod a popsán princip práce s příslušnými diagramy. V současné době se zřídka setkáváme s používáním diagramů v praxi, ale některé odborné softwary je využívají buď přímo, nebo alespoň ve svých grafických výstupech.
4. Waldramův diagram
Nevýhodou Daniljukovy metody je její omezení jen na posuzování navzájem rovnoběžných objektů jakoby domů v dlouhé ulici, teoreticky nekonečně dlouhé. Po společenské změně v devadesátých letech minulého století se výstavba přesunula do center měst, často do vnitrobloků obytných domů, kde posuzování Daniljukovou metodou z důvodu složitosti zástavby začalo selhávat. Vhodnou metodou pro tyto podmínky je Waldramův diagram [11]. Na Slovensku se o této metodě zmiňuje literatura [12]. Waldramův diagram je takové zobrazení okolí posuzovaného místa, kde plocha zobrazení je úměrná činiteli denní osvětlenosti. Na obrázku je diagram opatřen čtvercovou sítí, kde plocha každého čtverce odpovídá hodnotě D = 0,1 %.
Výhodou Waldramova diagramu je názornost a zejména možnost posuzovat vliv stínění překážkami i složitých tvarů. Je-li stínící překážka různoběžná s oknem nebo mění-li složitě svůj tvar a výšku, pak je Waldramův diagram vhodnou graficko-početní metodou pro stanovení hodnot činitele denní osvětlenosti.
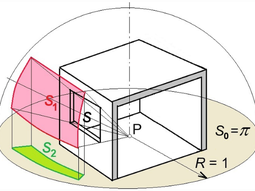
Jedná se o pravoúhlý diagram, kde úsečkou je azimut a pořadnicí funkce elevačního úhlu ε (°). Tato funkce bude v následujícím textu odvozena. Rozměry v diagramu mají dva významy, první je prezentován horizontální stupnicí azimutů, která je lineární v rozsahu (−π⁄2, +π⁄2) a svislou stupnicí elevačních úhlů, která je v rozsahu (0, +π⁄2) a je nelineární – uzpůsobená tak, aby byla splněna požadovaná vlastnost Waldramova diagramu: plocha zobrazení plošného zdroje světla má být úměrná osvětlenosti, kterou tento zdroj vyvolá v posuzovaném bodě. Druhým významem jsou délkové rozměry (ve směru úsečky a ve směru pořadnice) při zjišťování plošného obsahu zobrazení v diagramu. Podle obrázku 8 se bude sledovat osvětlenost v bodě M, který leží na vodorovné rovině. Jas plošného zdroje světla je konstantní a zdroj světla má tvar obdélníka, který leží ve svislé rovině. Lze si představit velmi úzké okno šířky š (m) s parapetem v úrovni osvětlované roviny. Pravé a levé ostění okna vymezují elementární rozdíl azimutů dA (°). Výškou okna je vymezen elevační úhel ε1 (°). Cílem je stanovit, jak se bude měnit osvětlenost v bodě M v závislosti na výšce okna, tedy v závislosti na hodnotě elevačního úhlu ε1 (°).
![Obrázek 7: Waldramův diagram (podle [12])](/docu/clanky/0263/026344o1.jpg)
Obrázek 7: Waldramův diagram (podle [12])
![Obrázek 8: Schéma k odvození Waldramova diagramu – axonometrie (podle [16])](/docu/clanky/0263/026344o3.png)
Obrázek 8: Schéma k odvození Waldramova diagramu – axonometrie (podle [16])
![Obrázek 9: Schéma k odvození Waldramova diagramu – půdorys a řez (podle [16])](/docu/clanky/0263/026344o5.png)
Obrázek 9: Schéma k odvození Waldramova diagramu – půdorys a řez (podle [16])
Okno podle obrázků 8 a 9 se rozdělí po výšce na větší počet elementárních ploch. S využitím vztahu (8) je činitel denní osvětlenosti způsobený j-tou plochou
.
(39)
Z geometrického uspořádání podle obrázku 9 vyplývá, že
.
(40)
Hodnota činitele denní osvětlenosti způsobená celým oknem se stanoví dosazením vztahu (40) do (39) a jeho následnou integrací.
(41)
![Obrázek 10: Návrh Waldramova diagramu (podle [16])](/docu/clanky/0263/026344o10.png)
Obrázek 10: Návrh Waldramova diagramu (podle [16])
Libovolnou volbou šířky Z (m) a výšky H (m) diagramu se stanoví jeho velikost. Stupnice na ose úseček má rozsah od −π/2 do +π/2, tedy Z = π. Diagramem je zobrazena právě jedna polovina oblohy. Jeho plocha Z ‧ H = π ‧ H je proto úměrná činiteli osvětlenosti D = 50 %.
Sledovaný plošný zdroj světla tvaru vysokého svislého obdélníka se v diagramu zobrazí jako obdélník šířky dA. Jeho výška y (m) je hledanou pořadnicí diagramu. Plocha tohoto obdélníka však musí být úměrná činiteli osvětlenosti podle vztahu (41). Lze sestavit úměrnost
(42)
Úpravou rovnice (42) se získá vztah pro výpočet pořadnice y (m)
(43)
![Obrázek 11: Upravený Waldramův diagram (podle [13])](/docu/clanky/0263/026344o14.png)
Obrázek 11: Upravený Waldramův diagram (podle [13])
Původní Waldramův diagram předpokládal konstantní jas oblohy. Nevychází z výpočtového modelu zatažené oblohy s gradovaným jasem a neuvažuje směrový prostup světla zasklením okna. Tyto vlivy byly do metody zahrnuty až při úpravě Waldramova diagramu, kterou začátkem 90. let minulého století provedl Kaňka [13].
Plocha čtverce v levém horním rohu na diagramu z obrázku 11 odpovídá hodnotě D = 1,0 % a určuje tak měřítko diagramu. Odvození pořadnice y (m) tohoto diagramu je v principu stejné jako u původního Waldramova diagramu, jen vztahy jsou poněkud složitější.
(44)
(45)
kde
(46)
(47)
Od roku 2007 byl v naší technické normalizaci [14] zaveden činitel denní osvětlenosti Dw (%) roviny zasklení okna jako kritérium zastínění existujících budov novostavbami. Okna budov jsou většinou ve svislém průčelí, a tak v souvislosti s tímto kritériem nabyl na významu Waldramův diagram pro osvětlení svislé roviny v exteriéru [15].
![Obrázek 12: Waldramův diagram pro osvětlení svislé roviny (podle [16])](/docu/clanky/0263/026344o20.png)
Obrázek 12: Waldramův diagram pro osvětlení svislé roviny (podle [16])
Odvození pořadnice y (m) tohoto diagramu je opět v principu stejné jako u původního Waldramova diagramu. Činitel denní osvětlenosti svislé roviny v exteriéru se stanoví integrací.
(48)
a pořadnice diagramu vychází
(49)
4.1 Princip práce s W-diagramem upraveným pro svislý osvětlovací otvor
Upravený Waldramův diagram popsaný výše je nutné konstruovat v závislosti na sklonu osvětlovacího otvoru, sklonu srovnávací roviny a uvažovaném terénu. Pro účely běžné praxe je postačující diagram znázorněný na obr. 11, který lze použít pouze pro
- svislý osvětlovací otvor,
- vodorovnou srovnávací rovinu,
- tmavý terén s gradací jasu oblohy 1:3.
Stejně jako Daniljukovy úhlové sítě, slouží i Waldramův diagram pro určení oblohové a vnější odražené složky činitele denní osvětlenosti. Pro určení oblohové složky platí vztah
(50)
a pro určení vnější odražené složky vztah
(51)
Význam dílčích veličin v obou vztazích je shrnut v tabulce 3. Hodnoty obou složek se opět uvádějí v procentech s přesností na jedno desetinné místo.
| Označení a název dílčí veličiny | Výpočet dílčí veličiny | |
|---|---|---|
| Ps (mm2) * | plocha, kterou v diagramu zaujímá obloha | vymezení plochy pomocí upraveného Waldramova diagramu |
| Pe (mm2) | plocha, kterou v diagramu zaujímá stínící překážka | |
| P0 (mm2) | plocha čtverce (obdélníku **) v levém horním rohu diagramu | |
| τ0,nor (–) | souhrnný činitel prostupu světla ve směru normály | viz (29), dílčí veličiny viz tabulka 1 |
| kγ (–) | činitel jasu stínící překážky | viz (23), obvykle kγ = 0,1 |
| Poznámky k tabulce 3: * Lze použít i jinou plošnou jednotku. Je však třeba, aby obě veličiny, které vyjadřují poměr (Ps / P0 , Pe / P0) byly ve shodných jednotkách. ** Výhodou diagramu je, že použití není ovlivněno konkrétním poměrem stran diagramu. Například dojde-li při tisku k jednostranné deformaci diagramu, zdeformuje se i jednotkový čtverec v levém horním rohu diagramu (stane se z něj obdélník). Díky poměru dvou ploch stejně zdeformovaných se docílí správného výsledku. | ||
V diagramu znázorněném na obrázku 11 slouží křivky znázorněné plnou čarou (odstupňované po 5°) k zakreslení parapetu a nadpraží osvětlovacího otvoru a k zakreslení vodorovných částí stínícího objektu, které jsou rovnoběžné s rovinou osvětlovacího otvoru. Křivky znázorněné přerušovanou čarou slouží k zakreslení vodorovných částí stínícího objektu, které jsou kolmé na rovinu osvětlovacího otvoru. Svislé hrany se v diagramu zakreslí jako kolmice na hlavní osu diagramu. U složitějších tvarů stínících objektů se nejprve zakreslí vrcholy jednotlivých hran, které se následně spojí plynulou čarou. Princip zakreslení objektů v upraveném Waldramově diagramu je patrný z obrázku 15.
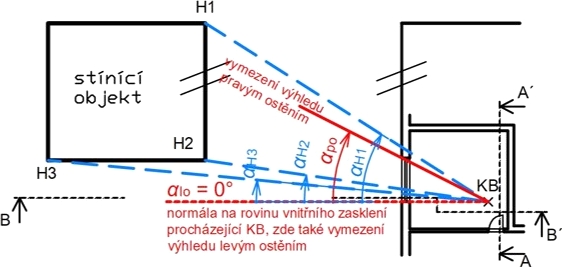
Obrázek 13: Princip práce s Wladramovým diagramem – vstupní údaje zjištěné z půdorysu
Obrázek 14: Princip práce s Waldramovým diagramem – vstupní údaje zjištěné ze svislého řezu B-B´ (vlevo) a A-A´ (vpravo)
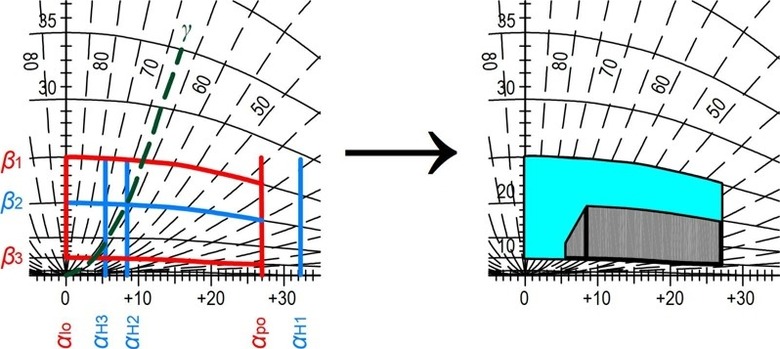
Obrázek 15: Princip práce s Wladramovým diagramem – zakreslení osvětlovacího otvoru a stínícího objektu pro následné určení plochy, kterou v diagramu zaujímá obloha (azurově) a stínící objekt (šedě)
4.2 Princip práce s W-diagramem pro osvětlení svislé roviny v exteriéru
Je-li třeba pro osvětlení svislé roviny v exteriéru využít Waldramův diagram, musí se sestrojit tak, aby správně zohledňoval gradaci oblohy při osvětlení svislé roviny. Waldramův diagram znázorněný na obr. 12 lze použít pouze pro
- svislou srovnávací rovinu v exteriéru,
- tmavý terén a zataženou oblohu v zimě (diagram již zohledňuje gradace jasu oblohy 1:3),
- činitel jasu průčelí stínících objektů i terénu s hodnotou kγ = 0,1.
Křivky znázorněné plnou čarou slouží k zakreslení vodorovných částí stínícího objektu, které jsou rovnoběžné s rovinou osvětlovacího otvoru. Křivky znázorněné přerušovanou čarou slouží k zakreslení vodorovných částí stínícího objektu, které jsou kolmé na rovinu osvětlovacího otvoru. Svislé hrany se zakreslí jako kolmice na hlavní osu diagramu. Při tomto způsobu použití se činitel denní osvětlenosti svislé roviny v exteriéru Dw (%) stanoví
kde
Dws (%) je oblohová složka tohoto činitele (světlo rozptýlené v atmosféře, které do kontrolního bodu dopadá z oblohy),
(53)
Dwe (%) je složka činitele denní osvětlenosti svislé roviny v exteriéru odražená od stínící překážky a od terénu.
(54)
Význam a určení veličin ve výše uvedených vzorcích je shrnuto v tabulce 4. Hodnoty obou složek se opět uvádějí v procentech s přesností na dvě desetinná místa.
| Označení a název dílčí veličiny | Výpočet dílčí veličiny | |
|---|---|---|
| Dws,max (%) | oblohová složka činitele denní osvětlenosti svislé roviny v exteriéru při volném horizontu (nic nestíní) | Dws,max = 
Dws,max ≈ 39,62 % |
| Pe (mm2) | plocha, kterou v diagramu zaujímá stínící překážka | vymezení plochy pomocí Waldramova diagramu pro osvětlení svislé roviny v exteriéru |
| P0 (mm2) | plocha čtverce (obdélníku) v levém horním rohu diagramu | |
Princip práce s upraveným Waldramovým diagramem pro osvětlení svislé roviny v exteriéru je obdobný jako v kapitole 4.1. Příklad výstupu je uveden na obrázku dále v textu.
5. Výpočty na PC
V současné době v praxi převládají výpočty činitele denní osvětlenosti na počítačích. S jedinou výjimkou [17] příslušné softwary využívají promyšlenější, přesnější, a hlavně rychlejší algoritmy založené rovněž na fotometrii plošného zdroje světla. Zvláštní kapitolu tvoří vnitřní odražená složka činitele denní osvětlenosti Di (%), jejíž výpočet na PC vykazuje vyšší přesnost než dříve používané odhady.
![Obrázek 16: Upravený výstup softwaru SVĚTLO+ názorně hodnotí stínění budovami (podle [18])](/docu/clanky/0263/026344o32.jpg)
Obrázek 16: Upravený výstup softwaru SVĚTLO+ názorně hodnotí stínění budovami (podle [18])
Graficko-početní metody se dnes používají například při výuce studentů na stavebních školách [8] a mohou sloužit při kontrole výpočtů pořízených počítačem, zejména v případě řešení sporů o stínění. Před automatickými výpočty mají grafické metody výhodu v jasném, průhledném a srozumitelném postupu výpočtu a v názorném výsledku. Například český software SVĚTLO+ sice počítá činitel Dw (%) vysoce sofistikovanou relativně rychlou a přesnou metodou, ale ve svém výstupu vykreslí i dnes už zdánlivě nepotřebný Waldramův diagram. Na obrázku 16 je na výstupu z PC v diagramu červeně vyšrafován obrys novostavby. Obrázek tak názorně dokládá malý podíl novostavby na zastínění bytu stěžovatelů na zastínění. Názorně je prokázáno, že dominantně stíní jiné objekty.
6. Závěr
Článek se zabývá vybranými graficko-početními metodami (Daniljuk, Waldram). Je popsán princip konstrukce používaných diagramů i matematické zdůvodnění pro čistě početní metodu. I přes masivní používání výpočetní techniky v posledních letech, mají stále tyto tradiční graficko-početní metody své přednosti v názornosti postupu výpočtu a v prezentaci výsledků. Své místo najdou i při sporech, kdy jimi lze jednoznačněji prokázat správnost daného řešení. Odborné softwary totiž mnohdy mají princip výpočtu skrytý a jejich výstupy často neobsahují všechny údaje vstupující do výpočtu a navíc nejsou zcela odolné proti případným dodatečným úpravám.
6. Literatura
- ČSN 73 0511 Denní osvětlení průmyslových budov (1956).
- CIE 215:2014 CIE Standard General Sky Guide (2014).
- LAMBERT, J. H. Photometria sive de mensura et gradibus luminis, colorum et umbrae. Augsburg: Detlefsen, 1760.
- ČSN 36 0035 Denní osvětlení budov (1968).
- MOON, P. – SPENCER, D. E. Illumination from a non – uniform sky. Illuminating Engineering, 1942, (37)10, 707-726.
- ČSN EN 17037 Denní osvětlení budov (2019).
- DANILJUK, A. M. Diagramy dla raščota osveščenosti ot svetoprojomov proizvolnogo očertanija i naklona. Svetlotechnika, 1935, (6)6, 7-9.
- VYCHYTIL, J.: Stavební světelná technika – cvičení. ČVUT Praha, 2015, 156 s., ISBN 978-80-01-05858-9.
- KAŇKA, J. Inovovaný způsob použití Daniljukovy metody. Světlo, 2011, (14)4, 44–46.
- VYCHYTIL, J. – KAŇKA, J.: Stavební světelná technika – přednášky. ČVUT Praha, 176 s., 2016, ISBN 978-80-01-06060-5.
- WALDRAM, P. J. A measuring diagram for daylight illumination. London: B. T. Batsford Ltd., 1950, 19 s.
- HALAHYJA, M. a kol: Stavebná tepelná technika, akustika a osvetlenie, Alfa Bratislava 1985.
- KAŇKA, J. Použití Waldramova diagramu při stanovení činitele denní osvětlenosti. Stavební obzor, 1993, (2)6, 157–159.
- ČSN 73 0580 Denní osvětlení budov – základní požadavky (2007)
- KAŇKA, J. Stanovení činitele denní osvětlenosti svislé roviny okna Waldramovým diagramem upraveným v ČVUT Praha. Světlo, 2002, (5)1, 18–19.
- KAŇKA, J: Vybrané stati ze stavební světelné techniky, ČVUT Praha 2014
- KAŇKA, J. – PELECH, M. Program pro výpočet činitele denní osvětlenosti WAL 1.1. Projektování a výstavba, 1995, 1–2, 39–43.
- Archiv firmy Osvětlení Oslunění Akustika – Ing. Jan Kaňka (IČ: 13158686)
The article deals with the description of selected graphic-numerical methods used to determine the amount of daylight. The principle of derivation of these methods is explained and the principle of working with the relevant diagrams is described. Nowadays, we rarely see the use of diagrams in practice, but some professional software uses them either directly or at least in their graphical outputs.
