Deklinace slunce v průběhu desetiletí
Vztah uvedený v ČSN 730581 pro výpočet sluneční deklinace se bude v průběhu let stále více rozcházet se skutečností. V současné době je jeho nepřesnost vztažená ke čtyřletému průměru hodnot deklinace pro poledne 1. března pouze necelých 8 úhlových minut. Důležité poznatky k posouzení oslunění budov zazněly na konferenci Aktuální problémy osvětlení a oslunění budov.
Úvod
Deklinace δ (°) je úhel, který svírá spojnice středu Slunce se středem Země (čili směr slunečních paprsků) s rovinou zemského rovníku. Při pohybu Země okolo Slunce během roku hodnota deklinace kolísá přibližně od −23,45° do +23,45°. Nejvyšší hodnotu má v době letního slunovratu, zpravidla 21. června, nejnižší v době slunovratu zimního, zpravidla 22. prosince a v době rovnodennosti 21. března a zpravidla 22. září je její hodnota nulová. Deklinace je důležitým parametrem při výpočtu azimutu a výšky slunce a její hodnota je tedy nezbytná pro výpočty sloužící k posouzení oslunění budov podle [2].
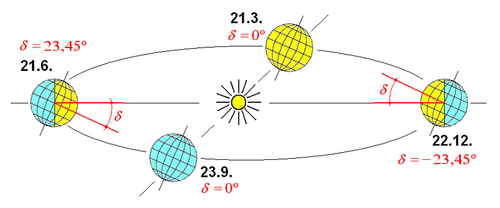
Obr. 1 Dráha Země okolo Slunce a změna deklinace během roku
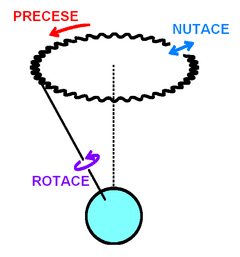
Kdyby osa zemské rotace zachovávala v prostoru stále stejný směr, deklinace by se každý rok opakovala ve stejných hodnotách. Bohužel tomu tak není. Osa zemské rotace totiž koná krouživý pohyb, při kterém opisuje plášť kužele (viz obr. 2). Tento pohyb se nazývá precese. Nebeský severní pól se v současné době nachází asi 1° od hvězdy Polárka v souhvězdí Malého medvěda. V důsledku precese tento pól mění svoji polohu. Například kolem roku 10 000 bude osa rotace Země směřovat do blízkosti hvězdy Deneb v souhvězdí Labutě. Při krouživém pohybu se nebeský pól vrátí na stejné místo přibližně za 25 800 let. Tato perioda se nazývá Platónský rok. Precese nemá významný vliv na přesnost výpočtů polohy slunce na obloze, protože se jedná o pohyb relativně pomalý. Významnější roli hraje nutace, která se projevuje malými výkyvy zemské osy při precesním pohybu, takže povrch kužele, který opisuje zemská osa je jakoby vlnitý. Nutace je pohyb méně pravidelný, protože se skládá z více dílčích periodických pohybů. Nejvýznamnější perioda nutace je 18,6 roku.
Příčinou precese je skutečnost, že naše planeta nemá tvar koule, ale přibližně rotačního elipsoidu, na který působí gravitační síly Slunce a Měsíce. Ty se snaží osu rotace Země vychýlit tak, aby se rovina zemského rovníku ztotožnila s rovinou oběhu Měsíce okolo Země resp. s rovinou oběhu Země okolo Slunce. Protože tyto roviny nejsou totožné, dochází při gravitačním působení k jakémusi „přetahování“, jehož výsledkem je precesní pohyb zemské osy. Nutace je pak způsobena gravitačními silami ostatních planet sluneční soustavy, které se k výše uvedenému jevu přidávají. Kromě gravitačních vlivů se podílí na vychýlení zemské osy i slapové síly (příliv a odliv), vliv mořských proudů a další vlivy například velká zemětřesení. Následkem nutace a precese není průběh hodnot deklinace v každém roce stejný. Hodnoty deklinace s přesností na úhlové vteřiny pro 0:00 hodin každého dne lze nalézt ve hvězdářských ročenkách.
Hodnoty deklinace podle ročenek
Hvězdářské ročenky byly v Československé republice vydávány od roku 1921 a jsou vydávány i v České republice nepřetržitě až do současnosti. Pouze ve válečných letech 1942 až 1945 ročenka nebyla vydána. Nákupem hvězdářských ročenek v antikvariátech a studiem v knihovnách byly získány hodnoty deklinace δ1 (°) resp. δ2 (°) v 0:00 hodin dne prvního resp. druhého března v souvislé řadě od roku 1928 až do současnosti. Hodnoty z neexistujících ročenek z let 1942 až 1945 byly doplněny podle analogie. K šetření byl vybrán den 1. března, protože právě k tomuto datu se vztahují požadavky ČSN 734301. Hodnota deklinace se nemění skokem ze dne na den, ale plynule. Protože k oslunění budov může docházet během celého dne, byla hodnota deklinace stanovena pro 12:00 hodin dne 1. března jako průměr z obou hodnot.
Takto získané hodnoty δ (°) byly vyneseny do diagramu (viz obr. 3). Čtyřleté cykly, které diagram vykazuje, jsou pravděpodobně způsobeny přestupnými roky. Z diagramu je patrné, že v průběhu desetiletí hodnoty deklinace stále rostou tj. přibližují se k nule. Červeně je v diagramu vyznačena hodnota deklinace δ = −7,6 stanovená pro den prvního března podle vztahu (2).
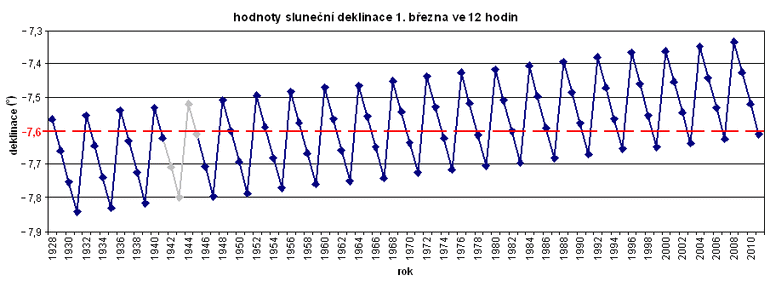
Obr. 3 Hodnoty sluneční deklinace 1. 3. ve 12 hodin
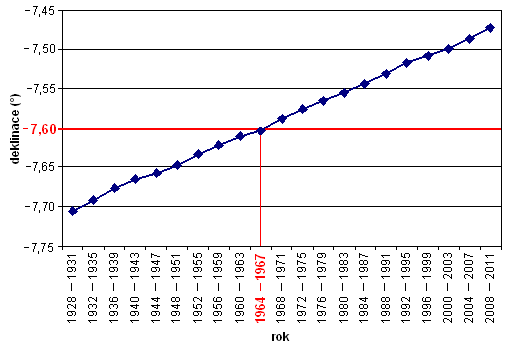
Obr. 4 Hodnoty čtyřletých průměrů deklinace dne 1. 3. v létech 1928 až 2011
Na obrázku 4 jsou formou diagramu vyneseny hodnoty čtyřletých průměrů deklinace Slunce mezi léty 1928 až 2011. Je zřejmé, že za 84 let sledování vzrostly průměrné hodnoty deklinace o cca 25 úhlových minut. Tento nárůst bude v dalších letech zřejmě pokračovat. Hodnota δ = −7,6° vypočtená pro den 1. 3. podle vztahu (2) je v diagramu opět vyznačena červenou čarou. Vztah (2) tedy platil nejpřesněji v šedesátých létech minulého století. V současné době se čtyřletý průměr deklinace Slunce liší od této hodnoty o 7 minut a 50 vteřin úhlové míry.
Stanovení deklinace pro technické účely
Při technickém hodnocení proslunění bytů podle [2] se posuzuje doba oslunění dne 1. března. Kdyby se při tomto hodnocení oslunění vycházelo z přesných hodnot deklinace, zdánlivá dráha slunce po obloze v tento den by byla v každém roce poněkud jiná. V extrémním případě by se mohlo stát, že v jistém roce by proslunění bytu vyhovělo požadavkům normy a v jiném roce by nevyhovělo. Taková praxe by byla jistě nepřípustná, a proto je v [1] uveden vztah (2) pro výpočet průměrné hodnoty deklinace. S hodnotou deklinace, která se stanoví podle tohoto vztahu, se počítá vždy bez ohledu na skutečnou hodnotu, která je pro den 1. března ve hvězdářské ročence v daném roce uvedena. Technická praxe zde oprávněně dává přednost jednotnosti výpočtu před jeho přesností. Vztah (2) byl do normy převzat z literatury [4].
kde D je číslo dne v měsíci a M číslo měsíce v roce. Pro 1. března tak vychází
Závěr
Vztah (2) uvedený v ČSN 730581 pro výpočet sluneční deklinace se bude v průběhu let stále více rozcházet se skutečností. V současné době je jeho nepřesnost vztažená ke čtyřletému průměru hodnot deklinace pro poledne 1. března pouze necelých 8 úhlových minut. Největší rozdíl mezi hodnotou stanovenou podle (2) a skutečnou hodnotou podle hvězdářské ročenky nepřesáhne v současné době 18 úhlových minut. Hodnotu δ = −7,6036° stanovenou pro den prvního března podle (2) je možno bez obav dále používat při posuzování proslunění budov. Tato hodnota je neměnná a je nezbytným konsensem v situaci, kdy technické výpočty nemohou akceptovat celou složitost mechaniky planety Země.
LITERATURA
- [1] ČSN 730581 Oslunění budov a venkovních prostor – metoda stanovení hodnot (2009)
- [2] ČSN 734301 Obytné budovy (2004)
- [3] ČSN 734301 Obytné budovy Změna Z1(2005)
- [4] Puškáš, J: Slnko v urbanizme a architektúre, Alfa Bratislava 1992
- [5] Soubor hvězdářských ročenek z let 1928 až 2011, Astronomický ústav AV ČR, Ondřejov
The formula specified in CSN 730581 for calculating the solar declination will over the years increasingly diverge with reality. At present, its relative inaccuracy of the four-year average of the declination for noon first March is just under 8 minutes of arc. Important information for assess the insolation of buildings raised at the conference Current Issues of lighting and solar access of buildings.