Rozšíření Sharpovy metody pro výpočet vzduchové neprůzvučnosti stavebních konstrukcí
Semi-empirické metody pro výpočet neprůzvučnosti slouží pro dosažení finančních úspor ve fázi návrhu stavby. Článek prezentuje sadu rovnic, které rozšiřují Sharpovu metodu, a porovnává různé výpočetní postupy s měřením. Publikace se zabývá jak jednoduchými, tak dvojitými stavebními konstrukcemi.
Abstrakt
Vzduchová neprůzvučnost stavebních konstrukcí je předmětem stálého zájmu navrhujících projektantů a architektů. Přestože je vážená stavební neprůzvučnost v závěrečné fázi ověřována měřením v již realizovaných stavbách, mají semi-empirické metody potenciál nezanedbatelných finančních úspor ve fázi návrhu stavby. Článek prezentuje sadu rovnic vhodných pro výpočet vzduchové neprůzvučnosti jednoduchých a dvojitých stavebních konstrukcí, která rozšiřuje Sharpovu metodu. Rovnice jsou odvozeny matematickými postupy, ale cílem tohoto článku je dodat čtenáři připravený výpočetní nástroj, a proto je samotné odvození uvedeno v jiných publikacích. Sada rovnic je porovnána s laboratorními měřeními a jinými metodami jak pro jednoduché (EN 12354-1, Davyho a Wattersova metoda), tak pro dvojité konstrukce (Davyho a Wattersova metoda).
1. Úvod
Vzduchovou neprůzvučnost stavebních konstrukcí je možné vypočíst řadou metod, které se liší dle toho, jak byly odvozeny a dle komplexnosti výpočtu. V inženýrské praxi jsou populární semi-empirické metody, které jsou snadno pochopitelné a rychle použitelné.
Mezi další možnosti modelování šíření zvuku stavebními konstrukcemi patří numerické metody jako metody konečných nebo hraničních prvků. Velmi detailně a s důrazem na lehké konstrukce je tato problematika rozpracována v disertační práci [1]. Tyto výpočetní postupy jsou komplexní a jsou založeny na řešení parciálních diferenciálních rovnic.
Zlatou střední cestou je statistická analýza energie, která vychází z rozdělení konstrukce na subsystémy přenášející různé typy vln (ohybové, podélné a smykové). Předmětem zájmu této metody je energie a jejím cílem je vyjádřit, jaká část energie byla mezi subsystémy přenesena, uchována nebo ztracena disipací. Velmi dobrou implementací je SEAlab naprogramovaná v jazyce Matlab, jejíž vývoj byl popsán v publikaci [2].
Cílem tohoto článku je však popsat rovnice, které jsou snadno použitelné pro rychlý a v rámci možností i přesný výpočet neprůzvučnosti konstrukce. Jejich výhodou je právě vhodnost pro praktické inženýrské výpočty snadno aplikovatelné pro návrh konstrukcí.
2. Jednoduché konstrukce
![Obr. 1: Neprůzvučnost jednoduché isotropické stěny v závislosti na frekvenci (volně dle [3])](/docu/clanky/0144/014441o1.jpg)
Obr. 1: Neprůzvučnost jednoduché isotropické stěny v závislosti na frekvenci (volně dle [3])
Neprůzvučnost jednoduché stavební konstrukce je schematicky popsána na Obr. 1. Průběh neprůzvučnosti je rozdělen do pěti výpočtových pásem. Nárůst neprůzvučnosti ve II. a V. frekvenčním pásmu je 6 dB na oktávu, zatímco ve IV. frekvenčním pásmu roste neprůzvučnost o 9 dB na oktávu.
2.1. Oblast fundamentální rezonance (I.)
V okolí fundamentální rezonance f0 se nachází výrazný pokles neprůzvučnosti. Fundamentální rezonance stavební konstrukce by proto měla být navržena pod zvukově izolačním pásmem (tj. pod 100 Hz) nebo v ideálním případě pod rozšířeným zvukově izolačním pásmem (tj. pod 50 Hz). Rezonanční frekvence různých řádů mohou být vypočteny jako [3]:
(1)
kde fi,n [Hz] je rezonanční frekvence různých řádů (fundamentální frekvence je rezonancí prvního řádu ve směru obou os), B [kg m2 s−2] je ohybová tuhost na jednotku šířky, m [kg/m2] je plošná hmotnost, i [–] a n [–] jsou řády rezonance, lx [m] a ly [m] jsou rozměry konstrukce.
2.2. Oblast platnosti zákona hmotnosti (II.)
Zákon hmotnosti byl odvozen v [4] a přehledný postup odvození lze nalézt i v [5]. Neprůzvučnost jednoduché stěny v oblasti platnosti zákona hmotnosti je možné vypočíst [3]:
(2)
kde f [Hz] je frekvence, ρ0 [kg/m3] je hustota vzduchu a c0 [m/s] je rychlost zvuku ve vzduchu.
Neprůzvučnost v oblasti zákona hmotnosti je také možné vypočíst (dle odvození v [6]):
(3)
kde fcr [Hz] je kritická frekvence [3]:
(4)
kde t [m] je tloušťka stěny a cL [m/s] je rychlost ohybových vln. Kritickou frekvenci je také dle ČSN EN 12354-1 [7], která v tomto ohledu čerpá z [8] a [9], možné nahradit efektivní kritickou frekvencí fc,eff [Hz]. Efektivní kritická frekvence slouží k zahrnutí dalších typů vln důležitých pro silné stěny pro vyšší frekvence, než kritická frekvence vypočtená dle Rov. 4.
Jestliže f < fp, potom [7]:
(5)
Jestliže f ≥ fp, potom [7]:
(6)
kde frekvence fp se rovná: cL / (5,5 t).
Limitní úhel dopadu zvukové vlny θl [°] můžeme fixně dle Sharpova přístupu nastavit v rozmezí 78° a 85° [10]. Nebo je možné limitní úhel dopadu vypočíst dle [6] a [11]:
(7)
kde A [m2] je plocha stavební konstrukce.
2.3. Pokles neprůzvučnosti pod kritickou frekvencí (III.)
Neprůzvučnost v oblasti poklesu neprůzvučnosti pod kritickou frekvencí můžeme vyjádřit pomocí jednoduché lineární interpolace [6]:
(8)
kde koeficient a se vypočte [6]:
(9)
kde ηTOT [–] je celkový ztrátový činitel, který může být vypočten z vnitřního ztrátového činitele rovnicemi uvedenými v [7]. Koeficient b se vypočte [6]:
(10)
Frekvence fmax [Hz], která rozděluje oblasti II. a III., je popsána rovnicí [6]:
(11)
2.4. Nárůst neprůzvučnosti nad kritickou frekvencí (IV.)
Neprůzvučnost nad kritickou frekvencí je možné vyjádřit vztahem [4] [6] [12]:
(12)
2.5. Oblast platnosti zákona hmotnosti (V.)
Publikace [3] doporučuje, aby neprůzvučnost nad kritickou frekvencí vypočtená dle Rov. 12 nepřesáhla neprůzvučnost dle zákona hmotnosti. V tomto případě však formulace zákona hmotnosti (Rov. 3) neobsahuje člen pro kritickou frekvenci [6]:
(13)
Neprůzvučnost dle Rov. 13 je platná pro frekvenci vyšší než limitní frekvence fl [6]:
(14)
2.6. Komparativní případová studie: jednoduchá konstrukce
![Obr. 2: Neprůzvučnost stěny z betonových bloků tloušťky 90 mm v závislosti na frekvenci (experiment z [15])](/docu/clanky/0144/014441o17.png)
Obr. 2: Neprůzvučnost stěny z betonových bloků tloušťky 90 mm v závislosti na frekvenci (experiment z [15])
Je zde předvedeno srovnání výpočtu neprůzvučnosti dle metody navržené v publikaci [6], ČSN EN 12354-1 [7], Wattersovy metody [13], Davyho metody [14] (recenzovaná v [3]) a výsledků experimentu [15]. Neprůzvučnost stěny z betonových bloků je zobrazena na Obr. 2.
Modelovaná stěna z betonových bloků má tyto materiálové vlastnosti:
- t = 90 mm (tloušťka),
- ρ = 2170 kg/m3 (objemová hmotnost),
- cL = 3500 m/s (rychlost šíření vln v materiálu),
- ηint = 0,006 (vnitřní ztrátový činitel).
3. Dvojité konstrukce
![Obr. 3: Diagram výpočtu neprůzvučnosti dvojité isotropické stěny v závislosti na frekvenci (dle [3]). Průběh pro dřevěné sloupky je vyznačen plnou čarou, průběh pro ocelové sloupky je vyznačen čárkovaně.](/docu/clanky/0144/014441o19.jpg)
Obr. 3: Diagram výpočtu neprůzvučnosti dvojité isotropické stěny v závislosti na frekvenci (dle [3]). Průběh pro dřevěné sloupky je vyznačen plnou čarou, průběh pro ocelové sloupky je vyznačen čárkovaně.
Diagram výpočtu neprůzvučnosti dvojité stavební konstrukce je zobrazen na Obr. 3. Predikce neprůzvučnosti dvojitých stavebních prvků je komplikována skutečností, že tyto prvky mohou být propojeny akustickými mosty, tj. např. dřevěnými nebo ocelovými sloupky. Článek nepopisuje situaci, kdy se spojení modelují jako bodová, např. dřevěný rošt.
Dřevěné sloupky je možné považovat za tuhé, liniové spojení dílčích konstrukcí. Ocelové sloupky je naopak možné považovat za pružinové spojení a přenos zvuku skrz ocelové sloupky je zanedbatelný ve srovnání s přenosem zvuku vzduchovou dutinou. Je doporučeno pro přenos zvuku ocelovými sloupky používat empirickou korekci 0,04 ve srovnání s dřevěnými sloupky [11]. V obou případech je uvažováno s tím, že vzduchová dutina mezi dílčími konstrukcemi je zatlumená širokopásmovým pohlcovačem, který zamezuje vzniku stojatého vlnění.
3.1. Fundamentální rezonance dvojité konstrukce (I.)
Fundamentální rezonance f0 [Hz] dvojité konstrukce se vypočte [16]:
(15)
kde m1 [kg/m2] a m2 [kg/m2] jsou plošné hmotnosti dílčích konstrukcí a d [m] je tloušťka vzduchové mezery. Korekci 1,8 zavedl Sharp v [17], nicméně Davy [11] tuto korekci nepoužívá.
Neprůzvučnost dvojité konstrukce v této oblasti nezávisí na způsobu spojení dílčích konstrukcí a vypočte se [10]:
(16)
3.2. Oblast s mezní frekvencí (II.)
Druhá frekvenční oblast pro dvojité konstrukce je ohraničena mezní frekvencí fB [Hz] („bridging frequency“), která vymezuje oblast, ve které má vliv druh spojení dílčích konstrukcí. Mezní frekvence fB se pro liniová spojení vypočte (odvozeno na základě rovnic v [3] analytickou geometrií):
(17)
kde l [m] je vzdálenost mezi liniovými podporami (tj. dřevěnými sloupky) a fcr,1 a fcr,2 jsou kritické frekvence dílčích panelů, přičemž platí, že fcr,2 ≥ fcr,1.
Neprůzvučnost RII se rovná [10]:
(18)
kde R1 [m] a R2 [m] jsou neprůzvučnosti dílčích konstrukcí a k [m−1] je vlnové číslo.
3.3. Ocelové sloupky (III., IV., V. a VI. oblast)
Přenos zvuku sloupky na bázi oceli se v tomto případě považuje za zanedbatelný a zvuk se proto šíří pouze vzduchovou dutinou, u které se předpokládá vyplnění širokopásmovým pohlcujícím materiálem. Oblast III je pro ocelové sloupky pouze rozšířením oblasti II a neprůzvučnost RIII se proto vypočte [10]:
(19)
Oblast III je ohraničena limitní frekvencí fl [Hz], pro kterou platí [3]:
(20)
Neprůzvučnost dvojité konstrukce s ocelovými sloupky v oblastech IV, V a VI se vypočte [10]:
(21)
3.4. Dřevěné sloupky (III., IV., V. a VI. oblast)
Na Obr. 3 je naznačeno, že neprůzvučnost dvojité konstrukce by neměla klesnout pod teoretické minimum definované čerchovanou čárou (neprůzvučnost RI dle Rov. 16).
Neprůzvučnost ve III. a IV. oblasti se vypočte [3]:
(22)
Oblast IV je od oblasti V oddělena 1/2 kritické frekvence fcr,2 dílčí konstrukce, pro kterou platí, že fcr,2 ≥ fcr,1. Neprůzvučnost v oblasti V se vypočte (odvozeno na základě rovnic v [3] analytickou geometrií):
(23)
Pokud fcr,2 = fcr,1, pak se koeficient a vypočte:
(24)
Pokud fcr,2 > fcr,1, pak se koeficient a vypočte:
(25)
kde ηTOT,2 a ηTOT,1 jsou celkové ztrátové činitele a patří k dílčím konstrukcím se shodným indexováním jako fcr,2 a fcr,1.
Koeficient b se vypočte:
(26)
Pro neprůzvučnost v poslední oblasti VI platí, že pokud fcr,2 = fcr,1, pak (odvozeno na základě rovnic v [3] analytickou geometrií):
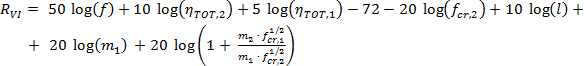(27)
Pokud fcr,2 > fcr,1, pak neprůzvučnost v poslední oblasti VI lze popsat vztahem (odvozeno na základě rovnic v [3] analytickou geometrií):
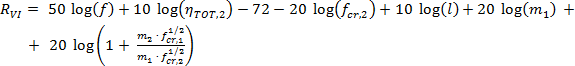(28)
3.5. Komparativní případová studie: dvojitá konstrukce s dřevěnými sloupky
Obr. 4: Geometrie dvojité konstrukce s dřevěnými sloupky
![Obr. 5: Neprůzvučnost dvojité stěny ze sádrokartonových desek v závislosti na frekvenci (experiment z [18])](/docu/clanky/0144/014441o37.png)
Obr. 5: Neprůzvučnost dvojité stěny ze sádrokartonových desek v závislosti na frekvenci (experiment z [18])
Byla vypočtena neprůzvučnost dvojité stěny ze dvou sádrokartonových desek spojené dřevěnými sloupky. Neprůzvučnost je vypočtena dle rozšířené Sharpovy metody (viz Rov. 22 až 28), Wattersovy metody [13], Davyho metody [11] (recenzovaná v [3]) a výsledků experimentu [18]. Neprůzvučnost dvojité stěny v závislosti na frekvenci je na Obr. 5.
Geometrie konstrukce je zobrazena na Obr. 4. Vlastnosti sádrokartonové desky jsou:
- t = 13 mm (tloušťka),
- m = 10,1 kg/m2 (plošná hmotnost),
- E = 2 ‧ 109 m/s (Youngův modul pružnosti),
- ηTOT = 0,1 (celkový ztrátový činitel).
4. Závěr
Rozšířená Sharpova metoda byla prezentována v dostatečné podrobnosti, aby čtenář mohl uvedené rovnice použít k vlastním výpočtům. Výpočty je v současné době možné provádět v tabulkovém procesoru nebo v Matlabu. Nebylo popsáno samotné odvození rovnic, protože se předpokládá především zájem o jejich praktické uplatnění. V případě zájmu o studium teoretického zázemí jsou čtenáři odkázáni na seznam literatury.
Porovnání metod s měřením, které je zobrazeno na Obr. 2 pro jednoduché konstrukce a na Obr. 5 pro dvojité konstrukce, ukazuje, že přestože se mezi užitými metodami vyskytují rozdíly, je celková shoda mezi nimi uspokojivá. Je proto možné uvedené rovnice doporučit pro předběžný návrh stavebních konstrukcí.
5. Poděkování
Tato práce vznikla za finanční podpory MŠMT v rámci programu NPU I č. LO1605 – Univerzitní centrum energeticky efektivních budov – Fáze udržitelnosti.
6. Literatura
- POBLET-PUIG, J. Numerical modelling of sound transmission in lightweight structures. Disertační práce. Universitat Politecnica de Catalunya Programa de Doctorat d'Enginyeria Civil. Laboratori de Calcul Numeric. Barcelona. 2008.
- JOHANSSON, D., COMNELL, P. Statistical Energy Analysis software: Development and implementation of an open source code in Matlab/Octave. Diplomová práce. Department of Civil and Environmental Engineering. Chalmers University of Technology. Göteborg, Sweden. 2010.
- BIES, D. A., HANSEN, C. H. Engineering Noise Control: Theory and Practice, Third Edition. CRC Press, 2003. ISBN 978-0-41-526714-4.
- CREMER, L. Theorie der Schälldammung dünner Wände bei schrägem Einfall. Akust. Zeitschrift 7, pp. 81–104, 1942.
- LONDON, A. Transmission of Reverberant Sound Through Single Walls. Part of the Journal of Research of the National Bureau of Standards, vol. 42, 1949.
- ŠLECHTA, J. Transmission Loss of Single Walls with Respect to the Limiting Angle of the Incident Sound Wave. Akustika. 2016, vol. 25, pp. 10–21. ISSN 1801-9064.
- ČSN EN 12354-1: Stavební akustika. Výpočet akustických vlastností budov z vlastností stavebních prvků. Část 1: Vzduchová neprůzvučnost mezi místnostmi. 2001.
- LJUNGGREN, S. Airborne sound insulation of thick walls. The Journal of the Acoustical Society of America 89, pp. 2338–2345, 1991.
- GERRETSEN, E. Calculation of airborne and impact sound insulation between dwellings. Applied Acoustics 19, pp. 245–264, 1986.
- SHARP, B. H. Prediction Methods for the Sound Transmission of Building Elements. Noise Control Engineering 11, pp. 55–63, 1978.
- DAVY, J. Predicting the sound insulation of walls. Building Acoustics, vol. 16, no. 1, pp. 1–20, 2009. ISSN 1351-010X.
- JACOBSEN, F. et al. Fundamentals of Acoustics and Noise Control. Department of Electrical Engineering, Technical University of Denmark, Note no 31200, 2011.
- KAŇKA, J. Stavební fyzika 1: Akustika budov. Praha, ČVUT v Praze, 2007. ISBN 978-80-01-03664-8.
- DAVY, J. L. A Model for Predicting the Sound Transmission Loss of Walls. The Australian Vibration and Noise Conference 1990. The Institution of Engineers. Canberra, pp. 23–27, 1990.
- WARNOCK, A. C. C., MONK, D. W. Sound Transmission Loss of Masonry Walls: Tests on 90, 140, 190, 240 and 290 mm Concrete Block Walls with Various Surface Finishes. National Research Council Canada, Division of Building Research, Building Research Note No. 217, 1984. ISSN 0701-5232.
- FAHY, F. J. Sound and Structural Vibration: Radiation, Transmission and Response. London, Academic Press, 1985. ISBN 0-12-247670-0.
- SHARP, B. H. A Study of Techniques to Increase the Sound Installation of Building Elements. Wylie Laboratories, Report WR 73-S, Washington, DC, under contract H-1095, 1973.
- HALLIWELL, R. E., NIGHTINGALE, T. R. T., WARNOCK, A. C. C., BIRTA, J. A. Gypsum Board Walls: Transmission Loss Data. Internal Report IRC-IR-761. Institute for Research in Construction, National Research Council of Canada. Ottawa, 1988.
The airborne sound insulation of building structures is a subject of permanent interest of designing engineers and architects. Although the weighted apparent sound reduction index is in the final phase verified by measurements in already established buildings, semi-empirical methods have a potential of non-negligible financial savings in the building design phase. The paper presents a set of equations convenient for the calculation of the airborne sound insulation of single and double building structures which extends the Sharp’s method. The equations are derived by mathematical procedures but the purpose of this paper is to supply the reader with a prepared computational tool and that’s why the derivation is listed in different publications. The set of equations is compared with laboratory measurements and other methods both for single (EN 12354-1, Davy’s and Watters’ method) and double structures (Davy’s and Watters’ method).
