Doba dozvuku staveb pro sport a tělovýchovu
Článek se zabývá problematikou výpočtového odhadu doby dozvuku sportovních staveb ve fázi projektové přípravy. Na souboru devíti vybraných staveb je provedeno porovnání výsledků výpočtů s hodnotami změřenými in-situ na dokončených stavbách. Pro výpočty byly zvoleny různé predikční metody a počítačové simulace.
Úvod
Sportovní stavby jsou z hlediska prostorové akustiky charakteristické velkým obestavěným objemem a často také nerovnoměrně rozloženou pohltivostí zvuku. Strop bývá jedním z mála vhodných vnitřních povrchů, na které lze umístit zvukově pohltivé obklady. Tato skutečnost vede k problémům s odhadem doby dozvuku ve fázi návrhu, neboť standardní výpočtové postupy nebývají dostatečně přesné. Možným důvodem může být nedostatečná difuznost zvukového pole prostorů s nerovnoměrně rozloženou pohltivostí i nemožnost zahrnout do výpočtového modelu všechny vlivy, které výslednou dobu dozvuku ovlivňují.
Tyto problémy iniciovaly vznik projektu, který byl realizován na Stavební fakultě ČVUT v Praze v rámci studentské grantové soutěže pro rok 2012. Projekt zahrnoval měření doby dozvuku vybraných sportovních staveb s následnými výpočty doby dozvuku standardními i pokročilými metodami a tvorbou 3D modelů v programu ODEON 10.1. Výsledky výpočtů i měření byly vzájemně porovnány a jsou popsány v tomto článku.
Mohlo by vás také zajímat:Deska CETRIS® pro akustické obklady
Při navrhování, projektování či realizaci stavebních konstrukcí se stále zapomíná na parametry prostorové akustiky. Ve srovnání s jinými akustickými obkladovými materiály je při použití cementotřískových desek CETRIS AKUSTIC nebo CETRIS AKUSTIC FINISH zajištěna navíc vysoká odolnost proti mechanickému proražení (např. míčem) a odolnost vůči vlhkosti – to vše při zachování vysoké třídy reakce na oheň (A2, d0).
Optimální doba dozvuku
![Obr. 1 Optimální doba dozvuku T0 tělocvičny, sportovní haly a plavecké haly v závislosti na objemu podle [3] ČSN 73 0527](/docu/clanky/0094/009450o2.png)
Obr. 1 Optimální doba dozvuku T0 tělocvičny, sportovní haly a plavecké haly v závislosti na objemu podle [3] ČSN 73 0527
Doba dozvuku je základní prostorově akustický parametr uzavřených prostorů. Akustickými úpravami lze dobu dozvuku snížit na optimální úroveň pro daný účel využití prostoru. U staveb pro sport a tělovýchovu se sleduje především snížení hladiny akustického tlaku pozadí (způsobeného hlasovými projevy hráčů nebo diváků, vlastní hrou či technickým zařízením), zlepšení podmínek srozumitelnosti řeči (pro hráče, trenéry a rozhodčí, žáky či pedagogy), event. dosažení přijatelných podmínek pro elektronicky zesilovanou hudbu (například jako doprovod při tanečních vystoupeních). Hodnoty optimální doby dozvuku tělocvičen, sportovních hal a plaveckých hal v závislosti na jejich objemu V [m3] jsou uvedeny na obrázku 1.
Doba dozvuku se sleduje ve čtyřech oktávových pásmech od 250 Hz do 2000 Hz. Přípustná odchylka doby dozvuku od optimální doby dozvuku v tomto kmitočtovém rozsahu je 20 %. U sportovních staveb se neuvažuje obsazení prostoru osobami (tj. hráči ani diváky), hodnotí se neobsazený stav. Normové hodnoty podle ČSN 73 0527 mají obecně doporučující charakter. Výjimku tvoří zařízení a provozovny pro výchovu a vzdělávání, pro která jsou požadavky na dobu dozvuku v souladu s vyhláškou č. 410/2005 Sb. závazné.
Stavební akustika na TZB-info – šíření a pohlcování zvuku, vzduchová a kročejová neprůzvučnost
On-line výpočet neprůzvučnosti
Vybrané prostory
Velikost obestavěných prostorů pro sport a tělovýchovu se odvíjí od základních rozměrů hrací plochy. Největší hrací plochou obvykle bývá basketbalové hřiště, jehož doporučené půdorysné rozměry jsou 15 m × 28 m (ev. minimální rozměry 14 m × 26 m) a světlá výška pod strop nejméně 7 m. Při volném pruhu šířky 2 m okolo hřiště vychází objem tělocvičen cca 4 000 m3 a poměr základních rozměrů 1 : 2,7 : 4,6 (ev. 1 : 2,6 : 4,3). Těmto uzavřeným prostorům je v článku věnována největší pozornost. Mezi devět vybraných staveb však byly zařazeny i multifunkční a bazénové haly s větším objemem (až 21 000 m3).
Dalším výběrovým kritériem, kromě odlišného obestavěného objemu, byl charakter a rozsah akustických úprav. Mezi vybranými prostory jsou tělocvičny a haly s akustickou úpravou pouze stropu, stropu a jedné, popřípadě více bočních stěn, ale i prostory bez akustických úprav. Souhrnný přehled vybraných prostorů je uveden v tabulce 1.
| č. | druh prostoru | obestavěný objem [m3] | základní rozměry [m] | popis akustických úprav |
|---|---|---|---|---|
| 1 | tělocvična (tanec, aerobik) | 372 | 10 × 8 × 4,5 | bez akustických úprav |
| 2 | tělocvična (gymnázium) | 3 500 | 26 × 17 × 7,8 | podhled z desek ze skelných vláken v celé ploše střechy mezi vazníky, dřevěný laťový obklad na příčných stěnách |
| 3 | tělocvična (základní škola) | 3 700 | 29,5 × 15 × 8,2 | pod stropem zavěšena akustická tělesa (baffles), na jedné příčné a jedné podélné stěně akustický obklad z desek z křemičitého písku |
| 4 | tělocvična (střední škola) | 4 050 | 30 × 18 × 7,5 | podhled z kazet ze skelných vláken v celé ploše střechy |
| 5 | tělocvična (základní škola) | 5 450 | 36 × 18 × 8,5 | podhled z kazet ze skelných vláken v celé ploše střechy + obklad z panelů ze skelných vláken na jedné příčné stěně |
| 6 | tělocvična (míčové hry, různé sportovní akce) | 7 100 | 51,5 × 17 × 8 | bez akustických úprav |
| 7 | sportovní hala (200 sedících diváků) | 16 200 | 44,5 × 29,5 × 12,3 | pruhy panelů z minerálních vláken pod stropem + obklad z panelů z minerálních vláken na všech stěnách |
| 8 | sportovní hala (500 sedících diváků) | 17 000 | 45 × 34 × 13 | podhled z panelů ze skelných vláken v celé ploše střechy + pruh z panelů ze skelných vláken na podélné stěně |
| 9 | bazénová hala (aquapark) | 21 400 | 59 × 32,5 × 11 | akustický obklad části střechy z desek z křemičitého písku + dílčí kazetové minerální podhledy na vnitřních plochách |
Měření doby dozvuku
Obr. 2 Měření doby dozvuku v tělocvičně č. 4
Pro vlastní měření doby dozvuku podle [5] ČSN EN ISO 3382-2 byla použita metoda přerušeného šumu. Měřena byla doba dozvuku T20 i T30 v 6 oktávových pásmech od 125 Hz do 4 000 Hz. Výsledná doba dozvuku byla určena jako prostorový průměr z výsledků měření v jednotlivých kombinacích míst zdroje zvuku a mikrofonu, určený pro uzavřený prostor jako celek. Zdrojem zvuku byl všesměrový reproduktor CESVA BP012 se zesilovačem a generátorem šumu AP601.
Výpočet doby dozvuku
Pro výpočet doby dozvuku T [s] vybraných staveb pro sport a tělovýchovu v neobsazeném stavu byly použity čtyři odlišné výpočetní modely. Prvním z nich je model popsaný v [4] ČSN EN 12354-6, který pro výpočet doby dozvuku používá Sabinův vztah:
kde je
- c0
- – rychlost zvuku ve vzduchu [m.s−1],
- V
- – objem prázdného uzavřeného prostoru [m3],
- S
- – celková plocha všech pohltivých povrchů v místnosti [m2],
- αm
- – střední činitel zvukové pohltivosti [–],
- m
- – součinitel útlumu zvuku ve vzduchu v neperech na metr.
Pro prostory s větším množstvím objektů a vybavení se tato skutečnost v modelu zohledňuje nejen zvýšením celkové ekvivalentní pohltivé plochy uzavřeného prostoru, ale též zmenšením obestavěného objemu prostoru. Podle ČSN EN 12354-6 je tento výpočetní model omezen na prostory, které mají všechny tři základní rozměry podobné (tj. žádný rozměr není více než pětinásobkem kteréhokoliv jiného rozměru) a mají rovnoměrně rozloženou pohltivost (činitele zvukové pohltivosti dvou protějších povrchů se neliší více než trojnásobně). Obecně je však třeba poznamenat, že Sabinova teorie je určena především pro prostory s malou pohltivostí (s αm < 0,30). Pro více pohltivé prostory je při výpočtu doby dozvuku teoreticky správnější vycházet z Eyringova vztahu:
Tento výpočetní model doporučuje norma [2] ČSN 73 0525 a byl proto zahrnut i do této práce. Stejně jako v předchozím případě je však také Eyringova teorie určena především pro prostory s rovnoměrně rozloženou pohltivostí. Protože tuto podmínku stavby pro sport a tělovýchovu obvykle nesplňují, v rámci předkládané práce byl použit ještě výpočetní model z přílohy D normy ČSN EN 12354-6, který je určen výhradně pro prostory s nerovnoměrně rozloženou pohltivostí. Doba dozvuku se vypočítá v závislosti na hodnotě přechodového kmitočtu ft mezi nízkými a vysokými kmitočty, který je dán vztahem:
[4] Pro vyšší kmitočty je celkové zvukové pole rozděleno do tří polí, která jsou kolmá k osám x, y a z, a difuzního pole. Pro každé z těchto polí se určí efektivní pohltivost a doba dozvuku. Význam každého z těchto polí je určen počtem vlastních kmitů v těchto polích odvozených z rozměrů místnosti. Pro nižší kmitočty se celkové zvukové pole považuje za pole s omezeným vlivem pohltivost z důvodu nedostatku difuznosti.
Pro nízké kmitočty (f < ft) se doba dozvuku vypočítá ze vztahu:
kde je
- A*xyzd
- – ekvivalentní pohltivá plocha pro celkové zvukové pole [m2].
Pro vyšší kmitočty je doba dozvuku určena následovně:
kde jsou
- Tx, Ty, Tz, Td
- – doby dozvuku pro zvuková pole x, y, z a d [s].
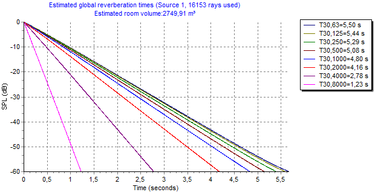
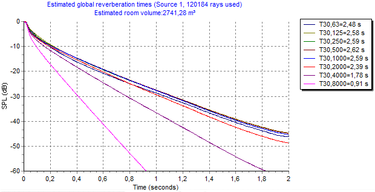
V důsledku nerovnoměrně rozložené pohltivosti není zvukové pole difuzní a křivka poklesu není lineární. Pro prostory se zvukově pohltivým podhledem a neupravenými stěnami dominují osové módy mezi oběma dvojicemi rovnoběžných stěn a tangenciální módy mezi čtyřmi stěnami, zatímco ostatní osové a tangenciální módy včetně šikmých módů jsou utlumeny pohltivým stropem. Doba dozvuku Tz je tedy výrazně delší než doba dozvuku pro zvuková pole x, y a d a určuje výslednou dobu dozvuku T. Tuto situaci lze dobře ilustrovat na následujícím příkladu prázdného prostoru o rozměrech 15 m × 28 m × 7 m (typické rozměry tělocvičny). Uvažovány jsou dvě varianty – bez podhledu a se zvukově pohltivým podhledem s hodnotou α = 0,9 (v oktávových kmitočtových pásmech 250 Hz až 4 000 Hz). Ostatní povrchy mají činitel zvukové pohltivosti α = 0,05.
Obr. 3 Křivky poklesu hladiny akustického tlaku pro prostor bez podhledu (vlevo) a se zvukově pohltivým podhledu (vpravo)
Křivky poklesu na obrázku 3 byly stanoveny výpočtem pomocí programu ODEON 10.1. Činitel rozptylovosti vnitřních povrchů byl uvažován ve výši 0,05. Z porovnání obou křivek je zřejmé, že na rozdíl od lineárního poklesu v případě prostoru bez akustických úprav, pokles v prostoru s pohltivým stropem je charakteristický počáteční nelinearitou.
Obr. 4 Doba dozvuku prostoru bez podhledu (vlevo) a se zvukově pohltivým podhledem (vpravo)
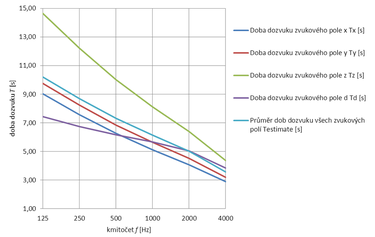
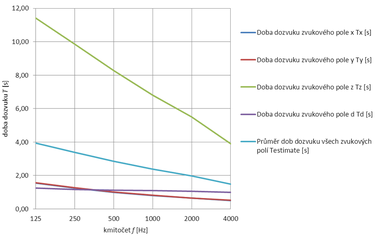
Obr. 5 Doba dozvuku jednotlivých zvukových polí kolmých k osám x, y, z a difuzního pole podle ČSN EN 12354-6, přílohy D pro obě varianty – bez podhledu (vlevo) a se zvukově pohltivým podhledem (vpravo)
Z obrázku 5 je zřejmé, že doba dozvuku zvukového pole z nabývá v prostoru s podhledem znatelně vyšších hodnot než doby dozvuku zvukových polí x a y a difuzního pole. To vede k nárůstu výsledné průměrné doby dozvuku.
![Obr. 6 Schéma hybridní metody podle [11] – TO = transition order (přechod mezi počátečními a pozdními odrazy), ISM = image source method (metoda zdánlivého zdroje), ESR = early scattered rays (metoda počátečních rozptýlených paprsků), RTM = ray-tracing method (metoda trasování paprsku)](/docu/clanky/0094/009450o23.png)
Obr. 6 Schéma hybridní metody podle [11] – TO = transition order (přechod mezi počátečními a pozdními odrazy), ISM = image source method (metoda zdánlivého zdroje), ESR = early scattered rays (metoda počátečních rozptýlených paprsků), RTM = ray-tracing method (metoda trasování paprsku)
Posledním způsobem výpočtu doby dozvuku, zvoleným v rámci této práce, byl software ODEON 10.1, který využívá hybridní metodu výpočtu. Ta se vyznačuje odlišným přístupem k počátečním a pozdním odrazům. Pro počáteční odrazy je použita metoda zdánlivých zdrojů (ISM), které jsou generovány vždy při dopadu zvukových paprsků na odrazivé povrchy. Zvuk šířící se dále ze zdánlivých zdrojů reprezentuje zrcadlové odrazy. Odrazné povrchy jsou navíc považovány za plošné zdroje zvuku vyzařující rozptýlené odrazy (ESR), které přispívají k přenosu počáteční energie. Pro odrazy vyšších řádů je použita speciální metoda trasování parsku (RTM).
3D modelování uzavřených prostorů
Prostorové modely všech prostorů byly vytvořeny pomocí aplikace Google SketchUp a následně převedeny do programu ODEON. Místa zdroje zvuku a příjmu byla rozmístěna ve shodě s polohami reproduktoru a mikrofonu při vlastním měření in-situ. Pro prostory, u nichž byly výsledky měření doby dozvuku převzaty od dodavatele akustických úprav, byly polohy zvoleny náhodně v souladu s ČSN EN ISO 3382-2. Výsledná doba dozvuku představuje prostorový průměr.
Obr. 7 Prostorový model (vlevo) a výpočtový model (vpravo) pro tělocvičnu 8
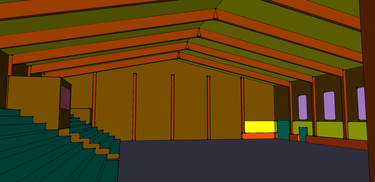
Obr. 8 Reálný stav (vlevo), prostorový model (uprostřed) a výpočtový model (vpravo) pro tělocvičnu 6
Prezentace výsledků
Výsledky měření a výpočtů doby dozvuku jsou pro všechny prostory uvedeny v následující souhrnné tabulce. Doba dozvuku je určena jako průměr z hodnot získaných pro oktávová pásma 500 Hz a 1 000 Hz.
| č. | druh prostoru | Doba dozvuku T [s] | ||||
|---|---|---|---|---|---|---|
| měření | Sabine | Eyring | ČSN EN 12354-6, příloha D | ODEON | ||
| 1 | tělocvična | 4,16 | 3,14 | 3,06 | 3,63 | 3,27 |
| 2 | tělocvična | 1,361) | 1,02 | 0,81 | 1,33 | 1,11 |
| 3 | tělocvična | 1,38 | 1,23 | 1,07 | 1,86 | 1,26 |
| 4 | tělocvična | 2,83 | 1,17 | 0,99 | 2,79 | 2,54 |
| 5 | tělocvična | 1,742) | 1,18 | 0,96 | 1,91 | 1,97 |
| 6 | tělocvična | 4,59 | 4,66 | 4,51 | 5,47 | 5,14 |
| 7 | sportovní hala | 2,64 | 2,72 | 2,66 | 3,04 | 2,58 |
| 8 | sportovní hala | 2,541) | 1,52 | 1,25 | 3,13 | 2,76 |
| 9 | bazénová hala | 2,903) | 2,31 | 2,04 | 2,89 | 2,44 |
| 1) převzato od dodavatele stavebních úprav 2) převzato z publikace [8] 3) převzato z publikace [10] | ||||||
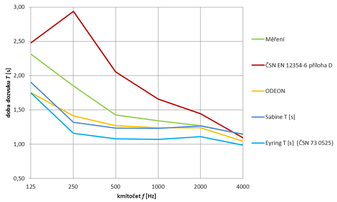
Pro dva vybrané prostory jsou podrobné výsledky v závislosti na kmitočtu prezentovány v následujících grafech a tabulkách.
Obr. 9 Model tělocvičny č. 3 v softwaru ODEON
Obr. 10 Doba dozvuku T tělocvičny č. 3 (T0 = 1,49 s)
| kmitočet f [Hz] | ||||||
|---|---|---|---|---|---|---|
| 125 | 250 | 500 | 1 000 | 2 000 | 4 000 | |
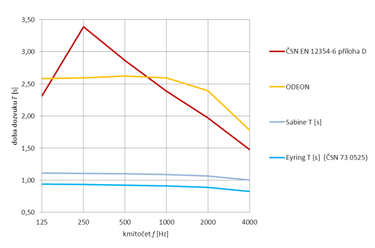
| měření | 2,31 | 1,85 | 1,43 | 1,34 | 1,27 | 1,14 |
| Sabine | 1,90 | 1,32 | 1,23 | 1,23 | 1,27 | 1,14 |
| Eyring | 1,74 | 1,16 | 1,08 | 1,07 | 1,11 | 0,98 |
| ČSN EN 12354-6, příloha D | 2,48 | 2,94 | 2,06 | 1,66 | 1,45 | 1,09 |
| ODEON | 1,75 | 1,41 | 1,27 | 1,24 | 1,24 | 1,04 |
Obr. 11 Model bazénové haly č. 9 v softwaru ODEON
Obr. 12 Doba dozvuku T bazénové haly č. 9 (T0 = 2,28 s)
| kmitočet f [Hz] | ||||||
|---|---|---|---|---|---|---|
| 125 | 250 | 500 | 1 000 | 2 000 | 4 000 | |
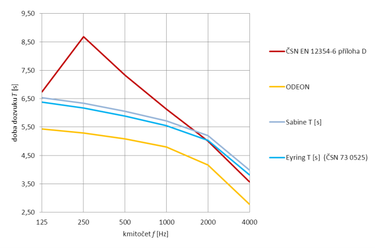
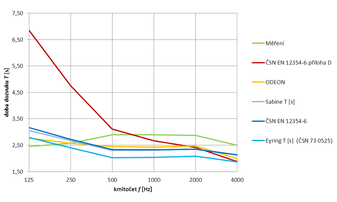
| měření | 2,45 | 2,57 | 2,89 | 2,90 | 2,87 | 2,49 |
| Sabine | 3,06 | 2,68 | 2,30 | 2,31 | 2,36 | 2,14 |
| Eyring | 2,79 | 2,41 | 2,03 | 2,04 | 2,09 | 1,87 |
| ČSN EN 12354-6, příloha D | 6,86 | 4,76 | 3,11 | 2,67 | 2,41 | 1,88 |
| ODEON | 2,77 | 2,57 | 2,45 | 2,43 | 2,47 | 1,99 |
Diskuze výsledků
Hodnocení dosažených výsledků se vztahuje pouze na vybraný soubor devíti staveb, nelze je proto zobecňovat. Lze však předpokládat, že u prostorů obdobného charakteru budou závěry podobné.
Ve vybraných prostorách, kde je pohltivou úpravou opatřen pouze strop (podlaha a stěny jsou odrazivé), se ukazuje změřená doba dozvuku ve všech sledovaných kmitočtových pásmech výrazně delší než výpočtový odhad získaný metodami podle Sabina i Eyringa. Výpočtový postup podle ČSN EN 12354-6, přílohy D poskytuje uspokojivé výsledky pouze pro střední a vyšší kmitočty. Pro nižší kmitočty je vypočtená doba dozvuku obvykle příliš dlouhá. Nejlepšího odhadu je dosaženo výpočtem pomocí softwaru ODEON, který se nejlépe shoduje s výsledky měření v celém kmitočtovém rozsahu.
Rozdíl mezi dobou dozvuku změřenou a vypočtenou metodami podle Sabina i Eyringa se sníží při rovnoměrnějším rozložení zvukové pohltivosti v prostoru, například po obkladu stěn. I poté však může být rozdíl významný a metody podle Sabina a Eyringa nemusí vždy poskytovat uspokojivé výsledky.
V prostorách bez pohltivých úprav bývají použitelné všechny metody s výjimkou postupu podle ČSN EN 12354-6, který je určen výhradně pro prostory s nerovnoměrně rozložitelnou pohltivostí nebo pro nepravidelné prostory.
Z výsledků výpočtů dále vyplývá, že pro dosažení optimálních hodnot doby dozvuku u staveb pro sport a tělovýchovu bývá nezbytné provedení akustických úprav nejen na stropě, ale též na stěnách. Nepříznivý vliv nerovnoměrného rozložení pohltivosti na dobu dozvuku lze také částečně zmírnit povrchy, které způsobují rozptýlený odraz zvuku.
Pro odhad doby dozvuku prostorů v rámci vybraného souboru devíti staveb se osvědčil software ODEON. Zbývající metody jsou vhodné pouze ve specifických případech. V další fázi práce budou ověřeny i jiné metody pro výpočet doby dozvuku s nerovnoměrně rozloženou pohltivostí, např. metoda Arau-Puchades (1988) nebo Neubauerova metoda (2001).
Poděkování
Realizace projektu i vznik tohoto článku byly podpořeny grantem č. SGS12/007/OHK1/1T/11 v rámci studentské grantové soutěže ČVUT v Praze pro rok 2012.
Použitá literatura
- [1] ČSN 01 1600 Akustika – Terminologie, 2003
- [2] ČSN 73 0525 Akustika – Projektování v oboru prostorové akustiky – Všeobecné zásady, 1998
- [3] ČSN 73 0527 Akustika – Projektování v oboru prostorové akustiky – Prostory pro kulturní účely – Prostory ve školách – Prostory pro veřejné účely, 2005
- [4] ČSN EN 12354-6 Stavební akustika – Výpočet akustických vlastností budov z vlastností stavebních prvků – Část 6: Zvuková pohltivost v uzavřených prostorech, 2004
- [5] ČSN EN ISO 3382-2 (73 0534) Akustika – Měření parametrů prostorové akustiky – Část 2: Doba dozvuku v běžných prostorech, 2009
- [6] Kaňka, Jan, Stavební fyzika 1: Akustika budov, 2. vyd., Praha: ČVUT, 2007, 120 s., ISBN 978-80-01-03664-8
- [7] Kolmer, Felix; Kyncl, Jaroslav, Prostorová akustika, 1. vyd., Praha: SNTL – Nakladatelství technické literatury, n. p., 1980, 244 s.
- [8] Kupsa, Tomáš, Doba dozvuku v tělocvičně, DEKTIME, 2009, č. 1, s. 16–21
- [9] Tomašovič, Petr; Rychtáriková, Monika et al., Akustika budov: Priestorová akustika, 1. vyd. Bratislava: STU, 2010, 287 s., ISBN 978-80-227-3235-2
- [10] Nováček, Jiří; Prostorová akustika v souvislostech. DEKTIME, 2009, č. 2, s. 4–11
- [11] Christensen, Claus Lynge; ODEON 10.1 User Manual, 2009
This paper deals with predictions of reverberation time of sports buildings in the phase of project preparation. On the set of nine buildings, the comparison of calculated results with in-situ measured data is done. Different prediction methods and computer simulations have been included in this work.
